复杂分布数据的半监督阶段聚类*

张俊溪，吴晓军，蒋江红

1.西安航空学院 车辆工程学院，西安 710077 2.西北工业大学 自动化学院，西安 710047 3.陕西师范大学 计算机科学学院，西安 710062

复杂分布数据的半监督阶段聚类*

张俊溪1+，吴晓军2，蒋江红3

1.西安航空学院 车辆工程学院，西安 710077 2.西北工业大学 自动化学院，西安 710047 3.陕西师范大学 计算机科学学院，西安 710062

ZHANG Junxi,WU Xiaojun,JIANG Jianghong.Semi-supervised clustering algorithm for complex distributed data.Journal of Frontiers of Computer Science and Technology,2016,10(7)：1003-1009.

半监督聚类是一种用先验信息完善聚类过程的机器学习方法。通过将元胞自动机（cellular automata，CA）距离变换算法引入到半监督聚类过程中，采用平面距离变换算法将数据集划分为若干子类，获得聚类数和约束信息，并作为下一阶段聚类的先验信息。利用半监督K-means聚类算法对第一阶段的聚类结果做进一步划分，可以获得完整的聚类中心和聚类数，并由此提出CA-K-means二阶段聚类算法。采用3组人工数据集和3组标准UCI数据集进行对比仿真实验，将CA-K-means二阶段聚类算法与半监督K-means聚类算法、遗传K-means聚类算法和单纯的CA层次聚类算法进行对比，结果显示，该算法对复杂分布数据的聚类准确率较高，聚类性能更加优良。

元胞自动机；半监督聚类；K-means聚类算法；CA-K-means二阶段聚类；复杂分布

1　引言

聚类是数据挖掘领域最重要的技术之一，也是一种重要的数据分析方法。目前已经应用到模式识别、机器学习及图像处理等多个领域[1]。聚类的任务是通过相似性度量矩阵找到样本之间的相似程度，使得类内的相似度最大，类间的相似度最小，是一种典型的无监督聚类。半监督聚类则是通过将部分先验知识加入到无监督聚类过程中以改善聚类特性[2-3]。由于半监督聚类结合了无监督聚类和监督聚类的特点，近年来在各个领域也成为研究热点[4-5]。Basu等人提出一个基于K-means的半监督算法，将约束信息和距离信息引入作为监督信息[6]；Xing等人通过定义两个样本之间的距离，并构造优化函数，求解度量矩阵使得类内的样本点距离较近，类间的样本点距离较远[7]；高莹等人提出一种半监督K-means多关系数据聚类算法，在K-means聚类算法的基础上扩展了初始聚类中心的选择方法及相似性度量方法[8]；李岩波等人提出一种人工免疫半监督聚类，采用流行距离度量样本间距，采用克隆选择算法求得最优类心[9]。对半监督聚类改进的共同特点是加入不同的约束信息使得监督信息更加完善，以此提高聚类的效率，而K-means算法本身仅适用于凸状数据的聚类，对于复杂的非凸数据集聚类效果较差，因此对于半监督聚类的改进需要更多地关注数据集的多样性和算法的泛化性。

传统的半监督聚类多针对常规数据集的分析，通过增加先验知识提高收敛效率和收敛精度，但针对复杂分布数据的半监督聚类仍需进一步研究。复杂分布数据往往表现为复杂的非凸特性，需要注重其聚类形状及空间、属性的邻接性以及数据分布密度等特性，传统的聚类算法难以得出满意的结果。为了提高聚类结果的准确率和效率，数据之间的关联特性以及数据的多关系特性都需要进行有效的处理，或者通过多阶段聚类[10]以得到满意的聚类结果。本文针对复杂分布数据的特性，提出将元胞自动机距离变换算法应用于聚类过程，并将其得到的类别数和约束信息作为半监督K-means聚类算法的先验知识，通过半监督K-means聚类对结果做进一步划分，得到新的聚类中心。最后通过3组人工数据集和3组标准UCI数据集，分别从聚类性能和准确度两个方面验证了算法的性能。

2　元胞自动机距离变换算法

元胞自动机（cellular automata，CA），也称细胞自动机，是一种时间、空间和状态都离散，可用于模拟复杂系统时空演化过程的动力学模型[11]。采用元胞自动机距离变换算法模拟聚类过程可将元胞自动机描述为一个四元组A=(Ld,S,N,f)，其中Ld表示待聚类对象的维度是d时对应的网格空间；S表示待聚类对象中元胞在变换过程中的状态；N表示待聚类对象的所有数据点（包含聚类中心点），即包含有n个不同元胞状态的空间向量；f则表示中心元胞与邻居元胞间的转换规则，即按照预定的目标函数进行转换的模型[11]。

CA模型由Von Neumann于20世纪中叶[12]提出,具有与传统数学模型截然不同的建模思路，可以模拟生态、环境、自然灾害等多种高度复杂的地理现象，具有模拟非线性复杂系统的突现、混沌、进化等特征，在地理研究领域取得了丰硕的研究成果。元胞自动机在栅格空间上的距离变换是一种空间扩散运动，其距离分为外距离变换、内距离变换和条件距离变换3种[13]。邻居分为多种类型，常见的有一维邻居、冯诺依曼邻居和摩尔邻居等。鉴于本文采用CA进行层次聚类时采用的为自下而上合并聚类，而摩尔邻居能够涵盖聚类对象的全部邻居信息，故本文采用摩尔邻居。元胞自动机应用于聚类的研究已有学者进行了有效的尝试[14-15]，元胞自动机并行计算以及易于向高维空间扩散的性能也成为其应用于聚类的极大优势。

本文采用的摩尔邻居将元胞的状态定义为3种：原状态、扩展状态和空状态。以待聚类对象的约束规则作为目标函数在离散的演化周期上进行扩散，一个周期后原状态元胞经过扩展后如图1所示。

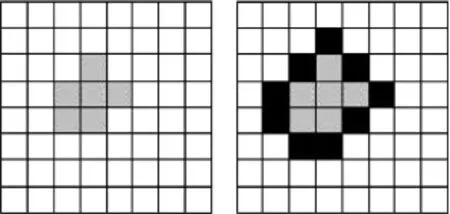
Fig.1　Clustering result after one cycle图1　一个周期后生成的聚类效果

3　CA-K-means二阶段聚类

3.1CA层次聚类

假设聚类对象分布于w×h的d维栅格空间，w为空间的横向长度，h为纵向长度，以二维空间为例，构造元胞自动机 A=(Ld,S,N,f)，其中元胞空间L={ci,j|0≤i≤w,0≤j≤h}，采用状态为空的定值边界[16]，Moore邻居，设共有n个栅格，即n=w×h，则邻居定义如式（1）：

其中，vix、viy表示邻居元胞的行列坐标值；vox、voy表示中心元胞的行列坐标值，对于Moore型邻居来说，维数为d时，邻居个数为3d-1。

元胞状态定义为：

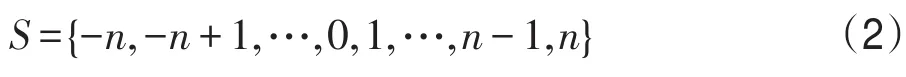
其中，以S=0标记为元胞的空状态；S>0标记为元胞的源状态，其状态记录了当前元胞的索引；S<0标记为扩展状态，其绝对值表明了扩展到该位置的源元胞索引，如式（3）所示：

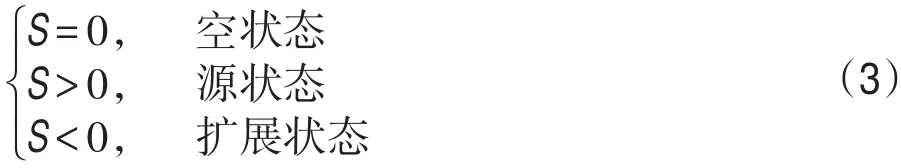
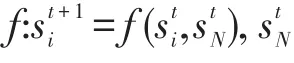
元胞自动机根据以上规则进行演化，直到所有元胞合并为一个簇。

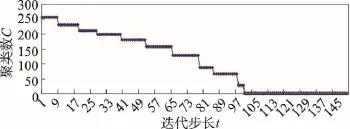
规则中元胞自动机的层次聚类情况如图2（a）所示，原始对象为526个，初始状态，，在时间和空间上进行演化迭代，迭代步长为t，经过98步，元胞状态从初始状态演化为，且，中心元胞和邻居元胞状态都不再发生改变，迭代过程如图3所示。

待聚类对象从C=526经过98步演化为C=2，并且在相当长一段时间内不再发生变化，在t=98～ 150演化周期内C均未发生改变，表明C=2即为该样本的最佳聚类簇。将两类数据C1和C2作为标记数据，为第二阶段聚类提供先验信息。

Fig.2　State evolution of CA图2　元胞自动机状态演化示意图

3.2K-means划分聚类

经过第一阶段的层次聚类后，获得了基本先验知识，将成对约束先验信息加入到K-means聚类过程中。成对约束信息表述为样本点之间的相似性，规定样本之间为强相似性must-link和强差异性connotlink[18]。算法步骤如下：

（1）选择C1和C2两个簇中的任意两个对象xo1和xo2作为初始聚类中心，并将这个初始聚类中心视为所在类别的所有样本。

初始中心的计算：

其中，规定样本个数为n，聚类簇为k,i=0,1,…,n,j=1,2,…,k。

（2）根据样本的成对约束信息，以及每个聚类对象的均值计算这些对象与聚类中心的距离，并根据目标函数进行划分。

目标函数仍然使用K-means算法的距离最短原则：

（3）计算目标函数，当满足收敛条件时算法终止，否则转第（2）步。

3.3算法复杂度分析

单纯的合并层次聚类算法复杂度为O(N)，其中N为待聚类对象个数。单纯的K-means算法复杂度为O(NKT)，其中N为待聚类对象个数，K为聚类类别数，T为迭代时间。将两者合并为二阶段聚类，那么算法复杂度有所增加，会达到O(N2KT)。对整体算法的时间复杂度来讲，影响因素主要在于待聚类对象的规模以及进行二阶段运算，由于二阶段运算耗费时间，并且第二阶段需要第一阶段的先验知识作为监督信息，故运算过程略有复杂化。

4　仿真实验与结果对比

为了验证算法的可行性，分别选用3组具有典型结构和分布特征的人工数据集和3组标准UCI数据集进行实验，所有计算均在PC机上采用Visio Studio 6.0编译环境，使用C语言编程实现。聚类结果通过图形的方式显示，并将聚类结果的准确率（correct rate，CR）作为评价算法有效性的主要指标。准确率CR定义为：

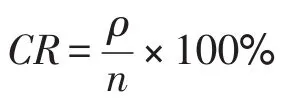
其中，ρ为正确聚类的对象个数；n为待聚类对象总数。

4.1人工数据集实验结果

通过3组具有典型分布特征的人工数据集分析，分别采用半监督K-means聚类算法和本文提出的CA-K-means聚类算法进行运算比较，聚类结果如图4所示。

图4中相同颜色的样本点被分为同一类中，人工数据集1为凸状数据集，聚类结果较为理想，准确率CR约为95%，人工数据集2和3为非凸状数据集，数据集2聚类的准确率CR约为50%，数据集3聚类的准确率约为30%。然后用本文提出的CA-K-means算法进行聚类，3组人工数据集的聚类结果如图5所示，聚类的准确率CR均为100%。

K-means算法本身是基于划分的聚类方法，对于非凸数据集聚类准确率低，且无法事先确定聚类数。本文提出的CA-K-means聚类算法能够很好地解决非凸数据集的聚类问题，并能够提供聚类数和类别的成对约束信息，通过二阶段聚类较好地解决了数据集形状的局限，同时聚类结果准确率较高。

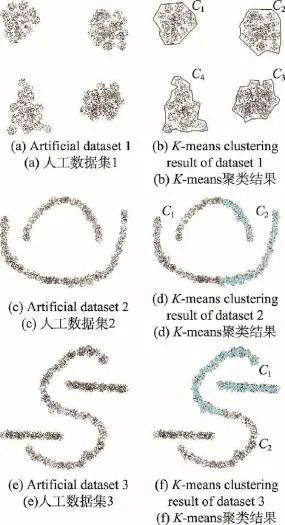
Fig.4　Artificial datasets and K-means clustering results图4　人工数据集及其K-means聚类结果

Fig.5　Clustering results of 3 artificial datasets by CA-K-means图5　3组人工数据集经过CA-K-means算法聚类结果

4.2UCI数据集实验结果

为了验证算法的泛化性能，同时选取了3组标准UCI数据集进行相同的仿真实验，具体数据集信息如表1所示。

分别采用K-means算法、遗传K-means聚类算法、单纯CA层次聚类算法和CA-K-means聚类算法进行运算比较，以本文定义的聚类准确率CR作为评判标准，得到3组UCI数据集的聚类准确率比较如表2所示。

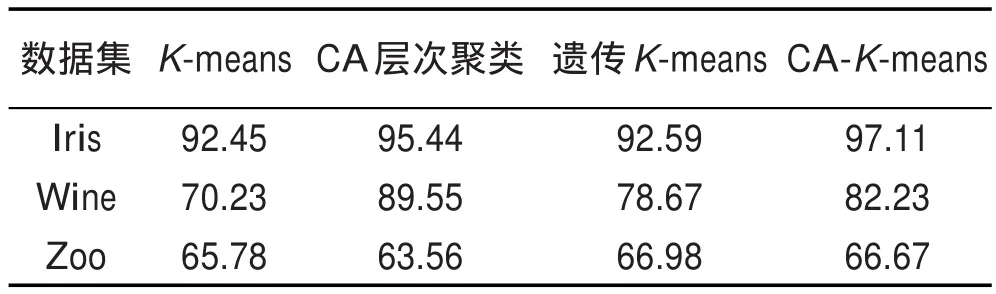
Table 2　Comparison of CR for 3 UCI datasets表2　3组UCI数据集CR比较　%

由表2可以看出，单纯K-means算法对3组数据集的聚类算法准确率均低于CA层次聚类和CA-K-means聚类，而CA层次聚类对Iris和Zoo的聚类准确率均低于CA-K-means聚类。

为了更充分地说明CA-K-means二阶段聚类的优越特性，本文将3组UCI数据Iris、Wine和Zoo的聚类过程收敛特性进行了对比分析，分别采用半监督K-means聚类算法、遗传K-means聚类算法、单纯的CA聚类算法以及CA-K-means聚类算法进行聚类，采用3.2节定义的适应度函数值作为目标函数，3组曲线图如图6所示，横坐标为迭代步数，纵坐标为适应度函数值。从3组收敛特性曲线可以看出，CA-K-means对3组数据的收敛效率均为最优，遗传K-means优于半监督K-means聚类算法，而CA聚类的收敛特性则介于遗传K-means和半监督K-means之间。这是因为遗传K-means采用全局搜索，可以一定程度克服单纯K-means容易获得局部最优解的缺点。单纯的CA聚类可以得出最终的聚类结果，但是收敛效率较低，计算复杂度高。

因此本文提出的元胞自动机距离变换与半监督K-means算法相结合的二阶段聚类算法性能较为优良，聚类准确率高，收敛效率高，适用范围较广，对复杂分布数据的聚类效果尤其明显。

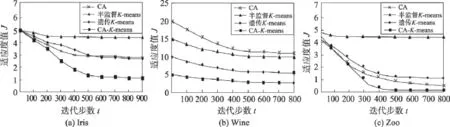
Fig.6　Convergence curves of 3 UCI datasets图6　3组UCI数据集的算法收敛特性对比图

5　结论

本文通过引入元胞自动机距离变换算法，将CA层次聚类结果作为先验信息为半监督K-means聚类算法提供约束信息，提出了一种基于约束和距离融合的半监督聚类算法——CA-K-means聚类算法。该算法分为两个阶段，第一阶段用CA层次聚类获得类别数和簇的标记信息，并将其作为第二阶段聚类的先验信息，通过在K-means聚类过程中加入约束信息得到了完整的聚类结果。最后通过多组具有不同分布特征的数据集聚类实验，验证了本文算法聚类准确率较高，尤其针对复杂分布数据聚类性能较好。

但是本文算法仍然有不足之处和需要改进的地方，如二阶段聚类的时间复杂度问题及半监督聚类的约束信息简化问题等。分阶段聚类往往导致增加时间复杂度来优化聚类性能，同时约束信息过多导致聚类问题变成有监督分类，达不到预期效果，这些都是需要进一步研究的问题。

[1]Yuan Liyong,Wang Jiyi.An improved semi-supervised K-means clustering algorithm[J].Computer Engineering and Science,2011,33(6):138-143.

[2]Li Kunlun,Cao Zheng,Cao Liping,et al.Some developments on semi-supervised clustering[J].Pattern Recognition andArtificial Intelligence,2009,22(5):735-742.

[3]Zhao Weizhong,Ma Huifang,Li Zhiqing,et al.Efficiently active learning for semi-supervised document clustering[J]. Journal of Software,2015,23(6):1486-1497.

[4]Yin Xuesong,Hu Enliang,Chen Songcan.Discriminative semi-supervised clustering analysis with pairwise constraints [J].Journal of Software,2008,19(11):2791-2802.

[5]Tao Xinmin,Xu Jing,Yang Libiao.Improved cluster algorithm based on K-means and particle swarm optimization[J]. Journal of Electronics&Information Technology,2010,32 (1):92-97.

[6]Bilenko M,Basu S,Mooney R J.Integrating constraints and metric learning in semi-supervised clustering[C]//Proceedings of the 21st International Conference on Machine Learning, Banff,Canada,Jul 2004.New York,USA:ACM,2004:81-88.

[7]Xing E P,Ng A Y,Jordan M.Distance metric learning,with application to clustering with side information[C]//Proceedings of the 16th Annual Conference on Neural Information Processing Systems,Vancouver,Canada,Dec 8-13,2003.Cambridge,USA:MIT Press,2003:505-512.

[8]Gao Ying,Liu Dayou,Qi Hong,et al.Semi-supervised K-means clustering algorithm for multi-type relational data[J]. Journal of Software,2008,19(11):2814-2821.

[9]Li Yanbo,Song Qiong,Guo Xinchen.Artificial immune clustering semi-supervised algorithm based on manifold distance[J].Computer Science,2012,39(11):204-207.

[10]Gong Maoguo,Wang Shuang,Ma Meng,et al.Two-phase clustering algorithm for complex distributed data[J].Journal of Software,2011,22(11):2760-2770.

[11]Chen Shupeng.Urbanization and urban geographic information system[M].Beijing:Science Press,1999:171-197.

[12]Von Neumann J.Theory of self-reproducing automata[M]. Illinois,USA:University of Illinois Press,1966.

[13]Wen Kai.Research on evolution and computation with cellular automata[D].Nanjing:Nanjing University of Aeronautics andAstronautics,2008:6-12.

[14]Zhang Junxi,Xue Huifeng,Su Jinqi.Agglomerative clusteringalgorithm based on CA[J].Computer Engineering and Applications,2008,44(23):151-153.

[15]Liu Yong,Xu Qiuyan,Wang Honggang,et al.Intelligent optimizations algorithm for clustering analysis[J].Computer Engineering andApplications,2009,45(19):123-124.

[16]Zhou Chenghu,Sun Zhanli,Xie Yichun.Study of geographical elements of automaton[M].Beijing:Science Press,2001:23-36.

[17]Conway J.Game of life[J].Scientific American,1970,223: 120-123.

[18]Zhang Zhen,Wang Binqiang,Yi Peng.Semi-supervised affinity propagation clustering algorithm based on stratified combination[J].Journal of Electronics&Information Technology,2013,35(3):645-651.

附中文参考文献：

[1]袁利永,王基一.一种改进的半监督K-means聚类算法[J].计算机工程与科学,2011,33(6):138-143.

[2]李昆仑,曹铮,曹丽苹,等.半监督聚类的若干新进展[J].模式识别与人工智能,2009,22(5):735-742.

[3]赵卫中,马慧芳,李志清,等.一种结合主动学习的半监督文档聚类算法[J].软件学报,2015,23(6):1486-1497.

[4]尹学松,胡恩良,陈松灿.基于成对约束的判别型半监督聚类分析[J].软件学报,2008,19(11):2791-2802.

[5]陶新民,徐晶,杨立标.一种改进的粒子群和K均值混合聚类算法[J].电子与信息学报,2010,32(1):92-97.

[8]高莹,刘大有,齐红,等.一种半监督K均值多关系数据聚类算法[J].软件学报,2008,19(11):2814-2821.

[9]李岩波,宋琼,郭新辰.基于流形距离的人工免疫半监督聚类算法[J].计算机科学,2012,39(11):204-207.

[10]公茂果,王爽,马萌,等.复杂分布数据的二阶段聚类算法[J].软件学报,2011,22(11):2760-2770.

[11]陈述彭.城市化与城市地理信息系统[M].北京:科学出版社,1999:171-197.

[13]闻凯.元胞自动机的进化与计算研究[D].南京:南京航空航天大学,2008:6-12.

[14]张俊溪,薛惠锋,苏锦旗.基于CA模型的凝固聚类算法[J].计算机工程与应用,2008,44(23):151-153.

[15]刘勇,许秋艳,王洪刚,等.智能优化算法在聚类分析中的应用[J].计算机工程与应用,2009,45(19):123-124.

[16]周成虎,孙战利,谢一春.地理元胞自动机研究[M].北京:科学出版社,2001:23-36.

[18]张震,汪斌强,伊鹏.一种分层组合的半监督近邻传播聚类算法[J].电子与信息学,2013,35(3):645-651.

ZHANG Junxi was born in 1983.She received the M.S.degree in automation from Northwestern Polytechnical University in 2009.Now she is a lecturer at XiƳan Aeronautical University.Her research interests include pattern recognition and artificial intelligence,etc.

张俊溪（1983—），女，河南新乡人，2009年于西北工业大学获得硕士学位，现为西安航空学院讲师，主要研究领域为模式识别，人工智能等。

WU Xiaojun was born in 1970.He received the Ph.D.degree in automation from Northwestern Polytechnical University.Now he is a professor and Ph.D.supervisor at Northwestern Polytechnical University and Shaanxi Normal University,and the senior member of CCF.His research interests include machine learning and complex system,etc.

吴晓军（1970—），男，陕西凤翔人，博士，西北工业大学、陕西师范大学教授、博士生导师，CCF高级会员，主要研究领域为机器学习，复杂系统等。

JIANG Jianghong was born in 1990.He is an M.S candidate at Shaanxi Normal University.His research interests include machine learning and data mining,etc.

蒋江红（1990—），陕西师范大学计算机科学学院硕士研究生，主要研究领域为机器学习，数据挖掘等。

Semi-supervised ClusteringAlgorithm for Complex Distributed Dataƽ

ZHANG Junxi1+,WU Xiaojun2,JIANG Jianghong3
1.College of Vehicle Engineering,Xi’anAeronautical University,Xi’an 710077,China 2.College ofAutomation,Northwestern Polytechnical University,Xi’an 710047,China 3.School of Computer Science,Shaanxi Normal University,Xi’an 710062,China +Corresponding author:E-mail:zhang_junxi@126.com

Semi-supervised clustering algorithm is a machine learning method which uses the priori information to improve the clustering process.Cellular automata(CA)distance transform algorithm is induced into the process of semi-supervised clustering.The dataset is divided into several clusters by distance transform of cellular automata, and then the number of clusters and the constraint information are obtained,which can be used as priori information of the next phase of clustering.In the second phase of clustering,the semi-supervised K-means clustering algorithm is used to further divide the results of the first phase and the final clustering results are got.Based on that,this paper proposes the CA-K-means clustering algorithm.By comparing the proposed algorithm with K-means algorithm,GAK-means and pure CA clustering algorithm,the experimental results on three artificial data sets and three UCI data sets with different structures show that the novel algorithm has higher clustering accuracy for complex distributed data and more optimal clustering feature.

cellular automata;semi-supervised clustering algorithm;K-means clustering algorithm;CA-K-meanstwo phases clustering algorithm;complex distribution

2015-07,Accepted 2015-10.

10.3778/j.issn.1673-9418.1507102

A

TP181

*The Natural Science Foundation of Shaanxi Province under Grant No.2014JM8353(陕西省自然科学基金).

CNKI网络优先出版:2015-10-28,http://www.cnki.net/kcms/detail/11.5602.TP.20151028.1045.004.html