Normality Criteria of Meromorphic Functions
2016-10-12WangQiongYuanWenjunChenWeiandTianHonggen
Wang Qiong,Yuan Wen-jun,Chen Weiand Tian Hong-gen,*
(1.School of Mathematics Science,Xinjiang Normal University,Urumqi,830054)
(2.School of Mathematics and Information Sciences,Guangzhou University, Guangzhou,510006)
(3.School of Mathematics Sciences,Shandong University,Jinan,250000)
Communicated by Ji You-qing
Normality Criteria of Meromorphic Functions
Wang Qiong1,Yuan Wen-jun2,Chen Wei3and Tian Hong-gen1,*
(1.School of Mathematics Science,Xinjiang Normal University,Urumqi,830054)
(2.School of Mathematics and Information Sciences,Guangzhou University, Guangzhou,510006)
(3.School of Mathematics Sciences,Shandong University,Jinan,250000)
Communicated by Ji You-qing
In this paper,we consider normality criteria for a family of meromorphic functions concerning shared values.Let F be a family of meromorphic functions defined in a domain D,m,n,k and d be four positive integers satisfying m≥n+2 andand a(≠0),b be two finite constants.Suppose that every f∈F has all its zeros and poles of multiplicity at least k and d,respectively.If(fn)(k)−afmand(gn)(k)−agmshare the value b for every pair of functions(f,g)of F,then F is normal in D.Our results improve the related theorems of Schwick(Schwick W. Normality criteria for families of meromorphic function.J.Anal.Math.,1989,52: 241–289),Li and Gu(Li Y T,Gu Y X.On normal families of meromorphic functions. J.Math.Anal.Appl.,2009,354:421–425).
meromorphic function,shared value,normal criterion
2010 MR subject classification:30D30,30D45
Document code:A
Article ID:1674-5647(2016)01-0088-09
10.13447/j.1674-5647.2016.01.07
1 Introduction and Main Results
Let C be the set of complex numbers,D be a domain in C,which means that D is a connected nonempty open subset of C.Let F be a family of meromorphic functions defined in D.For{f,g}⊂F,{a,b}⊂P1=C∪{∞},we write f=a⇒g=b(f=a⇔g=b) if f−1(a)⊂g−1(b)(f−1(a)=g−1(b)),and say that f and g share a ignoring multiplicities(IM,for short)if f−1(a)=g−1(a)(see[1]).Here,the family F is said to be normal in D if any sequence of F must contain a subsequence that locally uniformly spherically converges to a meromorphic function or∞in D(see[2]).
In 1989,Schwick[3]proved a normality criterion:
Theorem 1.1Let k,n(≥k+3)be two positive integers,and F be a family of meromorphic functions defined in a domain D.If(fn)(k)≠1 for every function f∈F,then F is normal in D.
In 1998,Wang and Fang[4]proved:
Theorem 1.2Let k,n(≥ k+1)be two positive integers,and f be a transcendental meromorphic function.Then(fn)(k)assumes every finite non-zero value infinitely often.
For families of meromorphic functions,the connection between normality and shared values has been studied frequently.
By the ideas of shared values,Li and Gu[5]proved the following results:
Theorem 1.3Let F be a family of meromorphic functions defined in a domain D,k, n(≥k+2)be two positive integers,and a≠0 be a finite complex number.If(fn)(k)and (gn)(k)share a in D for every pair of functions f,g∈F,then F is normal in D.
In 2011,Liu and Li[6]studied Theorem 1.3,in which the value a was replaced by the fix-point z,and got the following result:
Theorem 1.4Let F be a family of meromorphic functions defined in a domain D,k, n(≥k+1)be two positive integers.If(fn)(k)and(gn)(k)share z in D for every pair of functions f,g∈F,then F is normal in D.
Lately,some theorems in this area appear.Hu and Meng[7],Jiang and Gao[8]studied the functions of the form f(f(k))n.Ding et al.[9]studied the functions of the form fm(f(k))nand Sun[10]studied the form P(f)(f(k))m.
Naturally,we pose the following question:
QuestionWhether the form(fn)(k)−afmin above Theorems can have similar results?
In this paper,we prove the following theorems and deal with this question.
Theorem 1.5Let F be a family of meromorphic functions defined in a domain D,m, n,k be three positive integers satisfying m≥n+k+3,and a(≠0),b be two finite complex constants.If(fn)(k)−afm≠b for every functions f of F,then F is normal in D.
Whether the condition m≥n+k+3 in Theorem 1.5 can be improved?We get the following results:
Theorem 1.6Let F be a family of meromorphic functions defined in a domain D,m, n,k(≥2)and d be four positive integers satisfying m≥n+k+1 and d≥2,and a(≠0),b be two finite complex constants.Suppose that every f∈F has all its poles of multiplicity at least d and(fn)(k)−afm≠b,then F is normal in D.
By the ideas of shared values,we can get the following results:
Theorem 1.7Let F be a family of meromorphic functions defined in a domain D,m, n,k and d be four positive integers satisfyingand a(≠0),b be two finite constants.Suppose that every f∈F has all its zeros and poles of multiplicity at least k and d,respectively.If(fn)(k)−afmand(gn)(k)−agmshare the value b IM for every pair of functions(f,g)of F,then F is normal in D.
2 Some Lemmas
In order to improve our theorems,we require the following Lemmas.
Lemma 2.1[11]Let F be a family of meromorphic functions on the unit disc∆ such that all zeros of functions in F have multiplicity≥p,and all poles of functions in F have multiplicity≥q.Let α be a real number satisfying−q<α (a)points zj∈∆,zj→z0; (b)functions fj∈F,and (c)positive numbers ρj→0, Lemma 2.2Let f(z)be meromorphic functions such that(fn)(k)(z)≢0,a(≠0)be a finite constant,and m,n,k and d be four positive integers satisfying m≥n+k+1.Then Proof.Set Since(fn)(k)(z)≢0,we know that Ψ(z)≢0. By(2.1),we have Thus,we get which implies that We see that a zero Ψ is attained at pole of f and zeros of(fn)(k)which is not zero of f, and a pole of f must be zero of Ψ by the condition m≥n+k+1.The pole of f cannot be zero of Ψ−1.Hence,if we denote¯N0(r)by the counting function of zeros of both Ψ and (fn)(k),we see that On the other hand,we have So we have Therefore,by(2.3)–(2.7)and Nevanlinna’s first and second fundamental theorems,we have Then,we have the inequality Lemma 2.3Let F be a family of meromorphic functions defined in a domain D,m,n, k and d be four positive integers satisfyingb be two finite complex constants.Suppose that every f∈F has all its zeros and poles of multiplicity at least k and d,respectively,then Proof.By the argument as Lemma 2.2,since the condition that all zeros and poles of f are multiplicities at least k and d,respectively,we get Hence,by(2.9),(2.10)and the inequality(2.8),we get Proof of Theorem 1.5Suppose that F is not normal at z0.Then by Lemma 2.1,there exist fj∈F,zj→z0and ρj→0+such that spherically uniformly on compact subsets of C,where g(ξ)is a nonconstant meromorphic function on C.We have spherically uniformly on compact subsets of C outside poles of g.By hypothesis,(fn)(k)−afm≠b for every functions f of F.Applying Hurwitz theorem,we obtain that or If(gn)(k)−agm≡0,then g has not poles.By the logarithmic derivative lemma,we get Hence and this contradicts with g is nonconstant meromorphic function.Thus, Then(gn)(k)≡0. Indeed,if(gn)(k)≡0,then gnis polynomial with degree at most k−1,which is a contradiction with(gn)(k)−agm≠0.Applying Lemma 2.2 with meromorphic function g, we get This implies By m≥n+k+3,we conclude that g is constant function.This is a contradiction.Hence, F is normal in D. Proof of Theorem 1.6By the argument as Theorem 1.5,we can assume that F is not normal at z0.Then by Lemma 2.1,there exist fj∈F,zj→z0and ρj→0+such that spherically uniformly on compact subsets of C,where g(ξ)is a nonconstant meromorphic function on C and all its poles has multiplicity at least 2.Hence,from the inequality(3.1), we get By hypothesis, we get that g is a constant function.This is a impossible.Hence,F is normal in D. Proof of Theorem 1.7Suppose that F is not normal at z0.Then by Lemma 2.1,there exist fj∈F,zj→z0and ρj→0+such that spherically uniformly on compact subsets of C,where g(ξ)is a nonconstant meromorphic function on C and whose zeros and poles has multiplicity at least k and d,respectively. Moreover,the order of g is at most 2.We have spherically uniformly on compact subsets of C outside poles of g.Hence,we apply Hurwitz theorem and obtain that or If(gn)(k)−agm≡0,since all poles of g have multiplicity at least d,we have Therefore,g is a constant,a contradiction.So By Lemma 2.3,we have Then If(gn)(k)−agm≠0,then(3.2)gives that g is a constant.Hence,(gn)(k)−agmis a meromorphic function and has at least one zero. Next,we prove that(gn)(k)−agmhas just a unique zero. Suppose to the contrary,let ξ0,be two distinct zeros of(gn)(k)(ξ)−agm(ξ),and choose δ>0 small enough such that where By Hurwitz theorem,there exists a sequence of points ξj∈D(ξ0,δ)andsuch that for large enough j, By the assumption that for each pair of functions f,g∈F,(fn)(k)−afmand(gn)(k)−agmshare b in D,we know that for any positive integer m, Hence, Noting that g has zeros and poles of multiplicities at least k and d respectively,then (3.2)deduces that g is a rational function with degree at most 2. If g is a polynomial and noting that degg≤2 and the multiplicities of zeros are at least k,we distinguish two cases. Case 1 degg=1. We can write g=A(ξ−ξ1),where A is a nonzero constant.So Obviously,(gn)′+agmhas at least two distinct zeros,a contradiction. Case 2 degg=2. We distinguish two cases again. Case 2.1 k=1. We can write g=A(ξ−ξ1)(ξ−ξ2),where A is a nonzero constant.Then Obviously,(gn)′+agmhas at least three distinct zeros,a contradiction. Case 2.2 k=2. We can write g=A(ξ−ξ1)2,where A is a nonzero constant.Then Obviously,(gn)′+agmhas at least two distinct zeros,a contradiction. Suppose that g is a rational function with degg≤2 and noting the multiplicities of poles are at leastwe also distinguish two subcases. Subcase 1 degg=1. We can write where A,C are nonzero constants and AD+BC≠0.Then Noting m≥n+2,(gn)′+agmhas at least two distinct zeros,a contradiction. Subcase 2 degg=2. We distinguish three cases. Subcase 2.1 g=0,and g has only one zero. In this case we have where A,A1are two nonzero constants.We conclude that k=2.It follows thata contradiction. Subcase 2.2 g=0,and g has two distinct zeros. In this case we have where A,A1are two nonzero constants.We conclude that k=1 and Furthermore, where A is a nonzero constant.So where degg1<2.Obviously,(gn)′+agmhas at least three distinct zeros,a contradiction. Subcase 2.3 g≠=0. From Lemma 2.3,we get which gives that g is a constant.This is a contradiction. The proof is completed. [1]Schiff J.Normal Families.Berlin:Springer-Verlag,1993. [2]Hayman W K.Meromorphic Functions.Oxford:Clarendon Press,1964. [3]Schwick W.Normality criteria for families of meromorphic function.J.Anal.Math.,1989,52: 241–289. [4]Wang Y F,Fang M L.Picard values and normal families of meromorphic functions with multiple zeros.Acta.Math.Sin.,1998,14(1):17–26. [5]Li Y T,Gu Y X.On normal families of meromorphic functions.J.Math.Anal.Appl.,2009, 354:421–425. [6]Liu Z H,Li Y C.Normal families of meromorphic functions concerning shared fixed-points. Int.Math.Forum.,2011,6(31):1507–1511. [7]Hu P C,Meng D W.Normality criteria of meromorphic functions with multiple zeros.J.Math. Anal.Appl.,2009,357:323–329. [8]Jiang Y B,Gao Z S.Normal families of meromorphic functions sharing a holomorphic fuction and the converese of function Bloch principle.Acta.Math.Sci.,2012,32B(4):1503–1512. [9]Ding J J,Ding L W,Yuan W J.Normal families of meromorphic functions concerning shared values.Complex Var.Elliptic Equ.,2013,58(1):113–121. [10]Sun C X.Normal families and shared values of meromorphic functions.Ann.Math.,2013, 34A(2):205–210. [11]Zalcman L.Normal families:new perspectives.Bull.Am.Math.Soc.,1998,35:215–230. date:Jan.6.2015. The NSF(11461070,11271090)of China,the NSF(S2012010010121,2015A030313346)of Guangdong Province,and the Graduate Research,and Innovation Projects(XJGRI2015106)of Xinjiang Province. . E-mail address:wq1298592600@163.com(Wang Q),tianhg@xjnu.edu.cn(Tian H G).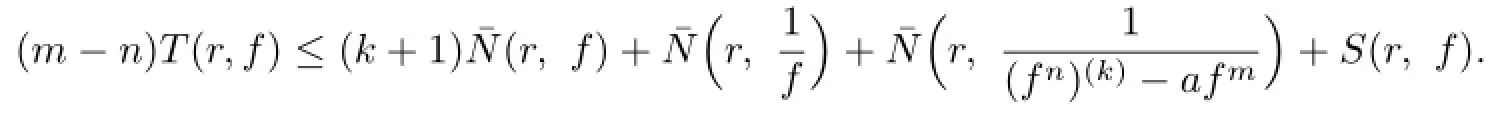


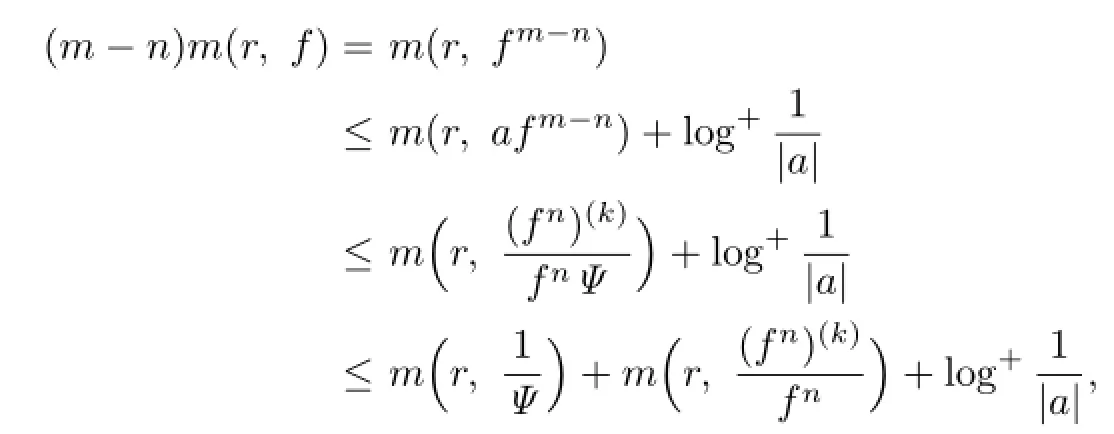


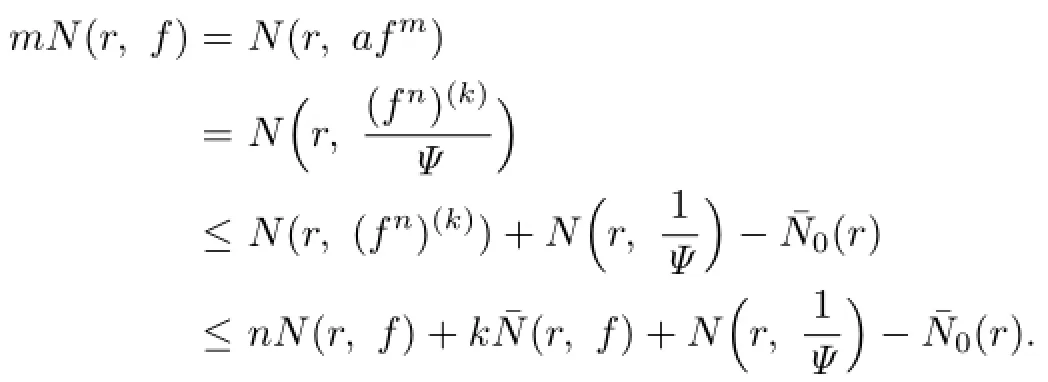
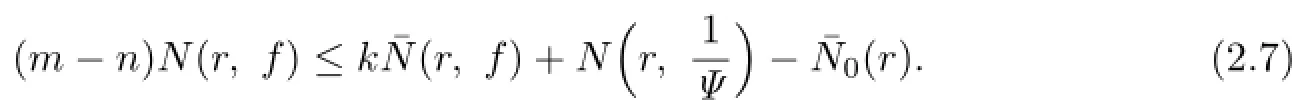
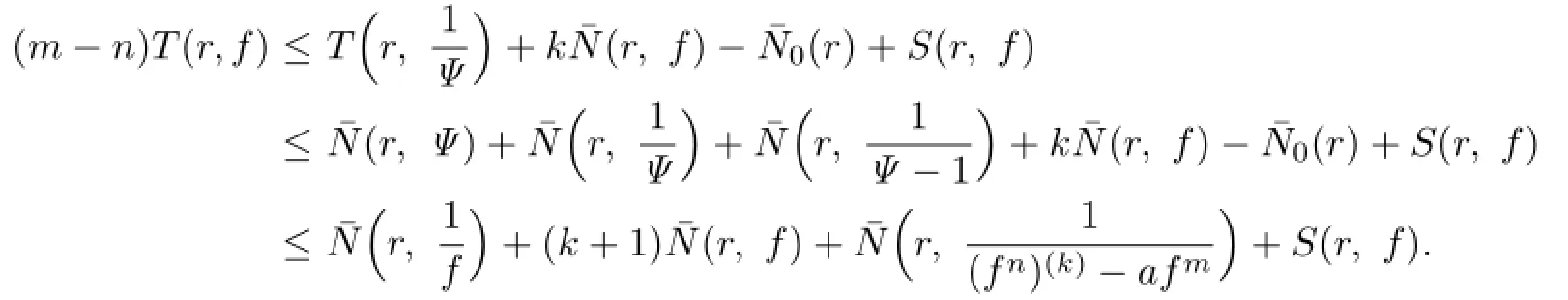

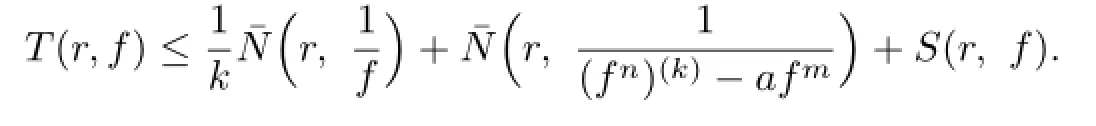
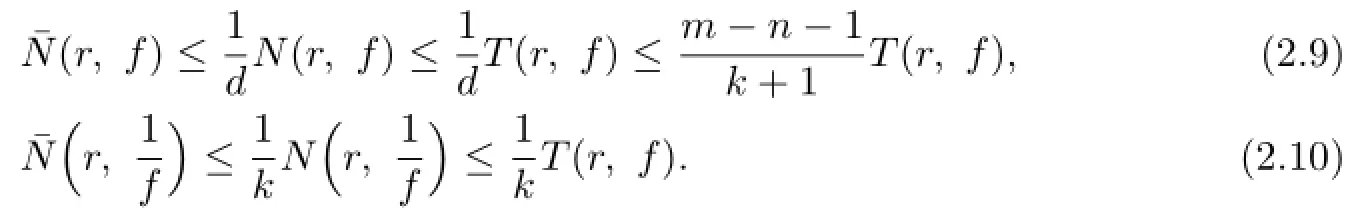
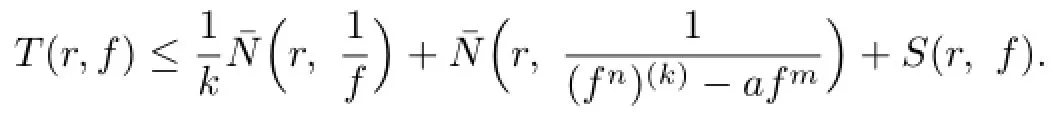
3 Proof of Theorems

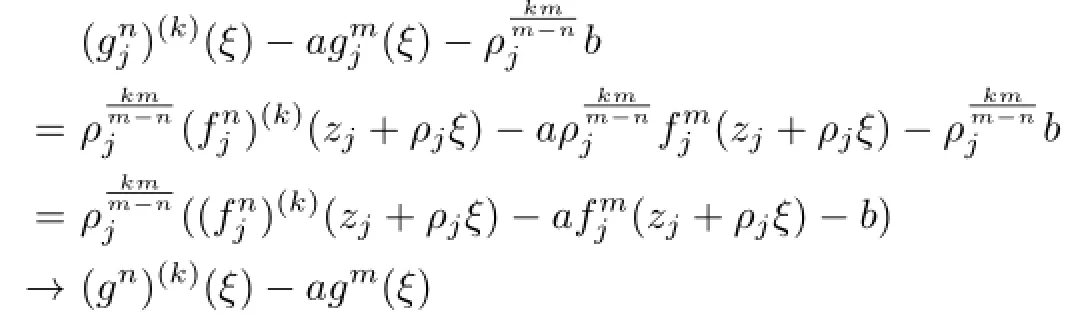
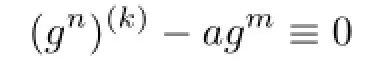

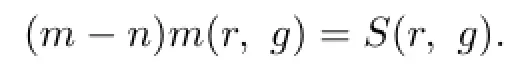
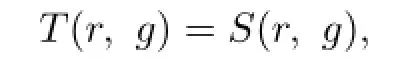
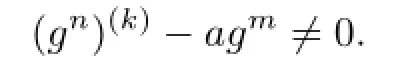
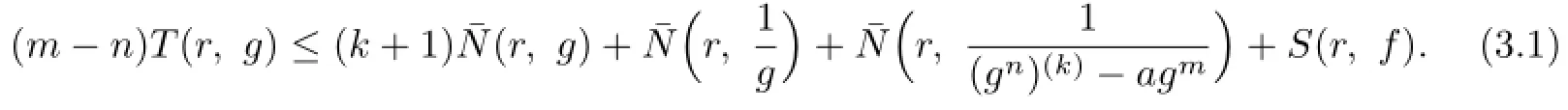

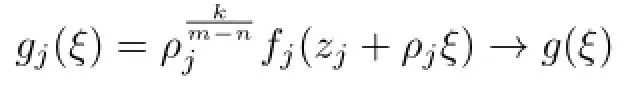
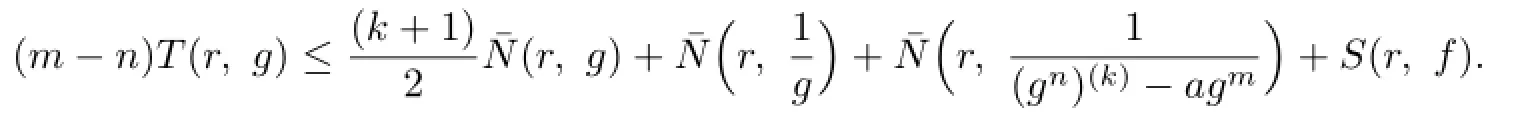
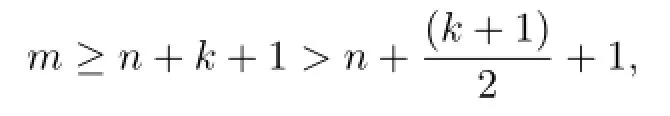

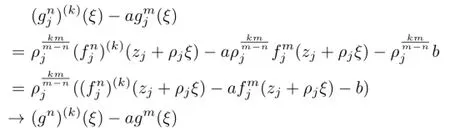
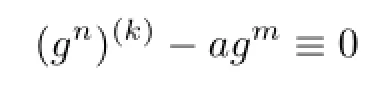
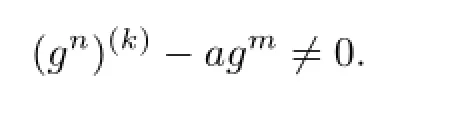

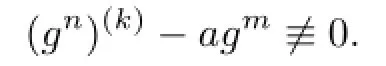
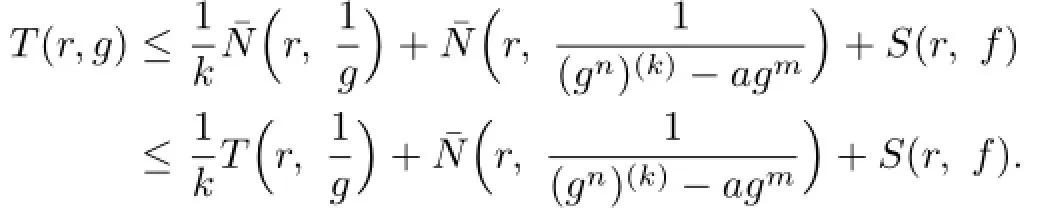
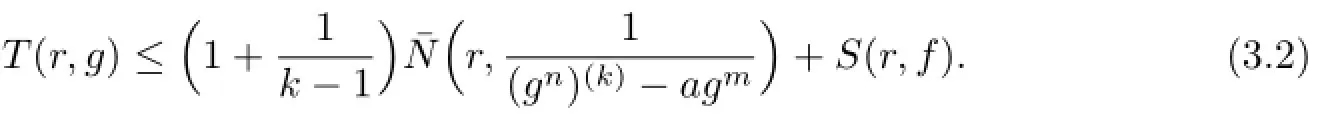
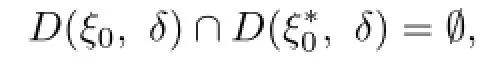

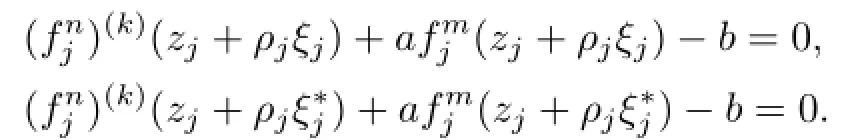
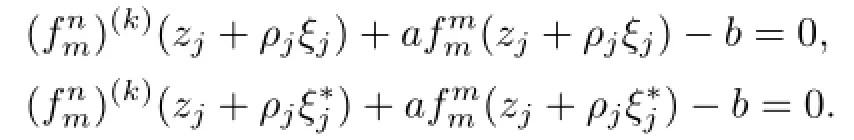
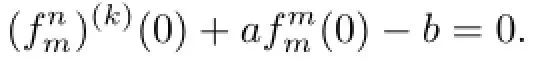

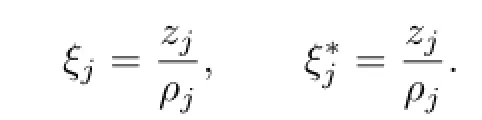
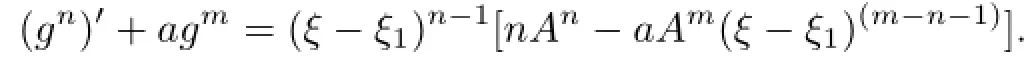


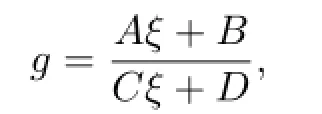
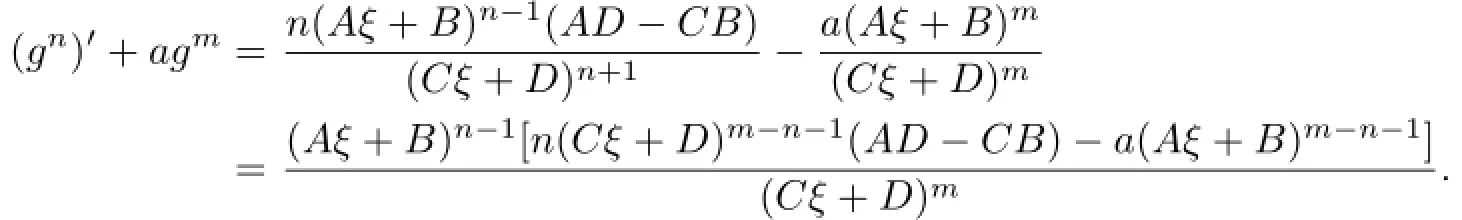

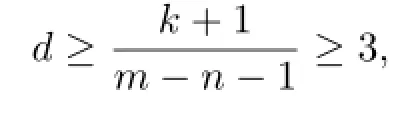
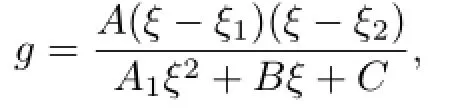
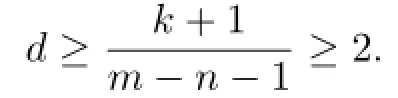

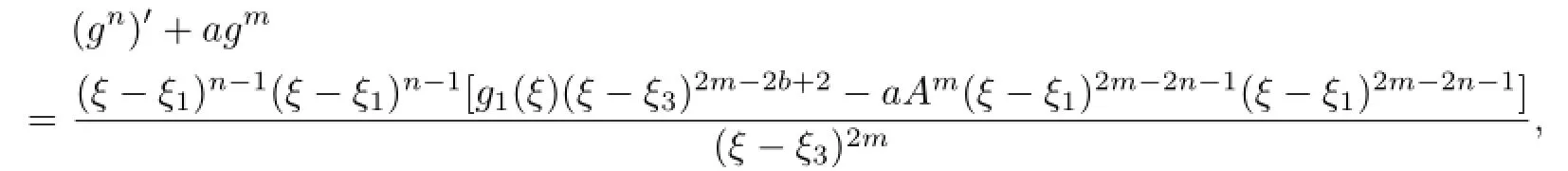
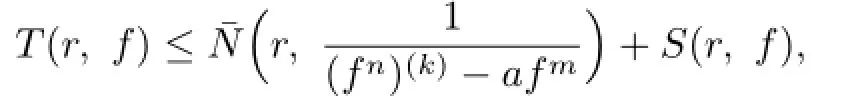
杂志排行
Communications in Mathematical Research的其它文章
- An Identity with Skew Derivations on Lie Ideals
- Ore Extensions over Weakly 2-primal Rings
- L-octo-algebras
- Normality Criteria of Meromorphic Functions Concerning Shared Analytic Function
- A New Generalized FB Complementarity Function for Symmetric Cone Complementarity Problems
- Triple Crossing Numbers of Graphs
