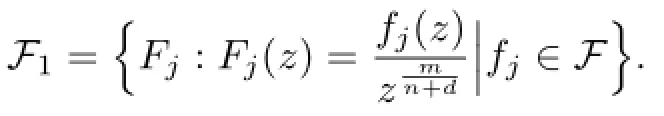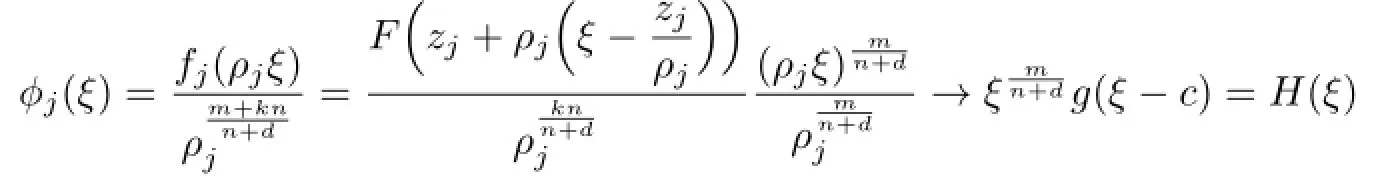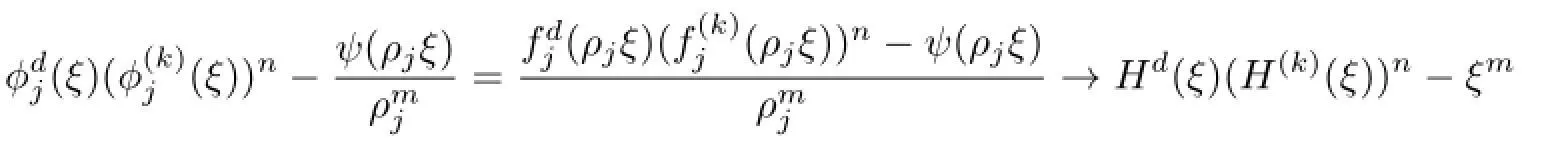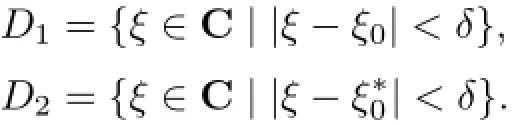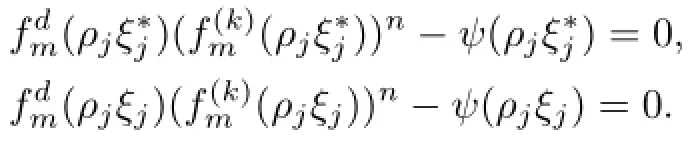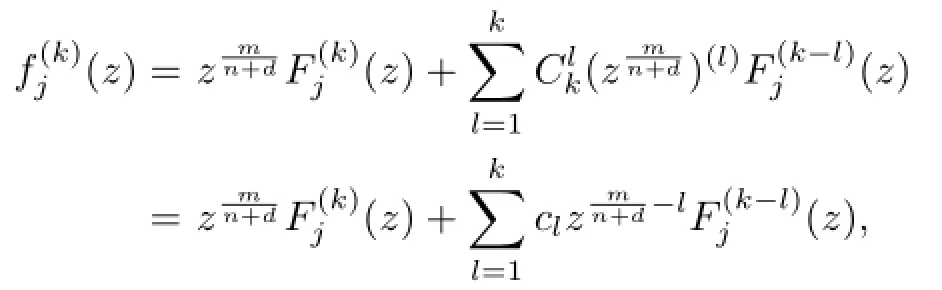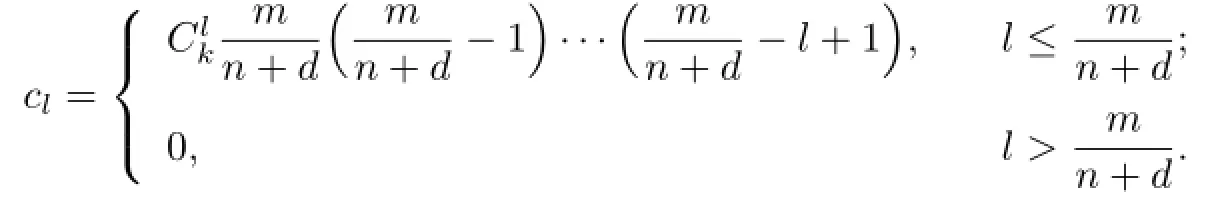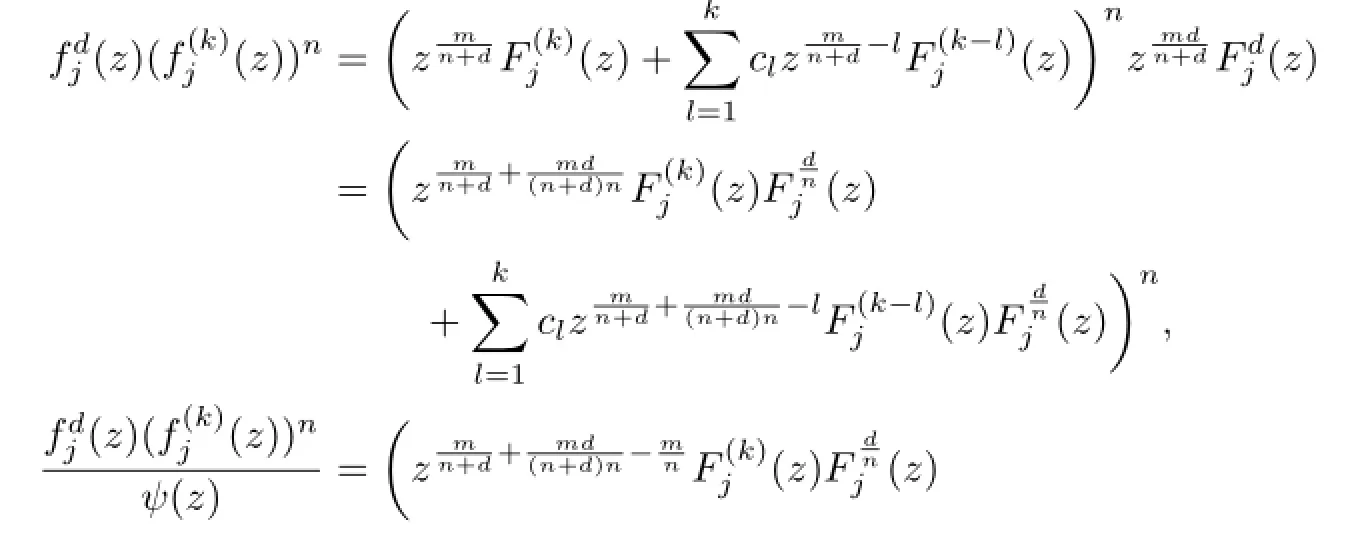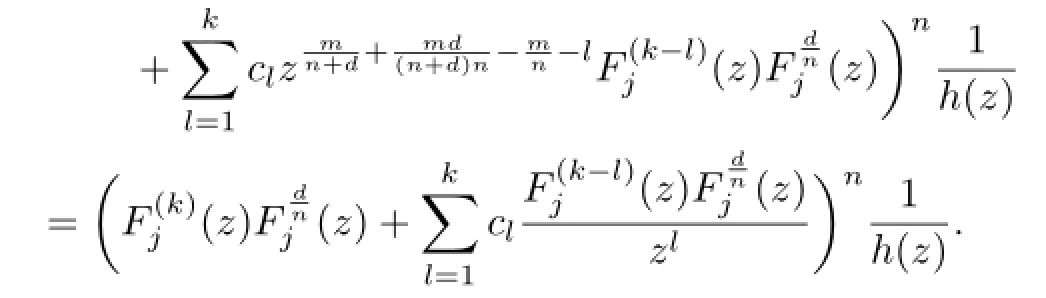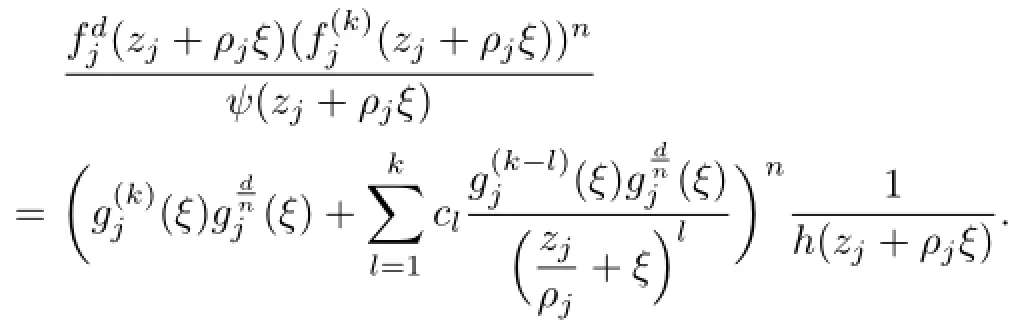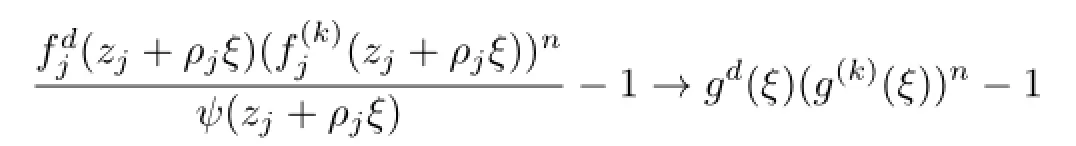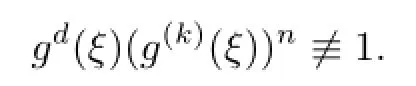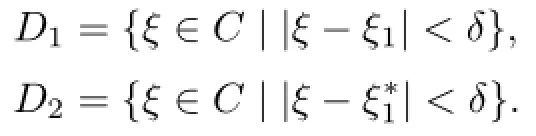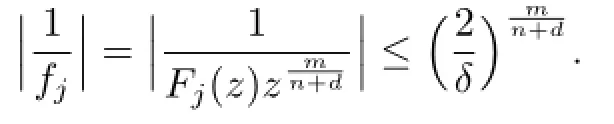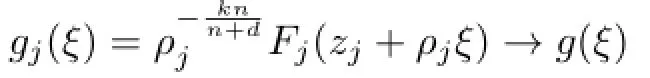Normality Criteria of Meromorphic Functions Concerning Shared Analytic Function
2016-10-12YangQi
Yang Qi
(School of Mathematics Science,Xinjiang Normal University,Urumqi,830054)
Communicated by Ji You-qing
Normality Criteria of Meromorphic Functions Concerning Shared Analytic Function
Yang Qi
(School of Mathematics Science,Xinjiang Normal University,Urumqi,830054)
Communicated by Ji You-qing
In this paper,we use Pang-Zalcman lemma to investigate the normal family of meromorphic functions concerning shared analytic function,which improves some earlier related results.
meromorphic function,entire function,shared function,normal family
2010 MR subject classification:30D35,30D45
Document code:A
Article ID:1674-5647(2016)01-0047-10
10.13447/j.1674-5647.2016.01.03
1 Introduction and Main Results
Let D be a domain in C,and F be a family of meromorphic functions defined in the domain D.F is said to be normal in D if any sequence{fn}⊂F contains a subsequence fnj,which converges spherically locally uniformly in D to a meromorphic function or∞(see[1]–[5]).
Let f(z)be a mermorphic function in a domain D and z0∈D.If f(z0)=z0,we say that z0is the fixed-point of f(z).Let f(z)and g(z)denote two meromorphic functions in D.If f(z)−ψ(z)and g(z)−ψ(z)have the same zeros(or ignoring multiplicity),then we say that f(z)and g(z)share ψ(z)CM(or IM).
In 1998,Wang and Fang[6]proved the following result:
Theorem 1.1Let k and n≥k+1 be two positive integers,and f be a transcendental merimorphic function.Then(fn)(k)assumes every finite nonzero value infinitely often.
Corresponding to Theorem 1.1,there are the following theorems about normal families.
Theorem 1.2[7]Let k and n≥k+3 be two positive integers and F be a family of meromorphic functions defined in a domain D.If(fn)(k)≠1 for every function f∈F,then F is normal in D.
In 2009,Li and Gu[8]proved:
Theorem 1.3Let F be a family of meromorphic functions defined in a domain D.Let k,n≥k+2 be positive integers and a≠0 be a finite complex number.For each pair (f,g)∈F,if(fn)(k)and(gn)(k)share a in D,then F is normal in D.
Lately,many authors studied the functions of the form f(f(k))n.Hu and Meng[9]proved:
Theorem 1.4Take positive integers n and k with n,k≥2,and take a non-zero complex number a.Let F be a family of meromorphic functions in the plane domain D such that each f∈F has all its zeros of multiplicity at least k.For each pair(f,g)∈F,if f(f(k))nand g(g(k))nshare a IM,then F is normal in D.
Recently,Jiang and Gao[10]extended Theorem 1.4 as follows:
Theorem 1.5Let m≥0,n≥2m+2 and k≥2 be three positive integers and m be divisible by n+1.Suppose that a(z)(≢0)is a holomorphic function with zeros of multiplicity m in a domain D.Let F be a family of meromorphic functions in a domain D,and for each f∈F,f has all its zeros of multiplicity max{k+m,2m+2}at least.For each pair (f,g)∈F,if f(f(k))nand g(g(k))nshare a(z)IM,then F is normal in D.
A natural question is:What can be said if the function f(f(k))nin Theorem 1.5 is replaced by the function fd(f(k))n?In this paper,we answer this question by proving the following theorem:
Theorem 1.6Let F be a family of meromorphic functions defined in a domain D,and m≥0,n≥2m+2,k≥2,d≥1,p≥1 be five integers and m be divisible by n+d.Let ψ(z)≢0 be an analytic function with zeros of multiplicity m in a domain D.Suppose that every f∈F has all its zeros of multiplicity at leastFor each pair(f,g)∈F,if fd(f(k))nand gd(g(k))nshare ψ(z)IM,then F is normal in D.
Remark 1.1Obviously,from Theorem 1.6,we can get Theorem 1.5 when d=1.
2 Some Lemmas
In order to prove Theorem 1.6,we require the following results.
Lemma 2.1[11]Let F be a family of meromorphic functions on the unit disc satisfying all zeros of functions in F have multiplicity≥p and all poles of functions in F have multiplicity≥q.Let α be a real number satisfying−q<α a)a number 0 b)points znwith|zn| c)functions fn∈F; d)positive numbers ρn→0 Lemma 2.2Let m≥0,k,n≥2,d≥1 be four integers,H(z)=amzm+am−1zm−1+ ···+a0be a polynomial,where am(≠0),am−1,···,a0are constants.If f is a non-constant polynomial,and the multiplicity of its all zeros is at least,then fd(z)(f(k)(z))n−H(z) has at least two distinct zeros,and fd(z)(f(k)(z))n−H(z)≢0. Proof.Since f is a non-constant polynomial with zeros of multiplicityat least,we know that the degree of f isat least,and Then fd(z)(f(k)(z))n−H(z)has at least one zero. If fd(z)(f(k)(z))n−H(z)has only one zero,we may assume that where λ is a non-zero constant,l is a positive integer.Compare the degrees of H(z)and f(z),we have Then Thus z0is the unique zero of(fd(z)(f(k)(z))n)(m+1).Since f is a non-constant polynomial with zeros of multiplicityat least,we know that z0is a zero of f.Thus it contradicts with Thus,fd(z)(f(k)(z))n−H(z)has at least two distinct zeros. Lemma 2.3Let m ≥0,n≥2m+2,k,d≥1 be four integers,H(z)=amzm+ am−1zm−1+···+a0be a polynomial,where am(≠0),am−1,···,a0are constants.If f is a non-polynomial rational function,and the multiplicity of its all zeros is at least 2m+2, then fd(z)(f(k)(z))n−H(z)has at least two distinct zeros,and fd(z)(f(k)(z))n−H(z)≢0. Proof.Since f is a non-polynomial rational function,it is obvious that Let where A is a non-zero constant,s,t≥1,mi≥2m+2(i=1,2,···,s),nj≥n(k+1)+d (j=1,2,···,t).For simplicity,we denote By differentiating both sides of(2.1)step by step,we have where g1(z)is a non-constant polynomial with deg(g1)≤(m+1)(s+t−1). Now,we discuss two cases. Case 1.If fd(z)(f(k)(z))n−H(z)has a unique zero z0,then we set where B is a non-zero constant and l is a positive integer,P and Q are polynomials with degree M and N,also P and Q have no common factors. Here we discuss two subcases. Subcase 1.1.m≥l. By differentiating both sides of(2.5),we have where g2(z)is a polynomial with deg(g2)≤(m+1)t−(m−l+1).By(2.1)and(2.5),since m≥l,one has From(2.4)and(2.6), Then it contradicts with m≥l. Subcase 1.2.m By differentiating both sides of(2.5),we have where g3(z)is a polynomial with deg(g3)≤(m+1)t. By differentiating both sides of(2.5)step by step for m times,we can get that z0is a zero of(fd(f(k))n)(m)=H(m).Since H(m)=am≠0,one has Here we discuss in two subcases. Subcase 1.2.1.l≠N+m. From(2.1)and(2.5),we obtain deg(P)≥ deg(Q),that is,M ≥N.Since z0≠αi(i=1,2,···,s),(2.4)and(2.7)imply So By using(2.2)and(2.3),we obtain which is a contradiction. Subcase 1.2.2.l=N+m. We further distinguish two subcases. (i)M≥N. By(2.4)and(2.7),we obtain Similar to Subcase 1.2.1,we obtain a contradiction M (ii)M By using(2.4)and(2.7)again,we obtain Hence which is a contradiction. Case 2.If fd(f(k))n−H(z)has no zero,then l=0 in(2.5).Proceeding as in the proof of Case 1,we get a contradiction. Lemma 2.3 is proved. Lemma 2.4[12]Suppose that f(z)is a transcendental meromorphic function,n,k,d are three positive integers.Then,when k≥1,n,d≥2,fd(f(k))n−φ(z)has infinitely many zeros,where φ(z)≢0,T(r,φ)=S(r,f). From Theorem 1.5,when d=1,Theorem 1.6 holds. Next,we prove the case d≥2. For any point z0∈D,either ψ(z0)=0 or ψ(z0)≠0. Case 1.ψ(z0)=0. We may assume z0=0 and ψ(z)=zm+am+1zm+1+···=zmh(z),where am+1,am+2, ···are constants,h(0)=1,and m can be divisible by n+d. Let If F1is not normal at 0,by Lemma 2.1,there exist a sequence{zj}of complex numbers with zj→z0and a sequence{ρj}of positive numbers with ρj→0 such that locally uniformly on compact subsets of C,where g(ξ)is a non-constant meromorphic function in C,all of whose zeros have multiplicity at leastMoreover, g(ξ)has order at most 2. Here we distinguish two cases. locally uniformly on compact subsets of C disjoint from the poles of g,where H(ξ)is a non-constant meromorphic function in C,all of whose zeros have multiplicity at leastMoreover,H(ξ)has order at most 2.So spherically locally uniformly in C disjoint from the poles of g. If Hd(ξ)(H(k)(ξ))n≡ξm,since H has zeros with multiplicity at leastobviously there is a contradiction.Hence Hd(ξ)(H(k)(ξ))n≡ξm. Since the multiplicity of all zeros of H is at leastby Lemmas 2.2,2.3 and 2.4,Hd(ξ)(H(k)(ξ))n−ξmhas at least two distinct zeros. Suppose that ξ0,ξ∗0are two distinct zeros of Hd(ξ)(H(k)(ξ))n−ξm.We choose a positive number δ small enough such that D1∩D2=∅and Hd(ξ)(H(k)(ξ))n−ξmhas no other zeros By Hurwitz’s theorem,there exists a subsequence ofwe still denote it asthen there exist pointsand points ξj→ξ0such that when j is large enough, Since,by the assumption in Theorem 1.6,share ψ(z),it follows that Thus,when j is large enough,This contradicts with the factsThus F1is normal at 0. where Thus we have Since we have On the other hand,for l=1,2,···,k,we have Thus we have spherically locally uniformly in C disjoint from the poles of g. If gd(ξ)(g(k)(ξ))n≡1,then g has no zeros.Of course,g also has no poles.Since g is a non-constant Meromorphic function of order at most 2,there exist constants ci(i= 1,2),(c1,c2)≠(0,0),andObviously,this is contrary to the case gd(ξ)(g(k)(ξ))n≡1.Hence Since the multiplicity of all zeros of g is at leastby Lemmas 2.2,2.3 and 2.4,gd(ξ)(g(k)(ξ))n−1 has at least two distinct zeros. By Hurwitz’s theorem,there exists a subsequence ofwe still denote it asThen there exist pointsand pointssuch that when j is large enough, Similar to the proof of Case 1.1,we get a contradiction.Then,F1is normal at 0. From Cases 1.1 and 1.2,we know that F1is normal at 0,and there exist∆={z:|z|<ρ} and a subsequence of Fj,we still denote it as Fj,such that Fjconverges spherically locally uniformly to a meromorphic function F(z)or∞in∆. Here we distinguish two cases. Case(i).When j is large enough,fj(0)≠0.Then F(0)=∞.Thus,for each Fj(z)∈F1, there exists a δ>0 such that if F(z)∈F1,then|F(z)|>1 for all z∈∆δ={z:|z|<δ}. Thus,for sufficiently large j,is holomorphic in∆δ.Therefore,for all fj∈F, when|z|=δ/2,we have By Maximum Principle and Montel’s Theorem,F is normal at z=0. Case(ii).There exists a subsequence of fj,we still denote it as fj,such that fj(0)=0. Since f∈F,the multiplicity of all zeros of f is at least p≥maxthen F(0)=0.Thus,there exists 0 By Cases(i)and(ii),F is normal at z=0. Case 2.ψ(z0)≠0. Suppose that F is not normal at z0.By Lemma 2.1 there exist a sequence{zj}of complex numbers with zj→z0,a sequence{ρn}of positive numbers with ρj→0 such that locally uniformly on compact subsets of C,where g(ξ)is a non-constant meromorphic function in C,all of whose zeros have multiplicity at leastMoreover, g(ξ)has order at most 2. Hence,by Lemmas 2.2,2.3 and 2.4,similar to the proof of Case 1.1,we get a contradiction.Thus F is normal at z0. [1]Hayman W H.Meromorphic Functions.Oxford:Clarendon Press,1964. [2]Tse C K,Yang C J.On the value distribution of fl(f(k))n.Kodai Math.J.,1994,17:163–169. [3]Yang C J,Hu P C.On the value distribution of ff(k),Kodai Math.J.,1996,19:157–167. [4]Yang C J,Yang L,Wang Y F.On the zeros of f(f(k))n−a.Chinese Sci.Bull.,1993,38: 2125–2128. [5]Fang M L,Zalcman L.On value distribution of f+a(f′)n(in Chinese).Sci.China,2008, 38A(3):279–285. [6]Wang Y F,Fang M L.Picard values and normal families of meromorphic functions with multiple zeros.Acta Math.Sinica(Chin.Ser.),1998,41(4):743–748. [7]Schwick W.Normality criteria for families of meromorphic function.J.Anal.Math.,1989,52: 241–289. [8]Li Y T,Gu Y X.On normal families of meromorphic functions.J.Math.Anal.Appl.,2009, 354:421–425. [9]Hu P C,Meng D W.Normality of meromorphic functions with multiple zeros.J.Math.Anal. Appl.,2009,357:323–329. [10]Jiang Y B,Gao Z S.Normal families of meromorphic functions sharing a holomorphic fnction and the converse of function Bloch principle.Acta Math.Sci.,2012,32B(4):1503–1512. [11]Zalman L.Normal families:new perspectives.Bull.Amer.Math.Soc.,1998,35(3):215–230. [12]Li G W,Su X F,Xu D J.On the zeros of fm(f(k))n−φ(z).J.Chongqing Norm.Univ(Nat. Sci),2013,30(4):73–76. date:May 27,2014. The NSF(11461070)of China. E-mail address:yangqi 8138@126.com(Yang Q).
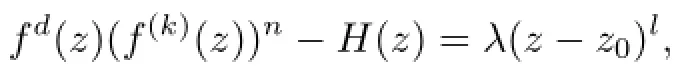
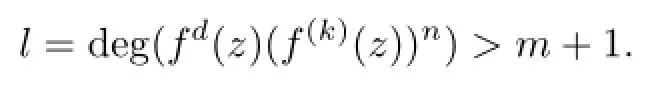
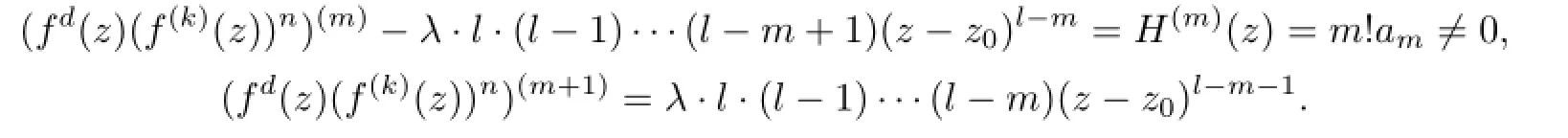
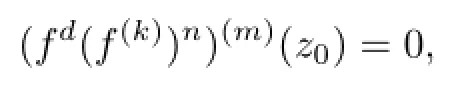
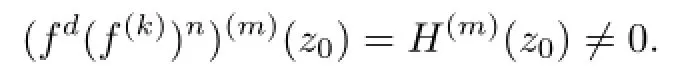
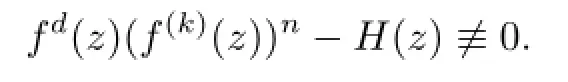
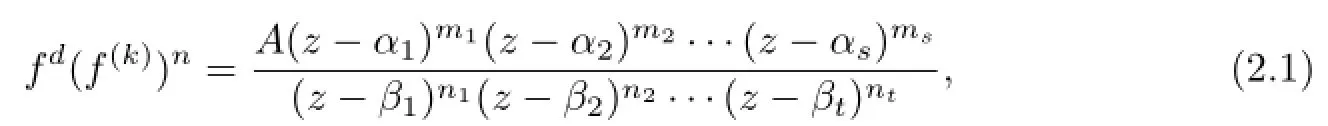
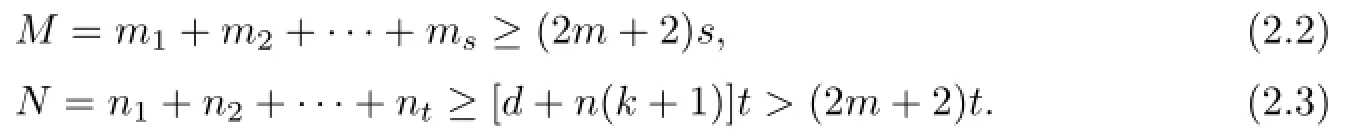
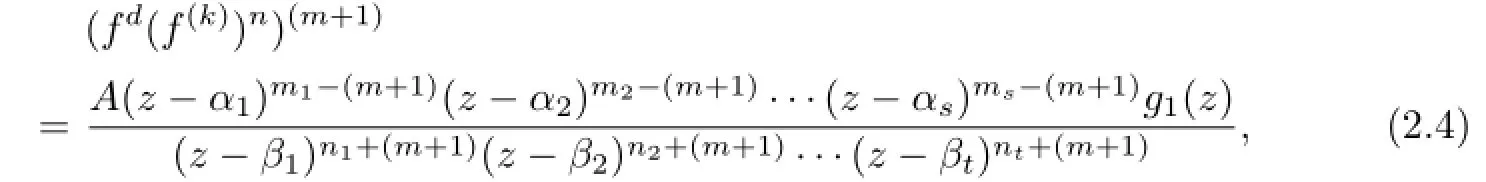
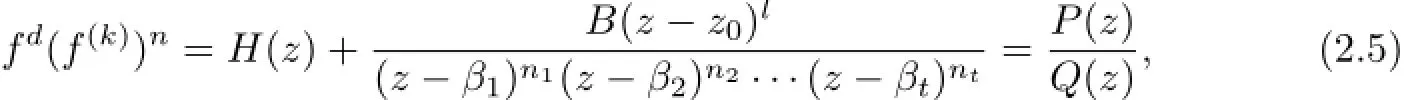
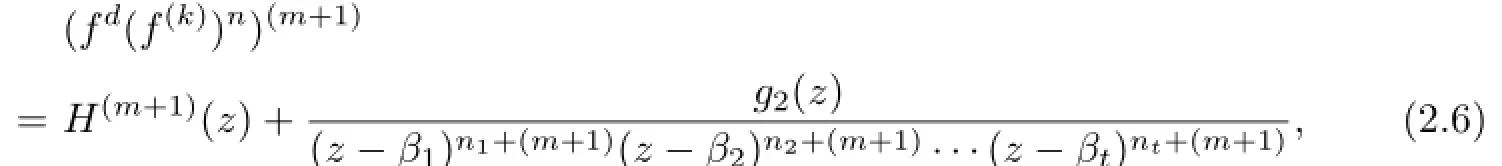
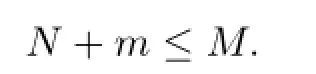
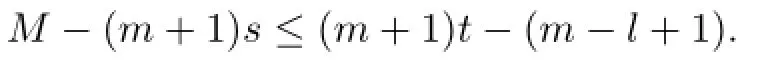
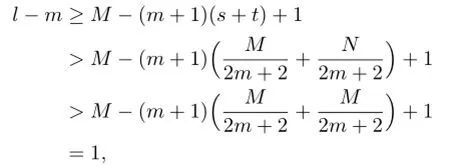
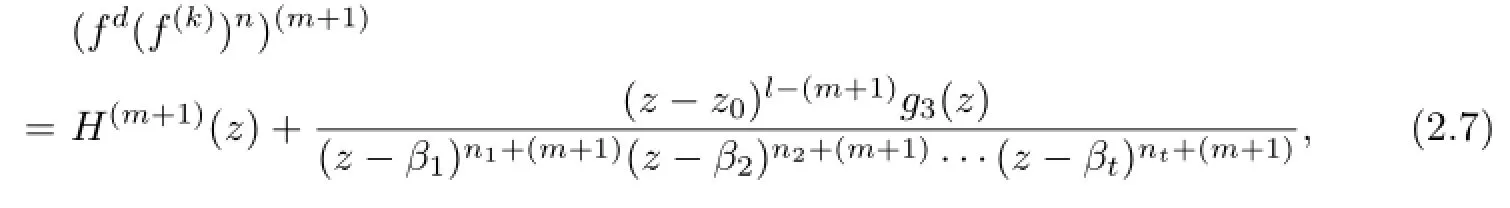
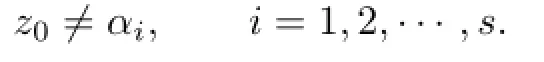
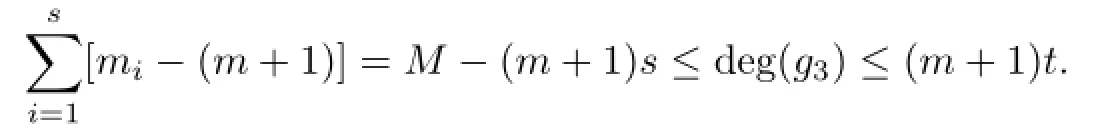

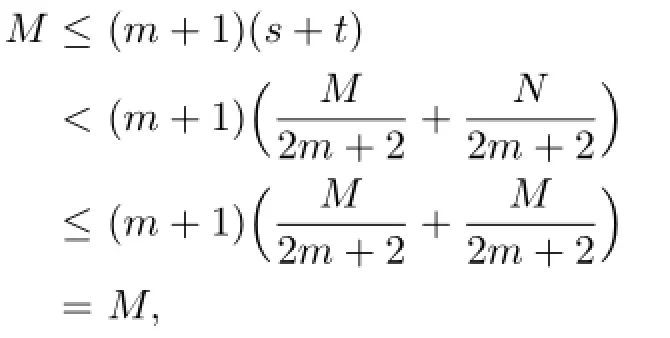

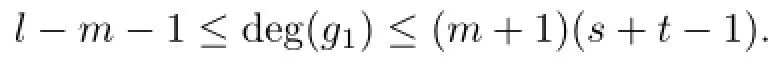
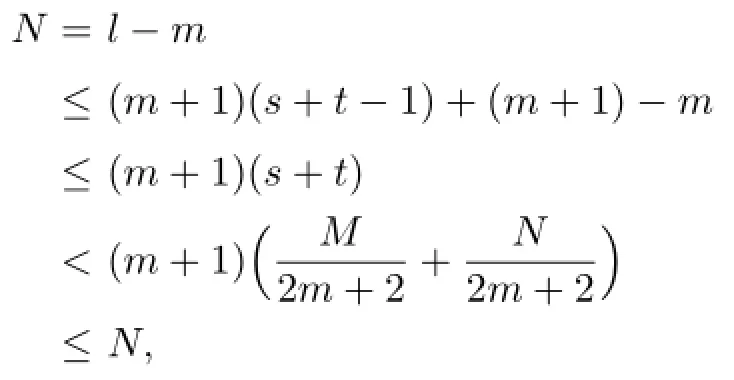
3 Proof of Theorem 1.6