Ore Extensions over Weakly 2-primal Rings
2016-10-12WangYaoJiangMeimeiandRenYanli
Wang Yao,Jiang Mei-meiand Ren Yan-li
(1.School of Mathematics and Statistics,Nanjing University of Information Science and Technology,Nanjing,210044)
(2.School of Mathematics and Information Technology,Nanjing Xiaozhuang University, Nanjing,211171)
Communicated by Du Xian-kun
Ore Extensions over Weakly 2-primal Rings
Wang Yao1,Jiang Mei-mei1and Ren Yan-li2,*
(1.School of Mathematics and Statistics,Nanjing University of Information Science and Technology,Nanjing,210044)
(2.School of Mathematics and Information Technology,Nanjing Xiaozhuang University, Nanjing,211171)
Communicated by Du Xian-kun
A weakly 2-primal ring is a common generalization of a semicommutative ring,a 2-primal ring and a locally 2-primal ring.In this paper,we investigate Ore extensions over weakly 2-primal rings.Let α be an endomorphism and δ an αderivation of a ring R.We prove that(1)If R is an(α,δ)-compatible and weakly 2-primal ring,then R[x;α,δ]is weakly semicommutative;(2)If R is(α,δ)-compatible, then R is weakly 2-primal if and only if R[x;α,δ]is weakly 2-primal.
(α,δ)-compatible ring,weakly 2-primal ring,weakly semicommutative ring,nil-semicommutative ring,Ore extension
2010 MR subject classification:16S50,16U20,16U80
Document code:A
Article ID:1674-5647(2016)01-0070-13
10.13447/j.1674-5647.2016.01.05
1 Introduction
Throughout this paper,R denotes an associative ring with identity,α is an endomorphism of R and δ is an α-derivation of R,that is,δ is an additive map such that δ(ab)=δ(a)b+ α(a)δ(b)for a,b∈R.We denote by R[x;α,δ]the Ore extension whose elements are the polynomials over R,the addition is defined as usual,and the multiplication subject to the reaction xr=α(r)x+δ(r)for any r∈R.Particularly,if δ=0R,we denote by R[x;α] the skew polynomial ring;if α=1R,we denote by R[x;δ]the differential polynomial ring. For a ring R,we denote by nil(R)the set of all nilpotent elements of R,Nil∗(R)its lower nil-radical,Nil∗(R)its upper nil-radical and L-rad(R)its Levitzki radical.For a nonempty subset M of a ring R,the symbol⟨M⟩denotes the subring(may not with 1)generated by M.
Recall that a ring R is called reduced if it has no nonzero nilpotent elements;R is symmetric if abc=0 implies acb=0 for all a,b,c∈R;R is semicommutative if ab=0 implies aRb=0 for all a,b∈R.In[1],semicommutative property is called the insertionof-factors-property,or IFP.There are many papers to study semicommutative rings and their generalization(see[2]–[5]).Liu and Zhao([6],Lemma 3.1)has proved that if R is a semicommutative ring,then nil(R)is an ideal of R.Liang et al.[5]called a ring R to be weakly semicommutative if ab=0 implies aRb⊆nil(R)for any a,b∈R.This notion is a proper generalization of semicommutative rings by Example 2.2 in[5].According to Chen[2],a ring R is called nil-semicommutative if ab∈nil(R)implies aRb⊆nil(R)for any a,b∈R.A nil-semicommutative ring is weakly semicommutative,but the converse is not true by Example 2.2 in[2].Recall that a ring R is 2-primal if nil(R)=Nil∗(R).Hong et al.[7]called a ring R to be locally 2-primal if each finite subset generates a 2-primal ring, and have shown that if R is a nil ring then R is locally 2-primal if and only if R is a Levitzki radical ring.Chen and Cui[3]called a ring R to be weakly 2-primal if the set of nilpotent elements in R coincides with its Levitzki radical,that is,nil(R)=L-rad(R).Due to Marks[8], a ring R is called NI if nil(R)=Nil∗(R).It is obvious that a ring R is NI if and only if nil(R)forms an ideal,if and only if R/Nil∗(R)is reduced.Hwang et al.[9]considered basic structure and some extensions of NI rings,and Proposition 2.1 in[3]has presented their some characterizations.The following implications hold:
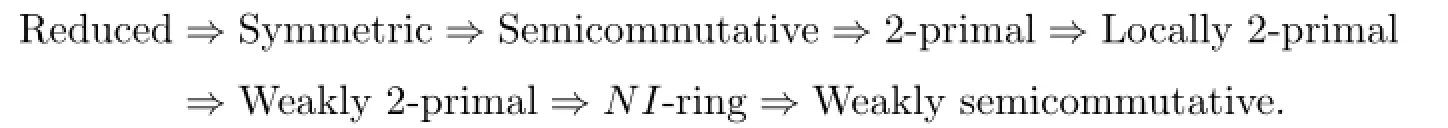
In general,each of these implications is irreversible(see[3],[7]).
According to Annin[10],for an endomorphism α and an α-derivation δ,a ring R is said to be α-compatible if for each a,b∈R,ab=0⇔ aα(b)=0.Moreover,R is called to be δ-compatible if for each a,b∈R,ab=0⇒ aδ(b)=0.If R is both α-compatible and δ-compatible,R is called(α,δ)-compatible.Liang et al.[5]have proved that if R is α-compatible semicommutative,then R[x;α]is weakly semicommutative.Chen and Cui[3]have shown that if R is weakly 2-primal and α-compatible,then R[x;α]is weakly 2-primal and hence weakly semicommutative.In this paper,we extend respectively the above results to more general cases,the Ore extensions over weakly 2-primal rings,and generalize recent some related work on polynomial rings and skew polynomial rings.In particular,we show that if R is an(α,δ)-compatible and weakly 2-primal ring,then R[x;α,δ]is a weakly semicommutative ring;if R is(α,δ)-compatible,then R is weakly 2-primal if and only if R[x;α,δ]is weakly 2-primal.At the same time,we also extend a main result proved by Chen[2]to the Ore extensions R[x;α,δ]over weakly 2-primal ring,and obtain that if R is an(α,δ)-compatible and weakly 2-primal ring,then R[x;α,δ]is a nil-semicommutative ring.
In the following,for integers i,j withdenotes the map which is the sum of all possible words in α,δ built with i letters α and j−i letters δ.For instance,In particular,with 0≤i≤j,it hasmonomials in α,δ built with i letters α and j−i letters δ.As is known to all that for any integer n and r∈R,we havein the ring R[x;α,δ].
2 Weakly Semicommutative Property of R[x;α,δ]
In this section,we discuss the weakly semicommutative property and nil-semicommutative property of Ore extensions R[x;α,δ]over weakly 2-primal rings.In general,one may suspect that if R is(α,δ)-compatible,then R is weakly semicommutative(resp.,nil-semicommutative) if and only if R[x;α,δ]is weakly semicommutative(resp.,nil-semicommutative).Since any subring of a weakly semicommutative(resp.,nil-semicommutative)ring is also a weakly semicommutative(resp.,nil-semicommutative)ring,it is clear that if R[x;α,δ]is weakly semicommutative(resp.,nil-semicommutative),then R is weakly semicommutative(resp., nil-semicommutative).Unfortunately,the converse is negative.Chen([2],Theorem 2.6)has proved that there exists a nil-semicommutative ring R over which the polynomial ring R[x] is not nil-semicommutative.Example 2.1 in the following shows that there exists a weakly semicommutative ring R over which the polynomial ring R[x]is not weakly semicommutative.
Example 2.1[4]Let Z2be the field of integers modulo 2 and S=Z2⟨a0,a1,a2,b0,b1, b2,c⟩be the free algebra in noncommuting indeterminates a0,a1,a2,b0,b1,b2,c over Z2. Let A=Z2[a0,a1,a2,b0,b1,b2,c]be the subalgebra in S,of polynomials with zero constant terms.Note that A is a ring without identity and consider an ideal of Z2+A,say I,generated by a0b0,a0b1+a1b0,a0b2+a1b1+a2b0,a1b2+a2b1,a2b2,a0rb0,(a0+a1+a2)r(b0+b1+b2) with r∈A and r1r2r3r4with r1,r2,r3,r4∈A.Then,clearly,A4∈I.Let T=(Z2+A)/I. Then T is semicommutative by Example 2 in[5].Thus R=T[x]is weakly semicommutative by Corollary 3.1 in[5].Next we prove that R[y]is not weakly semicommutative.Notice that(a0+a1x+a2x2)(b0+b1x+b2x2)∈I[x],then
(a0+(a0+a1x)y+(a0+a1x+a2x2)y2)(b0+(b0+b1x)y+(b0+b1x+b2x2)y2)∈I[x][y], but
(a0+(a0+a1x)y+(a0+a1x+a2x2)y2)c(b0+(b0+b1x)y+(b0+b1x+b2x2)y2)/∈I[x][y] since a0cb1+a1cb0/∈I.Therefore,T[x]is not weakly semicommutative.
To prove the main results of this section,we need the following lemma and several propositions.
Lemma 2.1[11]Let R be an(α,δ)-compatible ring.Then
(1)If ab=0,then aαn(b)=αn(a)b=0 for all positive integers n;
(2)If αk(a)b=0 for some positive integer k,then ab=0;
(3)If ab=0,then αn(a)δm(b)=δm(a)αn(b)=0 for all positive integers m,n.
Proposition 2.1Let R be an(α,δ)-compatible ring.Then
(1)If ab=0,then afji(b)=0 for all 0≤i≤j and a,b∈R;
(2)For a,b∈R and any positive integer m,ab∈nil(R)if and only if aαm(b)∈nil(R).Proof.(1)If ab=0,then aαi(b)=aδj(b)=0 for all i≥0 and j≥0 by Lemma 2.1. Hence
(2)It is an immediate consequence of Lemma 3.1 in[5]and Lemma 2.8 in[12].
Proposition 2.2Let R be an(α,δ)-compatible ring.Then
(1)If abc=0,then aδ(b)c=0 for any a,b,c∈R;
(3)If ab∈nil(R),then aδ(b)∈nil(R)for any a,b∈R.
Proof.(1)If abc=0,we have α(ab)δ(c)=0,α(a)α(b)δ(c)=0 and aα(b)δ(c)=0.On the other hand,we also have aδ(bc)=0,a(δ(b)c+α(b)δ(c))=0 and aδ(b)c+aα(b)δ(c)=0.So aδ(b)c=0.
(2)If abc=0,we have aα(bc)=0,aα(b)α(c)=0 and aα(b)c=0.It follows that aαm(b)c=0 and aδnαm(b)c=0 for any positive integers m,n.Meanwhile,we can obtain that aδ(b)c=0 by(1),which implies that aδj(b)c=0 and aαiδj(b)c=0.Therefore,we have
(3)Since ab∈nil(R),there exists some positive integer k such that(ab)k=0.In the following computations,we use freely(1):
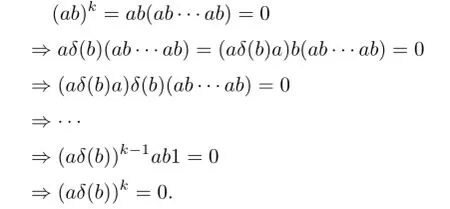
This implies that aδ(b)∈nil(R).
Proposition 2.3If R is an(α,δ)-compatible NI ring,then ab∈nil(R)implies∈ nil(R)for all 0≤i≤j and a,b∈R.
Proof.If ab∈nil(R),then we have aαi(b),aδj(b)∈nil(R)for all i≥0 and j≥0 by Propositions 2.1 and 2.2.This implies aδjαi(b),aαiδj(b)∈nil(R).Since R is NI,we have
Proposition 2.4Let R be an(α,δ)-compatible NI ring,andThen f(x)g(x)=0 implies aibj∈nil(R)for each i,j.
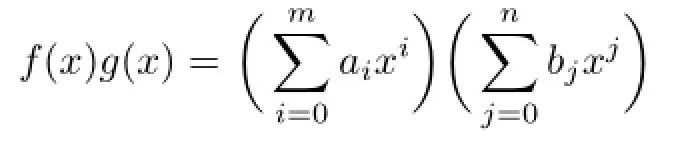
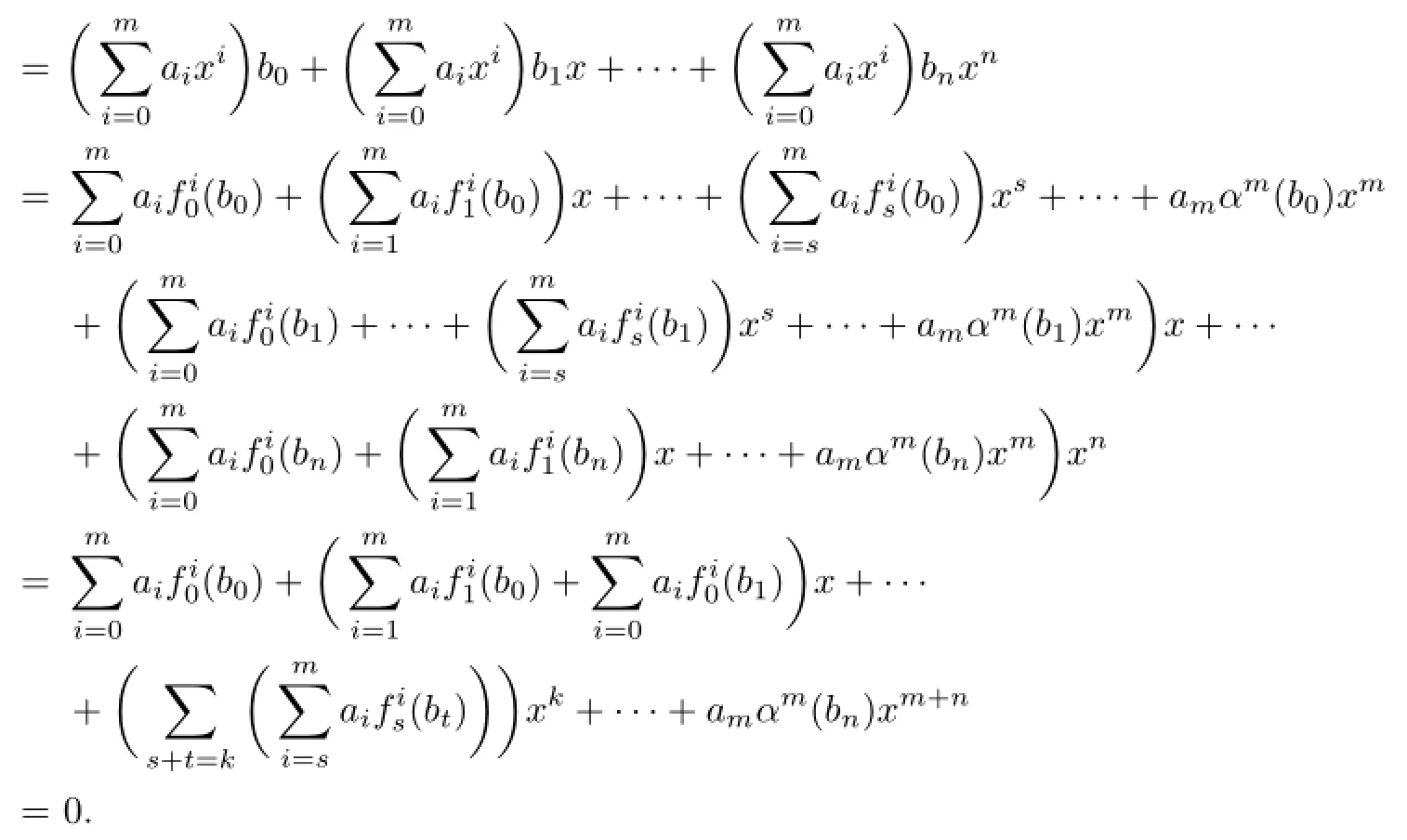
It follows that
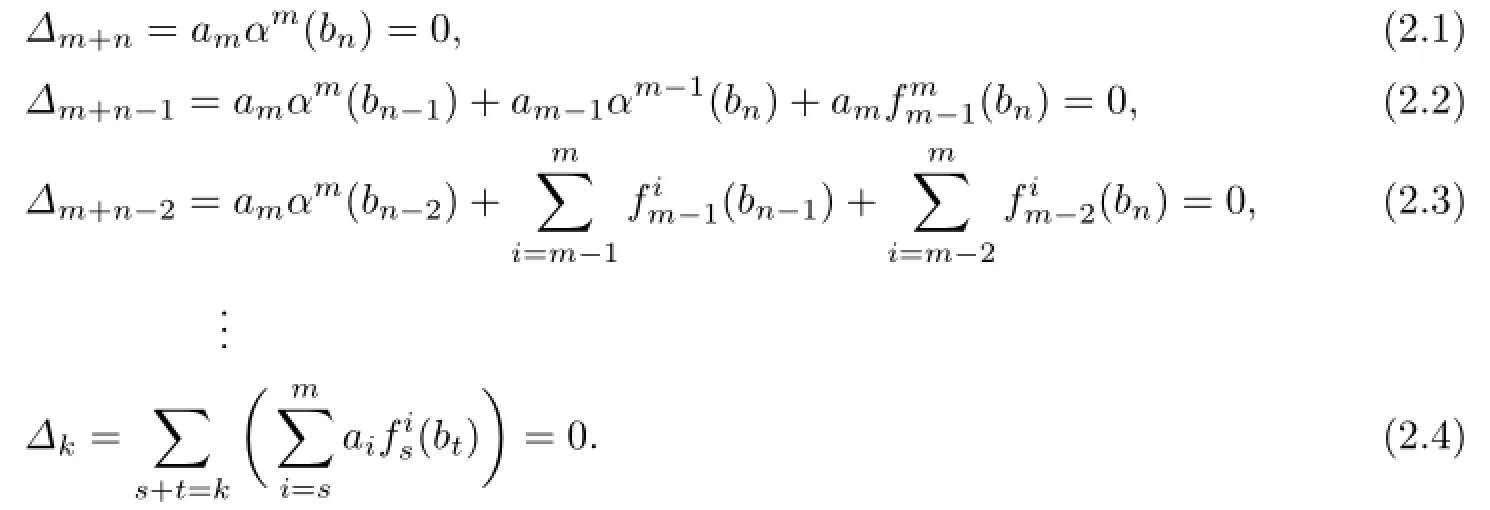
From(2.1),we have ambn=0 since R is(α,δ)-compatible.Thus,by Proposition 2.1,for all 0≤s≤t.From(2.2),we have

If we multiply(2.5)on the left side by bn,then we obtain

Since ambn=0,we have bnam∈nil(R).So
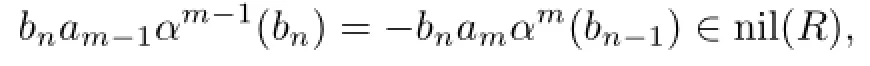
because the nil(R)of an NI ring R is an ideal.Thus,bnam−1bn∈nil(R)by Proposition 2.1,and hence bnam−1∈nil(R),am−1bn∈nil(R)and am−1αm−1(bn)∈nil(R).It follows that amαm(bn−1)∈nil(R)and so ambn−1∈nil(R)by Proposition 2.1.Therefore, ambn−1,am−1bn∈nil(R).By Proposition 2.3 and(2.3),

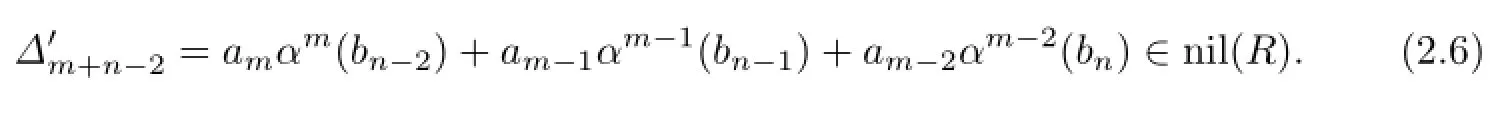
we haveIf we multiply(2.6)on the left side by bn,bn−1,bn−2,respectively,then we obtain am−2bn∈nil(R),am−1bn−1∈nil(R)and ambn−2∈nil(R)in turn.
Continuing this procedure yields that aibj∈nil(R)for all i,j.
The index of nilpotency of a nilpotent element x in a ring R is the least positive integer n such that xn=0.The index of nilpotency of a subset I of R is the supremum of the indices of nilpotency of all nilpotent elements in I.If such a supremum is finite,then I is said to be of bounded index of nilpotency.
Proposition 2.5Let R be(α,δ)-compatible and
(1)If R is an NI ring,then f(x)∈nil(R[x;α,δ])implies ai∈nil(R)for all 0≤i≤n;
(2)If R is a weakly 2-primal ring,then ai∈nil(R)for all 0≤i≤n implies f(x)∈nil(R[x;α,δ]);
(3)If Nil∗(R)is nilpotent,then ai∈nil(R)for 0≤i≤n implies f(x)∈nil(R[x;α,δ]);
(4)If R is of bounded index of nilpotency,then ai∈nil(R)for all 0≤i≤n implies f(x)∈nil(R[x;α,δ]).

Hence
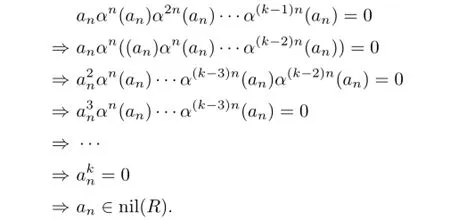
So by Proposition 2.3,an=1·an∈nil(R)impliesfor all 0≤s≤t.Let Q=a0+a1x+···+an−1xn−1.Then
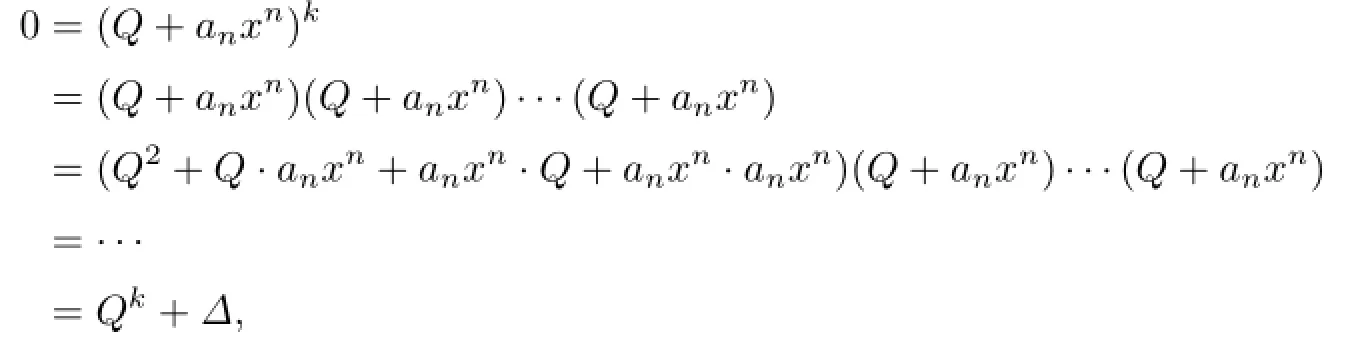
where∆∈R[x;α,δ].Notice that the coefficients of∆can be written as sums of monomials in aiand,where ai,aj∈{a0,a1,···,an}and 0≤u≤v are positive integers,andeach monomial hasSince nil(R)is an ideal of R,we obtain that each monomial is in nil(R),and then∆∈nil(R)[x;α,δ].Thus
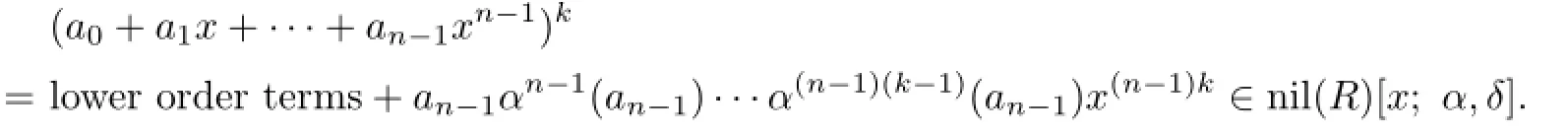
Hence,by Proposition 2.3,
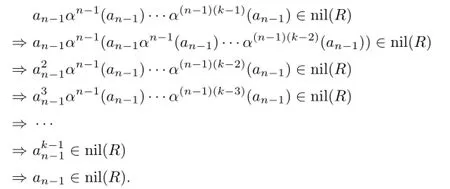
By using induction on n,we have ai∈nil(R)for all 0≤i≤n.
(2)Consider the finite subset{a0,a1,···,an}.Since R is weakly 2-primal and hence nil(R)=L-rad(R),⟨a0,a1,···,an⟩is nilpotent subring of R.So there exists a positive integer k such that any product of k elements ai1ai2···aikfrom{a0,a1,···,an}is zero.Note that the coefficients ofin R[x;α,δ]can be written as sums of monomials of length k+1 in aiand,where ai,aj∈{a0,a1,···,an}and 0≤u≤v are positive integers.For each monomial,where ai1,ai2,···,aik+1∈ {a0,a1,···,an}and tj,sj(tj≥sj,2≤j≤k+1)are nonnegative integers,we obtainby Propositions 2.1 and 2.2.Therefore,we have f(x)k+1=0 and so f(x)∈nil(R[x;α,δ]).
(3)In this case,nil(R)=Nil∗(R)=L-rad(R),the proof is similar to that of(2).
(4)By Proposition 22.2 in[13],in this case,R is locally nilpotent,and hence nil(R)= Nil∗(R)=L-rad(R)=R.
Corollary 2.1Let R be a weakly 2-primal ring.If R is(α,δ)-compatible,then
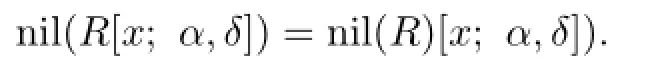
Corollary 2.2Let R be(α,δ)-compatible.Then
(1)If R is weakly 2-primal,then R[x;α,δ]is NI;
(2)If Nil∗(R)is nilpotent,then R[x;α,δ]is NI;
(3)If R is of bounded index of nilpotency,then R[x;α,δ]is NI.
Proof.Since nil(R)[x;α,δ]is an ideal of R[x;α,δ]),we have
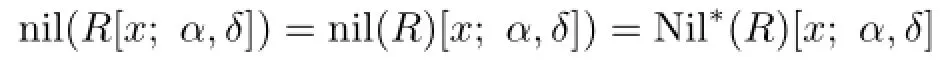
by Proposition 2.5.
Corollary 2.3Let R be a weakly 2-primal ring.Then nil(R[x])=nil(R)[x].
Proposition 2.6Let R be an(α,δ)-compatible weakly 2-primal ring.Then,for f(x)=and c∈R,we have
(1)fg∈nil(R[x;α,δ])⇔aibj∈nil(R)for all 0≤i≤m,0≤j≤n;
(2)fgc∈nil(R[x;α,δ])⇔aibjc∈nil(R)for all 0≤i≤m,0≤j≤n;
(3)fgh∈nil(R[x;α,δ])⇔aibjck∈nil(R)for all 0≤i≤m,0≤j≤n and 0≤k≤p.
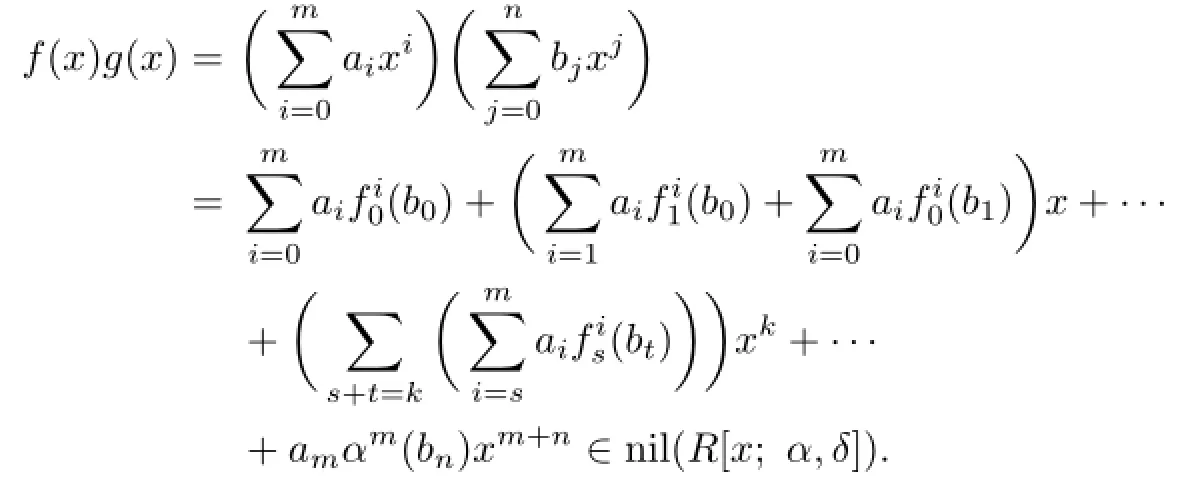
Thus,by Proposition 2.5,we have that

From Proposition 2.1 and(2.7),we have ambn∈nil(R).Next we show that aibn∈nil(R) for all 0≤i≤m.If we multiply(2.8)on the left side by bn,then bnam−1αm−1(bn)∈nil(R) since nil(R)is an ideal of R.Thus,by Proposition 2.1,bnam−1bn∈nil(R),and so bnam−1∈nil(R),am−1bn∈nil(R).Multiplying(2.9)on the left side by bn,since nil(R)is an ideal of R,we obtain
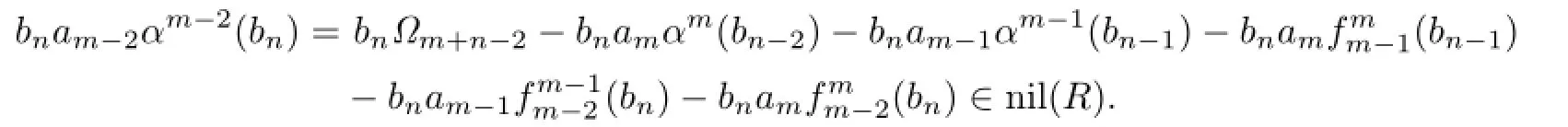
Thus bnam−2∈nil(R)and am−2bn∈nil(R).Continuing this procedure yields that aibn∈ nil(R)for all 0≤i≤m,and sofor any 0≤s≤t and 0≤i≤m by Proposition 2.3.Thus it is easy to verify that
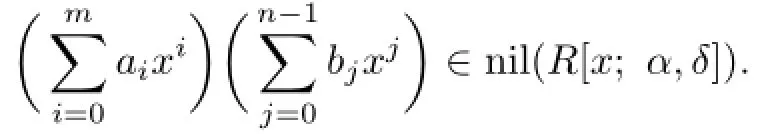
Applying the preceding method repeatedly,we obtain that aibj∈nil(R)for all 0≤i≤m and 0≤j≤n.
⇐.Let aibj∈nil(R)for all i,j.Thenfor all i,j and all positive integers 0≤s≤i by Proposition 2.3.Thus
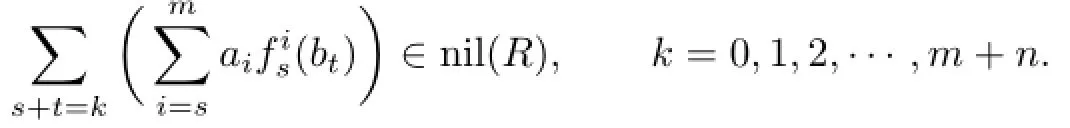
Hence,by Proposition 2.5,
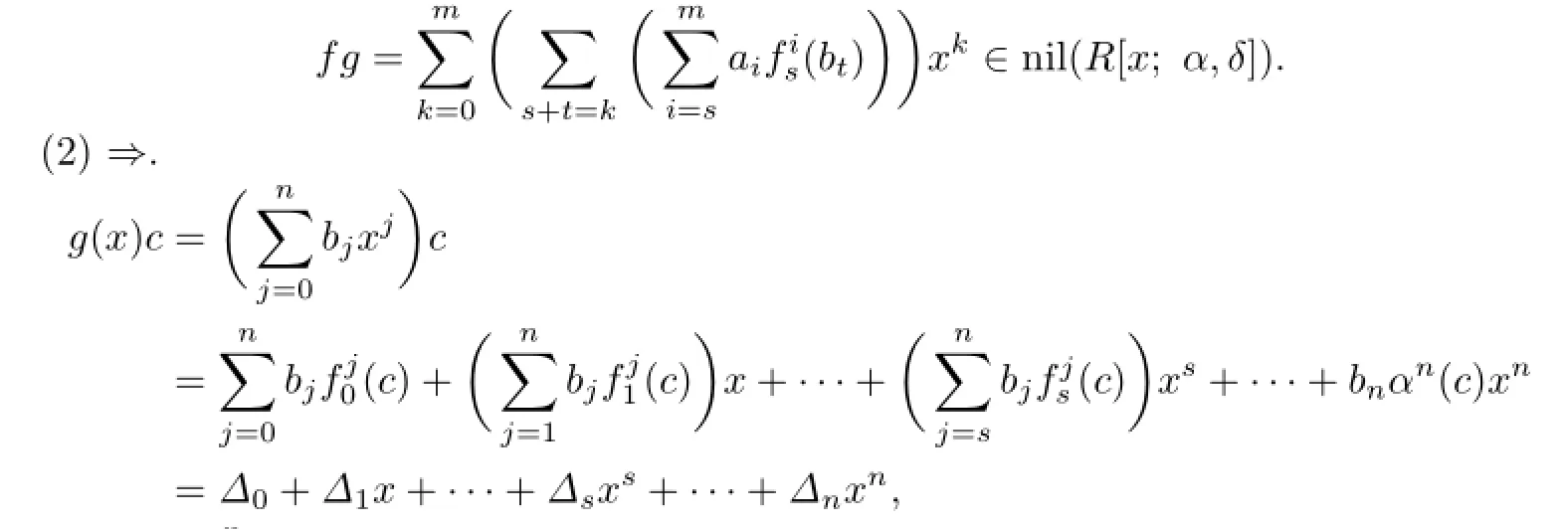
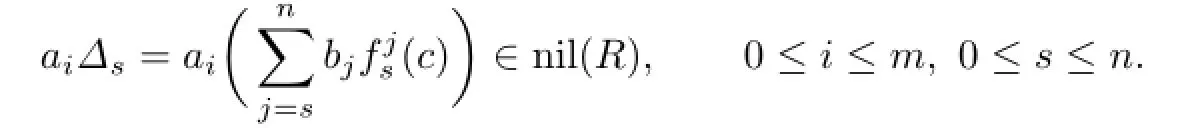
For s=n,we have
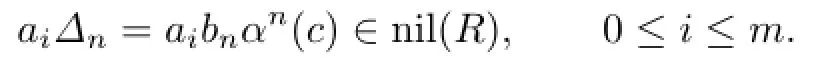
Then,by Proposition 2.1,aibnc∈nil(R)for all 0≤i≤m.
For s=n−1,we have
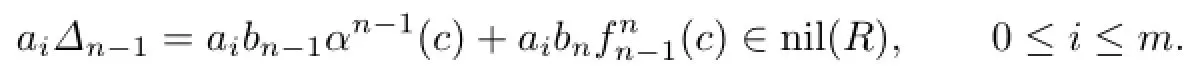
Since aibnc∈nil(R),by Proposition 2.3,we haveHence
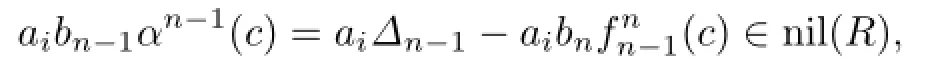
and so aibnc∈nil(R)for all 0≤i≤m.
Now suppose that k is a positive integer such that aibjc∈nil(R)for all 0≤i≤m when j>k.We show that aibkc∈nil(R)for all 0≤i≤m.
If s=k,for all 0≤i≤m,we have
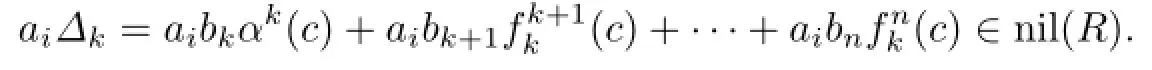
Since aibjc∈nil(R)for 0≤i≤m and k It follows that aibkαk(c)∈nil(R),and hence aibkc∈nil(R)for all 0≤i≤m.By induction, we obtain that aibjc∈nil(R)for all 0≤i≤m and 0≤j≤n. ⇐.Suppose that aibjc∈nil(R)for all 0≤i≤m and 0≤j≤n.Then∈ nil(R),and sofor all 0≤i≤m and 0≤j≤n.By(1),we obtain fgc∈nil(R[x;α,δ]). (3) ⇒.First we show that fgh∈nil(R[x;α,δ])implies fgck∈nil(R[x;α,δ])for all 0≤k≤p.For any 0≤k≤p,since fgh∈nil(R[x;α,δ]),by(1),we have and so fgck∈nil(R[x;α,δ])with k∈0,1,···,p.Now(2)implies that aibjck∈nil(R)for all 0≤i≤m,0≤j≤n and 0≤k≤p. ⇐.Suppose that aibjck∈nil(R)for all 0≤i≤m,0≤j≤n and 0≤k≤p.Then we have fgck∈nil(R[x;α,δ])for all 0≤k≤p,and so∆lck∈nil(R)for all 0≤l≤m+n and 0≤k≤p by(2).Therefore,(1)implies fgh∈nil(R[x;α,δ]). Theorem 2.1Let R be a weakly 2-primal ring.If R is(α,δ)-compatible,then R[x;α,δ] is weakly semicommutative. Corollary 2.4If R is a weakly 2-primal ring,then R[x]is weakly semicommutative. Corollary 2.5If R is an α-compatible and weakly 2-primal ring,then R[x;α]is a weakly semicommutative ring. Corollary 2.6If R is a δ-compatible and weakly 2-primal ring,then R[x;δ]is a weakly semicommutative ring. Chen([2],Theorem 2.6)has shown that there exists a nil-semicommutative ring R over which the polynomial ring R[x]is not nil-semicommutative.Nevertheless,we obtain that if R is semicommutative,then R[x]is nil-semicommutative.For the more general case,we have the following theorem. Theorem 2.2Let R be a weakly 2-primal ring.If R is(α,δ)-compatible,then R[x;α,δ] is nil-semicommutative. Corollary 2.7If R is a weakly 2-primal ring,then R[x]is nil-semicommutative. Corollary 2.8[2]Let R be a weakly 2-primal ring.If R is an α-compatible ring,then R[x;α]is nil-semicommutative. Corollary 2.9Let R be a weakly 2-primal ring.If R is a δ-compatible ring,then R[x;δ] is nil-semicommutative. In this section,we consider the relationship between the properties of being the weakly 2-primal of a ring R and that of the Ore extension R[x;α,δ]. Lemma 3.1[3]Let R be an(α,δ)-compatible ring.If k1,k2,···,knare arbitrary nonnegative integers and a1,a2,···,anare arbitrary elements in R,then Proposition 3.1Let R be an(α,δ)-compatible ring.Then (1)If a1a2···an=0,then δk1(a1)δk2(a2)···δkn(an)=0,where k1,k2,···,knare arbitrary nonnegative integers and a1,a2,···,anare arbitrary elements in R; (2)If a1a2···an=0,thenfor all ai∈R and 0≤si≤ti, i=1,2,···,n. Proof.(1)Let abc=0 for all a,b,c∈R.We have aδ(b)c=0 by Proposition 2.2.According to Lemma 2.1 and δ-compatibility,we have δ(a)δ(b)δ(c)=0.Thus a1a2···an=0 implies (2)It is an immediate consequence of(1)and Lemma 3.1. Theorem 3.1Let R be(α,δ)-compatible.Then R is weakly 2-primal if and only if R[x;α,δ]is weakly 2-primal. Proof.By Proposition 3.1 in[3],each subring of weakly 2-primal rings is weakly 2-primal. So we just to prove the necessity. Since R is weakly 2-primal,L-rad(R)=nil(R),and so R/nil(R)is reduced.The endomorphism α of R induces an endomorphismof R/nil(R)viasince α(nil(R))⊆nil(R).And the α-derivation δ of R also induces anderivationof R/nil(R)via We need to prove that nil(R[x;α,δ])=L-rad(R[x;α,δ]).It is enough to show that nil(R[x;α,δ])⊆L-rad(R[x;α,δ])since the reverse inclusion is obvious.It is a routine task to check that there exists an onto ring homomorphism First we show that nil(R[x;α,δ])⊆nil(R)[x;α,δ]=L-rad(R)[x;α,δ].Suppose thatis nilpotent with the nilpotent index k in R[x;α,δ].Then inBecause R/nil(R)is reduced andcompatible,we can obtainfor all 0≤i≤n by Proposition 2.5.Hence ai∈nil(R)for all 0≤i≤n.Thus nil(R[x;α,δ])⊆nil(R)[x;α,δ]=L-rad(R)[x;α,δ]. Next we prove that L-rad(R)[x;α,δ]is locally nilpotent.Suppose that We prove that the finitely generated subring(without 1)W=⟨f1(x),f2(x),···,fk(x)⟩of L-rad(R)[x;α,δ]is nilpotent.Write fi(x)=ai0+ai1x+···+ainxn,where aijis in L-rad(R) for all i=1,2,···,k;j=0,1,2,···,n.Let M={ai0,ai1,···,ain|i=1,2,···,k}. Then M is a finite subset of L-rad(R).So the subring⟨M⟩(without 1)generated by M is nilpotent.There exists a positive integer p such that⟨M⟩p=0.Hence for any b1,b2,···,bp∈⟨M⟩,we have b1b2···bp=0.Now we prove that Wp=0.In fact,for any g1(x),g2(x),···,gp(x)∈W,we may write gj(x)=bj0+bj1x+···+bjmxm,j=1,2,···,p. It is easy to see that bjt∈M for all j and t=0,1,2,···,m.Note that It is easy to check that the coefficients of g1(x)g2(x)···gp(x)can be written as sums of monomials of length p in bjiand,whereand 0≤u≤v are positive integers.Consider each monomialwhereand tj,sj(0≤sj≤tj,1≤j≤p−1) are nonnegative integers.Sincewe haveHenceby Proposition 3.1.It follows that g1(x)g2(x)···gp(x)=0, and so L-rad(R)[x;α,δ]is locally nilpotent.Since nil(R)=L-rad(R)is an ideal of R and α(nil(R))⊆nil(R)and δ(nil(R))⊆nil(R),L-rad(R)[x;α,δ]is an ideal of R[x;α,δ].Noting that L-rad(R)[x;α,δ]is locally nilpotent,we have L-rad(R)[x;α,δ]⊆L-rad(R[x;α,δ]). From the above argument,we have Corollary 3.1Let R be a weakly 2-primal ring.If R is(α,δ)-compatible,then R[x;α,δ] is NI and weakly semicommutative. Corollary 3.2[3]Let R be α-compatible.Then R is weakly 2-primal if and only if R[x;α] is weakly 2-primal. Corollary 3.3Let R be δ-compatible.Then R is weakly 2-primal if and only if R[x;δ] is weakly 2-primal. [1]Bell H E.Near-rings in which each element is a power of itself.Bull.Austral.Math.Soc.,1970, 2:363–368. [2]Chen W.On nil-semicommutative rings.Thai J.Math.,2011,9(1):39–47. [3]Chen W,Cui S.On weakly semicommutative rings.Comm.Math.Res.,2011,27(2):179–192. [4]Huh C,Lee Y C,Smoktunowicz A.Armendariz rings and semicommutative rings.Comm. Algebra,2002,30(2):751–761. [5]Liang L,Wang L,Liu Z.On a generalization of semicommutative rings.Taiwanese J.Math., 2007,11(5):1359–1368. [6]Liu Z,Zhao R.On weak Armendariz rings.Comm.Algebra,2006,34:2607–2616. [7]Hong C Y,Kim H K,Kim N K,Kwak T K,Lee Y,Park K S.Rings whose nilpotent elements form a Levitzki radical ring.Comm.Algebra,2007,35:1379–1390. [8]Marks G.On 2-primal Ore extensions.Comm.Algebra,2001,29(5):2113–2123. [9]Hwang S U,Jeon Y C,Lee Y.Structure and topological conditions of NI rings.J.Algebra, 2006,302:186–199. [10]Annin S.Associated primes over skew polynomials rings.Comm.Algebra,2002,30:2511–2528. [11]Hashemi E,Moussavi A.Polynomial extensions of quasi-Baer rings.Acta Math.Hungar.,2005, 107(3):207–224. [12]Ouyang L,Chen H.On weak symmetric rings.Comm.Algebra,2010,38:697–713. [13]Szasz F A.Radicals of Rings.New York:John Wiley and Sons,1981. date:June 17,2014. The NSF(11071097,11101217)of China and the NSF(BK20141476)of Jiangsu Province. . E-mail address:wangyao@nuist.edu.cn(Wang Y),renyanlisx@163.com(Ren Y L).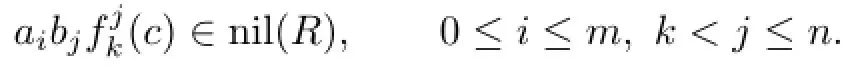
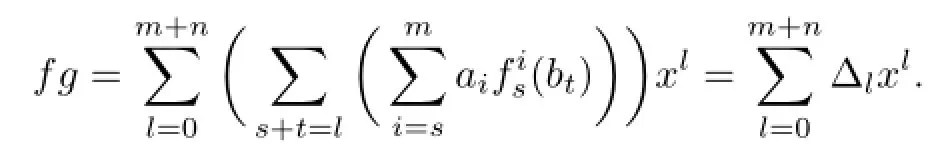
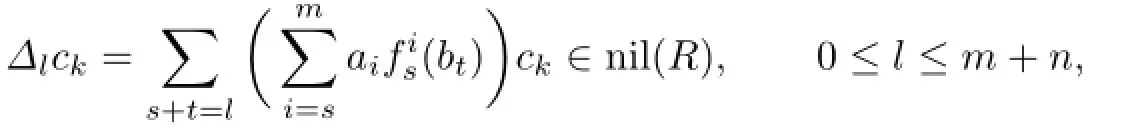
3 Weakly 2-primal Property of R[x;α,δ]
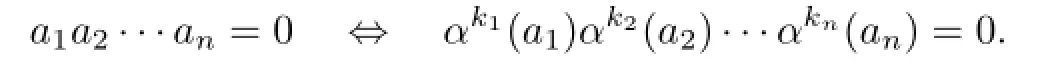
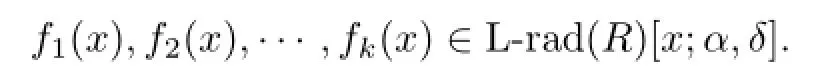
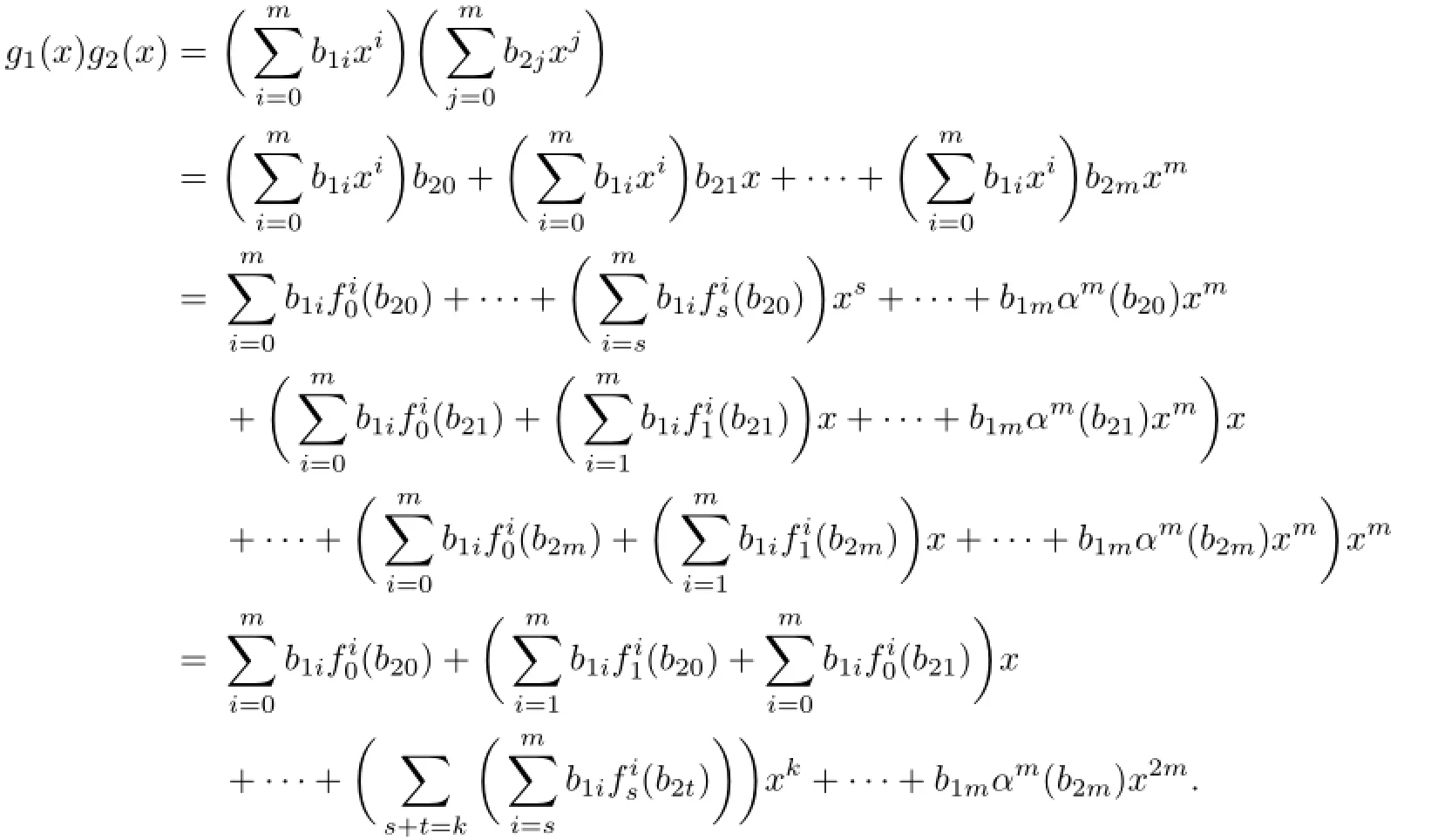
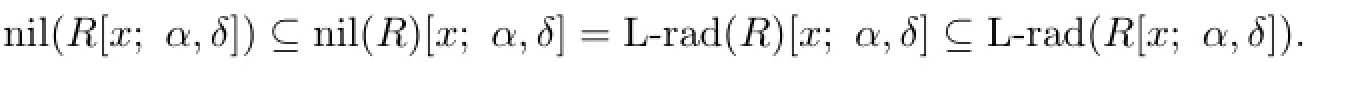
杂志排行
Communications in Mathematical Research的其它文章
- Normality Criteria of Meromorphic Functions
- An Identity with Skew Derivations on Lie Ideals
- L-octo-algebras
- Normality Criteria of Meromorphic Functions Concerning Shared Analytic Function
- A New Generalized FB Complementarity Function for Symmetric Cone Complementarity Problems
- Triple Crossing Numbers of Graphs
