水平轴潮流能捕获桨叶设计流速研究
2016-10-12李江花姜楚华陈俊华杨灿军
林 躜,张 利,李江花,姜楚华,陈俊华,杨灿军
(1.浙江大学 机械工程学院,浙江 杭州 310027; 2.浙江大学 宁波理工学院,浙江 宁波 315100; 3.太原科技大学 机械工程学院,山西 太原 030024)
水平轴潮流能捕获桨叶设计流速研究
林 躜1,2,张 利3,李江花3,姜楚华2,陈俊华2,杨灿军1
(1.浙江大学 机械工程学院,浙江 杭州 310027; 2.浙江大学 宁波理工学院,浙江 宁波 315100; 3.太原科技大学 机械工程学院,山西 太原 030024)
针对定桨距桨叶在时变潮流流速中设计流速选取的关键问题,应用叶素动量与流体动力学理论,建立变流速中设计流速与桨叶捕获功率之间的数学模型。结合韭山列岛的实测数据,以潮流流速变化的一个半月周期内捕获总能量最大为目标,利用MATLAB计算迭代得到合适的设计流速。与最大潮流流速作为设计流速的设计方法作对比,对不同流速下桨叶的旋转角速度及捕获功率情况作理论预测对比。搭建实验平台进行实际测试,结果显示:基于合适设计流速下的桨叶设计在潮流流速变化的大部分时间段内功率捕获优于以往设计桨叶,在潮流流速变化的一个半月周期内捕获总能提高了约8%,验证了该设计方法的正确性与合理性,本结论对变流速中定桨距桨叶的设计具有一定参考价值。
水平轴;定桨距桨叶;设计流速;周期捕获总能量;桨叶性能对比
Abstract:Aiming at solving the key problem of fixed-pitch blade of tidal current turbine,a mathematical model for design velocity in variable flow velocities and blade capturing power is established using blade momentum and fluid dynamics theory.Based on the testing data around Jiushan archipelago and by maximizing the total capturing energy within a month and a half cycle of tidal current velocity variation as the goal,MATLAB is used to calculate iteration to get the right design velocity.Compared with the method of maximizing velocity as a design velocity,it makes a theoretical prediction on the angular velocity and the power captured of the turbine under different flow velocities.An experimental platform is set up for actual testing and the results show that the capturing power of the blade which is designed under appropriate design flow velocities is superior to that of the previous design blade during most time of marine current velocity variation,with the total capturing energy in a month and a half cycle of variable flow velocities increased by about 8%,validating the correctness and rationality of the design method,which has a certain reference value for the design of fixed-pitch marine current turbine blades in variable flow velocities.
Keywords:horizontal-axis;fixed-pitch blade;design flow velocity;cycle total energy captured;blade performance comparison
我国海岸线长,具有丰富的可再生潮流能资源,潮流能的开发利用对弥补能源短缺,缓解环境污染具有重要意义[1]。
桨叶是潮流能能量捕获的关键部件,其设计优劣直接关系到能量捕获效率的高低。英国MCT研制1.2MW首台具有偏航系统的潮流能捕获装置SeaGen,采用变桨距式水轮机可180范围内变桨,额定设计流速为2.25 m/s,能量利用功率系数高达0.45[2];意大利那不勒斯大学的GEM计划采用悬浮式叶轮,额定设计流速为2.7 m/s,额定功率为100 kW,于2011年在Venice附近测试,由于实验测试地点平均流速在1.5 m/s左右,其输出功率达到20 kW[3];爱尔兰公司Open Hydro则利用外环导流功能提高来流流速开发Open-Centre水轮机,已在Orkney岛成功并网发电[4];丹麦的Fuglsang等以桨叶发电的单位输出能量成本为目标多变量对叶片进行优化[5]。我国潮流能发展起步比较晚,浙江大学李伟等[6]采用变速运行的最优叶片设计方法设计叶片的几何特性,在实际海况下的设计流速附近功率系数达到0.341;王树杰利用柔性叶片实现变流速下最佳翼型变换和自变桨[7]。
定桨距桨叶结构简单,但由于潮流流速大小不停变化,其工作效率很长一段时间处于较低水平,导致捕获功率较小以及可利用时间有限不稳定的问题。因此,在变流速情况下,定桨距桨叶设计不应该仅仅考虑设计点附近的功率捕获。
1 潮流设计流速的选取分析
潮流能发电装置的电功率一般从切入流速v0开始产生有效功率,当达到设计流速vr附近桨叶捕获功率最理想。不同的设计流速得到不同的桨叶外形几何参数及不同的功率捕获情况。

图1 潮流流速中桨叶工作特性Fig.1 The blade working characteristics in variable velocity
目前,通常选取当地海域最大潮流流速均值作为桨叶设计流速,如图1所示,当潮流流速达到最高时的短短几个小时内,桨叶在设计点附近输出最大功率,当潮流流速较低时,桨叶的叶尖速比不再是最佳,效率下降。
定桨距桨叶设计不仅要满足考虑在设计点处最大功率输出,还要充分考虑非设计点的桨叶功率捕获情况。因此,要选取合适的设计流速,实现在潮流流速变化周期内实现最大能量捕获。
2 变流速中设计流速与桨叶捕获功率数学模型的建立
2.1变流速流经桨叶的轴向与切向流速变化
根据叶素动量理论[8],额定设计流速流经桨叶的流速变化值,即轴向诱导因子a是不受相邻径向位置的作用,为固定值。但对于设计流速为vr、安装角一定的定桨距桨叶,随着流速vt变化,流经桨叶的流速变化情况也不同,故引入轴向诱导因子at,该值随流速变化而变化,而瞬时值沿径向固定不变。如图2所示,桨叶在来流流速冲击下旋转,扫掠成一个圆盘,流经圆盘整体的流速在轴向速度改变为vt(1-at),且桨叶旋转的角速度为ωt,也随流速的变化而变化。同理,引入随流速变化的切向诱导因子bt,切向速度与径向位置r有关,则切向净流速为ωtr(1+bt)。
根据动量定义,切向诱导因子与轴向诱导因子之间的关系如下[9]:
式中:λ=ωtR/vt为叶尖速比,μ=r/R表示半径r处径向位置。

图2 流经桨叶流速变化Fig.2 The velocity change of blade
2.2变流速下桨叶叶素速度及受力分析
将叶片沿翼展方向分成若干微元,取r处进行分析。如图3所示,水流相对于桨叶叶素的合成来流速度Wt为[10]:
式中:φ=α+β为入流角(),α为桨叶攻角(),β为桨距角()。
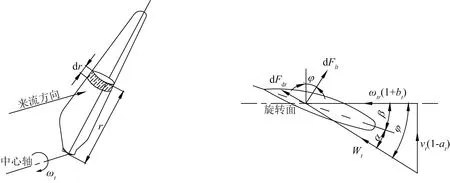
图3 叶素的速度和作用力Fig.3 Speed and force of the blade element
桨叶叶素翼型的升力dFlt、阻力dFld[11]为:
式中:ρ为海水密度(kg/m3),c为叶素翼型的弦长(mm),Clt、Cdt分别为叶素翼型升力系数与阻力系数。
根据动量定理,作用在叶轮(r,r+dr)环形域上的扭矩[9]也可以表示为:

将式(1)代入式(5)中得到:
2.3桨叶轴向诱导因子与设计流速的数学关系
式(1)忽略阻力的影响,根据式(6)得到桨叶单位展长的升力Flt在其旋转方向上分量为:
结合式(2)、式(3)和式(7)得任意t时刻流速流过该设计桨叶时的升力与设计流速t0时刻的升力大小之比为:
升力系数主要受攻角影响,定桨距桨叶攻角固定,故忽略流速变化对升力系数的影响,有:
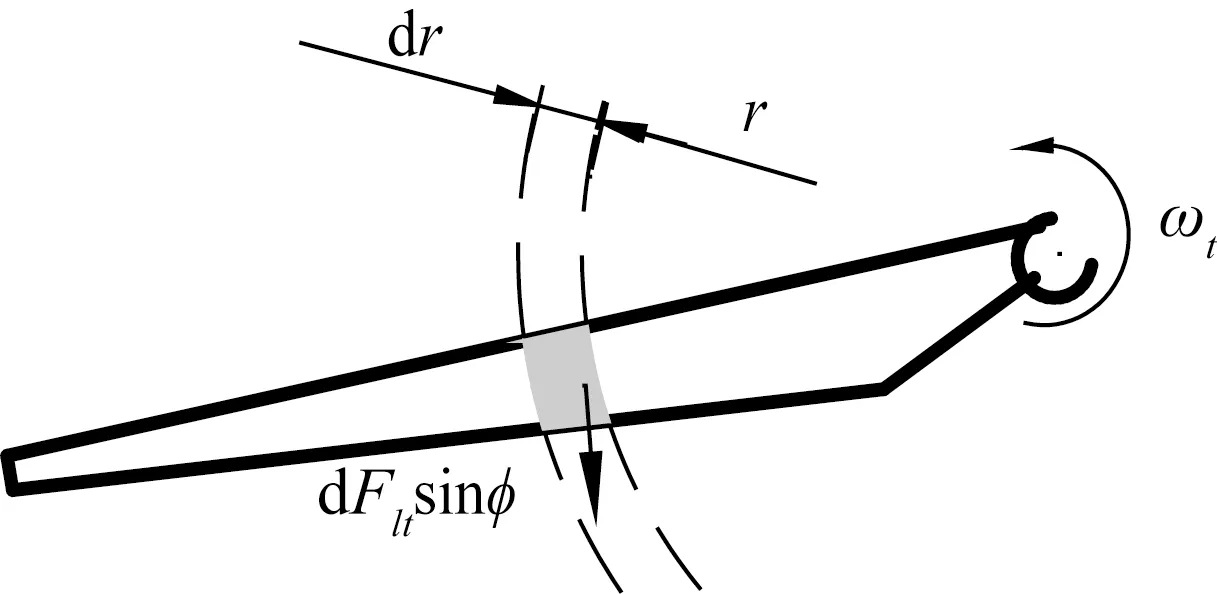
图4 桨叶旋转动能Fig.4 Blade rotational kinetic energy
式中:ωr为设计流速vr流经桨叶时的旋转角速度(rad/s),Flr为设计流速t0时刻的升力(N),ar为设计流速的轴向诱导因子。
从力学角度分析,桨叶绕定轴转动,动能Et为式(10);同时,桨叶微圆环在旋转面上受到的力矩为Mt=dFltsinφ·r,如图4所示,则在微小dt时间段内以ωt角速度旋转的动能也可用式(11)表示:

式中:Jb、Jh分别为该设计桨叶叶片与轮毂绕中心轴的转动惯量(kg·m2)。
结合式(2)、式(10)和式(11)得角速度ωt与角速度ωr之比为:
将式(12)代入式(9),得流速变化时的轴向诱导因子at与最佳设计状态下的诱导因子ar之间数学关系:
当vt=vr时,有at=ar,即当潮流流速达到设计流速时轴向诱导因子达到最佳运行时的轴向诱导因子。在潮流变化中选取不同的设计流速,轴向诱导因子会出现不同的变化规律。
2.4设计流速与桨叶捕获功率及功率利用系数之间的数学关系
根据动量理论,桨叶的功率利用系数与捕获功率分别为:
假设桨叶在设计流速vr下运行最优,根据贝茨理论,流速达到设计流速时,轴向理想诱导因子ar=0.333,代入式(14)和式(15),在t时刻桨叶的理想功率利用系数及其理想捕获功率为式(16)和式(17):

3 流速变化一个半月周期内的设计流速计算
在实验地点韭山列岛测量潮流流速,此处潮流属于正规半日潮,即一天内出现两次最强涨潮流速和两次最强落潮流速,且相邻的涨潮流速与落潮流速基本相等。每一小时测量一次,发现潮流的半日周期T约为12.42小时,最大潮流流速在2.2 m/s左右,小潮最大流速在0.8 m/s左右。图5所示为桨叶一个半月周期(约350小时)的涨潮流速。
利用MATLAB编程,依次取不同设计流速0.8,1.0,1.2…,计算变流速下功率并乘以Δh=1得到每小时的能量捕获,并叠加得到不同设计流速桨叶在一个半月周期中的总能量,如式(18)所示。其中,不考虑实际工作损耗,假设初始流速为v0=0 m/s;考虑实际工作损耗,假设v0=0.6 m/s开始有效工作。
取桨叶半径1.5 m,得到图6不同设计流速下桨叶的周期捕获总能量,可以看到:桨叶设计流速1.6 m/s的捕获总能最大,与取最大潮流流速2.2 m/s为设计流速的桨叶相比,本文设计流速下的桨叶理论捕获总能提高了3%,约30kW·h。并且在考虑负载阻力,即从 0.6 m/s开始计算求得设计流速仍为1.6 m/s,说明特别小的流速对整体的迭代计算无影响。
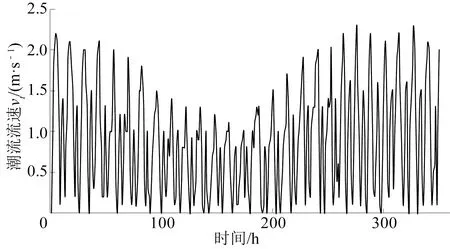
图5 一个半月周期潮流流速vtFig.5 Velocity in a cycle of one month and a half

图6 不同设计流速下桨叶的周期捕获总能Fig.6 Total-cycle energy captured with different design velocities
4 不同设计流速下桨叶外形参数及静态性能预测
将以往设计流速选取方法与本文设计流速下的桨叶进行外形参数计算并在这些参数基础上进行理论静态性能预测,分别取潮流平均最大流速2.2 m/s与计算值1.6 m/s为设计流速,对两种设计流速下的桨叶进行静态性能预测分析。
4.1不同设计流速下桨叶的外形参数
结合Wilson叶片优化设计理论,利用MATLAB优化工具箱中的非线性约束最优化函数fmincon可以快速求解两种桨叶外形尺寸[12]。
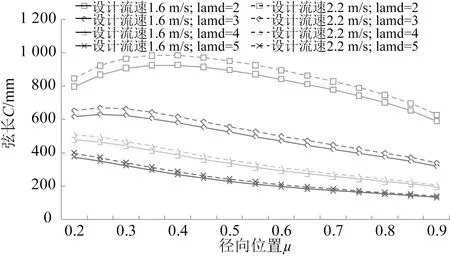
图7 桨叶的弦长Fig.7 The blade chord length
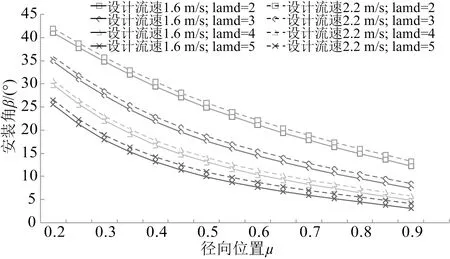
图8 桨叶的安装角Fig.8 The blade installation angle
图7为桨叶弦长,可以看到:在相同叶尖速比时,设计流速为1.6 m/s桨叶的弦长在径向各个位置均小于设计流速为2.2 m/s的桨叶;随着叶尖速比的增大,两种桨叶的弦长都随之减小,叶尖速比越大,弦长越小。图8为安装角,由于不同设计流速的选取,设计流速为1.6 m/s的桨叶安装角小于设计流速为2.2 m/s,前者可以减小轮毂安装尺寸。
4.2不同设计流速下桨叶的整体轴向诱导因子变化
根据式(13)得两种设计流速下桨叶随流速变化的轴向诱导因子,只有在设计流速附近桨叶的轴向诱导因子才接近理想值0.333,而当流速变化到远离桨叶设计流速点附近后,轴向诱导因子值也远离理想值。利用变流速下诱导因子变化进行定桨距桨叶静态性能分析。
4.3两种设计流速在不同叶尖速比下转速变化
结合图9与式(12)计算变流速时两种桨叶在不同叶尖速下角速度,如图10所示,可以看出:相同的设计叶尖速比下,设计流速1.6 m/s的桨叶角速度均大于设计流速为2.2 m/s的桨叶,说明理论上前者的启动性优于后者。
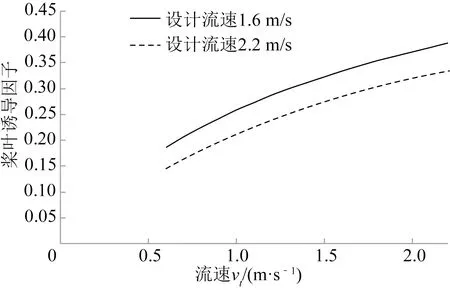
图9 变流速的轴向诱导因子变化Fig.9 Axial-induced factor change of variable velocity

图10 两种桨叶在不同叶尖速比下的理论转速Fig.10 Theoretical speed change of two different blades under different tip speed ratios
4.4捕获效率理论预测对比
在桨叶设计中功率捕获是最终验证桨叶设计优劣的关键参考。根据图10与式(7)得两种桨叶在不同设计叶尖速比下的功率捕获大小,从图11可以看出:随着叶尖速比的增大,桨叶理论捕获功率略微增大,但增大趋势不明显。其中:采用1.6 m/s设计的桨叶在大部分低流速下的理论功率捕获大于采用2.2 m/s设计的桨叶,只有在流速最大的附近前者小于后者。
图12为理论功率利用系数预测,可以看出:在不同的设计叶尖速比下,两种设计桨叶的功率利用系数变化规律与功率变化基本一致:当流速在0.6~1.8 m/s附近,设计流速为1.6 m/s的桨叶功率利用大于设计流速为2.2 m/s的桨叶;在流速为1.9~2.2 m/s左右流速变化时,后者大于前者。
总之,选取设计流速为1.6 m/s进行桨叶设计,从理论上分析桨叶在大部分低流速段功率大于其对比桨叶,启动性更好优先到达设计点附近。
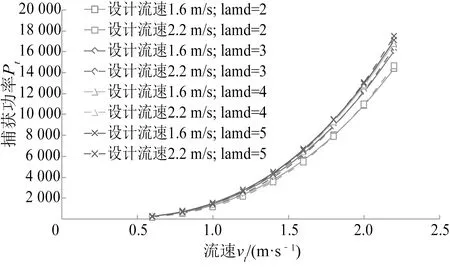
图11 桨叶在不同流速下的捕获效率对比Fig.11 Contrast of blade capture efficiencies under different velocities

图12 不同设计流速的桨叶在不同叶尖速比下的效率捕获Fig.12 Capture efficiency of the blade with different velocities under different tip speed ratios
5 实验验证桨叶效率捕获情况
5.1桨叶设计加工
根据静态性能预测,叶尖速比为3时桨叶功率捕获、转速及扭矩都比较理想;翼型选取选择NACA63-4xx系列[13],该翼形在风力机中的大量应用已证明其具有较好的失速特性。表1为两种桨叶的整体设计参数。

表1 两种桨叶整体设计参数Tab.1 Overall design parameters of two kinds of blades
实际桨叶采用三叶片形式,采用玻璃钢材料制成,强度高、重量轻、耐老化,轮毂采用高强度球墨铸铁,力学性能好、易成形、成本低。图13为两种桨叶实物图,桨叶B径向各个位置均大于桨叶A,密实度大。

图13 两种加工的桨叶实物对比Fig.13 Physical contrast pictures of the two blades

图14 海上实验平台Fig.14 The experiment platform on the sea
5.2实验平台搭建及实验数据采集
1)海上实验平台搭建
在海水测试地点进行实际潮流能捕获性能测试,图14为潮流捕获与发电系统的综合海上实验平台。将图11中两桨叶先后固定,当潮流速度提高至潮流能捕获叶轮的启动转速时,叶轮便开始转动,通过增速传动机构将转速提高后带动永磁发电机工作。同时,电量采集模块实时将采集到的数据返回;当检测到有电压数据时,PLC通过控制固态继电器来自动进行负载的匹配,同时测试信号通过A/D转换模块传送至PLC控制器进行处理,实时传送至上位计算机进行记录保存。
2)将海上实验平台实际测试数据记录并整理,与理论预测对比分析。
为方便观察两种桨叶实际性能,将数据整理,其中图15为两种桨叶随流速逐渐增大的实际转速,明显看出:桨叶A在低流速阶段启动且转速大于桨叶B,但两种桨叶在流速2 m/s附近由于存在失速转速均降低,由于桨叶B接近其设计点附近,因此桨叶A明显小于桨叶B。此外,桨叶A在流速1.8 m/s附近转速达到最大,估计存在失速延迟问题[14]。图16分别为两种桨叶实际叶尖速比测量值,桨叶A在大部分流速下均接近设计叶尖速比3,而桨叶B由于其密实度较大,涡流损耗严重,没有桨叶A运行理想。
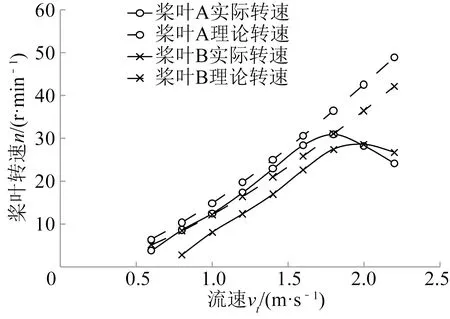
图15 桨叶转速测试Fig.15 The blades speed test
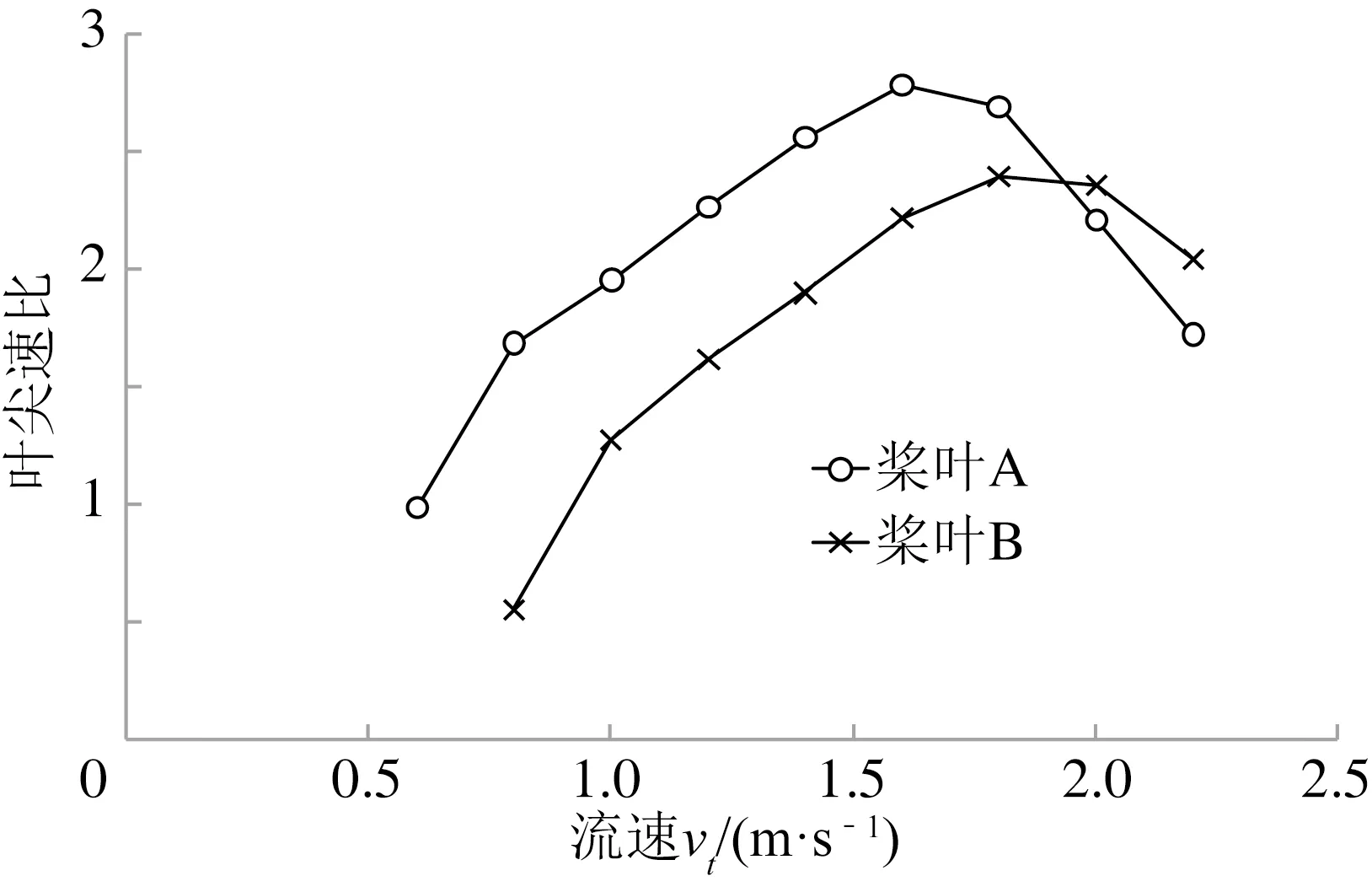
图16 桨叶实际叶尖速比值Fig.16 The actual values of the blade tip speed ratio
图17为两种桨叶在流速实际测试变化的一个半月周期内功率捕获情况(流速数据如图5所示),通过海上测试平台直接记录数据。桨叶A在大部分低流速时间段内功率捕获大于桨叶B,只有在流速很大的时候后者的功率优于前者。桨叶A、B的实际捕获总能分别为理论预测值的66.8%和63.7%,前者的实际增量是后者的约8%,高于理论增量率,考虑为前者存在失速延迟,后者密实度大涡流明显能量损失导致捕获能量小于其理论计算。进而试验验证本文理论及设计方法的合理性。
图18为一个半月周期内实际潮流流速测试中桨叶实际功率利用系数,可以看出:桨叶A功率利用系数基本大于桨叶B,最大接近0.36;桨叶B的最大功率利用系数接近0.32。
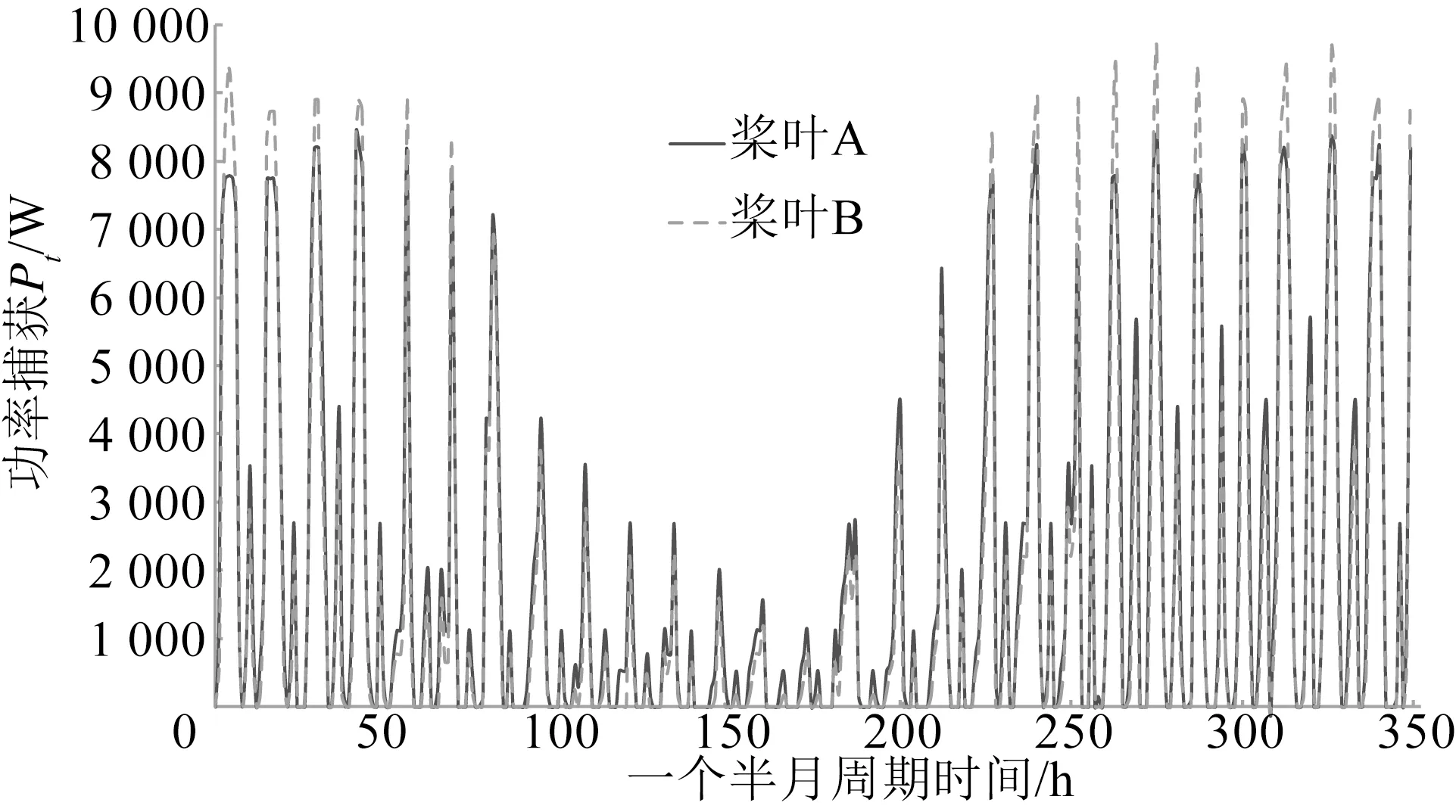
图17 一个半月周期内桨叶功率捕获测试Fig.17 Blade power utilization coefficiency test in a cycle of one month and a half
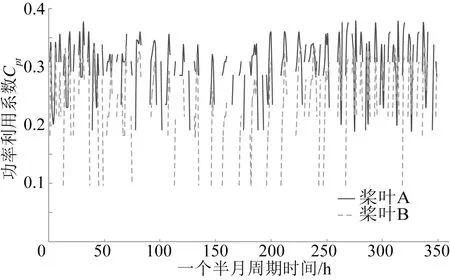
图18 一个半月周期中桨叶功率利用系数测试Fig.18 Blade power capturing test in a cycle of one month and a half
桨叶A在大部分流速时段的运行性能优于桨叶B,由于实际潮流流速出现最大潮流流速时间段很短。因此,桨叶A在流速变化一个半月周期内捕获总能大于桨叶B。实际运转中桨叶B密实度较大,失速问题造成了捕获能量与理论值相比低于设计桨叶A。结果与理论预测基本一致。
由于实验环境限制,本文所取桨叶半径不大,周期内捕获能增加量比较小,随着半径增大,周期内能量捕获成二次方增长。
6 结 语
1)建立了变流速下定桨距桨叶的设计流速与功率捕获数学模型,并结合实际潮流流速变化,以流速变化一个半月周期内桨叶捕获总能量最大为目标,迭代计算合适的设计流速。
2)将1.6 m/s设计流速的桨叶与最大潮流流速2.2m/s设计流速的桨叶转速和功率及功率利用系数进行理论预测,最后通过实际测试,验证本文设计桨叶性能优于以往最大设计流速的设计桨叶。
3)由于忽略阻力负载,与实际桨叶工作性能有一定的差距,需要进一步修正。同时,对于实际运行中存在的失速延迟及失速问题应进一步研究分析。
[1] FRA EN KEL P.Tidal current energy technologies[J] .International Journal of Avian Science,2006,148(4):145-151.
[2] A S Bahaj,W M J Batten,G McCann.Experimental verifications of numerical predictions for hydrodynamic performance of horizontal axis marine current turbines [J].Renewable Energy,2007,32(1):2479-2490.
[3] 张亮,李新仲,耿敬,等.潮流能研究现状2013[J].新能源进展,2013,1(1):53-68.(ZHANG Liang,LI Xinzhong,GENG Jing,et al.Tidal current energy update 2013[J].Advances in New and Renewable Energy,2013,1(1):53-68.(in Chinese))
[4] ALESSANDRO Schanborn.Development of a hydraulic control mechanism for cyclic pitch marine current turbines[J].Renewable Energy,2007,32:662-679.
[5] FUGLSANG P,MADSEN H A.Optimization method for wind turbine rotors [J].Journal of Wind Engineering and Industrial Aerodynamics,1999,80(1-2):191-206.
[6] 徐全坤,李伟,刘宏伟,等.水平轴潮流能发电机组独立变桨距系统[J].浙江大学学报(工学版),2013,47(3):528-534.(XU Quankun,LI Wei,LIU Hongwei,et al.Individual blade pitching system for horizontal axis tidal current turbine[J].Journal of Zhejiang University(Engineering Science),2013,47(3):528-534.(in Chinese))
[7] 王树杰,李冬,赵龙武,等.柔性叶片水流发电模型试验研究[J].太阳能学报,2010,31(3):362-366.(WANG Shujie,LI Long,ZHAO Wulong,et al.Experimental research on current energy model with flexible vanes[J].Acta Energiae Solaris Sinica,2010,31(3):362-366.(in Chinese))
[8] LANZAFAME R,MESSINA M.Dynamics wind turbine design:critical analysis,optimization and application of BEM theory[J].Renewable Energy,2007,32:2291-2305.
[9] TONY Burton,DAVID Sharpe,NICK Jenkins,et al.Wind energy handbook[M].John Wiley &Sons Ltd,2005.
[10] BALAKA R,RACHMAN A.Pitch angle effect for horizontal axis river current turbine[J].Procedia Engineering,2012,50:343-353.
[11] GROGAN D M,LEEN S B,KENNEDY C R,et al.Design of composite tidal turbine blades[J].Renewable Energy,2013,57:151-162.
[12] 李国宁,杨福增,杜白石,等.基于MATLAB与Pro/E的风力机叶轮设计及造型[J].机械设计,2009,26(6):3-5.(LI Guoning,YANG Fuzeng,DU Baishi,et al.Design and modeling of wind wheel of wind mill based on MATLAB and Pro/E[J].Journal of Machine Design,2009,26(6):3-5.(in Chinese))
[13] PRATUMNOPHARAT,LEUNG P S.Validation of various wind mill brake state models used by blade element momentum calculation[J].Renewable Energy,2011,36(11):3222-3227.
[14] 戴韧,王海刚.水平轴风力机失速延迟特性及其力学机理的研究[J].太阳能学报,2008,29(3):337-342.(DAI Ren,WANG Haigang.Predicting stall delayed performance of rotating hawt and its inherent mechanical driving forces[J].Acta Energiae Solaris Sinica,2008,29(3):337-342.(in Chinese))
Research on the design flow velocity of blade of horizontal axis tidal current turbine
LIN Zuan1,2,ZHANG Li3,LI Jianghua3,JIANG Chuhua2,CHEN Junhua2,YANG Canjun1
(1.School of Mechanical Engineering,Zhejiang University,Hangzhou 310027,China; 2.Ningbo Institute of Technology,Zhejiang University,Ningbo 315100,China; 3.School of Mechanical Engineering Taiyuan University of Science and Technology,Taiyuan 030024,China )
P742
A
10.16483/j.issn.1005-9865.2016.02.010
1005-9865(2016)02-0071-09
2015-03-23
国家海洋局可再生能源专项资金资助项目(NBME2011CL02);宁波市民生科技资助项目(2013C11037)
林 躜(1978-),男,武汉人,讲师,从事海洋能利用、机电测控等研究。E-mail:lzuan@nit.zju.edu.cn
杨灿军。ycj@zju.edu.cn
