多扰动电能质量检测方法的研究

徐　健　吴飞飞

(西安工程大学电信学院，陕西 西安　710048)



多扰动电能质量检测方法的研究

徐健吴飞飞

(西安工程大学电信学院，陕西 西安710048)

针对电能质量中扰动类型复杂、频率成分不确定的特点，采用改进希尔伯特-黄变换(HHT)和广义S变换相结合的方法进行检测。选取谐波和电压暂降的混合扰动作为目标信号，采用改进的HHT进行集合经验模态分解(EEMD)，提取各频率成分即得到固有模态函数集合(IMF),确定基本组成；将各层IMF进行快速改进S变换(广义S变换)，得到精确信息。试验结果表明，HHT和广义S变换相结合的方法所测得的多扰动电能检测精度更高。

电能质量多扰动谐波电压暂降改进HHT广义S变换EEDMIMF

0　引言

电能质量可以简单地分为稳态电能质量和暂态电能质量[1]。稳态电能质量(如电压波动与闪变、谐波、三相不平衡)，主要检测的是波动幅值、不平衡因子、出现频率等特性[2]；暂态电能质量(如脉冲震荡、电压暂升、电压暂降、电压中断[3])，主要检测的是峰值、频谱、起止时刻、持续时间等特性。在现实生活中，出现的电能质量往往不是单一形式的，而是两种甚至多种电能质量的混合[4]，并且还混有噪声等影响因素。电压暂降和谐波的混合是较为典型的混合扰动。

电能扰动检测的方法很多，如傅里叶变换、短时傅里叶变换、dq变换、小波变换等[5]。S变换和希尔伯特-黄变换(Hilbert-Huangtransform,HHT)是两种比较新的时频算法，在处理非平稳、非线性信号时，检测结果更为准确[6-8]。S变换的窗宽和面积完全可调。文献[9]通过比较S变换与短时傅里叶变换对电压暂降的检测结果，阐述了S变换处理暂态扰动信号的优势。HHT是小波变换的发展，具有自适应性。文献[10]通过比较HHT与小波变换对谐波的检测结果，阐述了HHT处理稳态扰动信号的优势。基于此，将HHT和S变换有效结合，便可对电能中任何扰动信号进行准确识别。为了提高检测精度，先分别对S变换和HHT进行改进，然后再将这两种变换相结合，并应用于电压暂降与谐波的混合扰动中。

1　算法及其改进原理概述

1.1S变换及其改进

1.1.1S变换

信号h(t)的S变换定义为[11]：

S(τ,f)=∫-∞∞h(t)g(τ-t)e-2πftdt

(1)

(2)

式中：f为频率；τ为控制高斯窗口在时间轴位置的参数；h(t)为原始信号。

高斯窗的大小与频率成反比，即在低频段仍具有较高的频率分辨率和较低的时间分辨率。这为下面的改进提供了理论基础[9]。

1.1.2S变换的改进

电压暂降类型的扰动信号，在低频时对时间分辨率要求较高；而单纯的S变换虽然较以往的时频检测方法有所改进，但依然存在一定误差，故引进频率调节系数f=αf+β。通过调节α和β，便可使广义S变换在不同时频面上具有不同的分辨率。

改进的高斯窗函数如下：

(3)

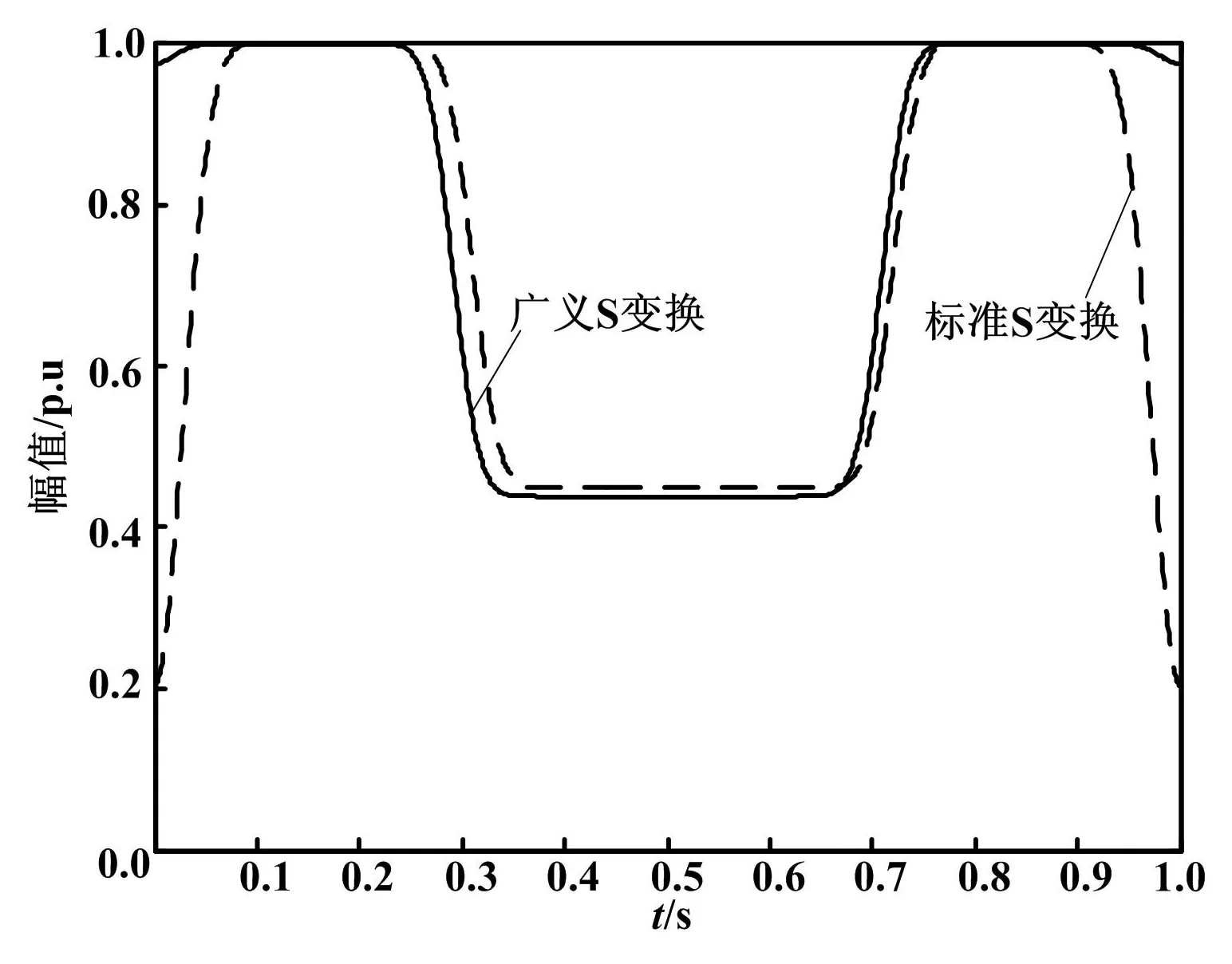
图1　基频曲线

S变换和广义S变换的误差比较如表1所示。

表1　两种算法的误差比较

1.2HHT及其改进

1.2.1HHT

HHT是小波变换的改进与发展，具有自适应性。其组成原理可分为两部分：经验模态分解(empiricalmodedecomposition,EMD)、希尔伯特变换。EMD的具体过程介绍如下[13]。

①找出信号x(t)所有的极大、极小值点作为上包络线v1(t)和下包络线v2(t)，并求其平均值m1(t)：

(4)

②对信号x(t)与平均值m1(t)作差，得：

h1(t)=x(t)-m1(t)

(5)

③将h1(t)作为原始信号，重复步骤①和②,依次得到各阶固有模态函数(IMF)分量，直到满足给定的终止条件时筛选结束。分解表达式如下：

(6)

1.2.2HHT的改进

当存在多种频率成分时，EMD分解可能出现模态混叠现象。文献[14]提出了集合经验模态分解(ensembleempiricalmodedecomposition,EEMD)方法。在分解过程中加入白噪声，由于噪声的存在，使得新的分解结果较EMD的分解结果复杂，此时系统就会产生足够多的测试值均值，以消除噪声。多次测试所得到的均值会被认为是信号分解的最终结果。

EEMD解决了EMD的模态混叠问题，经过EEMD后再进行希尔伯特变换，处理结果更精确。

1.3两种改进算法的嵌套应用

对于谐波和电压暂降之类的暂态与稳态相结合的混合扰动，由于特征不同，单采用一种算法，必然会存在顾此失彼的现象。将改进HHT和广义S变换相结合，取长补短，可进一步提高检测精度。

利用改进后的HHT进行EEMD处理，提取混合信号的固有模态函数(intrinsicmodefunction,IMF)成分，将各层IMF进行快速改进S变换，提取每一层的特征，对输入信号进行详细分析。

算法应用流程图如图2所示。

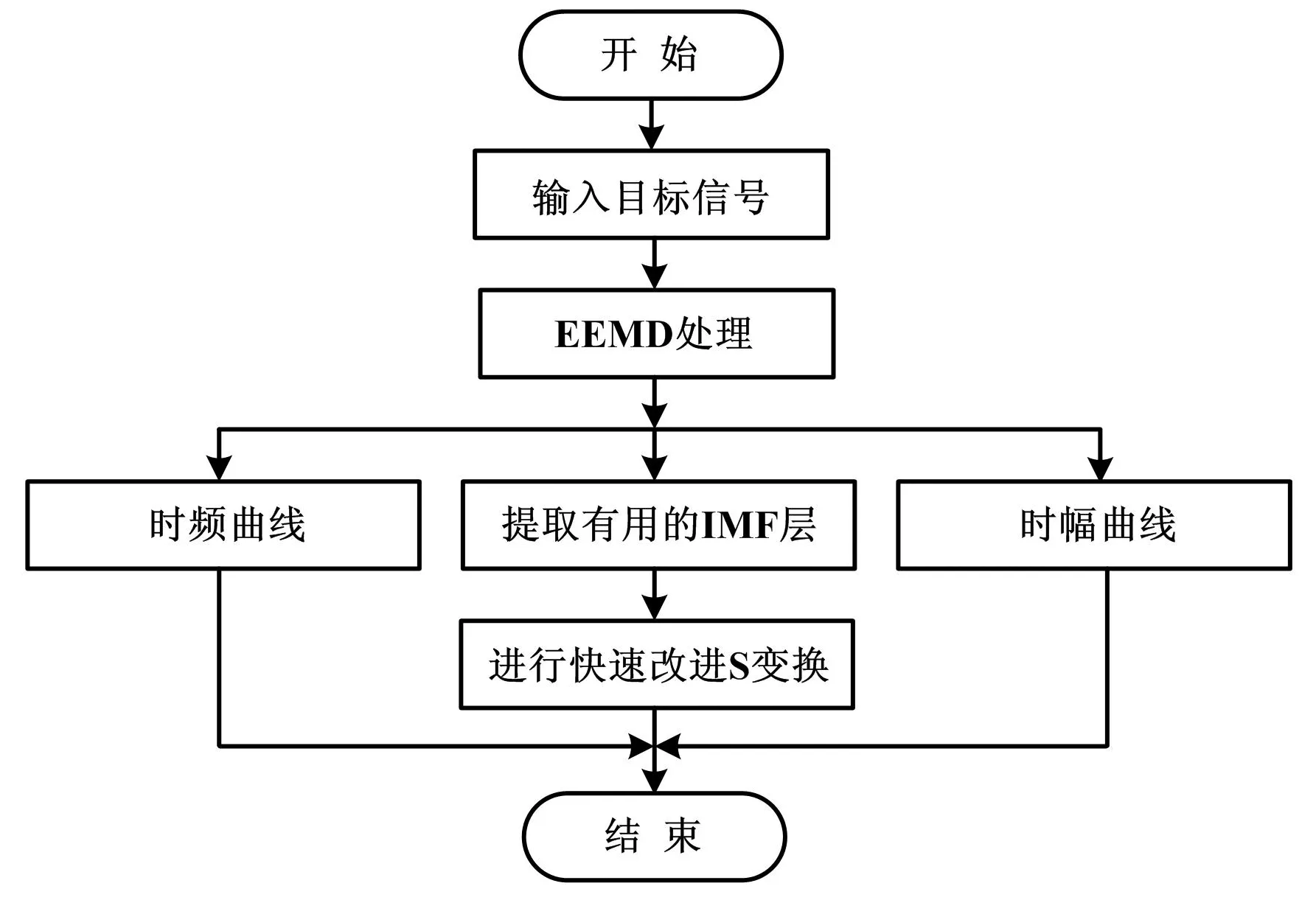
图2　算法应用流程图

2　仿真验证

目标信号如图3所示。对扰动信号进行EEMD，如图4所示。

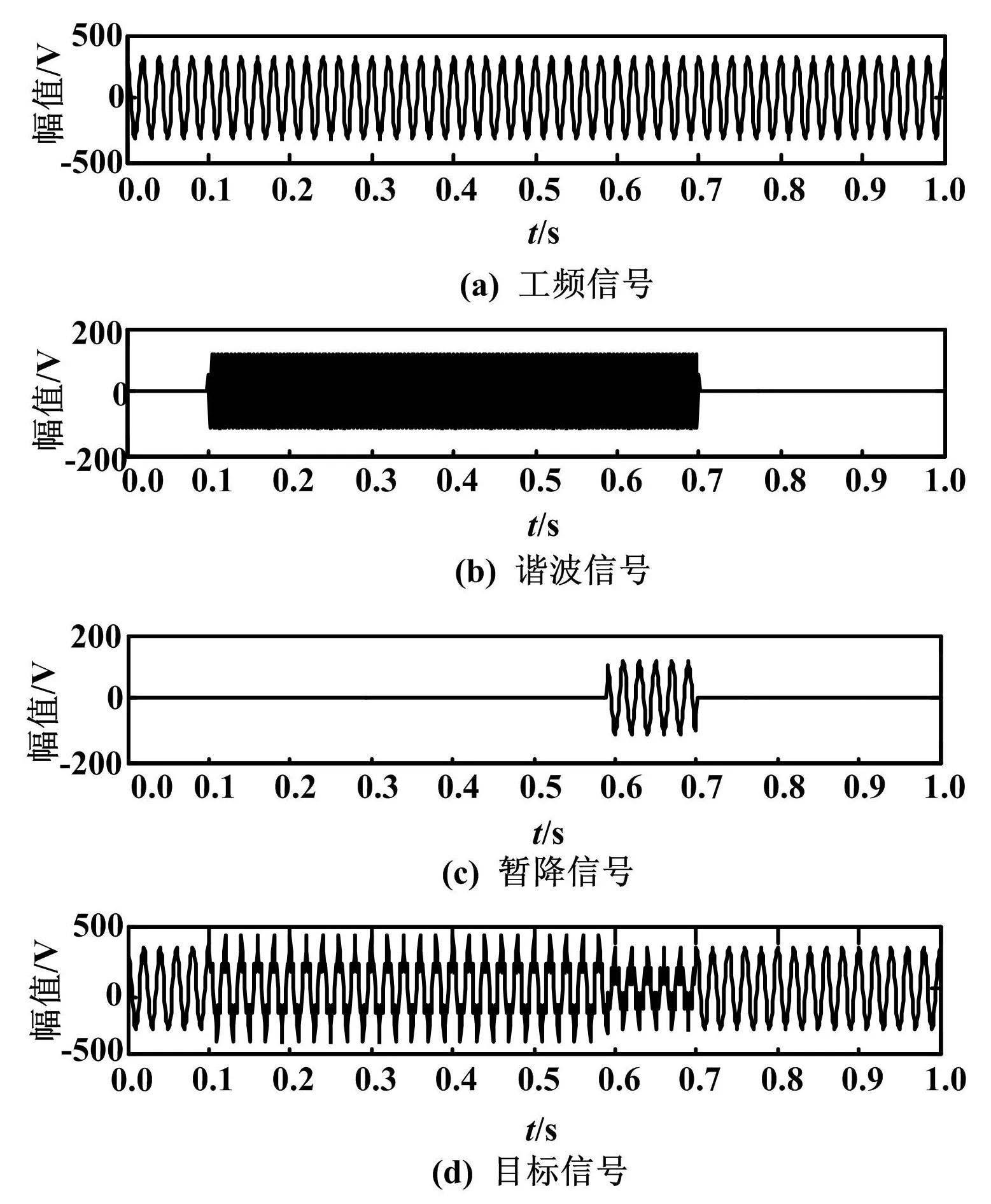
图3　扰动信号

图4　EEMD示意图

左半部分是各层IMF的时频曲线，右半部分是相对应各层IMF的幅频分布。从各层IMF时频图可知，IMF1中包含250Hz和50Hz两种频率成分，250Hz的谐波信号出现在0.1～0.7s间。由频谱图可知，IMF1的主要信号成分为谐波和暂降，而无工频信号；IMF2中只存在50Hz的信号，其出现时间段为0.1～0.7s,又由对应幅值可知其主要成分为暂降信号，且在0.6～0.7s

发生突变；IMF3和IMF4属于无关信号。因此只需对IMF1和IMF2进行S变换处理，即可提取更精确的信息。

目标信号HHT特性曲线如图5所示。快速广义S变换处理后的幅值包络图如图6所示。

图5　目标信号特性曲线

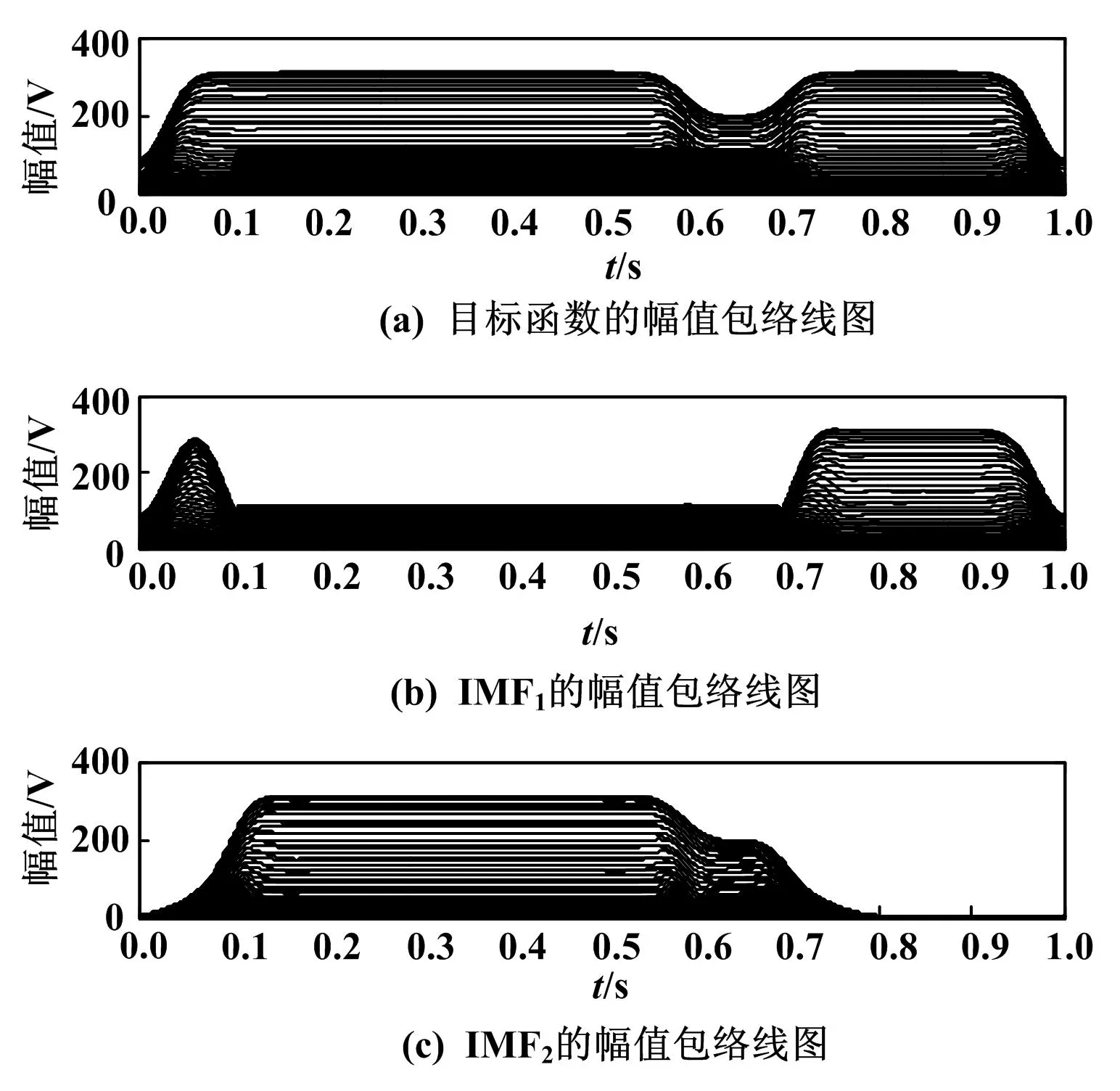
图6　相关信号的幅值包络图

图6(a)能基本反映原始信号的成分，但由于信号较复杂(含有工频成分)，对检测结果产生了干扰，不够精确。由图6(b)可知，在0.1～0.7s，只检测到扰动信号而无工频信号的影响，对于谐波的检测结果必然更加精确。图6(c)中无谐波信号的干扰，只检测到电压暂降信号。为了更直观地说明问题，提取变换过程中的数据，如表2、表3所示。各层IMF进行S变换后的时间定位、幅值检测误差较小，精确度高。

表2　时间检测结果分析

表3　幅值检测结果分析

表2、表3中：IMF1、IMF2误差较目标函数误差小，即经过EEMD分解后再进行广义S变换，由于滤除了不需要的杂质信号，其精度变高。检测结果证明了两种算法结合的可靠性与有效性。

3　结束语

结合电能质量中的多扰动特征，应用了改进HHT与快速广义S变换相结合的算法。改进后的EEMD和S变换在检测精度上都有了提高。对多扰动中的典型代表谐波与电压暂降的混合进行仿真，利用改进HHT进行分解，提取频率成分，进行整体分析；广义S变换对HHT的结果进行精确分析，确定幅值、突变起止时刻信息。仿真试验表明，两种改进算法的结合能有效提取多扰动的各方面信息，精度较单一算法更高。

[1]YUANS,HUANGRC,TONGW,etal.VoltageflickermeasurementbasedonDSPplatformanditserrorcorrection[J].ThePowerSystemProtectionandControl,2008,21(4): 47-51.

[2] 程浩忠.电能质量介绍[M] ．北京：中国电力出版社，2008．

[3] 程浩志,吕干云,周荔丹.电能质量监测与分析[M].北京：北京科学出版社，2012：28 -33.

[4] 尹柏强,何怡刚,朱彦卿.一种广义S变换及模糊SOM网络的电能质量多扰动检测和识别方法[J].电机工程学报,2015,4(35):866-872.

[5] 吕干云,冯华君,牛更军,等.基于S变换的电力系统间谐波检测[J].仪器仪表学报，2006,27(6):1676-1682.

[6] 唐求，滕召胜，高云鹏，等.基于S变换的平方检测法测量电压闪变[J].中国电机工程学报，2012，32(7)：60-67.

[7] 周林,吴红春,梦婧,等.电压暂降分析方法研究[J].高电压技术,2008,5(34):1011-1015.

[8] 刘云潺,王建鹏.HHT在电压暂降检测中的应用[J].科技创新导报,2009(28):51-53.

[9] 徐健,张宇勍,李彦斌,等.短时傅里叶变换和S变换用于检测电压暂降的对比研究[J].电力系统保护与控制,2014,42(24):44-48.

[10]程思勇.小波与HHT在电能质量分析中的应用[D].吉林:东北电力大学,2007.

[11]易吉良,彭建春,谭会生.S变换在电能质量扰动分析中的应用综述[J].电力系统保护与控制,2011,39(3):141-146.

[12]郑曙光，刘观起.基于广义双曲S变换的快速谐波检测算法[J].电测与仪表,2015,52(9):30-35.

[13]李天云,高磊,赵妍.基于HH丁的电力系统低频振荡分析[J].中国电机工程学报,2006,14(26):24-29.

[14]朱宁辉,白晓民,董伟杰.基于EEMD的谐波检测方法[J].中国电机工程学报,2013,33(7):92-97.

ResearchontheDetectionMethodofMulti-disturbancePowerQualityDetection

Inviewofthecomplexcharacteristicsofthedisturbancetypesandtheuncertainfrequencycomponentsinpowerquality,thecombinedmethodofimprovedHilbert-Huangtransform(HHT)andgeneralizedStransformareusedfordetection.Themixeddisturbanceofharmonicandvoltagesagareselectedasthetargetsignal,theensembleempiricalmodedecomposition(EEMD)isconductedbyusingHHT,toextracteachfrequencycomponent,andtogetintrinsicmodefunction(IMF)set,anddeterminethebasiccomponent.EachlayeroftheIMFisproceedfastimprovedStransform(generalizedStransform)todeterminethepreciseinformation.Thetestresultshowthatthecombinationoftwoalgorithmsbringsmoreaccuratedetectionofmeasuredpowerqualityundermultipledisturbances.

PowerqualityMulti-disturbanceHarmonicVoltagesagImprovedHHTGeneralizedStransformEnsembleempiricalmodedecomposition(EEDM)Intrinsicmodefunction(IMF)

徐健(1963—)，男，1986年毕业于西安工程大学自动化专业，获学士学位，副教授；主要从事电能质量监测方向的研究。

TH-3;TP273

ADOI:10.16086/j.cnki.issn1000-0380.201609016

修改稿收到日期：2016-03-09。