搜寻者优化算法与卡尔曼滤波相结合的PID控制
2016-10-12刘俊
刘 俊
(商洛学院电子信息与电气工程学院,陕西 商洛 726000)
搜寻者优化算法与卡尔曼滤波相结合的PID控制
刘俊
(商洛学院电子信息与电气工程学院,陕西 商洛726000)
针对传统PID控制器的参数整定依靠经验调整,且在控制过程中,系统易受多种噪声影响的问题,提出搜寻者优化算法与卡尔曼滤波相结合的PID控制方法。利用搜寻者优化算法对PID参数进行智能优化,利用卡尔曼滤波器实现对控制噪声和测量噪声的有效抑制。对二阶延迟系统进行仿真试验,结果表明,与传统PID控制方法相比,该方法可以智能地获得较优的PID参数,有效剔除了控制过程中的噪声干扰,实现了调节速度快、稳态误差低、抗干扰能力强的智能PID控制。
卡尔曼滤波器控制系统智能算法搜寻者优化算法PID控制参数整定噪声干扰信号
0 引言
在生产过程控制中,PID控制是应用较广泛的调节控制方法。然而,PID参数自适应整定一直是PID控制中一个至关重要的问题[1]。
随着智能算法和模糊神经网络的发展,一些学者对传统PID控制策略进行了改进和优化。文献[2]采用Smith模糊PID控制算法,解决了一阶线性纯滞后问题,加快了系统调节过程。文献[3]利用人工蜂群算法,对PID控制参数进行自适应整定。谢攀[4]等通过把传递函数时滞指数项近似有理化后,再利用全空间搜索法优化极点、频率和阻尼比等参数,间接得到PID参数,算法较简单,但对大时滞系统的控制能力较差。刘晴[5]、邓丽[6]、孙莉[7]等分别采用BP神经网络、免疫算法和模糊控制算法,通过优化PID参数进行系统控制,但这些方法在一定程度上,仍存在收敛速度慢、易陷入局部极值的缺点。
在生产过程中,系统经常受到非平稳随机噪声的影响,因此,本文使用全局寻优能力非常强的搜寻者优化算法(seeker optimization algorithm, SOA)和卡尔曼(Kalman)滤波器相结合的PID控制方法。该方法既实现了PID参数全局自适应优化,又有效抑制了控制噪声和测量噪声。
1 卡尔曼滤波器原理
卡尔曼滤波理论是由卡尔曼在1961年提出的[8],其利用状态空间概念描述系统,以最小均方误差为准则,通过递归算法获得最优线性估计状态解。在滤波过程中,卡尔曼滤波器只需要最近两次滤波数据,所以存储数据少、效率高、可靠性强,可用于多维平稳和非平稳噪声滤波处理[9]。卡尔曼滤波器结构如图1所示。

图1 卡尔曼滤波器结构示意图
对于离散时域系统,构建卡尔曼滤波器模型,得到的状态方程和测量方程分别为:
x(k)=Ax(k-1)+B[u(k)+ω(k)]
(1)
yv(k)=Cx(k)+v(k)
(2)
式中:x(k)为系统k时刻的状态量;A、B为转移矩阵参数;w(k)为k时刻的控制噪声;u(k)为k时刻的系统控制量;yv(k)为k时刻的测量值;C为测量矩阵参数;v(k)为k时刻的测量噪声信号。控制噪声和测量噪声是不相关的均值为零的高斯白噪声。
卡尔曼滤波器根据测量矩阵、转移矩阵、测量值和测量噪声协方差等数据,递推得到当前最优估计值。
离散卡尔曼滤波器的递推算法公式归纳如下[10]。
①状态估计协方差:
p(k)=A(k)P(k-1)A(k)T+BQBT
(3)
②滤波器增益:
M(k)=p(k)CT[Cp(k)CT+R]-1
(4)
③均方误差协方差:
P(k)=[I-M(k)C]p(k)
(5)
④状态估计值:
x(k)=Ax(k-1)+M(k)[yv(k)-
CAx(k-1)]
(6)
⑤滤波后输出值:
ye(k)=Cx(k)
(7)
以上公式中:I为单位矩阵;Q为控制噪声协方差;R为测量噪声协方差。
2 SOA算法优化PID控制器参数
2.1搜寻者优化算法
搜寻者优化算法(SOA)是一种群体智能搜索算法,由戴朝华等学者提出[11]。SOA算法模拟人类的智能搜索行为,能够通过有效描述自然语言和不确定性推理的模糊逻辑对搜索规则进行建模。SOA算法以搜寻者位置为个体,搜寻团队为种群,根据不确定推理确定个体前进的步长,根据经验梯度确定个体的搜索方向,通过不断更新个体位置,以获得问题的最优解。
2.2SOA算法优化PID控制器参数步骤
为了迅速、准确地进行PID控制器参数整定,使系统具有良好的鲁棒性和较快的收敛性,本文用搜寻者优化算法对控制器参数进行优化,具体优化步骤如下。
①初始化种群。
设种群有N个搜寻者个体,每个个体的位置矢量由PID控制器的比例、积分和微分三个控制参数组成,所以个体位置矢量的维数D=3。第i维参数的取值范围可根据实际工程应用背景统一或单独选取,对应的参数可在取值范围内随机选取。初始化种群可以用一个N×D的矩阵表示:
(8)
式中:POP为种群;KN为第N个搜寻者个体;knp、kni和knd分别为第n个搜寻者个体位置矢量中的比例、积分和微分参数。
②选取适应度函数,并计算每个搜寻者个体的适应度值。
在初始解向最优解进化的过程中,SOA算法仅通过适应度值来评价搜寻者个体的优劣。适应度值是个体更新的依据,用于指导个体不断在全局位置空间搜索,最后进化得到全局最优解。
为了获得PID控制过程误差特性,选取适应度函数为:

(9)
式中:e(t)为PID控制系统期望输出值r(t)与实际输出y(t)之间的误差,e(t)=r(t)-y(t);u(t)为PID控制器的输出;β1和β2为[0,1]之间的权值常数。

(10)
式中:权值β3≥100。
③确定群体中每个搜寻者个体的比例、积分和微分参数的搜索方向及步长。
SOA算法模拟人类的智能搜索行为,利用人类搜索经验梯度和模糊推理的行为,制定概念明确、易于理解、便于实现的搜索规则,从而确定搜寻者个体的进化方向和步长。
SOA算法的搜索规则可以简单归纳为:如果适应度值小,则步长短。可以理解为:当适应度值较小时,该搜寻者个体所处位置较优,更优位置可能在较优位置附近,所以应减小步长;当适应度值较大时,该搜寻者个体所处位置较差,则应该在更大范围内搜索,所以应增大步长。
搜寻者个体的实际搜索方向是综合多个经验方向、经加权几何平均确定的,包括向个体历史最佳位置前进的利己方向、向邻域最佳位置前进的利他方向和实时跟踪搜索效果的预动方向。搜寻者个体的搜索方向和步长的具体函数见文献[12]。
④更新搜寻者个体中比例、积分和微分的参数值。
搜寻者个体比例、积分和微分参数的更新函数如下:
(11)
式中:αnp(s)、αni(s)和αnd(s)分别为群体进化第s代时,第n个个体的比例P、积分I和微分D的搜索步长,{αnp(s),αni(s),αnd(s)}≥0;dnp(s)、dni(s)和dnd(s)分别为对应参数的搜索方向,且取值只能为-1、0和1,d(s)=1表示更新后的PID参数值增大,d(s)=0表示更新后的PID参数值保持不变,d(s)=-1表示更新后的PID参数值减小。
⑤判断终止条件。
如果满足终止条件,则停止搜索,并输出最佳PID控制器参数;否则,转至步骤②。
3 基于SOA算法和卡尔曼滤波器的PID控制
为了解决PID控制器参数整定的非智能性,减小传统PID控制过程中多维非平稳随机噪声的影响,提出基于SOA算法和卡尔曼滤波器的PID控制方法。控制系统通过SOA算法优化PID控制器参数,实现了PID控制器参数整定的智能化,并采用卡尔曼滤波器消除控制噪声和测量噪声,最终使系统误差减小、收敛加速、稳定性增强。控制系统结构如图2所示。

图2 控制系统结构图
控制系统按功能可以分为PID控制、噪声消除和PID控制参数优化三部分。
系统控制的实现过程是:①初始化搜寻种群(多组PID控制器参数),将种群中的个体(一组PID控制器参数)依次赋给PID控制器;对被控对象进行控制,并利用卡尔曼滤波器进行噪声消除处理,得到系统滤波后输出信号ye。②利用输出偏差e、PID控制律u和输出信号ye,计算得到每个个体的适应度值。③根据适应度值,利用SOA算法进行搜寻种群的更新,然后把更新后的个体继续代入PID控制器进行控制。④通过不断循环控制和PID控制参数的更新,直到满足循环条件(一般为循环次数或系统控制精度),则输出最优个体。⑤将最优PID控制器参数值代入控制器,并结合卡尔曼滤波器,即可得到控制系统的最佳输出值。
4 仿真研究
选取二阶延迟被控对象,其传递函数为:
(12)
设定采样时间为1ms,对传递函数进行离散化,得到状态方程和测量方程。
①状态方程:

[u(k)+w(k)]
(13)
②测量方程:
yv(k)=[02.5]x(k)+v(k)
(14)
4.1参数设置
①SOA算法参数设置。
搜寻种群规模为30,个体维数为3,每一维待优化参数kp、ki和kd的初始取值在[0,100]内随机选取,且在优化过程中,取值范围均限定为[0,100]。最大进化代数为100,目标函数中参数β1=0.999、β2=0.001、β3=100。参数搜索的步长由高斯隶属度函数确定[12],隶属度最大值和最小值分别设定为0.985和0.011,预动方向的惯性权值随着进化代数由0.9线性减小到0.1,利己方向和利他方向的权值均设定为0.5。
②卡尔曼滤波器参数设置。

4.2结果比较与分析
设系统输入为单位阶跃信号r=1,取一组经验参数值kP=15、ki=120、kd=0.8,则加入与未加入卡尔曼滤波器的常规PID控制阶跃响应比较如图3所示。
经过SOA算法优化后的PID控制参数为kp=22.873 1、ki=82.186 5、kd=1.598 7。基于SOA-卡尔曼和基于卡尔曼的PID参数单位阶跃响应比较如图4所示。

图3 常规PID控制阶跃响应比较图
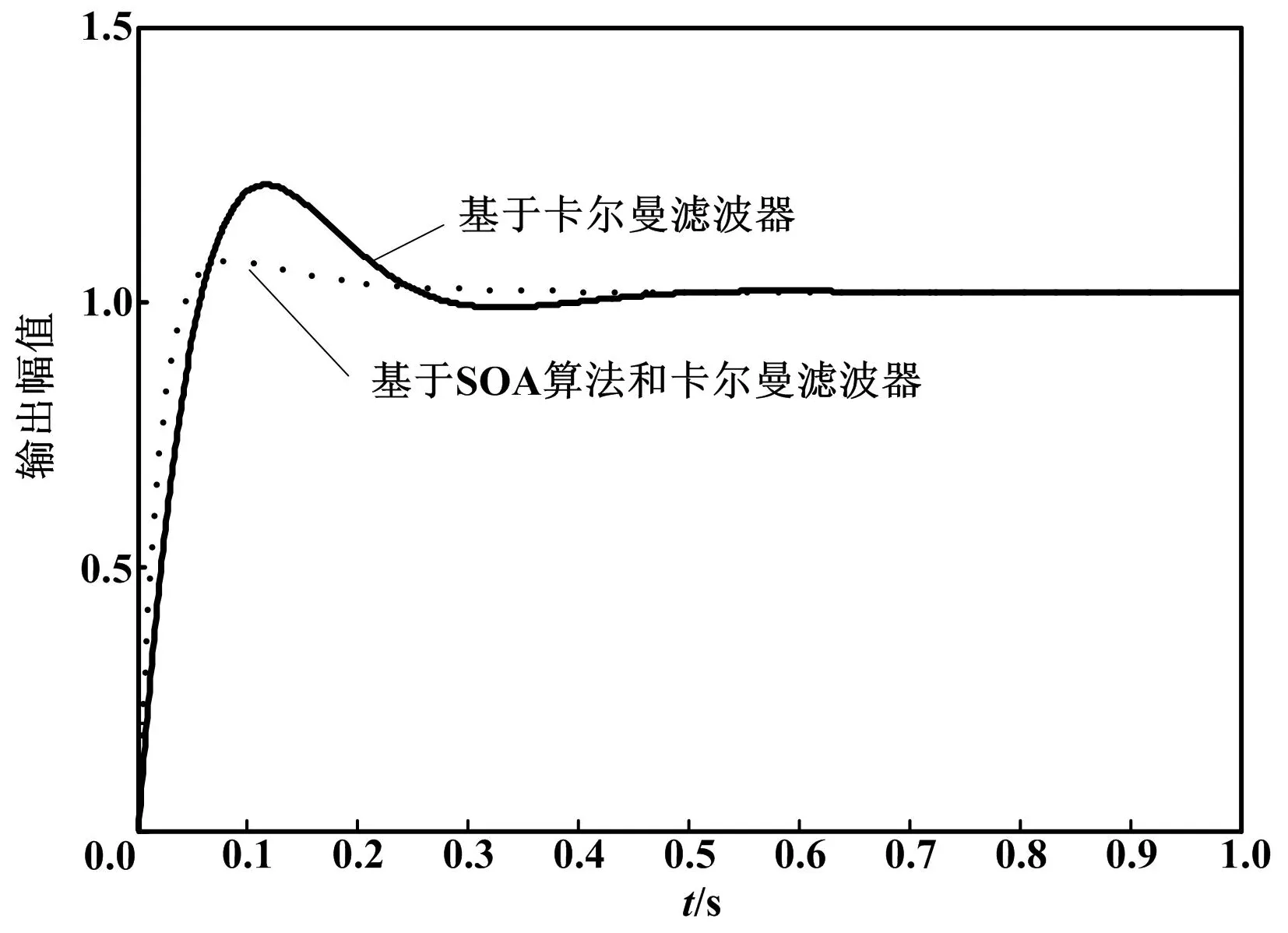
图4 PID参数单位阶跃响应比较图
根据SOA算法优化后的PID参数值,并结合PID参数在校正环节中的作用,得到更佳的PID控制参数kp=23、kI=60、kd=2.2。校正后的SOA优化参数阶跃响应曲线如图5所示。

图5 校正后SOA优化参数阶跃响应曲线
结果分析如下:
①由图3可知,加入卡尔曼滤波器的PID控制系统超调量减小、震荡次数减少,并能迅速达到稳定态,有效降低了白噪声的影响。
②由图4可知,结合SOA算法和卡尔曼滤波器的PID控制系统不仅可以抑制对系统性能有较大影响的控制噪声和测量噪声,而且系统上升时间和稳态时间加快,超调量和震荡次数明显减少,系统的动态性能和静态性能均得到了提高。
③由图4和图5可知,SOA算法不易直接优化得到最佳的PID参数,但优化后的PID参数值为PID系统参数的最佳整定提供了非常有效的参考依据。
5 结束语
针对PID控制系统的控制参数调整困难,以及在控制过程中噪声对系统性能的影响,提出了基于搜寻者优化算法和卡尔曼滤波器相结合的PID控制方法。结果表明,该控制方法可以得到较优的PID参数,并能有效抑制控制干扰信号和测量噪声信号,使系统具有更快的调节速度和更好的稳定性,控制性能有较大的改善。
[1] 张世峰,李鹏.基于神经网络的自整定PID控制器设计[J].自动化仪表,2009,30(7):64-66.
[2] 王晓娜,左晓菲,张辉,等.Smith模糊PID匀速升温控制策略研究[J].自动化仪表,2015,36(1):87-90.
[3] 蔡超,周武能.人工蜂群算法整定PID控制器参数[J].自动化仪表,2015,36(8):74-77.
[4] 谢攀,谭功全,张昌华.一种简单的低阶时滞过程PID参数优化方法[J].自动化仪表,2013,34(6):12-19.
[5] 刘晴,张正刚,丁维明.神经网络预测PID控制在气化炉中的应用[J].自动化仪表,2014,35(5):60-62.
[6] 邓丽,蒋婧,费敏锐.基于免疫粒子群算法的PID参数整定与自适应[J].自动化仪表,2013,34(2):65-67.
[7] 孙莉,赵志光.模糊PID控制器在水泥回转窑的应用[J].自动化仪表,2014,35(1):26-29.
[8] DAS S,PAN I,HALDER K,et al.LQR based improved discrete PID controller design via optimum selection of weighting matrices using fractional order integral performance index[J].Applied Mathematical Modelling,2013,37(6):4253-4268.
[9] SIMON D.Kalman filtering with state constraints: a survey of linear and nonlinear algorithms[J].Control Theory & Applications,IET,2010,4(8): 1303-1318.
[10]鄢华林,齐圣民.卡尔曼滤波抗积分饱和PDF控制系统研究[J].自动化仪表,2015,36(2):5-7.
[11]DAI C H,ZHU Y F,CHEN W.Seeker optimization algorithm[C]//International Conference on Computational Intelligence and Security.IEEE,2006:167-176.
[12]戴朝华.搜寻者优化算法及其应用研究[D].成都:西南交通大学,2009.
PID Control Combining Seeker Optimization Algorithm and Kalman Filter
Parameter tuning of traditional PID controller depends on experience,and in control process,the system is easily affected by a variety of noises,in order to settle these problems,the PID control method based on combination of seeker optimization algorithm and Kalman filter is proposed.The seeker optimization algorithm is used to optimize PID parameters intelligently,and Kalman filter is used to effectively suppress the control noise and measurement noise.A second order system with delay is simulated,and the results show that compared with the traditional PID control method,this method can achieve intelligent PID control to get better PID parameters and effectively eliminate noise interference in the process of control,to implement intelligent PID control which is featured with good performance in quick regulation speed,low steady-state error and strong anti-interference capability.
Kalman filterControl systemIntelligence algorithmSeeker optimization algorithmPID controlParameter tuningNoiseInterference signal
TH-39;TP273+.2
A
10.16086/j.cnki.issn 1000-0380.201609005
修改稿收到日期:2016-01-05。
作者刘俊(1986—),男,2013年毕业于太原科技大学控制工程专业,获硕士学位,讲师;主要从事人工神经网络、优化算法和智能控制方向的研究。
