全冷式超大型液化气船波浪载荷预报与分析

2016-10-12周清华梁小军李小灵

中国航海 2016年3期

关键词：船体波浪弯矩

周清华, 梁小军, 李小灵, 陈兵

(江南造船(集团)有限责任公司，上海 201913)

全冷式超大型液化气船波浪载荷预报与分析

周清华, 梁小军, 李小灵, 陈兵

(江南造船(集团)有限责任公司，上海 201913)

全冷式超大型液化气船(Very Large Gas Carrier,VLGC)的运动及波浪载荷预报对船体、围护系统和液舱支座的结构安全性评估至关重要。对此,以83 000 m3VLGC为例，采用WALCS程序系统作为主要分析工具，应用三维线性势流理论，在频域内预报该VLGC船体运动与波浪载荷的传递函数和长期预报极值。以第二液货舱重心处的加速度和舯剖面的垂向波浪弯矩为研究对象，比较分析WALCS预报值与IGC设计值、UR-S11规范值及SESAM预报值的差异。分析结果可为VLGC的结构安全性评估提供载荷输入和参考。

全冷式超大型液化气船(VLGC)；加速度；垂向波浪弯矩；传递函数；长期预报

Abstract: Ship motion and wave load prediction of Very Large Gas Carrier(VLGC) is essential for the safety assessment of hull structure, containment system and tank support. An 83 000 m3VLGC is taken as the object of study for illustration. The hydrodynamic analysis software WALCS based on three dimensional linear potential flow theory is used as the primary analytical tool to predict the hydrodynamic characteristics of ship motion and wave load in frequency domain. The gravity acceleration of second cargo tank and the vertical wave bending moment of midship section are calculated. The WALCS forecast values are compared with those from IGC rule,UR-S11 standard and SESAM. The calculated results can be a reference of the excitation input for the structural safety assessment of VLGC.

Keywords: VLGC； acceleration； vertical wave bending moment； transfer function； long term prediction

83 000 m3全冷式超大型液化气船(Very Large Gas Carrier,VLGC)[1]是江南造船(集团)有限责任公司研制的高技术、高附加值船舶，打破了国外船厂的技术垄断。相比常规船型，VLGC对船体波浪载荷预报的要求更高，主要原因有：

(1) 船长超过200 m，质量分布特殊，规范计算法不足以反映其在恶劣海况下的载荷响应特征；

(2) 液货加速度产生内部液体压力，应考虑船体运动的长期预报;

(3) 围护系统的安全性要求高，该船设置有4个A型独立棱形液舱，并通过特殊的支座支撑在货舱内，承受液舱和货物的质量及各类静、动载荷，由于支座只承受压力而不传递拉力，因此在进行VLGC结构分析时需进行接触分析或大量迭代运算。[2]

由此可见，为保证船体、围护系统和液舱支座的结构安全性，准确计算出船体运动加速度和波浪载荷尤为重要。目前船舶在波浪中的运动和载荷响应预报方法[3]已日臻成熟，主要有切片理论、三维理论、非线性时域理论及考虑弹振的水弹性理论等。这些方法中，基于势流理论的三维频域线性计算方法[4]在工程中应用较为广泛。船级社和相关科研院校已开发出相应的软件，如DNV/SESAM,BV/HYDROSTAR和MIT/WAMIT等。这里选取WALCS程序系统对83 000 m3VLGC的运动及波浪载荷进行预报与分析。该船的技术参数为：总长226 m；垂线间长215 m；型宽36.6 m；型深22.2 m；设计吃水11.4 m；载重量54 000 t；设计航速16.8 kn。为验证WALCS数值计算的有效性，以加速度和垂向波浪弯矩为研究对象，比较分析WALCS预报值与IGC设计值、UR-S11规范值及SESAM预报值的差异。

1 WALCS波浪载荷计算原理

WALCS 软件可用来计算低速航行于有限和无限水深规则波中的船舶或海洋平台的运动、脉动压力及剖面载荷的稳态响应。

基于线性势流理论，流场总速度势φ(x,y,z,t)[5]可表示为

(1)

式(1)中:φT(x,y,z)=φI(x,y,z)+φD(x,y,z)+φR(x,y,z)；φS为定常兴波势；U为航速；ω为遭遇频率；φT为非定常速度势；φI为入射势,已知；φD和φR分别为绕射势及辐射势,均为非定常扰动势。

频域内低航速船舶运动非定常扰动势需满足以下定解条件。

1) 域内条件[L]

(2)

2) 线性自由面条件[F]

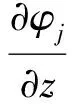
(3)

3) 物面条件[S]

(4)

4) 底部条件[B]

(5)

5) 远方辐射条件[R]：相应的远方辐射条件。

式(2)～式(5)中：φj(j=1,2,…,6)为单位复速度的j模式运动辐射势；φ7为单位波幅的绕射势；v=ω2/g；n为船舶表面指向内部的单位法线向量。

根据刚体动力学原理导出规则波中船舶运动微分方程为

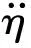
[K]{η(t)}={f(t)}

(6)

式(6)中:[M]为船舶质量矩阵；[Ma]为附加质量矩阵；[C]为阻尼矩阵；[K]为静恢复力矩阵；{η(t)}为六自由度刚体运动；{f(t)}为波浪干扰力。

采用高斯消去法对式(6)进行求解，得到船舶运动响应的稳态解。利用线性化的伯努利方程，并计入静水压力变化部分的贡献，得到作用于船体湿表面上总的脉动压力为

P(x,y,z,t)=Re{P(x,y,z)eiωt}

(7)

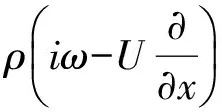
求解船体运动响应和脉动压力之后，应用达朗贝尔原理计算船体剖面内的波浪诱导力和力矩。

2 实船计算

2.1计算模型

WALCS采用基于自由面格林函数的三维频域方法,通过在船体湿表面分布奇点来求解流场速度势，要求创建水动力面元模型。模型网格的划分以四边形单元为主，其大小取为4倍的纵骨间距，网格总计1 968个。定义船壳网格为湿表面，指定波浪水动压力的矢量法向为由流体指向船壳表面。图1为VLGC水动力面元模型。

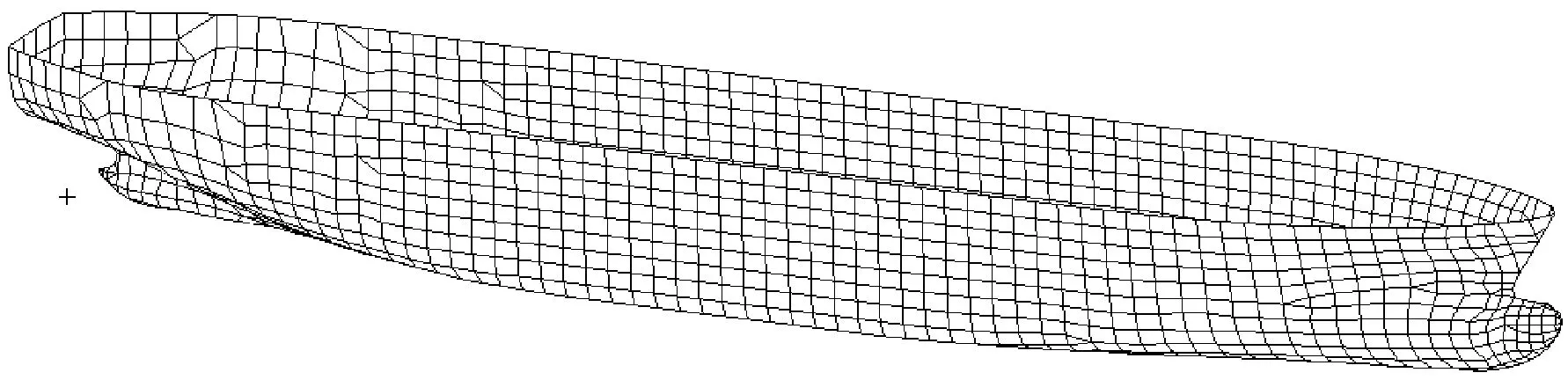
图1 VLGC水动力面元模型

计算波浪载荷时需提供准确的质量模型。为计算剖面载荷，采用WALCS提供的分段质量模型方式创建整船质量模型。

2.2传递函数

为充分观察不同浪向角的波浪对船体运动和波浪载荷的影响规律，共选取13个浪向角(0°～180°，间隔15°，各浪向的概率分布认为是均匀的)、29个波浪频率(0.10～1.50 rad/s，步长取0.05),水深为无限水深;采用临界阻尼法对横摇阻尼进行修正，临界阻尼系数取0.05；沿船长从艉垂线至艏垂线选取21个剖面作为计算剖面。选取液舱装载率为100%时的典型工况作为计算工况，不存在液舱晃荡问题。

船体运动和主要载荷控制参数的传递函数(RAO)见图2～图4。

图2中:不同浪向下的垂荡和横摇幅频响应曲线吻合程度均较低，表明浪向对船体运动响应的影响较大；横浪时，垂荡和横摇响应达到最大。图3中，垂向波浪弯矩幅频响应曲线为单峰曲线，峰值出现在舯剖面附近。图4中，垂向波浪剪力幅频响应曲线为双峰曲线，峰值出现在距艉垂线1/4船长和3/4船长的剖面附近。载荷峰值均出现在浪向角为0°，频率为0.50～0.55 rad/s时，即船舶在迎浪航行、遭遇波长/船长为0.95～1.15的波浪时，垂向波浪弯矩和垂向波浪剪力响应最大。可见，WALCS预报值与实际规律一致。

a) 垂荡

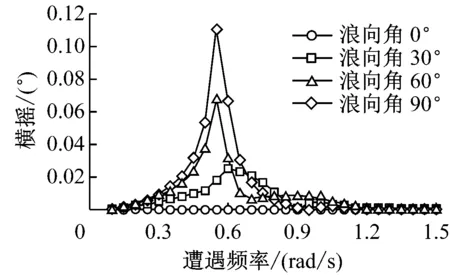
b) 横摇

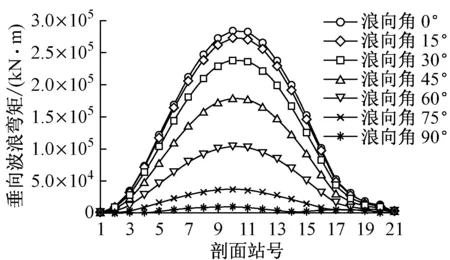
a) 不同浪向(遭遇频率为0.5 rad/s)

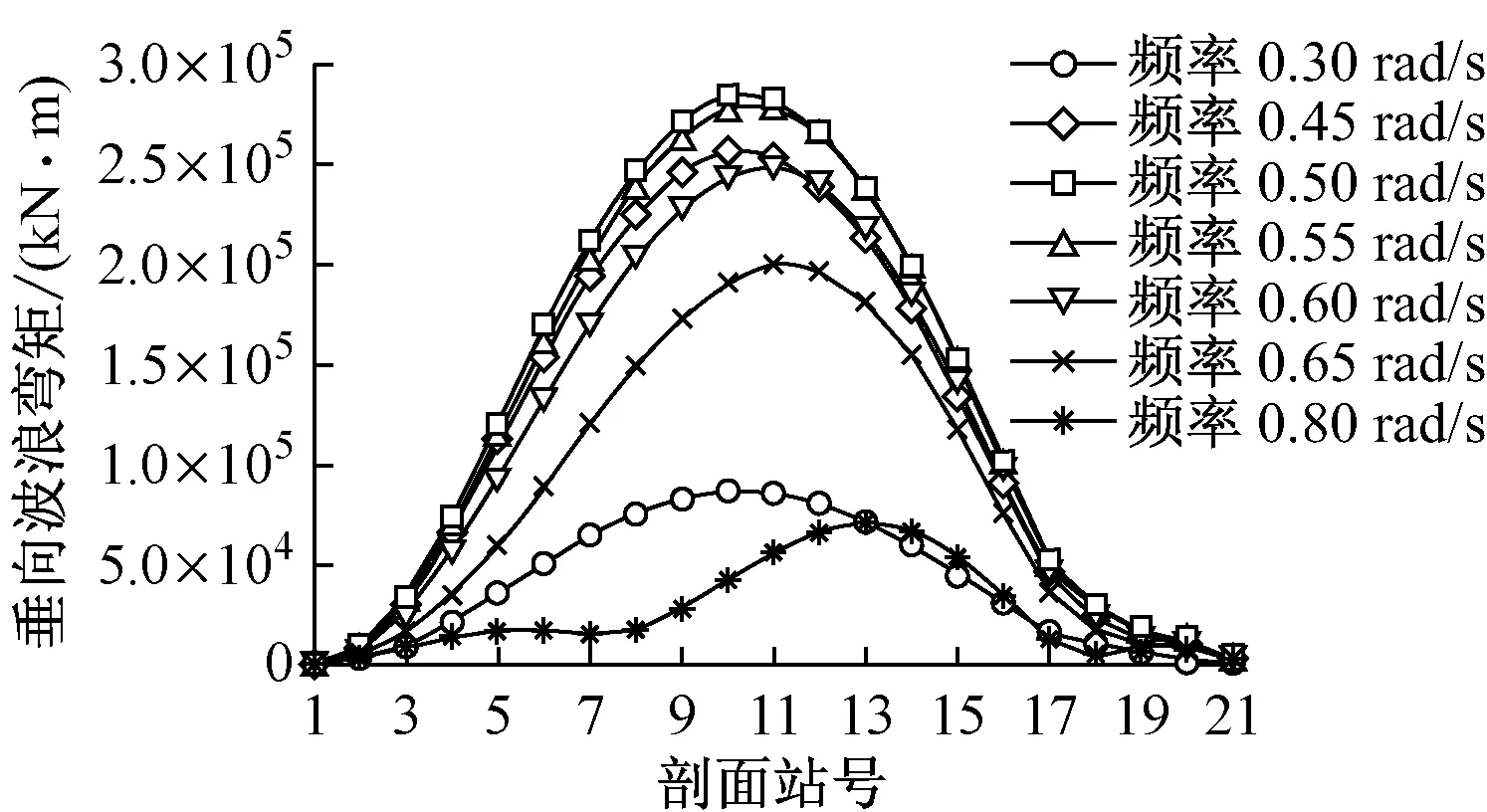
b) 不同频率(迎浪)

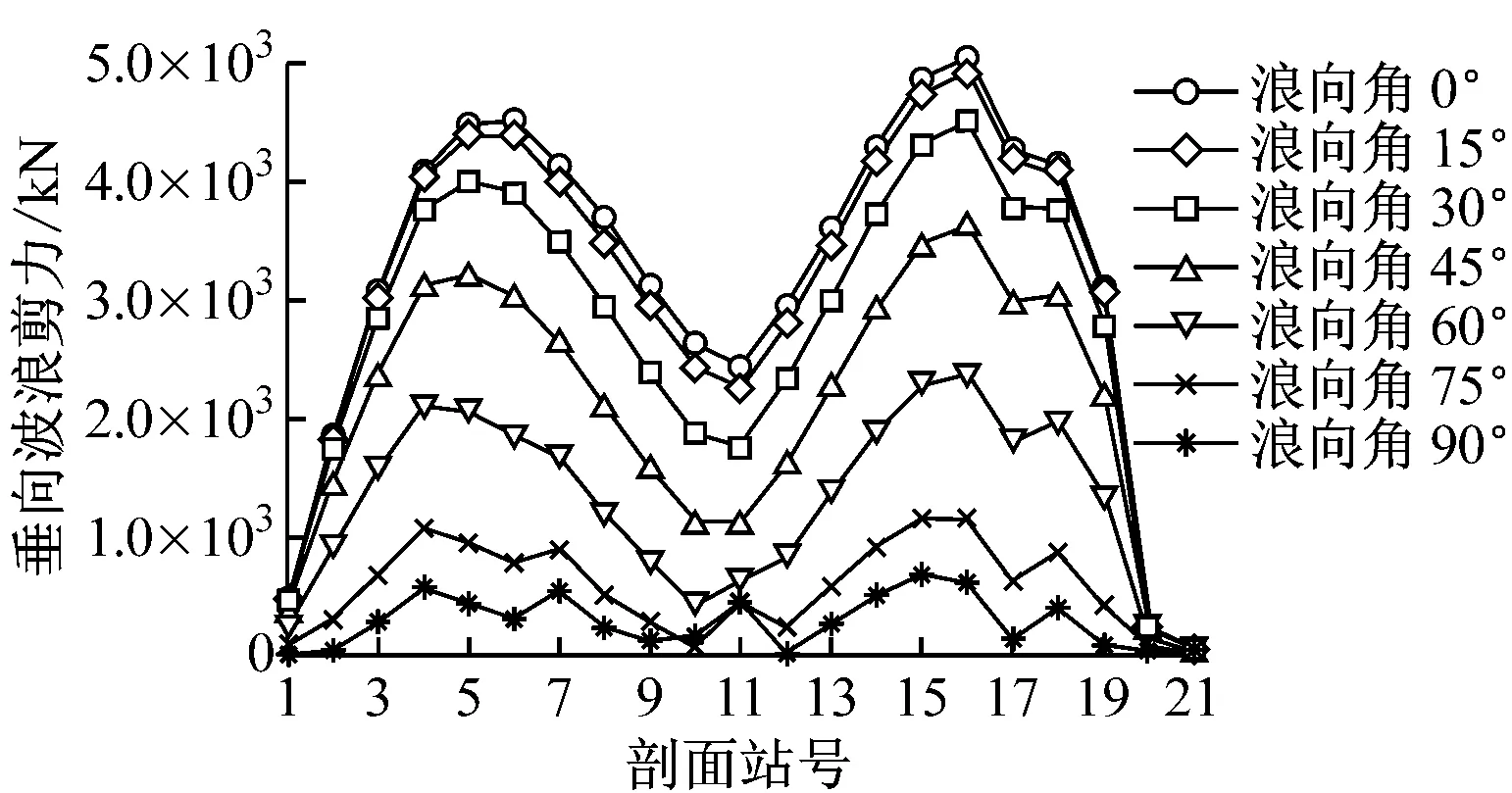
a) 不同浪向

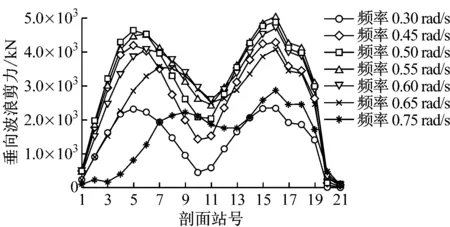
b) 不同频率

2.3长期预报

长期预报中，选取北大西洋波浪散布图作为海浪统计资料，采用ISSC双参数谱模拟散布图中的海况，运用威布尔分布拟合长期分布，分别考虑长峰波和短峰波2种波浪形式;短峰波的扩散函数采用f(x)=2cos2θ/π，其中θ为波系相对于主浪向的夹角。

对第二液舱重心处的垂向加速度和舯剖面的垂向波浪弯矩进行长期预报，计算结果见图5。

图5中，在北大西洋海况下，垂向加速度和垂向波浪弯矩的长期预报极值与超越概率的对数的负值呈正比关系。

3 结果比较与分析

3.1加速度

a) 垂向加速度(组合浪向)

b) 垂向波浪弯矩(组合浪向)

《国际散装运输液化气体船舶构造和设备规则》(IGC规则)给出加速度分量的指导公式是船舶在北大西洋中以概率水平为10-8运动而产生的加速度，适用于船长>50 m的船舶。[6]指导公式为

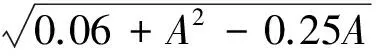
(8)

(9)

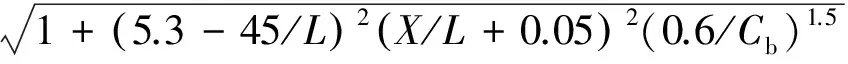
(10)

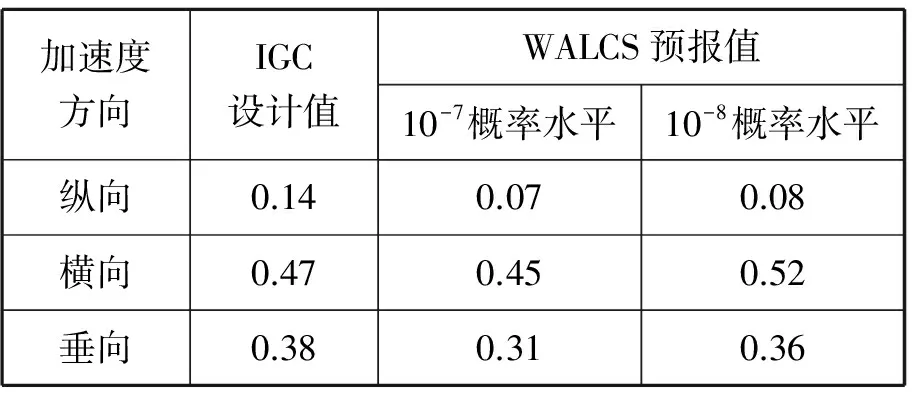
表1 加速度的IGC设计值和WALCS预报值 g

由表1可知：对比3个方向的加速度计算结果，纵向最小，垂向其次，横向最大;WALCS的纵向加速度预报值远小于IGC设计值，最大偏差为50.0%；横向加速度的IGC设计值位于WALCS在10-7～10-8概率水平下的预报值区间内；WALCS在 10-8概率水平下的垂向加速度预报值略低于IGC设计值，偏差为5.2%。经分析，IGC指导公式中的加速度与航速呈正比，选取设计航速计算，而WALCS选取零航速计算，两者的差异对纵向加速度计算的影响较大。基于线性频域方法的WALCS在高航速下的纵向加速度预报精度还有待通过波浪载荷模型试验进一步验证，横向加速度和垂向加速度的计算结果在可接受的范围内。

3.2垂向波浪弯矩

国际船级社协会(International Association of Classification Societies,IACS)于1991年提出UR-S11，即对常规船舶的总纵强度提出统一要求。[7]该要求规定舯部垂向波浪弯矩设计值按以下公式求出。

中垂Ms=0.11CL2B(Cb+0.7)

(11)

中拱Mh=0.19CL2BCb

(12)

式(11)和式(12)中:L,B和Cb分别为船长、船宽及方形系数;系数C由式(13)确定。

(13)

由式(13)可知，IACS设计值仅与L,B和Cb有关，未计入船体线型、质量分布和航行条件等对船体载荷有重要影响的因素，相当于大量船舶的统计平均值。[8]

表2为垂向波浪弯矩的规范计算值和直接预报值;图6为WADAM计算的10-8概率水平下舯部垂向波浪弯矩的长期预报极值曲线；图7为WASIM计算的规则波激励下舯部垂向合成弯矩时历曲线。

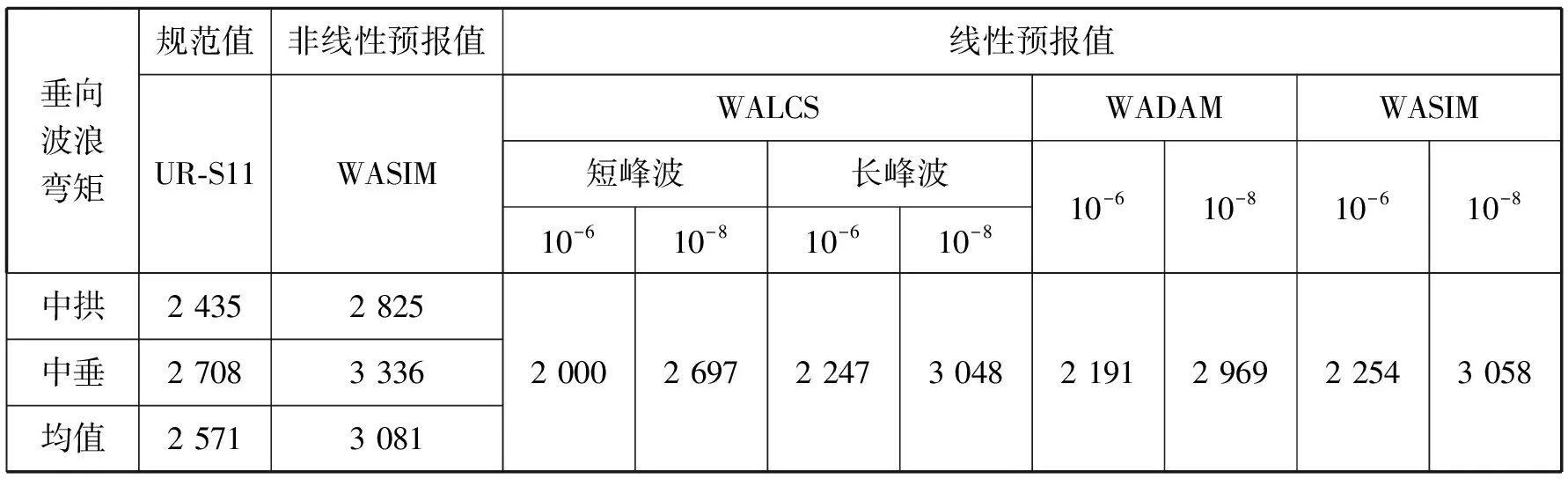
表2 垂向波浪弯矩的规范计算值和长期预报值 MN·m

图6 10-8概率水平下舯部垂向波浪弯矩长期预报极值曲线

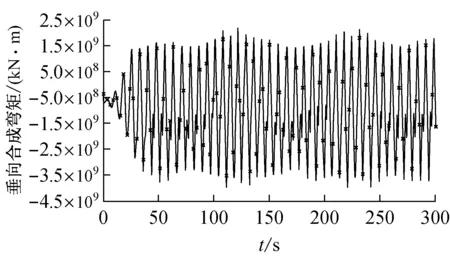
图7 规则波激励下的舯部垂向合成弯矩时历曲线

由表2可知：采用线性方法预报，3种计算程序的长峰波预报值比较吻合，偏差不超过3%；与长峰波相比，弯矩的短峰波预报值在10-6概率水平和10-8概率水平下均要小约11%，该结论与文献[8]中的计算结果一致；UR-S11规范值均位于线性程序在零航速10-6～10-8概率水平下的长峰波预报值区间内，UR-S11规范计算的均值与10-8概率水平下的短峰波预报值更为接近；考虑自由液面、瞬时效应和航速等非线性因素之后，中垂状态下的垂向波浪弯矩值大于中拱状态下的垂向波浪弯矩值；WASIM非线性预报值最大，其均值与10-8概率水平下的长峰波预报值较为接近。