基于模糊推理系统的船舶操纵运动建模

白一鸣, 赵永生

(大连海事大学 信息科学技术学院， 辽宁 大连 116026)

基于模糊推理系统的船舶操纵运动建模

白一鸣, 赵永生

(大连海事大学 信息科学技术学院， 辽宁 大连 116026)

基于典型的船舶操纵运动试验(Z型试验)的实船数据，通过运用数据挖掘技术提取模糊规则，架构模糊推理系统,对船舶操纵运动系统进行建模和预报。为提高预测精度，利用调整模糊集区间划分的方法优化模糊推理系统，使模糊推理系统的结构与样本数据分布相适应。实船操纵运动时间序列数据预报的仿真结果证实了所提出的基于数据挖掘技术的模糊推理系统的实用性和有效性。支持度与信任度2个数据挖掘概念的引入能帮助模糊推理系统从实际采集数据中提取模糊规则，对实现复杂系统的智能建模与控制具有重要意义。

水路运输； 船舶操纵；模糊建模；数据挖掘

Abstract: In order to model the ship motion, a set of typical ship maneuvering motion data is collected from ship zig-zag tests. The ship maneuvering motion is modeled and forecast by the fuzzy inference system constructed with data mining technology. To improve the accuracy, the fuzzy inference system is optimized with a partition refining strategy, which can adapt the fuzzy inference system to the data set. The simulation of actual time serial data in ship maneuvering motion proves that the fuzzy inference system based on the data mining technology is a useful and effective method. The concepts from the data mining, the support degree and the confidence degree are introduced, which is essential in extracting fuzzy rules from numerical data for fuzzy modeling and control.

Keywords: waterway transportation; ship maneuvering； fuzzy modeling； data mining

船舶操纵性能反映船舶航行过程中的水动力性能，与船舶航行的安全性和经济性密切相关。近年来，随着航运业迅速发展，船舶日益大型化、快速化，油船、集装箱船、化学品船及液化气船等特种船增多，加上海域油气田开发和沿海养殖面积扩大，使得海上交通密度变大、航运环境恶化、航行干扰因素增多及船舶操纵难度加大。对此，国际海事组织(International Maritime Organization, IMO)于1985年提出估算船舶操纵性能的初步指南，规定船舶操纵性的基本要求;之后又于1993年和2002年分别颁布船舶操纵性暂行标准及船舶操纵性标准，对操纵性预报和船舶应满足的操纵性指标明确地提出定量要求，极大地促进了船舶操纵运动的研究。[1-2]

目前，对船舶操纵运动的建模主要有经验公式(数据库)法、约束模型试验法、理论与数值计算方法及结合模型试验的系统辨识法等4种方法。

1) 经验公式(数据库)法受船型制约，对超出数据库范围的船型很难达到预报精度。

2) 约束模型试验法强迫船模在约束条件下作精确控制运动。但是,由于存在“尺度效应”，其影响难以分析,因此需进行系列船模试验。这样，不仅需要特殊的试验设施，而且十分费时、费力。

3) 理论与数值计算法通过采用各种数值方法求解流体运动的控制方程，计算相应的船舶水动力导数。但是,要计算所有的水动力导数，特别是非线性水动力导数，目前还有很大困难。

4) 结合模型(实船)试验的系统辨识法把船舶看作是一个非线性动态系统，进行自由自航模型试验,并由测量得到的系统输入和输出数据，通过系统辨识得到船舶操纵运动模型。该方法适于研究船舶航行过程中的风、浪、流等环境因素对船舶操纵性的影响。特别是随着试验测量技术和系统辨识方法的不断发展，基于系统辨识的船舶操纵运动建模方法拥有广阔的应用前景。[3-10]

这里利用实船数据建立船舶操纵运动模型来反映船舶对操舵的转艏运动响应。该方法通过对船舶操纵运动的输入、输出数据进行采样并作一定的处理和计算建立描述船舶操纵运动过程的输入-输出特性模型，对操纵运动动力学特性的细节描述不作要求。该建模方法借鉴经典控制理论，是一种基于数据驱动理念的黑箱建模方法。[11]为建立船舶操纵运动的模糊推理模型，在提取模糊规则算法的过程中引入数据挖掘中的支持度和信任度的概念改进模糊规则提取算法，使模型对船舶航行过程中的风、浪、流等噪声干扰有更好的鲁棒性。[12]在针对实船Z型试验数据建立船舶操纵时间序列模型的过程中，相比传统的建模方法，该模糊模型无需依据固有的框架确定船舶操纵模型中的各项动态系数，避免了生成不匹配模型的情况，因此能进行较精确的系统辨识和数据预报。

1 获取船舶Z形操纵运动试验数据

利用数据挖掘建模方法对船舶操纵Z型试验数据建立预测模型，并验证该方法的有效性和实用性。Z形操纵试验[13]是一种评价艏摇抑制性的试验。时间序列采样数据为大连海事大学“育鲲”号实习船(见图1)20°/20° Z型试验的实船数据。试验中，船舶的直线定常航速设定为15.5 kn，初始航向为140°。开始进行Z型试验操纵后，每间隔2～8 s由2名记录人员分别记录一次船舶实时航向数据。表1为实船20°/20° Z型试验采样数据示例。这里采用210条不同时间点的采样数据，每条采样数据均给出采样时间及其对应的船舶航向和航向偏差(实际航向与初始航向的差值)。图2为记录的2组航向和航向偏差曲线及由此得到的平均航向偏差的时间序列曲线。由于实船试验受到复杂海况的影响，存在噪声和异常数据,因此实船航向偏差曲线并不是光滑曲线。

获得船舶操纵时间序列数据点之后，为运用数据挖掘算法建立船舶操纵时间序列预报模型，首先需将时间序列中的数据点变换成输入-输出的数据对形式,具体的转换方法如下。

图1 大连海事大学“育鲲”号实习船

表1 实船20°/20°Z型试验采样数据示例

设x(t+k×Δ)(k=1,2,3，…)是一个标准的时间序列,t为初始时刻，Δ为时间间隔。假设已知该时间序列的M个数据点。这些数据点通过式(1)很容易转换成输入-输出数据对形式。

{x(t+(M-m)Δ),…,x(t+(M-1)Δ);

x(t+MΔ)}

{x(t+(M-m-1)Δ),…,x(t+(M-2)Δ);

x(t+(M-1)Δ)}

⋮

{x(t),…,x(t+mΔ);x(t+(m+1)Δ)}

(1)

这样，时间序列预测问题就转换为寻找输入-输出数据间的非线性映射关系Fm的问题。

x(k-(m-2)Δ),…,x(k-Δ),x(k)}

(2)

2 船舶操纵运动系统的模糊建模

模糊推理系统模型是进行船舶操纵预报的基础,而模糊系统建模成功的关键是保证模糊规则的质量。这里基于数据挖掘技术建立模糊推理系统模型,主要思路是运用数据挖掘中的支持度与信任度的概念进行模糊规则的提取和优化。一般给定式(3)形式的样本数据对。

(3)

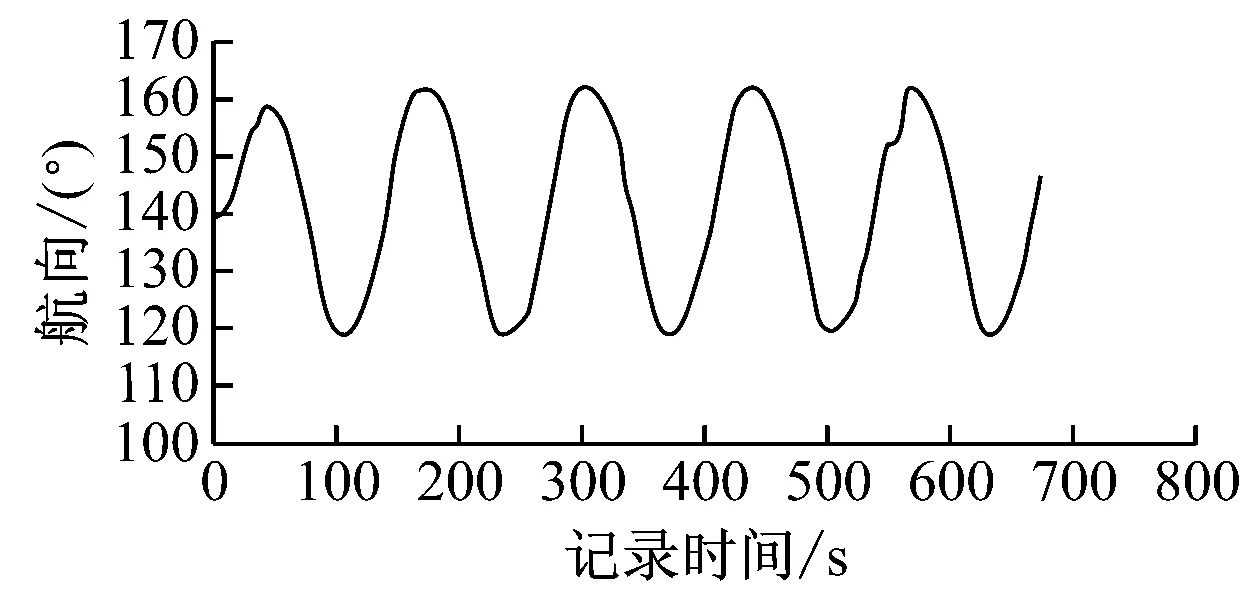
a) 记录1的航向曲线

b) 记录2的航向曲线

c) 记录1各时间点的航向偏差曲线

d) 记录2各时间点的航向偏差曲线

e) 平均航向偏差的时间序列曲线

依据式(1)，设定m=4,将时间序列数据转换成四输入、单输出的数据对形式，即式(1)中n=4；同时，将航向角偏差输入、输出数据对分为2组，前100对输入-输出数据作为训练数据，剩余的数据对作为测试数据。

2.1划分输入和输出变量区间为模糊区间(步骤1)

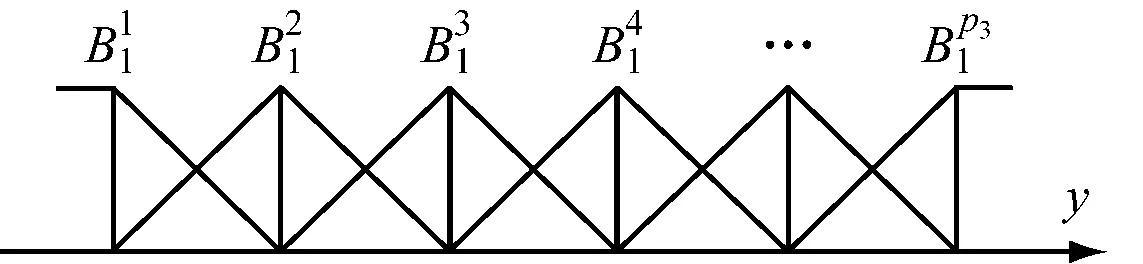
图3 输入-输出区间的模糊集划分及其对应的隶属度函数

这里采集的实船试验记录航向偏差的最大值为22.1°，最小值为-21°。因此，将模糊建模中输入-输出变量x1，x2，x3，x4及y的变化范围都设定为[-21°,22.1°]。

2.2普通记录转化成模糊记录(步骤2)

步骤1划分的每个模糊集都需分配相应的隶属度函数。这里采用三角形隶属度函数定义模糊集划分，其表达式为

(4)

式(4)中:xc为模糊隶属度函数值达到最大值1时所对应的输入变量的取值;σ1和σ2由步骤1设定。

人力资源开发是一个计划性、系统性的工作，事业单位完成岗位设置后，还需做好岗位评价工作，建立岗位退出工作，较好解决人员的出口问题。基于此，必须修订、完善事业单位绩效考核工作，明确优秀人员奖励、不合格人员惩处措施以及未聘人员分流、社会保险制度衔接等问题，切实保证人力资源开发获得实效。

在实际系统模型中，各个模糊集都有其实际的物理意义。这里利用模糊集及其对应的隶属度函数值的形式表示航向偏差的输入-输出数据对，即将普通记录

(5)

转化为模糊记录

p=1,2,…,N

(6)

2.3定义模糊规则的支持度(步骤3)

从数据挖掘的角度来看，若一条模糊规则有实际意义，则其必须具有足够的支持度。支持度反映输入-输出样本数据对该条规则的支持程度，这里将规则的模糊支持度定义为

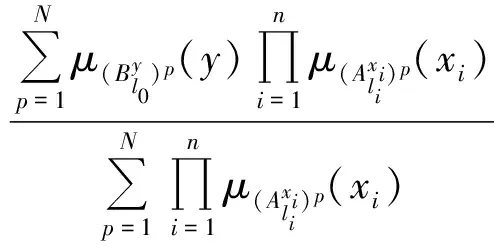
(7)

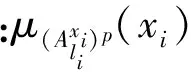
为强调和明确该遍历算法的基本原理，给出该遍历算法的程序流程(见图4)。当所有数据点依次进入各个输入子区间划分之后，模糊规则的IF条件部分也随之确定。为确定规则的THEN结论部分，需依次计算各输出模糊集所对应的支持度supB1(Ri),supB2(Ri),…,supBp3(Ri)，并选用最大支持度规则作为该输入模糊区间划分的模糊规则。即

(8)

图4 遍历算法程序流程

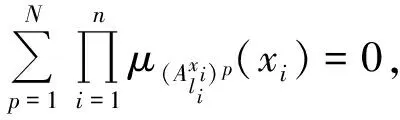
2.5计算模糊规则的信任度约减规则数目(步骤5)

模糊系统的核心是一个从输入区间映射到输出区间的模糊规则集合。上述4个步骤组成的模糊规则挖掘算法生成一个完备的模糊集。但随着输入变量的个数和模糊集划分增多，模糊规则的数目也呈指数增长。因此，需通过引入信任度的概念来约简规则，提高系统的执行速度。信任度的计算式如下。

首先，计算各条规则输出误差的加权平均值,即

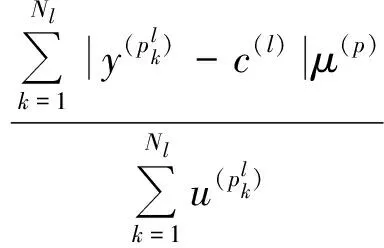
(9)

式(9)中:Nl为权重不为0的数据点个数;c(l)为规则结论模糊集的中心值。根据规则误差的加权平均值，定义各条规则的信任度为

(10)

通过上述5个步骤即可完成模糊规则的提取和精简。在提取模糊规则之后, 采用单值模糊化、乘积运算和加权平均反模糊化即可得到以下解模糊模型。

(11)

3 船舶操纵运动系统的优化与仿真

通常基于实际数据设计模糊推理系统包含系统辨识和系统优化2部分，这里采用调整输入区间模糊集划分的方法进行系统优化，主要包含以下3步。

1) 以简单的模糊区间划分初始化模糊系统。

2) 依据数据分布调整模糊集区间划分参数。

3) 在误差最大的模糊划分区间增加模糊集区间划分。

这3步循环迭代执行，以生成不同精度、不同复杂度的模糊推理系统架构。为保证航向偏差预测值与真实值的误差<3°，船舶航向偏差输入区间最终被划分为10个不等分的模糊集区间(见图5)。详细的优化区间划分方法见文献[14]和文献[15]。

图5 调整后的模糊集划分

运用数据挖掘算法提取模糊规则架构模糊推理系统。实际航向、预测航向及误差的时间序列曲线见图6，可看出:船舶航向偏差变化的预测误差范围为[-2.5°，+2.5°]，满足预先设定的<3°的目标;航向偏差预测曲线更加光滑，能充分体现船舶操纵运动性能。因此，仿真结果验证了所提出的基于数据挖掘技术的模糊推理系统进行船舶操纵运动预测的有效性。

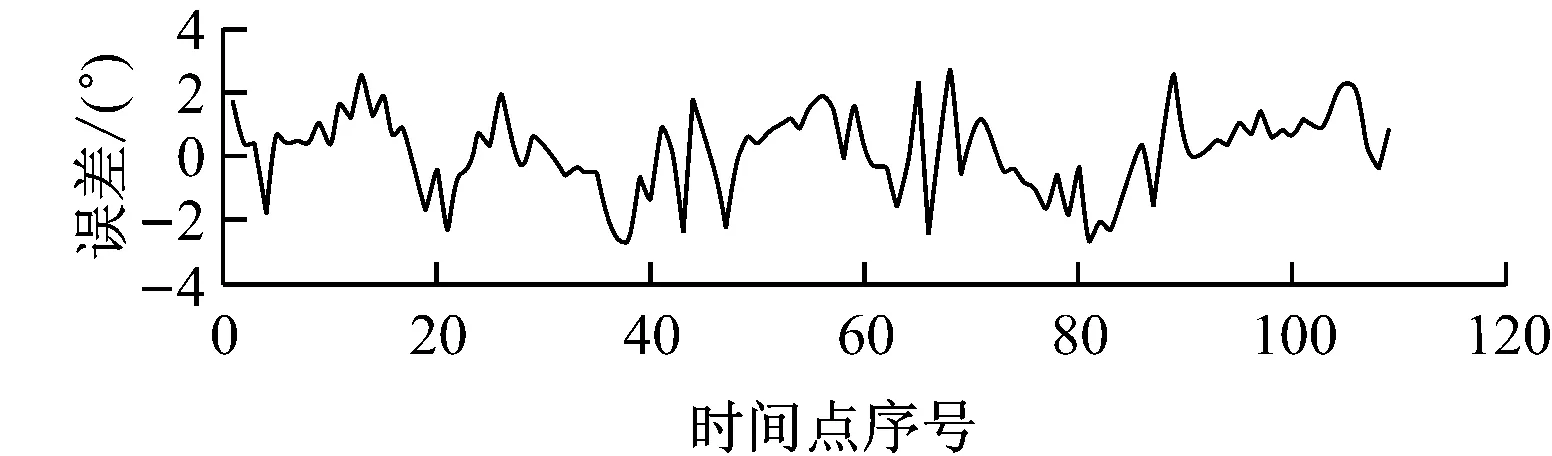
图6 实际航向、预测航向及误差的时间序列曲线

4 结束语

针对船舶操纵运动预报这一实际问题，提出一种基于数据挖掘算法的模糊推理系统架构方法,并依据实船数据对船舶操纵运动时间序列进行预测。该模型的预测结果证实所提出的数据挖掘方法具有一定的实用性和有效性。

[1] IMO Interim Standards for Ship Maneuverability: A.751(18)[S]. 1993.

[2] IMO. Standards for Ship Maneuverability: MSC. 137(76)[S]. 2002.

[3] ABKOWITZ M A. Measurement of Hydrodynamic Characteristic from Ship Maneuvering Trials by System Identi-fication[J]. Transactions of Society of Naval Architects and Marine Engineers, 1980, 88:283-318.

[4] KOSE K. On a New Mathematical Model of Maneuvering Motions of a Ship and Its Applications[J]. International Shipbuilding Progress, 1982,29(336):205-220.

[5] ITTC. Report of Maneuvering Committee[C]//Proc. of 24th ITTC, Edinburgh, UK, 2005: 138-146.

[6] VIVIANI M. A Method for the Identification of Hydrodynamic Coefficients from Standard Maneuvers[C]. Proc. of MARSIM 2003, Kanazawa, Japan, 2003.

[7] YOON H K, RHEE K P. Identification of Hydrodynamic Coefficients in Ship Maneuvering Equations of Motion by Estimation Before-Modeling Technique[J]. Ocean Engineering, 2003(30): 2379-2404.

[8] HADDARA M R, WANG Y. Parametric Identification of Maneuvering Models for Ships[J]. International Ship Building Progress, 1999, 46(445): 5-27.

[9] LEUNG S C, APPLETON B, SUN C. Fast Stereo Mat-ching by Iterated Dynamic Programming and Quadtree Subregioning[C]//Proceedings of the Conference on British Machine Vision. London: BMVA Press, 2004: 97-106.

[10] 罗伟林, 邹早建. 基于最小二乘支持向量机的船舶操纵运动建模[J]. 系统仿真学报, 2008, 20(13): 3381-3384.

[11] 张心光. 基于船舶操纵性试验分析的辨识建模研究[D]. 上海:上海交通大学, 2012.

[12] 王永富, 王殿辉, 柴天佑. 一个具有完备性和鲁棒性的模糊规则提取算法[J].自动化学报, 2010,36(9):1337-1342.

[13] 洪碧光. 船舶操纵. 大连海事大学[M]. 大连: 大连海事大学出版社, 2008：17-41.

[14] ROJAS I, POMARES H, ORTEGA J, et al. Self-Organized Fuzzy System Generation from Training Examples[J]. IEEE Trans. Fuzzy Syst., 2000, 8: 23-26.

[15] BAI Y M, ZHAO Y S. An Optimal Design Approach for Fuzzy Inference System from Data[C]. Proceedings of the 33rd Chinese Control Conference, Nanjing, 2014: 4526-4529.

ShipManeuveringMotionModelingBasedonFuzzyInferenceSystem

BAIYiming，ZHAOYongsheng

(Information Science and Technology College, Dalian Maritime University, Dalian 116026, China)

U661.33

A

2016-04-15

辽宁省博士科研启动基金(201501188)；大连海事大学教学改革项目(2016Y22)

白一鸣(1983—),男,辽宁海城人，实验师，博士，从事舰船避碰及模糊系统建模方向研究。E-mail:hs_bym@126.com

1000-4653(2016)03-0045-05