基于DSP的SSS定时同步算法的研究与实现

［石伟萍 沈钦仁］

基于DSP的SSS定时同步算法的研究与实现

［石伟萍 沈钦仁］

通过对现有小区搜索PSS定时同步算法的研究，结合Zadoff-Chu序列自身的特性，给出了一种基于SSS定时同步算法的实现方案，该算法复杂度低、易于实现，在存在频偏的情况下也能准确的计算定时同步点的位置。理论分析和仿真结果表明，该方案能够简化PSS定时同步的计算复杂度，可靠性高、易于实现。该方案已经在TMS320C64×DSP中实现，能够满足LTE-A系统小区搜索的性能要求。

LTE-A 辅同步信号 定时同步 DSP实现

石伟萍

商丘师范学院物理与电气信息学院助教，硕士研究生，研究方向：LTE物理层算法。

沈钦仁

重庆邮电大学通信与信息工程学院，硕士研究生，研究方向：多源光组播网络和网络编码。

1　引言

在LTE-A系统中，当用户终端（UE）开机后，首先需要搜寻周边小区，然后选择合适的小区注册。UE只有在注册到合适的小区后，才能后获取该小区及邻近小区更详细的信息，以便发起其他的物理层过程［1，2］。因此，小区搜索对于LTE（Long Term Evolution，长期演进）研究来说是一个重要方面。

小区搜索首先要进行定时同步，以往的定时同步主要利用PSS的对称性和良好的自相关性。通过研究发现SSS具有时域的共轭对称性，可以通过自相关来得到SSS地定时同步点，同时该算法能够抵抗频偏，在具有频偏时也能够准确的估计出定时同步点。通过理论分析和仿真结果表明，该算法复杂度低，可靠性好，易于实现，能够满足LTE-A系统性能需求。

2　理论分析及改进

2.1同步信号

LTE-A系统中，主同步信号采用频域Zadoff-Chu序列的方式进行生成，Zadoff-Chu具有良好的自相关特性。在LTE-A系统中有3组可用的主同步信号，通过根序列指示u进行区分。主同步信号的生成如下：

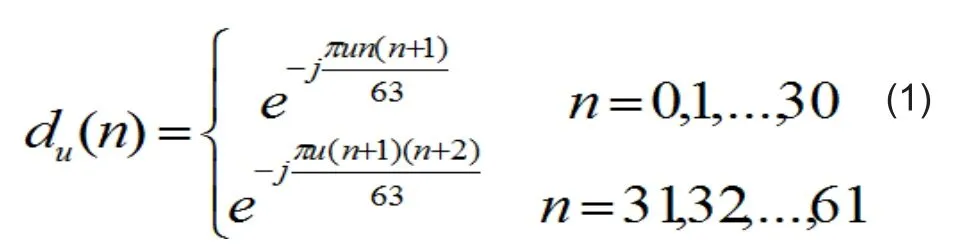
Zadoff-Chu序列的根序列指示u值如表1所示，它和一一对应。

表1　根序列指示u

辅同步信号序列d（0）,d（1）,...,d（61）由两个长度为31的二进制序列级联而成。级联后的序列通过主同步信号指定的扰码序列进行加扰。用于辅同步信号的两个长度为31的序列在子帧0和子帧5中是不同的，也就使得下行辅同步序列在这两个位置有了区别，公式如下：

主同步信号映射到LTE-A系统无线帧的子帧1和子帧6的第三个OFDM符号上，辅同步信号（SSS）在时隙1和时隙11的最后一个OFDM符号上发送。对于各种不同的系统带宽（5、10、15、20MHz），同步信号的传输带宽是相同的：占用频带中心的1.08MHz带宽。其中同步信号占用62个子载波，两边各预留5个子载波作为保护带。时频结构如图1所示，中间的DC被打孔，为直流载波。两边各有5个资源元素的保护间隔，该位置保留不发送任何信号。

图1　同步信号时频资源映射图

2.2算法分析及改进

频域主同步信号有3组，对应的根序列指示u分别为25、29、34。由于PSS采用频域Zadoff-Chu序列的方式进行生成，ZC序列具有很好的自相关性，因此同一根序列指示u对应的PSS具有很好的自相关性。将频域的3组PSS补0后进行IFFT变化得到时域的3组本地PSS，和接收的PSS进行相关计算，根据最大值所在的位置以及对应的根序列指示就可以确定PSS定时同步点和。［4］这种算法虽然能够计算出PSS定时同步点的位置和，但是计算量大，复杂度高，同时在接收数据时需要开辟的内存空间较大，最大开辟的空间为153600个字。为了减少计算的复杂度和内存空间问题，对PSS定时同步进行改进。

（1）频域的PSS序列是Zadoff-Chu 序列，由Zadoff-Chu序列的性质可知，该序列具有中心点对称性。通过将频域PSS序列IFFT变换到时域后，发现该序列仍具有良好的对称性。［5］在实际处理中，将时域PSS做成表格进行存储，然后通过直接查表的方式减少计算时域PSS的处理时间。

（2）根据（1）中分析的PSS的性质，在计算PSS定时同步的位置时，采用PSS良好的中心对称性进行相关计算。接收数据PSS同步点的位置确定后，再将本地3组PSS和接收的PSS进行相关计算，确定的值。［6］利用PSS自相关进行定时同步复杂度低，但是当存在频偏时不能保证准确性。

（3）通过分析发现SSS的信号在时域呈现共轭对称性如图2所示，可以利用SSS信号进行自相关来进行定时同步。相关原理与PSS自相关一致，在复杂度上略有改善，但是利用SSS自相关进行定时同步不但复杂度低易于实现而且可以很好的抵制频偏。为进一步减小计算的复杂度，将接收端的数据进行降采样后进行自身的相关计算，降采样后的SSS同步点会存在一定的偏差，偏差和降采样点数有关，在得到粗同步点后在进行精同步这样可以得到SSS的位置。根据SSS同步点的位置可以得到PSS同步点的位置，然后将接收的PSS的数据和本地的3组PSS进行互相关，根据最大值对应的本地PSS可以得到

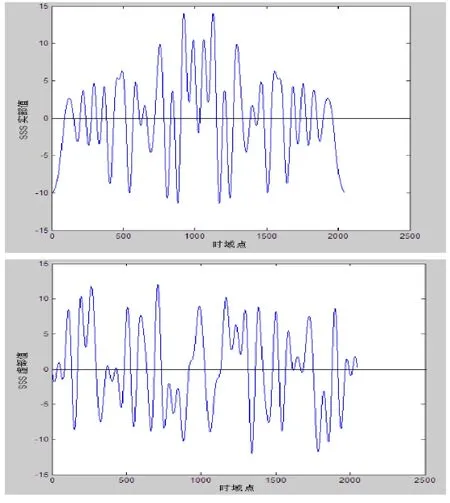
图2　SSS共轭对称性

以下将3种算法进行性能的比较，设发送的信号为s（k），则为归一化频偏k=1,2,3...N -1. PSS自相关计算式为

SSS具有共轭对称性，自相关为计算式为

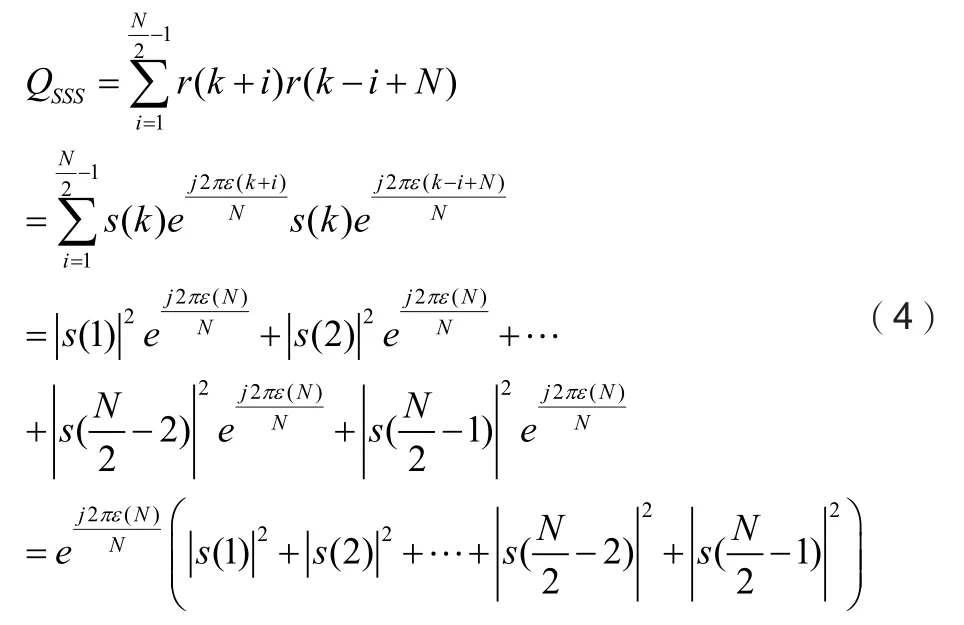
在MATLAB环境下对算法进行仿真分析，AWGN信道换进下，子载波间隔为15kHz，IFFT点数为2048。设归一化频偏ε=1.33，然后计算定时同步点根据3种算法的原理，不同信噪比环境下同步点的均方误差（Mean Square Error）如图3所示，从图3可以看出随着信噪比的增大3种算法的MSE都在减小，但是PSS互相关算法受频偏影响最大基本上可以判断为只要存在大频偏该算法定时同步点计算就会出现错误。PSS自相关算法性能远远不及SSS自相关算法虽然随着信噪比的增大均方误差也在降低。当信噪比大于6dB时SSS自相关算法均方误差为0，即同步点计算正确。

3　实现及仿真

由上述理论分析，可以得到计算SSS定时同步的实现流程图如图4所示。

3.1实现过程

（1）SSS粗同步点的计算。

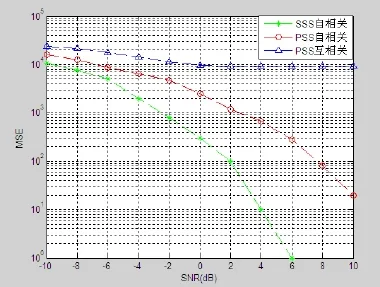
图3　频偏为1.33时同步点的均方误差值

图4　SSS定时同步的实现流程图

为了减小开辟内存空间问题，采用接收数据实时处理，即一边接收数据一边进行相关计算，这就要求在下一次接收数据到来之前需要完成前一次接收数据的处理。在内存中开辟存储空间大小为4096个字，每次接收数据大小为2048。将接收的2048个数据搬移到开辟空间的后2048个字的内存空间中，同时将开辟空间的后2048个字搬移到前2048个字的内存空间，还要设定一个计数器，用于保存SSS粗同步点的值。然后是对将前2048个字内存中的数据中心对称滑动相关计算对称点为1025，为了简化计算在相关计算时采用1/16的降采样，将计算得到的相关操作累加之和和设定的门限值进行比较。如果大于设定的门限，记录相关计算得到最大值所对应的位置，同时加上计数器中的计数值，得到SSS粗同步点的位置，继续SSS精同步点计算；如果小于设定的门限值，则在原来起始位置点向后滑动16个字，再进行1024个字的中心对称滑动相关计算，判断和设定门限的关系，直到找到大于设定门限值为止，记录下该位置为。如果当前2048个字滑动相关计算结束后仍未找到大于设定的门限值，则需要再次接收2048个字的数据，按照以上步骤继续寻找，同时将计数器加2048。

（2）SSS精同步点的计算

通过步骤（1）的计算可以得到SSS粗同步点的位置，这样就可以确定SSS同步点的一个范围。由于降采样为16，所以理论上SSS定时同步点的位置应该在粗同步点之内，为了精确计算，取精同步的计算范围为粗同步点的前后64点作为滑动窗。精同步计算的数据长度为2048+128，不降采样进行128次自相关，根据最大值的位置计算得到精同步点的位置。

根据（2）中SSS同步点可以找到PSS的同步点。将接收的PSS进行1/16降采样和本地的三组PSS降采样后进行互相关，互相关得到最大值对应的PSS就可以得到

3.2复杂度分析：

由于同步信号在上下半帧位置是固定的并且PSS的周期为5ms，在实现时采用半帧153600个数据进行同步点计算。为了简化计算在粗同步中进行了1/16降采样。如下表所示为3种算法的实现复杂度比较，综合粗同步和精同步可以得到，本文方案SSS自相关算法的复杂度远小于PSS互相关定时同步，较PSS自相关算法也有改善。

算法名称　粗同步（循环次数）　精同步（循环次数）PSS互相关　9600*128*3　128*2048 PSS自相关　9600*64　128*1024+8*3*128 SSS自相关　9600*64　128*1024+3*128

3.3仿真结果分析

通过搭建仿真链路对SSS定时同步进行仿真，仿真中采用系统带宽为5MHz，子载波间隔为15kHz，OFDM的子载波数为2048，普通CP，载频2GHz，AWGN信道，发送端发送的小区NID为1，即为为1，时延偏移为0，因为在TDD模式下，SSS映射在时隙1和时隙11的最后一个OFDM符号上，所以在前半帧中理论上SSS定时同步点的计算为30720-2048=28672， 这里从0开始计数，而在matlab仿真时从1开始计数，所以zai matlab仿真时理论上的同步点为28673。仿真结果如下：

由于每次接收2048个点，为了相关计算接收第一组2048时前面一组补0。从图5可以看出相关峰值出现在第16组中，从图6可以看出峰值在第16组2048的第0个位置，所以得到粗同步点为（16-2）*2048+0+1=28673

图5，图6为粗同步计算，由于在粗同步计算中采用了1/16降采样，粗同步点会有误差。为了精确计算，在做精同步取28673前后64点进行自相关，得到峰值的位置后得到SSS精同步点的位置28673-64+64=28673，和理论的位置一致。

根据SSS精同步点的位置可以计算得到PSS的位置，然后和本地3组PSS进行互相关，因为本方案中PSS的点已经固定只需要降采样后直接和本地PSS直接互相关不需要再进行滑动相关。找到3组中的最大值对应的PSS组号就确定了

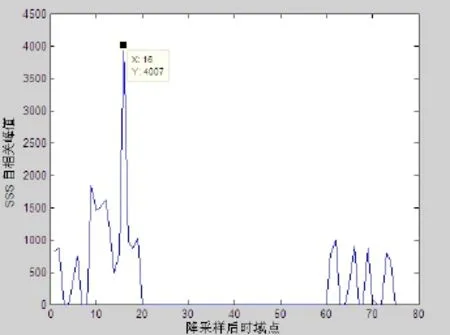
图5　SSS粗同步相关峰值图

图6　SSS粗同步峰值位置图

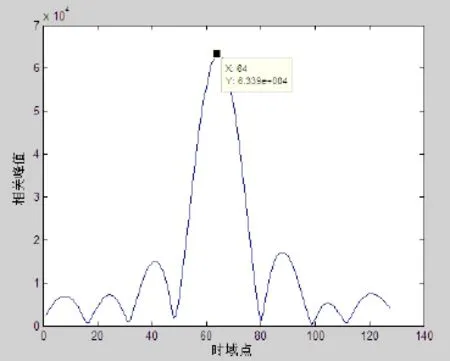
图7　SSS精同步相关峰值图

4　总结

论文通过对已有PSS定时同步算法的研究，结合SSS时域信号的特征，给出了基于SSS定时同步的算法，该算法不但能够很好的抵抗频偏，而且计算复杂度低，易于实现，能够满足LTE-A系统小区搜索算法的性能要求。

1 Stefania Sesia，Issam Toufik and Matthew Baker 《LTE， The UMTS Long Term Evolution From Theory to Practice》，John Wiley & Sons Ltd，2009

2 佟学俭，罗涛.OFDM移动通信技术原理与应用［M］ 北京：人民邮电出版社，2003

3 3GPP TS 36.211 v9.0.0 Evolved Universal Terrestrial Radio Access （E-UTRA）Physical Channels and Modulation（Release 9）［S］. 2009.12

4 盛渊，罗新民.LTE系统中小区搜索算法研究［J］，通信技术，2009，42（3）： 90-92

5 M.M.Mansour， ”Optimized architecture for computing Zadoff-Chu sequences with application to LTE”， in IEEE Global Telecommn. Conf. （GLOBECOM）， Hawaii， HI， 2009

6 W.Xu .and K.Manolakis， “Robust synchronization for 3DPP LTE systems，” in IEEE Global telecommn. Conf. （GLOBECOM）， Miami， FL， 2010

10.3969/j.issn.1006-6403.2016.06.017

（2016-06-01）