基于拟态物理学优化算法的船舶转向避碰决策
2016-10-11于家根刘正江卜仁祥高孝日李伟峰
于家根, 刘正江, 卜仁祥, 高孝日, 李伟峰
(大连海事大学 航海学院, 辽宁 大连 116026)
基于拟态物理学优化算法的船舶转向避碰决策
于家根, 刘正江, 卜仁祥, 高孝日, 李伟峰
(大连海事大学 航海学院, 辽宁 大连 116026)
针对多船会遇态势下的船舶避碰决策难题,提出一种基于拟态物理学优化算法的船舶转向避碰决策方法。该算法将《国际海上避碰规则》相关条款作为约束条件限定问题的可行域空间,同时考虑基于最近会遇距离和航程损失的船舶避碰目标函数,通过迭代进化获取全局范围内的最优解。仿真结果表明:将拟态物理学优化算法应用于船舶转向避碰决策中是可行、有效的,能为船舶驾驶员提供决策支持。
水路运输;拟态物理学优化算法;多船会遇;转向避碰决策
Abstract: The Artificial Physics Optimization (APO) algorithm with the feasible space constrained by The Rules from International Regulations for Preventing Collisions at Sea is introduced into the collision avoidance decision-making in multi-ship encounter situations. The objective function is constructed on the basis of the Distance of the Closest Point of Approach (DCPA) and the voyage losses, and solved through iterative evolution to obtain the optimal solution. The simulation of the process shows that APO algorithm works effectively in determining the course alteration for avoiding collision, therefore, can help marine officers in navigation practice.
Keywords: waterway transportation; APO algorithm; multi-ship encounter; course alteration for collision avoidance
在海上实践中,船舶避碰决策的制定主要依赖于驾驶员的专业知识及其驾驶经验,转向避碰是最常见的行动方案。然而,当船舶处于复杂的多船会遇态势时,驾驶员很难快速给出最佳避碰决策方案,且一旦作出错误决策将导致事故发生。对此,一些学者尝试将进化算法、遗传算法、蚁群算法和粒子群算法等人工智能优化算法应用于船舶避碰决策研究中,已取得一定的成果。[1-4]
拟态物理学优化算法(Artificial Physics Optimization Algorithm,APO Algorithm)[5-6]是一种基于种群的启发式随机搜索算法,同粒子群算法相比,其具有种群多样性好、搜索效率高的优点。这里考虑多船会遇态势下的转向避碰决策,将避碰规则作为行动可行域的约束条件,利用拟态物理学优化算法,从可行域的空间中求出目标函数极小值,进而得到转向避碰决策。
1 船舶避碰决策模型
船舶间会遇并构成碰撞危险时,本船需采取相应的避碰行动进行避让。船舶避碰行动包括转向和变速2种,设其二维解空间为Xi(t)=(xi1(t),xi2(t)),其中:Xi(t)为t时刻问题可行域的第i个解;xi1(t)和xi2(t)分别为该解的航向和航速值。
衡量解的优劣的指标是目标函数,设为f(Xi)=(f1(Xi),f2(Xi),…,fn(Xi)),表示船舶避碰决策同时考虑碰撞危险度和航程损失等多个子目标函数。目标函数取极小值时的解即为最优解。由此,建立船舶避碰决策模型,将船舶避碰决策问题转化为在问题的可行域内使目标函数取极小值的寻最优解问题。
考虑船舶的操纵性能并综合分析转向和变速避让行动的效果,若水域充足,则多采用转向避碰行动,此时解空间由二维简化为一维,即Xi(t)=(xi(t)),其中xi(t)为t时刻第i个解的航向值。考虑《国际海上避碰规则》(以下简称《避碰规则》)对转向避碰的约束,各解的航向值区间为[xmin,xmax],上下边界值根据具体的会遇情况设定。
模型中选取碰撞危险度和航程损失作为子目标函数,其中:碰撞危险度受最近会遇距离DCPA、最近会遇时间TCPA、船舶操纵性能和外界环境等诸多因素的影响,根据研究问题的需要,选取适当的碰撞危险度模型[7-9];航程损失则受转向幅度等因素的影响。
2 基于APO算法的转向避碰决策
2.1APO算法基本原理
APO算法[10-12]是通过模拟物理学原理及其规律而设计的基于种群优化算法的搜索策略。将各个样本解看作是具有质量、速度和位置属性的物理个体,个体的质量是用户定义的与其目标函数值(适应值)相关的函数,个体的适应值越好,质量和个体间的虚拟作用力就越大。适应值较好的个体吸引适应值较差的个体,适应值较差的个体排斥适应值较好的个体,适应值最好的个体则不受其他个体的吸引或排斥。利用这种虚拟力作用规则更新种群个体的位置,通过迭代进化使整个种群向更好的搜索区域移动,进而得到满意的最优解。
2.2避碰目标函数
2.2.1碰撞危险度目标函数
多船会遇转向避碰情况下的碰撞危险度模型较多,必须根据所研究问题的需要进行选取。最小DCPA目标船的DCPA值越大,危险度就越低。因此,设碰撞危险度目标函数为
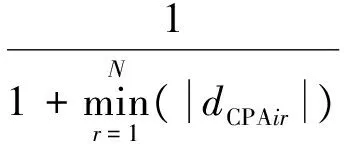
(1)
式(1)中:f1(xi)为种群中第i个个体的碰撞危险度函数值,其值域为(0,1];dCPAir为第i个个体与第r个目标船的最近会遇距离;N为目标船数。目标函数值越小,则第i个个体对所有目标船的最近会遇距离的绝对值的最小值就越大,碰撞危险度越小。
2.2.2航程损失目标函数
避碰实践中,考虑到《避碰规则》对避碰行动 “大幅度”的要求,航向变化角至少为30°[13];考虑到要减小航程损失,要求转向幅度尽可能小。因此,设航程损失目标函数为
f2(xi)=(xi-30)/150
(2)
式(2)中:f2(xi)为种群中第i个个体的航程损失目标函数值,其值域为[0,1];xi∈[30,180]。目标函数值越小,则转向幅度和航程损失就越小。
上述2个目标函数的值域均在[0,1]内,若对这2个子目标分配权重7:3,则多目标函数可简化为以下单目标函数。
f(xi)=0.7f1(xi)+0.3f2(xi)
(3)
2.3种群初始化
设种群数为Npop,Xi(t)=(xi(t))为种群中第i(i∈1,2,…,Npop)个个体在第t代的位置向量(即船舶转向避碰决策中的航向值);设Vi(t)=(vi(t))为个体i在第t代的速度向量(即航向值更新的步长)。在位置约束[xmin,xmax]和速度约束[vmin,vmax]内随机初始化种群。计算初始状态下种群中所有个体的适应值,从中选出最优个体及其适应值。
2.4个体进化
2.4.1个体质量函数计算
(4)
式(4)中:f(xbest)为当前代内最优个体的适应值;f(xworst)为当前代内最差个体的适应值。该质量函数满足2个性质:值域为(0,1],且mbest=1;函数为非负单调有界函数。
2.4.2个体所受合力计算
(5)
(6)
式(5)~式(6)中:Fij为第j个个体对第i个个体的虚拟作用力;rij=xj-xi为个体i到个体j的距离;G为引力常数,可通过选择参数G来控制种群中作收敛运动和发散运动的个体的数量[14];Fi为个体i所受的虚拟作用力的合力;式(5)中,∀i≠j,i=best;式(6)中,∀i≠best。
2.4.3个体位置更新公式
种群个体在其所受虚拟作用力的合力作用下运动。个体在合力方向上的步长决定着其下一代的位置。最优个体不受外界引力的影响,进化中直接传递到下一代。除最优个体之外,任意个体i在第t+1代每一维的速度和位置进化方程如下。
(7)
式(7)中:a为服从(0,1)正态分布的随机变量,即a~N(0,1);w为惯性权重,且w∈(0,1);∀i≠best。
2.5APO算法步骤
1) 初始化参数Npop,G,vmin,vmax,xmin及xmax;计数器t=0;最大迭代代数为tmax。
2) 随机初始化种群:个体位置和速度。
3) 计算种群中所有个体的适应值(式(1)~式(3));选出最优个体Xbest及其适应值f(Xbest),最差个体Xworst及其适应值f(Xworst)。
4) 计算种群中所有个体的质量(式(4))。
5) 计算种群中各个个体所受虚拟作用力的合力(式(5)和式(6))。
6) 更新种群个体的位置(式(7))。
7) 计算更新位置之后种群中所有个体的适应值,更新最优个体Xbest及其适应值f(Xbest)。
8) 判断是否满足结束条件。若满足,则停止计算,输出最优个体Xbest及其适应值f(Xbest);若不满足,则进化代数t=t+1,返回至步骤“4)”。
3 实例仿真分析
3.1仿真实例
设本船的初始航向为000°,航速为15 kn;能见度不良且不在互见中;同时有5艘船舶(分别命名为TS1,TS2,TS3,TS4,TS5)会遇,存在碰撞危险。本船与目标船的会遇态势见表1,其中:DCPA为正值表示目标船过本船艏部;DCPA为负值表示目标船过本船艉部。
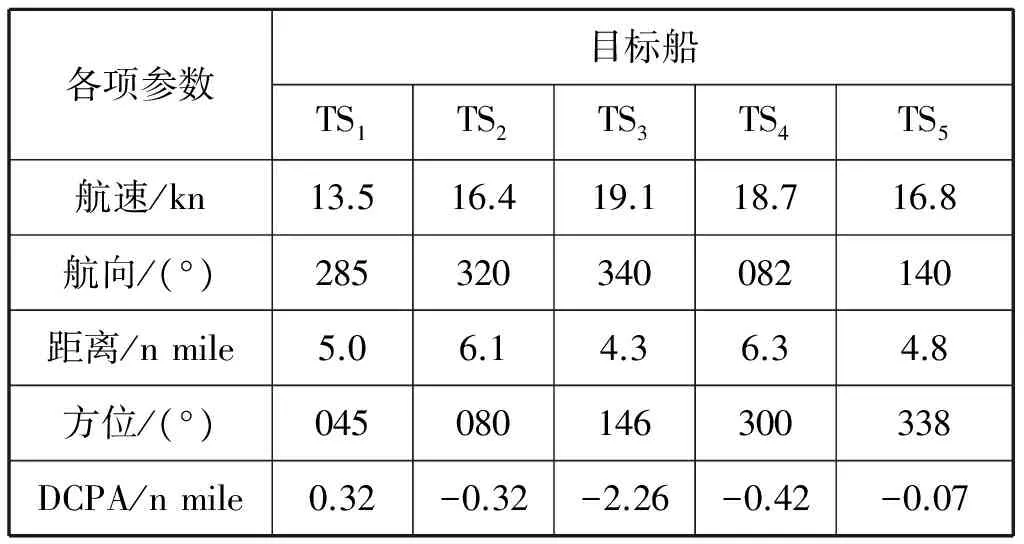
表1 本船与目标船的会遇态势
根据《避碰规则》第19条“船舶在能见度不良时的行动规则”中的第4款“转向”要求的规定并考虑避碰“大幅度”的要求,将种群中个体位置的边界设置为xi∈[30,180]。考虑到转向避碰决策航向值的精度,设置种群中个体的速度边界为vi∈[-1,1]。种群数量设置为50个,即Npop=50。为更好地验证算法的收敛性,设置迭代代数为2 500代。引力常数G取0.1,惯性权重w的计算表达式[6]265为
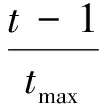
(8)
式(8)中:t为当前代数;tmax为最大循环代数。
3.2结果分析
仿真结果见图1和图2,其中:图1为各代个体的最优值,即船舶转向避碰决策应驶的最佳航向;图2为各代最优个体的适应值。
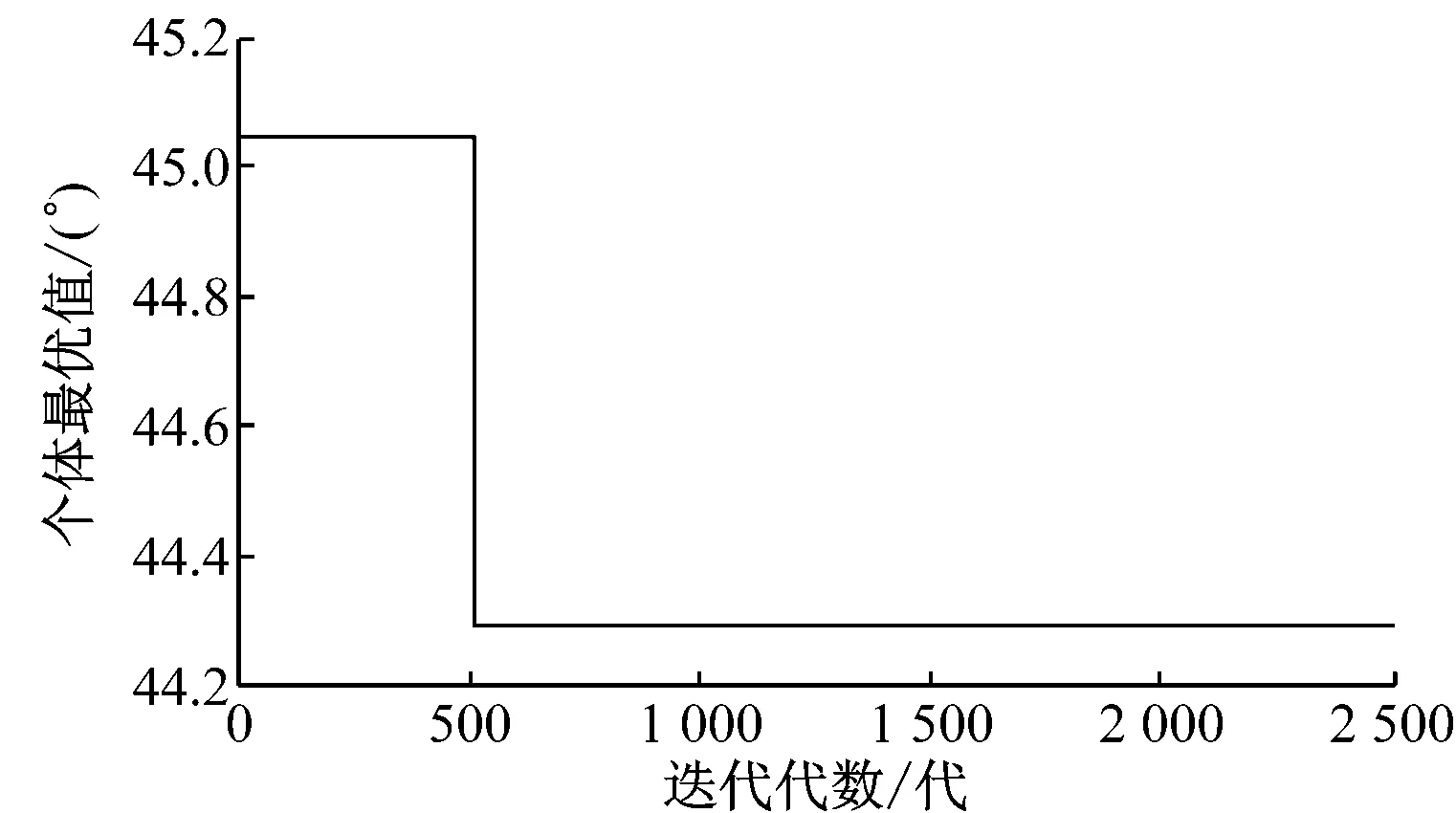
图1 各代个体的最优值
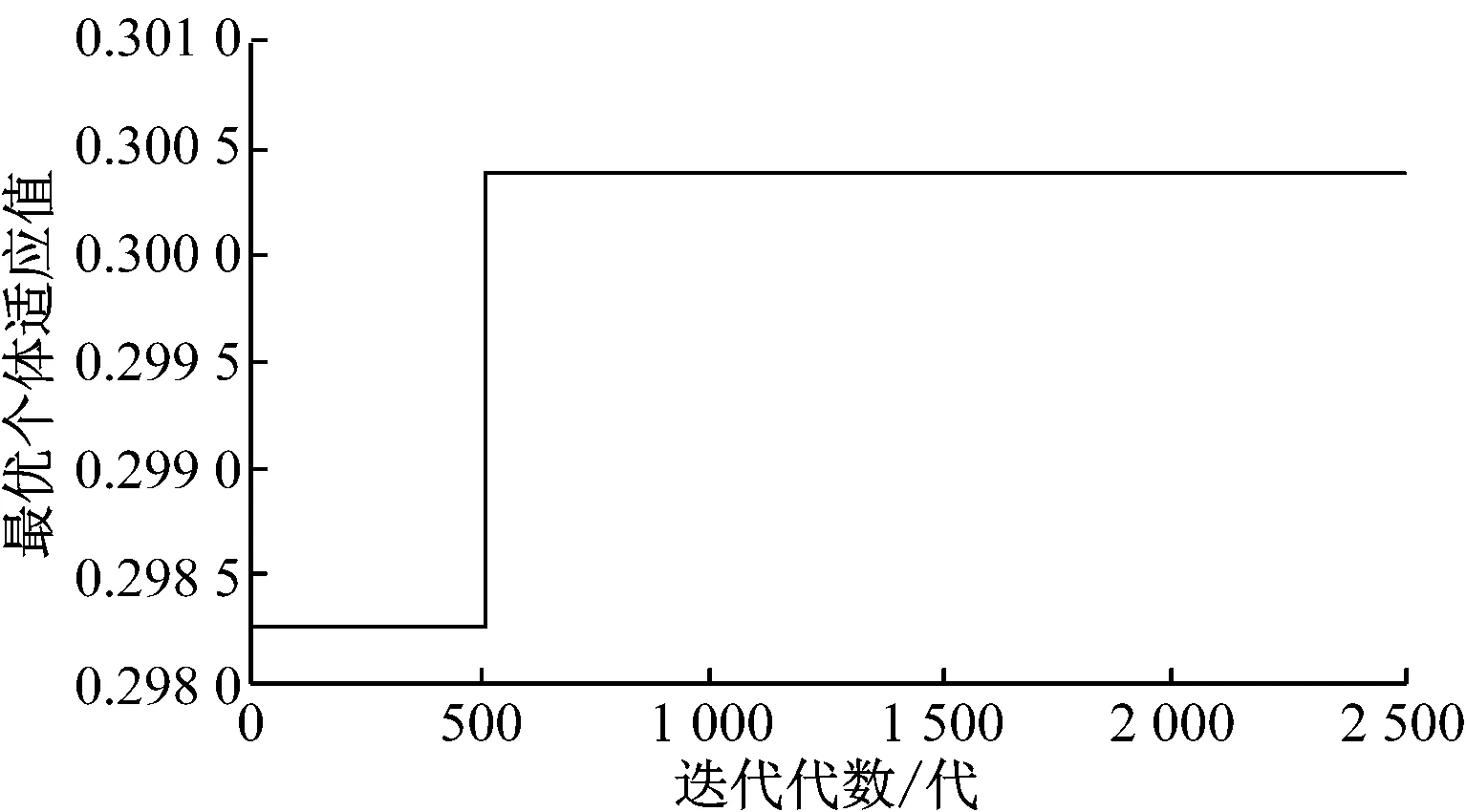
图2 各代最优个体的适应值
由图1和图2可知,结果最终收敛于某个固定值,500代内即趋于稳定,收敛速度快,算法执行耗时5~8 s,能快速给出转向避碰决策。为验证该算法的可行性和有效性,执行30次运算,得到个体最优值的范围为[42.0,46.5],最优个体适应值的范围为[0.295 8,0.309 0],说明该算法能获得满意的一致最优解。
结果表明,本船在该会遇态势下应驶向的最佳航向角为44.3°(30次运算均值),对应的适应值为0.300 4。该航向下,本船对各船(按TS1~TS5的顺序)的DCPA值向量为(2.338 5,1.575 7,-2.343 2,-1.664 8,-1.737 1),结果较为满意。
4 结束语
当船舶间处于会遇态势并有碰撞危险时,多采取转向避碰决策;而当多船会遇时,局面较为复杂,对驾驶员的专业技能和经验有较高要求,一旦决策失误将导致碰撞事故发生。对此,在建立的船舶避碰决策模型的基础上提出基于拟态物理学优化算法的船舶避碰决策方法,旨在利用APO算法的快速全局寻优能力为船舶驾驶员提供决策支持。针对多船会遇的复杂局面,考虑《避碰规则》的约束限制,建立基于最近会遇距离的避碰目标函数,通过迭代进化获取最佳决策方案。结果表明:该算法可行、有效,能为船舶驾驶员提供决策支持。
[1] SMIERZCHALSKI R, MICHALEWICZ Z. Modeling of Ship Trajectory in Collision Situations by an Evolutionary Algorithm[J]. IEEE Transactions on Evolutionary Computation, 2000, 4(3): 227-240.
[2] TSOU Mingcheng, KAO Shenglong, SU Chienmin. Decision Support from Genetic Algorithms for Ship Collision Avoidance Route Planning and Alerts[J]. Journal of Navigation , 2010, 63(1): 167-182.
[3] JOSE B E, JUAN F J, JOSE M G S. Optimization of Autonomous Ship Maneuvers Applying Ant Colony Optimization[J]. Expert Systems with Applications, 2012, 39(11) : 10120-10139.
[4] 王得燕, 刘以安. 粒子群算法在多船避碰决策中的应用[J]. 计算机工程与设计, 2009, 30(14): 3380-3382.
[5] 谢丽萍,曾建潮. 基于拟态物理学方法的全局优化算法[J]. 计算机研究与发展, 2011, 48(5):848-854.
[6] 曾建潮,崔志华. 自然计算[M].北京:国防工业出版社,2012:246-265.
[7] TAM C K, BUCKNALL R. Collision Risk Assessment for Ships[J]. Journal of Marine Science and Technology, 2010, 15(3): 257-270.
[8] 郑中义, 吴兆麟. 船舶碰撞危险度新模型[J]. 大连海事大学学报, 2002, 28(2): 1-5.
[9] 刘茹茹,胡勤友. 一种主观的船舶碰撞危险度评价模型[J]. 上海海事大学学报, 2012, 33(1): 41-44.
[10] XIE Liping, TAN Ying, ZENG Jianchao. The Convergence Analysis of Artificial Physics Optimization Algorithm[J]. International Journal of Intelligent Information and Database Systems, 2011, 5(6): 536-54.
[11] XIE Liping, TAN Ying, ZENG Jianchao. Artificial Physics Optimization: A Brief Survey[J]. International Journal of Bio-Inspired Computation, 2010, 2(5): 291-302.
[12] XIE Liping,TAN Ying, ZENG Jianchao. The Selection Strategy of Mass Functions in Artificial Physics Optimization Algorithm[J]. International Journal of Modeling, Identification and Control, 2013, 18(3): 226-233.
[13] ZHAO Yuelin. Collision Avoidance and Watch Keeping[M]. Dalian: Dalian Maritime University Press, 2010:101-102.
[14] 王艳. 多目标拟态物理学优化算法及其应用研究[D]. 兰州: 兰州理工大学, 2011.
Collision-AvoidingCourseAlterationOptimizationwithArtificialPhysicsAlgorithm
YUJiagen,LIUZhengjiang,BURenxiang,GAOXiaori,LIWeifeng
(Navigation College, Dalian Maritime University, Dalian 116026, China)
2015-11-12
国家自然科学基金(51379026);中央高校基本科研业务费专项资金(3132016002;3132013004;3132013005;3132013015)
于家根(1984—),男,黑龙江绥化人,讲师,博士生,研究方向为船舶智能避碰。E-mail:yujiagen@dlmu.edu.cn 刘正江(1959—),男,江苏如皋人,教授,博士生导师,研究方向为海上交通安全。E-mail:liuzhengjiang@dlmu.edu.cn
1000-4653(2016)01-0036-03
U675.96
A
