散粒体斜坡失稳破坏内部因素试验研究

卜祥航，傅荣华，李仅德，黄　友

(1. 成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都　610059；2.四川省煤田地质工程勘察设计研究院　成都　610059；3. 武汉一冶钢结构有限责任公司　 武汉　 430080)



散粒体斜坡失稳破坏内部因素试验研究

卜祥航1，傅荣华1，李仅德2，黄友3

(1. 成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都610059；2.四川省煤田地质工程勘察设计研究院成都610059；3. 武汉一冶钢结构有限责任公司 武汉 430080)

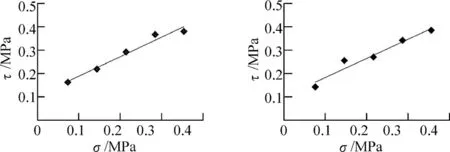
影响散粒体斜坡稳定性的诸多因素中，外部因素起到诱导作用，内部因素则起到主导作用，其中天然休止角对散粒体斜坡的稳定性起到控制作用。故配制4种不同级配样品(1

散粒体斜坡; 多元线性回归理论;休止角;影响因素;估算模型

1　研究背景

散粒体斜坡是指由于风化作用，高陡斜坡形成以碎石、角砾为主的砂粒和碎屑，在重力和构造运动下发生溜动，并在坡脚以天然休止角堆积[1]。不仅是交通运输的重大隐患，而且是泥石流的重要物质来源。国外对散粒体斜坡的研究始于1938年，提出了碎屑溜的概念[2]，随后研究其自组织临界性，并以此为基础探索坡体失稳破坏的动力学机制[3-11]。国内起步于20世纪90年代，1995年罗德富提出溜砂坡的概念[11]，而后国内学者以地质灾害的角度，探索其演化规律、失稳诱发因素以及颗粒运动特征等[12-16]。

野外调查发现，散粒体斜坡堆积体愈接近其天然休止角，坡体的稳定性愈差，即使很小的扰动，都可导致坡体的失稳。Caine[3]认为散粒体斜坡失稳原因主要为地震及大范围降水；吴国雄等[14]研究溜砂坡失稳的条件，得出颗粒的粒径、含水量是影响天然休止角的重要因素，但未考虑颗粒浑圆度、粗细颗粒混杂程度、颗粒不均匀度对休止角的影响。张元才[12]、李川[16]考虑了以上因子对休止角的影响，但是并未建立休止角的估算模型。影响散粒体斜坡天然休止角的内部因素很多，且多未有实验验证。故本文选取散粒体斜坡失稳的相关内部因素，分析它们对散粒体斜坡坡体稳定性的影响，探索适合类似地质环境的散粒体斜坡天然休止角的估算模型。

2　失稳破坏内部因素试验设计

散粒体斜坡稳定性很大程度上取决于其天然休止角。根据散粒体斜坡特点和前人研究成果，选取颗粒浑圆度、粗细颗粒混杂程度、颗粒不均匀度和颗粒的抗剪参数(c,φ)5个内部因子，分析它们与天然休止角间的关系，建立天然休止角估算模型。

2.1试验模型

野外调查典型散粒体斜坡堆积体高度约80m，原地面坡度约35°，因室内试验场地的限制,试验台模型的比例设计为1∶100。试验在一个高50cm，宽50cm，长90cm(图1)的木制模型架中进行，槽内用一块粗糙木板(1.4m×0.5m)模拟野外原地面。在斜坡顶部(模拟砂源区)人工加颗粒，在斜面底部自由堆积(模拟堆积区)，利用激光测距仪测出颗粒堆积体的角度，即为天然休止角。

尺寸单位：mm图1　试验模型Fig.1　Sketch of the test model

2.2试验材料

本试验所采用的材料取自汶川县绵虒镇簇头沟散粒体斜坡，不均匀系数Cu约为7，曲率系数Cc约为1.16，见图2。由于试验模型及室内试验所限，粒径小于5mm的颗粒为细颗粒[17]，粒径在5～20mm的颗粒为粗颗粒，配制三组不同级配(Cu=1,2.5,3.4,7)样品，共12个。典型样品颗粒级配见表1。

图2　试验材料级配曲线Fig.2　Gradation curve of test material表1　典型样品颗粒级配(累积百分含量)Table 1　Grain size distribution of typical samples(cumulative percentage)

样品编号小于某粒径累计百分含量/%0.25mm0.5mm1mm2mm5mm10mm20mmCu1#———————1.02#1351060801002.53#1351048751003.44#13102051701007.0

注：1#样品粒径为2～5mm

3　试验成果及分析

3.1试验成果

浑圆度是颗粒磨圆程度的首选指标[13]，其计算公式如式(1)所示，即

(1)

式中：ri为某个尖角的半径；R1为颗粒最大内接圆半径；n为颗粒尖角总数。

粗细颗粒混杂度用粗细颗粒质量之比m来表示，即试样中粗颗粒质量与细颗粒质量的比值。

天然状态下散粒体斜坡只受到重力场的作用，为尽量与实际相符，中剪试验中正压力的取值分别为0.1，0.2，0.3，0.4，0.5MPa。图3为典型样品的中剪试验抗剪强度曲线。

(a)1#样品　　　　　　　　　　　(b)2#样品

(c)3#样品　　　　　　　　　　　(d)4#样品图3　典型样品的τ-σ曲线Fig.3　Curves of τ-σ of typical samples

根据库伦定律可得式(2)，从而得出样品的力学参数。剪切过程中，颗粒间某些咬合点被切断或磨损，这是产生黏聚力的主要原因。

τf=c+σtanφ。

(2)

式中：τf为抗剪强度；c为黏聚力；σ为总应力；φ为内摩擦角。

通过以上方法即可获得样品的物理力学5个参数的值，见表2。

表2　内部失稳因素参数汇总Table 2　Summary of parameters of internal instabilityfactors

3.2颗粒不均匀程度对休止角θ的影响

不均匀系数与休止角间的函数关系如下：

θ=0.02Cu2+0.27Cu+37.42， R2= 0.99。

(3)

颗粒的不均匀系数对其休止角的影响如图4(a)所示：休止角的大小随颗粒不均匀系数的增大而增大。由于不均匀系数较大的样品中粒径分布广泛，大颗粒形成系统骨架，小颗粒充填于大颗粒形成的孔隙中，大小颗粒相互填充较充分，颗粒间作用点的数目得到了增加，咬合能力较强，密实程度得到了提高，堆积体的休止角增大，体系抗外界扰动能力增强。

(a)不均匀系数

(b)浑圆度

(c)参数m图4　不均匀系数、浑圆度和参数m与休止角的关系Fig.4　Relations of angle of repose to non-uniformcoefficient,round degree,and parameter m

3.3颗粒浑圆度对休止角的影响

颗粒浑圆度与休止角间的关系如图4(b)所示，函数关系如下：

θ=11.94R12-28.46R1+54.91，R2= 0.83。

(4)

休止角的大小随浑圆度的增大有增大的趋势，浑圆度在1.14～1.40之间，休止角的增长速率较低，浑圆度达到1.4以后增长速率较高。张元才[12]曾以玻璃球为实验材料，玻璃球浑圆度约1.13，其堆积体的休止角为27.83°。与本文中9#样品作对比，浑圆度相差0.01，而休止角却相差约10°。分析颗粒间运动过程中能量摩擦耗散过程可知9#样品颗粒较玻璃球表面凹凸性强，颗粒间的摩擦路径更为曲折、复杂，能量摩擦耗散较大，颗粒运动加速过程减缓，同时可避免颗粒的冲击，更有利于堆积体的稳定。

3.4颗粒粗细颗粒混杂程度对休止角的影响

粗细颗粒混杂程度与休止角间的关系如图4(c)所示，函数关系如下：

θ=-5.15m2+8.28m+36.68，R2= 0.83。

(5)

休止角的大小随m值先增大后减小，而后趋于稳定。m值在0～0.81之间，休止角逐渐增大，m达到1以后逐渐减小而趋于稳定。其主要原因是m 较小时，堆积体的休止角受控于细颗粒，而m较大时，堆积体的休止角受控于粗颗粒。粗颗粒含量较少时(m<1)，粗颗粒之间不能有效接触，无法形成骨架结构，此时样品级配较差，堆积体的休止角较低。m在1附近时，粗颗粒即可起到骨架结构作用，细颗粒又可有效充分地填充粗颗粒间的空隙，从而达到堆积体的最佳稳定效果，休止角达到最高。粗颗粒含量继续增加(m>1)，堆积过程中细颗粒体积小于粗颗粒间提供的空隙，从而构成不稳定的骨架，堆积体休止角降低而趋于稳定。

3.5颗粒抗剪参数对休止角的影响

颗粒c，φ与休止角间的函数关系如下：

θ=265.45c2-17.05c+38；

(6)

θ=0.49φ2-36.98φ+738.41。

(7)

由图5可知，堆积体的休止角整体上随c，φ的增大而增大，但在起初阶段变化较为缓慢。

(a)内摩擦角与休止角曲线

(b)黏聚力与休止角曲线图5　内摩擦角、黏聚力与休止角的关系曲线Fig.5　Curves of angle of repose vs. internal friction angle,and angle of repose vs. cohesion

散粒体的物理力学性质包含2部分[16]。一是散粒体颗粒间的滑动，产生的滑动摩擦；二是散粒体颗粒与颗粒间克服咬合而移动，从而产生咬合联结。其中滑动摩擦是由于颗粒接触面粗糙不平，形成微细咬合而产生的。咬合摩擦是由于相邻颗粒对彼此之间的相对移动起约束作用而形成的。

假设将颗粒放置于每边与其相切的长方体中，3条边表示该颗粒在三维坐标中的大小。长、宽、高分别称为颗粒的三轴径，用来比较散粒体颗粒的大小，见图6。由表2可知，当粒径较小时，散粒体颗粒的力学性质会较低。m越小，散粒体细颗粒越多，粒径越小，其三轴径相差就越小，突角也会相对更加短小，颗粒间的接触面积减小，咬合程度降低，滑动摩擦角和咬合摩擦角就会较小。在受到挤压和剪切作用而使颗粒间相对运动时，要克服的摩擦阻耗较小，颗粒间相对滑动比较容易。因此一定范围内(c<0.06，φ<38.3°)，随着c，φ的增加，堆积体休止角的变化不明显。

图6　散粒体颗粒的三轴径Fig.6　Triaxial diameters of granular particle

而随着颗粒粒径的增大，相邻散粒体间的接触面积也会增大，在受到剪切作用情况下，颗粒间相互移动时有滑动摩擦的面积增大，相应的滑动摩擦角会有一定程度的增长，而且此时相邻颗粒对彼此之间的相对移动起到的约束作用会有明显增强，颗粒要跨过阻碍它的相邻颗粒继续运动就会更加困难，其角度和高度的起伏差会很大，剪胀效应明显，如果要剪断散粒体颗粒，其所需的力就越大。因此,随着散粒体颗粒粒径的加大，其表现出来的物理力学性质会增强，堆积体的休止角亦会增加。

最后运用多元线性回归分析[18]，结合以上数据分析，建立散粒体斜坡的Cu在1～7之间，自然休止角估算模型：

θ=0.37Cu+0.13R1+0.019m+1.24c+

0.067φ+34.48,R2= 0.96。

(8)

采用已获得的实验数据[16](表3)来验证本文自然休止角估算模型的准确性。将表3中的参数代入式(8)中，得出堆积体的休止角为37.66°，与实验测得的休止角37.69°仅相差0.03°。另外将上文中提到的茂县洼底乡散粒体斜坡砂样相关数据：Cu=7，浑圆度为1.56，m=1.05，c=0.08kPa,φ=38.2°，代入式(5)中，得出休止角为39.95°，较现场测得天然休止角38°大1.95°，在可接受范围内。以上说明此估算模型可以根据内部影响因素的参数值来近似估计散粒体斜坡的天然休止角。

表3　验证实验数据Table 3 Verification of test data

4　结　论

本文通过自制模型架，模拟颗粒自由堆积，并测得实验堆积体的天然休止角。分析颗粒浑圆度、粗细颗粒混杂程度、颗粒不均匀度和颗粒抗剪参数(c,φ)5个内部因子与堆积体天然休止角的关系，得出以下结论：

(1)休止角的大小随颗粒不均匀系数的增大而增大。得出堆积体天然休止角与颗粒不均匀系数的关系式。

(2)休止角的大小随浑圆度的增大有增大的趋势，浑圆度在1.14～1.4之间，休止角的增长速率较低，浑圆度达到1.4以后增长速率较高。得出堆积体天然休止角与颗粒浑圆度的关系式。

(3)休止角的大小随m值增大先增大后减小，而后趋于稳定。m值在0～0.81之间，休止角的变化最大，m达到1以后逐渐减小而趋于稳定。得出堆积体天然休止角与粗细颗粒混杂程度的关系式。

(4)堆积体的休止角整体上随c,φ的增大而增大，但在起初阶段(c<0.06kPa,φ<38.3°)变化较为缓慢。分别得出堆积体天然休止角与c,φ的关系式。

(5)最后运用多元线性回归分析，结合数据分析，建立散粒体斜坡Cu在1～7之间，自然休止角估算模型：θ=0.37Cu+0.13R1+0.019m+1.24c+0.067φ+34.48 。并通过与他人实验数据和野外调查采集的数据进行验证，证明了估算模型的准确性,为散粒体斜坡的防治工程设计提供参考依据。

由于实验模型的局限性，本文实验材料平均粒径较实际小很多，不能完全与实际相吻合。因此将来此方面的研究应加大模型尺寸及实验材料粒径，提高实验的精准度。

[1]卜祥航.散粒体斜坡地质灾害挡排固砂工程防治技术研究[D].成都：成都理工大学，2013.

[2]BLONGRJ.ANumericalClassificationofSelectedLandslidesofDebrisSlide[J].EngineeringGeology,1973,7(2):341-359

[3]CAINEN.TheRainfallIntensity-DurationControlofShallowLandslidesandDebrisFlows[J].GeografiskaAnnaler,1980,62(1/2):23-27.

[4]CLARKGM.DebrisSlideandDebrisFlowHistoricalEventsintheAppalachiansSouthoftheGlacialBorder[J].ReviewsinEngineeringGeology,1987,7:125-138.

[5]BRUNSDEND,CHANDLERJ.DevelopmentofanEpisodicLandformChangeModelBasedupontheBlackVenMudslide[M]∥BROOKSSM,ANDERSONMG.AdvancesinHillslopeProcesses.Chiehester:Wiley&Sons,1996.

[6]GABRIELSD.TheEffectofSlopeLengthontheAmountandSizeDistributionofErodedSiltLoamSoils:ShortSlopeLaboratoryExperimentsonInterrillErosion[J].Geomorphology,1999,28(1/2):169-172.

[7]BAKP,TANGC,WIESENFELDK.Self-organizedCriticality:AnExplanationofl/fNoise[J].PhysicalReviewLetters,1987,59(4):381-384.

[8]HELDGA,SOLINADH,KEANEDT,et al.ExperimentalStudyofCritical-massFluctuationsinanEvolvingSandPile[J].PhysicalReviewLetters,1990,65(9):1120-1123.

[9]FRETTEV,CHRISTENSENK,MALTHE-SORENSSENA,et al.AvalancheDynamicsinaPileofRice[J].Nature,1996,379(27):49-52.

[10]BRETZM,CUNNINGHAMJB,KURCZVNSLCIPL,et al.ImagingofAvalanchesinGranularMaterials[J].PhysicalReviewLetters,1992,69(1):2431-2434.

[11]ROSENDAHLJ,VEKICM,KELLEYG.PersistentSelf-organizationofSandPile[J].PhysicalReview,1993,47(2):1401-1404.

[12]张元才.天山公路散粒体边坡形成机理及防治对策研究[D].成都：成都理工大学，2008.

[13]尚彦军，杨志法，廖秋林,等.雅鲁藏布江大拐弯北段地质灾害分布规律及防治对策[J].中国地质灾害与防治学报，2001，12(4):34-35.

[14]吴国雄，曾榕彬，王成华.溜砂坡的形成诱发因素及失稳破坏条件[J].中国铁道科学，2006，27(5):7-12.

[15]卜祥航，傅荣华，李宁.散粒体斜坡注浆固坡工程防治技术实验研究[J].工程地质学报，2015,23(3):415-420.

[16]李川.散粒体斜坡破坏评价方法研究 [D].成都：成都理工大学，2013

[17]孙业志.振动场中散体的动力效应与分形特征研究[D].长沙：中南大学，2002.

[18]徐建华.地理系统分析[M].兰州：兰州大学出版社，1991.

(编辑：赵卫兵)

Internal Factors of the Failure of Granular Mixtures Slope

BU Xiang-hang1，FU Rong-hua1，LI Jin-de2，HUANG You3

(1.StateKeyLaboratoryofGeohazardPreventionandGeoenvironmentProtection,ChengduUniversityofTechnology,Chengdu610059,China; 2.SichuanCoalFieldGeologicalEngineeringSurvey,DesignandResearchInstitute,Chengdu610059,China; 3.WuhanSteelStructureCo.Ltd.ofChinaFirstMetallurgicalGroup,Wuhan430080,China)

Amongfactorswhichaffectthestabilityofgranularmixturesslope,externalfactorsplayaninducingrolewhileinternalfactorsdominate,butthenaturalangleofreposeoftheslopeplaysacontrollingrole.Inviewofthis,granularmixturematerialsoffourdifferentcompositions(1

granularmixturesslope;multiplelinearregressiontheory;angleofrepose;influencefactor;estimationformula

2015-07-27;

2015-09-19

国家自然科学基金资助项目(41072228)

卜祥航(1987-)，男，江苏徐州人，硕士研究生，主要从事岩土体稳定性及工程环境效应研究工作，(电话)13402803918(电子信箱)309351649@qq.com。

10.11988/ckyyb.20150606

2016,33(09):116-120

TU413.6

A

1001-5485(2016)09-0116-05