磨床用自定心中心架的机构设计与优化
2016-10-10赵永强王耀锋侯红玲
赵永强 王耀锋 侯红玲
陕西理工大学,汉中,723001
磨床用自定心中心架的机构设计与优化
赵永强王耀锋侯红玲
陕西理工大学,汉中,723001
设计了一种磨床用自定心中心架的原型机构,建立了自定心中心架的参数组合和平动凸轮的参数化模型。通过对机构的设计参数组合筛选,提出了机构的优化设计目标和优化函数,设计了优化的计算程序。在保证中心架的传力性能、夹持稳定性和夹持精度的前提下,对机构中平动凸轮的两个重要参数进行了优化,为磨床用高精度自定心中心架的设计提供了完整的设计方案。
自定心中心架;细长轴磨削;平动凸轮;参数化设计
0 引言
细长轴类零件的加工一直以来都是机械工程师的关注焦点,为了提高轴类零件的加工精度,各种不同的加工工艺被引入实际加工中,其中,采用中心架作为辅助支承提高零件的刚度是一种理想的工艺方法。尤其是在超长丝杠和螺杆的磨削过程中,中心架的定心定位精度成为提高零件加工精度的制约因素[1]。
国内对中心架的研究大多停留在传统的设计基础之上,如彭克立等[2]设计了一种高速、超高速磨削的自动跟踪式中心架;孙金海等[3]设计了一种采用V形块自动定心的丝杠自锁夹紧的自动定心中心架;王伟顺等[4]采用静压原理设计了一种重型机床加工大型轴类零件用的高精度重载静压中心架;牛福林等[5]设计了一种采用V形滚轮式夹紧机构、T形丝杠自锁和液压刹紧机构的手动高刚性自定心中心架。以上的研究都存在中心架自动化程度不高、夹紧力调节繁琐、适应性较差等缺点。
早在1960年前后,德国某夹具厂商率先推出了一种自定心中心架。随后瑞典、美国等欧美国家也研制出了多种自定心中心架。此类中心架利用凸轮无穷多精确点的特性,在定位精度和夹持可靠性等方面具有突出优势,因而该类型自定心中心架迄今仍是市场上的主流产品[6-12]。
近些年来,国内针对自定心中心架的研究也取得了一些成果。李京鲁[13]对自定心中心架的楔形凸轮的轮廓曲线进行了理论推导;涂庭波[14]对液压自定心中心架的凸轮机构进行了研究,给出了凸轮设计的方法;卢学玉等[15]对液压自定心中心架凸轮曲线进行了理论推导;肖凯[16]从加工的角度给出了凸轮曲线的求解方法;Wu等[17]和Wang等[18]从液压角度分析了影响中心架的工作压力的因素,并对参数进行了优化。由此可见:国内学者针对自定心中心架的研究主要是围绕凸轮机构的理论计算和液压夹紧力的调节两个方面进行的,而这两个因素正是保证夹持中心恒定和夹持力稳定的两个关键点,其中凸轮轮廓的精确设计与加工是实现夹持中心恒定的前提。
以上对凸轮轮廓的设计多采用包络法、瞬心法、复变量法等。包络法利用凸轮和从动件的几何关系推导出接触点的轨迹方程;瞬心法可同时确定压力角、平面凸轮轮廓和凸轮曲率半径;复变量法可同时求得压力角和曲率半径,但包络法和瞬心法只是近似求解方法,求解过程繁琐,精度不高;复变量法的求解精度高,但是求解方程式比较复杂,关系推导困难[19-20]。
近年来,基于参数化数值求解的解析法在复杂轮廓凸轮设计中的优越性越来越明显,多轴数控铣削加工和CNC成形磨削技术的发展,使复杂轮廓凸轮的设计与加工逐步成熟。笔者设计了一种磨床用自定心中心架,建立了关键零件平动凸轮的数值计算模型,利用参数化设计手段,将平动凸轮与滚轮从动件的压力角、夹持力的周向间隔角度以及摆杆杆长作为约束条件,对自定心中心架机构进行优化设计。考虑自定心中心架系对称结构,故文中涉及的计算及优化设计除特别说明外,均只针对机构中的上半部分进行。
1 自定心中心架的工作原理
自定心中心架机构原理如图1所示。具有对称工作曲线的平动凸轮做左右平移,滚轮1、2、3的结构尺寸相同,滚轮3的中心D固定在平动凸轮的右端,工件的夹持中心始终在O3点。中心架夹紧工件的过程为:在外部驱动力作用下,平动凸轮及滚轮3向右移动,与凸轮接触的两个滚轮4、5受平动凸轮的作用,带动摆杆1、2绕着各自的铰点O1、O2转动,从而带动滚轮1和滚轮2转动,实现对工件的夹紧。在夹持过程中,滚轮1、2、3始终同步运动,同时夹紧或松开工件,从而使被加工工件轴心始终保持在O3位置,以实现中心架对工件的夹持和定心。

图1 自定心中心架的机构原理
在自定心中心架设计中,为了推算平动凸轮的廓形,首先保持机架和被加工工件轴心O3不变,初步设计摆杆1、2的长度,通过改变被夹持工件的半径使摆杆1、2转动,滚轮4、5的中心摆动和滚轮3的移动形成平动凸轮的廓形。中心架的外加驱动力为F0,滚轮1、2、3对工件的夹持力依次为F4、F5、F3。
2 平动凸轮廓形的解析计算
2.1坐标系的建立
自定心中心架的参数定义如图2所示。以摆杆1的轴心O1为原点,以平动凸轮的平移轴为X1轴建立静坐标系O1X1Y1。以平动凸轮的左端面为OYZ平面,以过被夹持工件中心O3的直线为X轴,建立动坐标系OXY,O1X1Y1与OXY之间的Y向距离为L1cosθ,X向距离为L3,则
(1)
L4=L0cos(α+β)
其中,L5为平动凸轮的预设值;Lu为平动凸轮沿X方向的移动距离。

图2 自定心中心架的参数定义
2.2平动凸轮廓形计算
设定摆杆的左摆臂O1A的长度为L0,右摆臂O1C的长度为L2,铰点O1与工件轴心O3的距离O1O3为L1,O1O3与右摆臂O1C的夹角∠O3O1C=α;左右摆臂之间的夹角∠AO1C=φ;滚轮4、5的半径为r,r0为滚轮1、2、3的半径;R为被夹持工件的半径,被夹持工件半径R的最大值记为最大夹持半径Rmax,最小值记为最小夹持半径Rmin,则R∈[Rmin,Rmax];Rmax对应的右摆臂O1C与X轴之间的夹角记为ε。
最大夹持半径Rmax和最小夹持半径Rmin对应的右摆臂O1C与O1O3之间的夹角分别记为αmax和αmin,则
(2)
(3)
滚轮1的中心C与工件中心O3之间的距离
(4)
工件中心O3与摆杆1、2的铰点O1、O2的连线之间的夹角∠O3O1O2=θ,其值为
(5)
左摆臂O1A在最高位置时与X轴之间的夹角记为β,其值为
(6)
如图3所示,被夹持工件的半径从Rmin变化至Rmax时,滚轮4的中心A从A1移动至A2,同时平动凸轮向左平移的距离
Lu=Lx-(L1-L2)
(7)
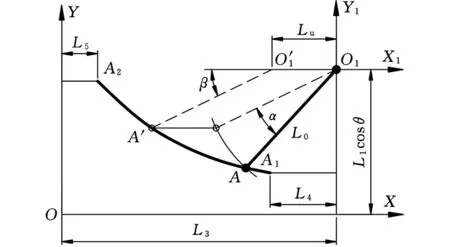
图3 凸轮上A点坐标计算
当被夹持工件的半径R最大时,β=βmax,滚轮4的中心A处于A1点,可推算
L4=L0cosβmax
(8)
在O1X1Y1坐标系中,滚轮4的中心点A的坐标xA、yA为
(9)
根据平动凸轮的理论廓线,基于包络法可求解得到平动凸轮的实际廓形坐标:
(10)
y1=L0cos(α+β)
将x0、y0从坐标系O1X1Y1变换到坐标系OXY中即可得到凸轮的最终廓线方程:
(11)
3 主要参数计算
在自定心中心架中,初始参数选择不当会导致凸轮轮廓设计不合理,机构不能实现预期的功能,或者运行中的动力学特性欠佳。根据平动凸轮廓形计算过程推导和前期的预验算,选择自定心中心架中平动凸轮的压力角和影响夹持质量的夹持力间隔角度两个参数分别进行分析计算[21-22]。
3.1平动凸轮的压力角
如图1和图2所示,设α1为凸轮实际廓线的法线n-n与水平线之间的夹角,则
(12)
设β1为凸轮对滚轮4的力作用线n-n与左摆臂之间的夹角:
β1=α1-π/2-α+ψ-θ
(13)
滚轮1对工件的压力作用线与水平轴线之间的夹角
(14)
滚轮1对工件的力作用线与右摆臂之间的夹角
(15)
平动凸轮的压力角
α1=π/2-β1
(16)
当被夹持工件的半径变化时,可以得出平动凸轮压力角的变化趋势,如图4所示。从图4可以看出,平动凸轮的压力角随被夹持工件半径的增大而增大,近似成线性比例关系。
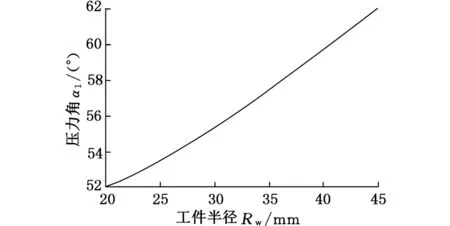
图4 工件半径与平动凸轮压力角的关系
3.2夹持力周向间隔角
夹持力周向间隔角定义为摆动夹持滚轮1(或2)对工件的夹持力F4(或F5)与滚轮3对工件的夹持力F3之间的夹角,其值为
φ=π-δ1
(17)
在自定心中心架夹持工件时,滚轮1、2、3的三个中心C、E、D,滚轮与工件的切点和工件的夹持中心O3之间都是相互共线的,并且与各夹持力的作用线相重合。改变工件半径之后夹持力周向间隔角变化如图5所示,三个夹持力随被夹持工件半径和夹持力轴向间隔角的变化如图6和图7所示。在图7中,工件未受切削力作用,φ越趋近120°,三个夹持滚轮对工件的夹持力在数值上越接近,中心架的夹持越稳定,夹持质量越好。

图5 工件半径与夹持力周向间隔角的关系
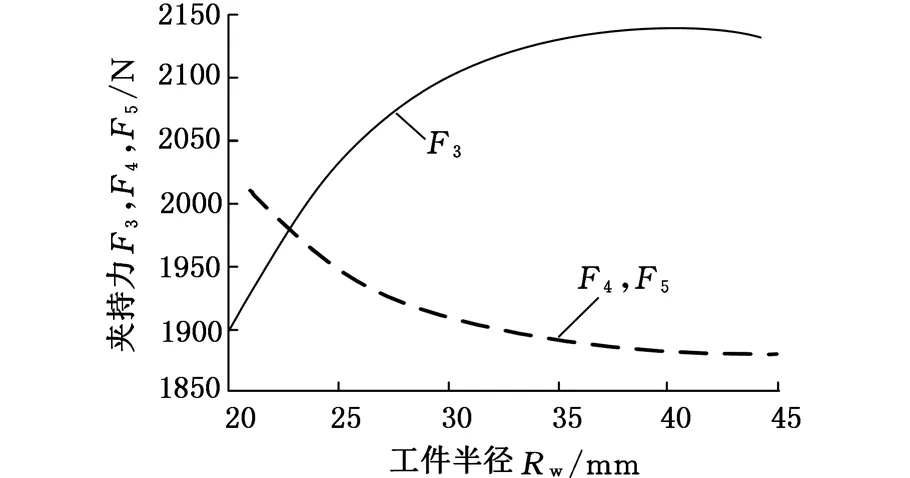
图6 三个夹持力与工件半径的关系
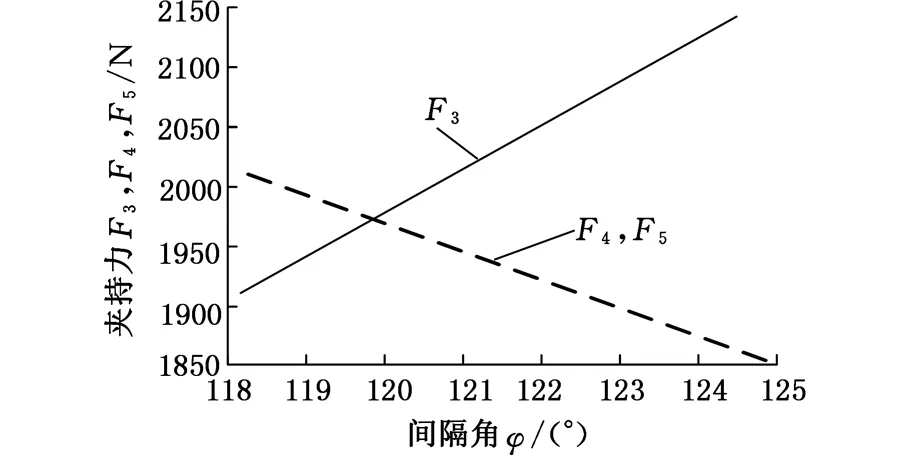
图7 三个夹持力与周向间隔角的关系
由图6、图7可见:在当前尺寸组合条件及工况下,随着被夹持工件半径的增大,三个夹持力的差值先减小后增大,即夹持质量先提高后降低。图6、图7中曲线的交点代表该中心架夹持质量最理想、最稳定的夹持情况。
4 平动凸轮廓形的优化设计
(1)设计变量。该中心架设计的夹持工件的半径R的范围为20~40 mm,预取L1=81 mm,r=5 mm,ψ=108°,θ=45°,L0、L2为独立变量,则设计变量为
x=(x1,x2)T=(L0,L2)T
(18)
(2)目标函数。为了适应夹持不同半径工件的情况,随着夹持工件半径R的变化,平动凸轮压力角α与夹持力周向间隔角φ都会变化,α的变化会使驱动力F0显著变化,φ值的变化是中心架稳定的一个重要保证,因此,将α和φ作为目标函数对于中心架的夹持质量和稳定性具有重要意义。目标函数为
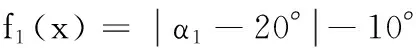
(19)
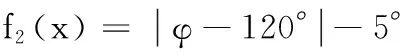
(20)
目标函数式(19)和式(20)是两个独立的函数,根据约束条件与前述的参数计算方法,采用一维搜索法可以进行求解优化。
(3)约束条件。各摆杆长度的临界值设计为
s.t.L0-L2≤0
50mm≤L0≤70mm
50mm≤L2≤70mm
(4)优化程序设计。利用MATLAB优化求解,首先在变量的可变范围内寻求目标的最优值,在最优值处检验条件是否满足,再根据最优值求出各变量的最优组合,具体方法如图8所示。

图8 优化设计流程
在给L1赋值时,为了使平动推杆的长度合理,需要对θ进行限制,其初始取值范围限定在40°~50°之间,具体取值还需考虑其他设计因素。
具体算法如下:
clc;clearall;
symsL2%将L2作为未知参变量
r=7;%夹持滚轮的半径
Rmax=45+r;%被夹持工件半径最大时,被夹持工件中心与滚轮中心的距离
L1=81; %假想的固定杆杆长的初设值L1
epsi=62*pi/180;%被夹持工件半径最大时,上夹持滚轮中心、夹持中心点连线与水平轴线之间的夹角
format long
alpha=acos((L1^2+L2^2-Rmax^2)/2/L1/L2);
%夹持不同半径工件对应的夹持角度
delta=asin(L2*sin(alpha)/Rmax);
%夹持最大工件时对应的∠O1OC角
theta=delta+epsi-pi/2;
%假想的L1杆与竖直轴线的夹角
theta=subs(theta);
L2=solve(theta-pi/4,L2);
%预设给定的θ为π/4
L2=subs(L2);
fprintf('L2=%f ',L2);
自定心中心架的设计流程如图8所示。脚本1、脚本2也可以合并为一个脚本文件(此处为了流程图的明晰,未加以合并),脚本文件2也包含有静力学、动力学分析等反映动态性能的数据输出;脚本文件3用作凸轮廓线的图形输出及点阵(点云)输出。对于流程中涉及的脚本文件代码,限于篇幅此处不作详述。
由图9可知,优化后不论是压力角还是夹持力周向间隔角度都得到了很好的控制:压力角的最小值较优化前减小了50%,压力角的最大值较优化前也减小了50%;夹持力周向间隔角度较优化前分布区间也更加集中,可以很好地满足机构对传力性能及稳定性的要求。
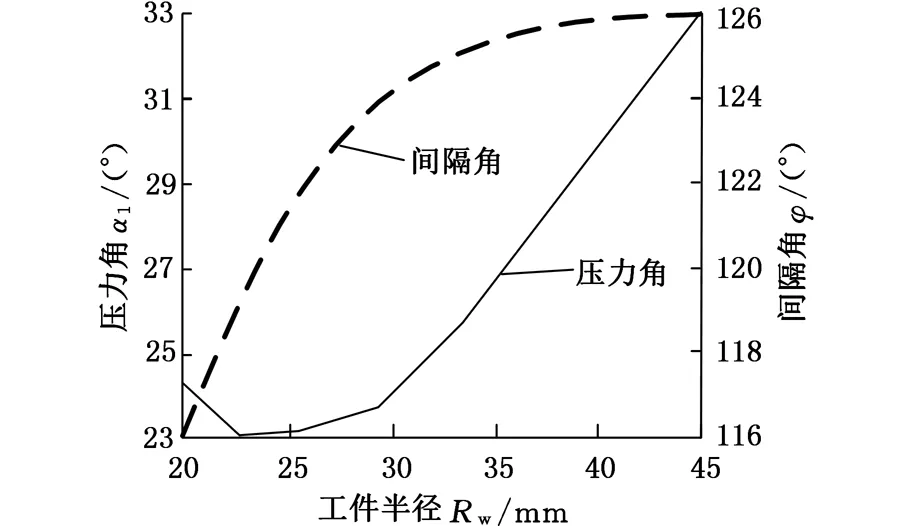
图9 优化后平动凸轮压力角、夹持力周向间隔角与工件半径的关系
5 结论
本文给出了一种磨床用自定心中心架的机构原型,建立了自定心中心架的参数组合和平动凸轮的参数化模型。对机构中的平动凸轮的两个重要参数进行优化。设计计算结果表明:
(1)平动凸轮的轮廓曲线满足了自定心中心架所要求的复杂运动规律;
(2)建立的平动凸轮廓形优化设计数学模型合理,通过优化设计使得自定心中心架的工作压力角的最小值减小了50%,压力角最大值也减小了50%,夹持力周向间隔角度的分布区间得到了改善,实现了传力性能与夹持质量的综合优化。
本研究的设计方法和思路可以为同类机构的设计提供参考。
[1]赵永强,王耀锋.自定心中心架的力学分析与仿真[J].制造业自动化,2015,37(7):99-102.Zhao Yongqiang,Wang Yaofeng. Mechanical Analysis and Simulation of Self-centering Center Rest [J]. Manufacturing Automation,2015,37(7):99-102.
[2]彭克立, 崔中, 刘运泉. 一种自动跟踪式中心架的研制[J]. 制造技术与机床, 2009(11):123-125.
Peng Keli,Cui Zhong,Liu Yunquan.Design of an Auto-tracking Central Shelves[J]. Manufacturing Technology & Machine Tool,2009(11):123-125.
[3]孙金海,杨晓磊. 自定心、滚动支撑中心架的设计[J]. 制造技术与机床,2013(8):145-146.
Sun Jinhai,Yang Xiaolei. Design of Self- centering and Rolling Supporting Steady Rest[J]. Manufacturing Technology & Machine Tool,2013(8):145-146.
[4]王伟顺,运同树. 重载机床静压刀架的设计与研究[J]. 金属加工(冷加工), 2014(14):45-46.
Wang Weishun,Yun Tongshu.The Design and Research of Heavy-duty Machine Tool Hydrostatic Carriage[J].Metal Working(Metal Cutting),2014(14):45-46.
[5] 牛福林. 手动高刚性自定心中心架[J]. 制造技术与机床,2015(10):28-29.
Niu Fuxin. Handing Good Rigidity Self-centring Centre Frame[J]. Manufacturing Technology & Machine Tool,2015(10):28-29.
[6]魏嵩.凸轮连杆自定心中心架的设计[D].新竹:清华大学,2014.
[7]Takano Y, Kimura Y, Misu A. Center Frame in Crawl-er Travel Device and Method for Manufacturing Center Frame: US,8066302[P]. 2011-11-29.
[8]Rehm F. Steady Rest:US,8226992B2[P]. 2012-09-18.
[9]Huang H C, Wei S J, Su H C. Auto-centering Appar-atus of a Steady Rest: US, 14/091066[P]. 2013-11-26.
[10]Helm P, Maurer E. Self-centering Steady Rest: US, 8726772[P]. 2014-05-20.
[11]Tsai P T H. Center Frame of CNC Machine Tool: US,14/272564[P]. 2014-05-08.
[12]Hangleiter E,Schenk P. Electric-drive Steady Rest:US, 8813616B2[P].2014-08-26.
[13]李京鲁.自定心中心架工作楔形曲线的计算[J].机械工程师,1991(11):27-28.
Li Jinglu. Calculation of Wedge-shape Curces in Self-centering Steady Rest[J]. Machinery Manufacturing Engineer, 1991(11):27-28.
[14]涂庭波. 液压自定心中心架的机构设计研究[D]. 合肥:合肥工业大学, 2008.
[15]卢学玉,谢能斌. 液压自定心中心架凸轮曲线的推导研究[J].机械设计与制造, 2008(4):24-25.
Lu Xueyu,Xie Nengbin.The Cam Curve Deduce Research of the Hydraulic Self-centred Steady Rest[J]. Machinery Design & Manufacture, 2008(4):24-25.
[16]肖凯. 自定心中心架内部进程凸轮曲线的计算[J]. 装备制造技术, 2013(3):149-150.
XiaoKai.Self-centeringCenterRackInternalProcessofCalculationoftheCamCurve[J].EquipmentManufacturingTechnology, 2013(3):149-150.
[17]WuB,YuXD,ChangXM,etal.InfluenceofWorkingParametersonDynamicPressureEffectofHeavyConstantFlowHydrostaticCenterRest[J].AppliedMechanicsandMaterials, 2013, 274: 82-86.
[18]WangWS,DongXZ,WuY,etal.OptimalDesignofHeavyLoadHydrostaticCenterRest[J].AppliedMechanicsandMaterials, 2014, 494: 611-615.
[19]石永刚. 凸轮机构设计[M].上海: 上海科学技术出版社, 1995.
[20]黄尚兵, 金光,安源,等.滚子摆动从动件盘形凸轮的设计及优化[J]. 工程设计学报,2012,19(6):449-453.
HuangShangbing,JinGuang,AnYuan,etal.DesignandOptimizationofOscillatingRollerFollowerCam[J].ChineseJournalofEngineeringDesign, 2012,19(6):449-453.
[21]WangZ,DuanR,XuX.ModelIdentificationofHydrostaticCenterFrameControlSystembasedonMATLAB[J].JournalofNetworks, 2013, 8(6): 1315-1321.
[22]李军.基于MATLAB的平面盘形凸轮机构参数化设计[J]. 煤炭技术,2011,30(3):22-24.
LiJun.ParametricDesignofPlaneDiscMechanismBasedonMATLAB[J].CoalTechnology,2011,30(3):22-24.
(编辑卢湘帆)
MechanismDesignandOptimizationofSelf-centeringSteadyRestUsedinGrindingMachine
ZhaoYongqiangWangYaofengHouHongling
ShaanxiSci-TechUniversity,Hanzhong,Shaanxi,723001
Aprototypeofself-centeringsteadyrestforgrindingmachinewasdesigned;theparametercombinationsofsteadyrestandparametricmodeloftranslationalcamwereestablished.Optimizationdesigngoalandoptimizationfunctionwerepresentedbycombiningscreeningofdesignparameters.TheoptimizationcalculationprograminMATLABwasaccomplished.Twoparametersofthetranslationalcamwereoptimizedbasedonguaranteeingtransmissionperformance,clampingstabilityandespeciallyclampingaccuracy.So,acompletesolutionforhighaccuracy-centeringsteadyrestdesignwasprovided.
self-centeringsteadyrest;slenderaxisgrinding;translationalcam;parameteriza-tiondesign
2015-10-19
陕西省科技统筹创新工程重点实验室项目(2014SZS16-K03);陕西省教育厅专项科研计划资助项目(16JK1166);陕西理工大学研究生创新基金资助项目(SLGYCX1610)
TH161
10.3969/j.issn.1004-132X.2016.17.009
赵永强,男, 1976年生。陕西理工大学机械工程学院副教授。主要研究方向为先进成形工艺与精密加工技术设备及控制、电动汽车及节能技术。发表论文40余篇。王耀锋,男,1988年生。陕西理工大学机械工程学院硕士研究生。侯红玲,女,1976年生。陕西理工大学机械工程学院副教授。
