振动对TBM液压泵泵轴受力及疲劳寿命影响分析

杨忠炯，董　栋

(1.高性能复杂制造国家重点实验室,湖南 长沙 410083; 2.中南大学 机电工程学院，湖南 长沙 410083)



振动对TBM液压泵泵轴受力及疲劳寿命影响分析

杨忠炯1，2，董栋2

(1.高性能复杂制造国家重点实验室,湖南 长沙 410083; 2.中南大学 机电工程学院，湖南 长沙 410083)

针对硬岩掘进机(tunnel boring machine,TBM)强振动工况，分析引起泵轴疲劳失效的两种机理：载荷与材料性能变化.建立了泵轴在强振动下的受力仿真模型，仿真得到泵轴稳态受力幅值随频率及振幅均呈线性增加.根据经验数据，获得不同工况下的S-N曲线修正模型.建立泵轴的有限元模型，加载不同工况的载荷与材料参数，得到振动参数影响泵轴疲劳寿命的规律.结果表明：当振幅小于3 mm，频率小于20 Hz时，泵轴总能满足对寿命要求;当振幅大于4.8 mm时，不能满足其寿命要求;当频率为10 Hz时，能满足泵轴疲劳寿命的最大振幅为4.3 mm.

硬岩掘进机；振动；叶片泵泵轴；疲劳寿命

0　引言

硬岩掘进机(tunnel boring machine, TBM)是用于开挖硬岩地质隧道的大型施工设备，工作在大功率、强振动的环境下.MB264-311型TBM的撑靴液压系统有3台不同的液压泵，其中包括一台双作用叶片泵，其工作转速1 000 r/min，排量40 mL/r，额定工作压力6.3 MPa，工程要求其工作寿命在8 000～10 000 h.该叶片泵作为快速收缩及快速伸出回路的辅助泵源，在工作过程中常发生泵轴断裂问题，不能满足工程要求[1-2].文献[3-4]分析了交变载荷下结构的静应力疲劳失效.文献[4]提出了轴承的振动模型.文献[5-6]分析了振动频率对结构疲劳寿命的影响.

目前，对振动环境下泵轴的疲劳寿命的研究很少，因此本研究运用ANSYS/APDL参数化建模，研究了振动环境对泵轴疲劳寿命影响.

1　泵轴疲劳寿命分析原理

图1所示为某型叶片泵的装配结构图，泵轴左端与中部由两个不同型号的轴承支承，轴的左端第二段通过花键与叶片转子连接，泵右端通过联轴器与驱动电机相连.

TBM振动频率在5～20 Hz，振幅在0～6 mm.根据TBM某项目实测驱动电机轴附近的振动时域波形可知，振动频率为10.24 Hz，振动加速度为3.53 m/s2.

1.1振动引起载荷变化

根据泵的装配关系，将轴承简化为一个弹簧-质量模型，分析泵轴在径向基础振动下的受力情况，则该系统为两自由度基础振动模型，原轴受力模型如图2所示.

根据牛顿第二定律，建立泵轴的受力数学模型如下，垂直方向受力平衡：

(1)

式中：m为泵轴质量；x1为泵轴位移；x2为基础振动位移，x2=Asinωt；k1为左端轴承径向刚度；k2为右端轴承径向刚度；θ为泵轴绕质心转动角度；L1为质心距泵轴左轴承距离；L2为泵轴距泵轴右轴承距离.而力矩平衡方程为

k2(x1-x2+L2θ)L2=0.

(2)

式中：Jc为泵轴质心转动惯量.

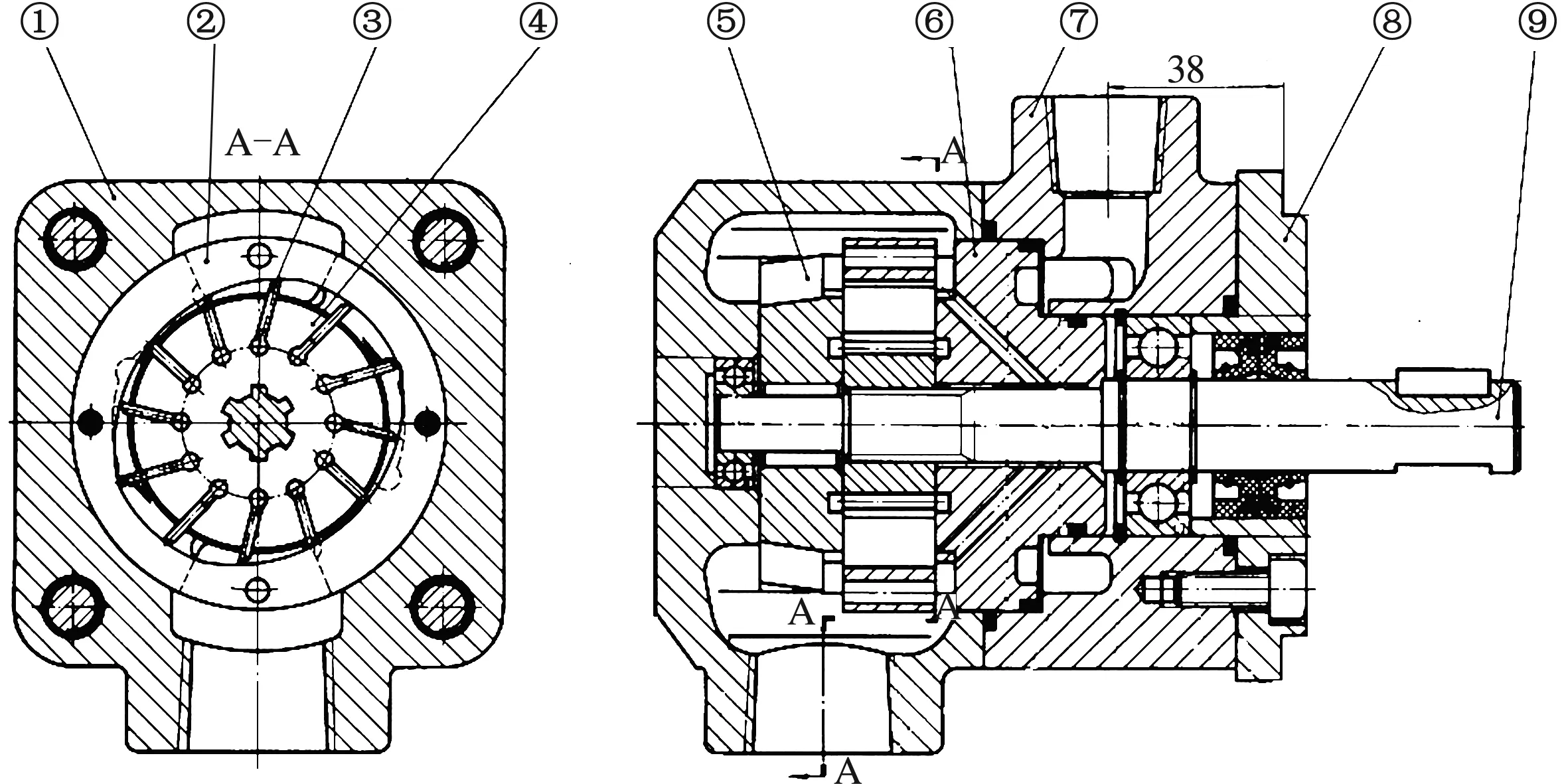
1—左泵体；2—定子；3—叶片；4—转子；5—左配流盘；6—右配流盘；7—右泵体；8—盖板；9—泵轴.图1　叶片泵装配图Fig.1　Assembly drawing of vane pump

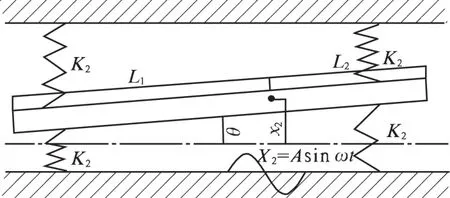
图2　泵轴受力模型Fig.2　Force model of pump shaft

轴承刚度方程为

(3)

式中：m1为轴承座及部分轴承另件的质量和；m2为短轴与另一部分轴承零件的质量和；ωR为共振

频率；K为轴承的径向刚度.

根据以上公式，运用Matlab/Simulink建立泵轴的受力仿真模型，如图3所示.对振动信号输入采用微分环节，对泵轴位移输出计算采用积分环节，仿真计算结构参数为左轴承径向刚度为2.235×106kg/cm，右轴承径向刚度为2.125×106kg/cm，质心转动惯量为47.9 g/mm2，质心到左轴承距离为98.71 mm，质心到右轴承距离为95.29 mm，泵轴质量为3.75 kg.模型以固定步长ode3(bogacki-shampine)求解器求解，仿真步长设定为0.001 s.仿真振动频率为1、10、20 Hz时不同振幅下的泵轴受力情况.

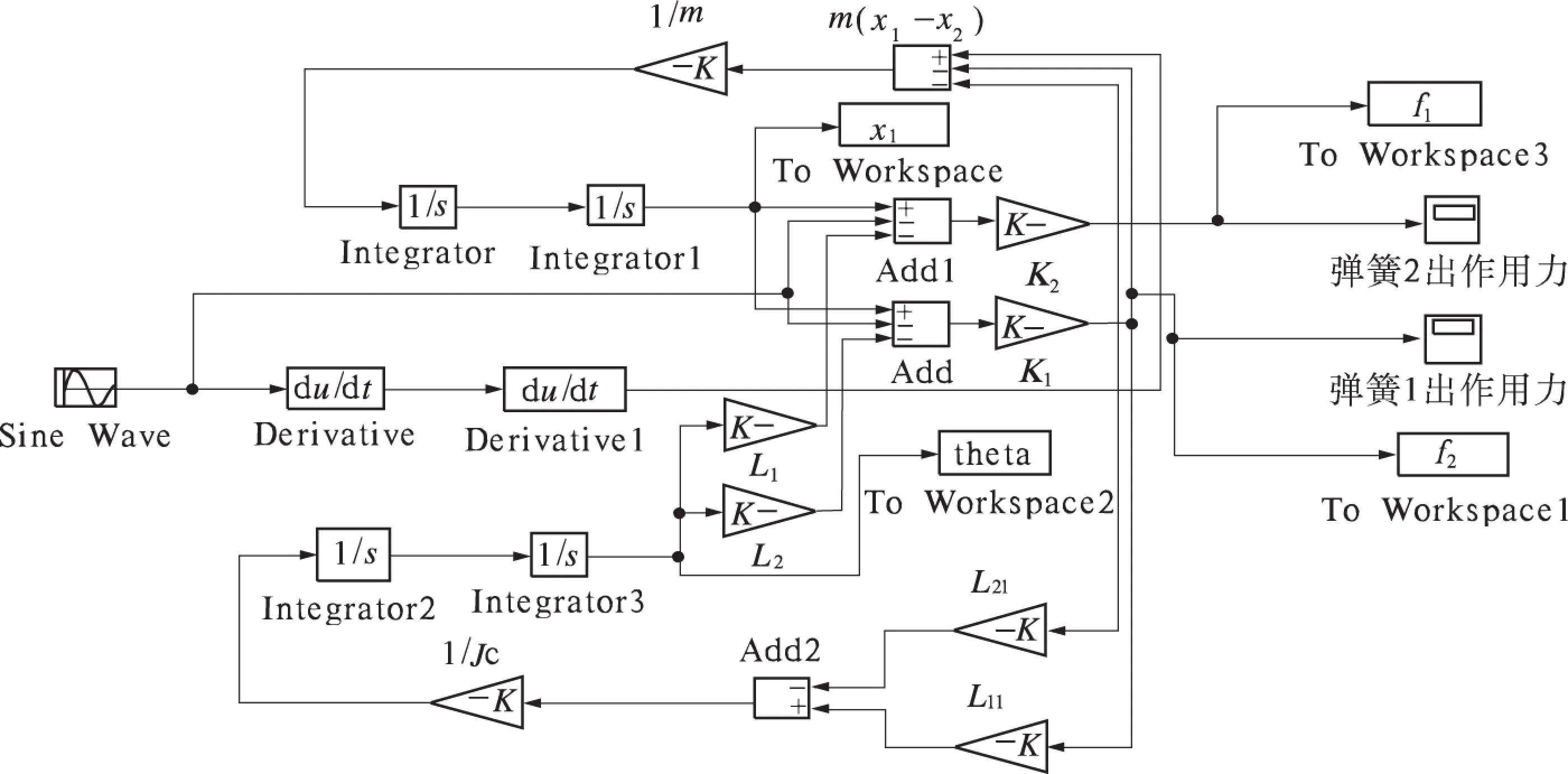
图3　振动下泵轴受力仿真模型Fig.3　Simulation of force on shaft under vibration

如图4～6所示，泵轴的受力在达到稳定后呈现正弦波动.1 Hz时稳态受力的幅值接近零，10 Hz时受力幅值达到223.5 N;20 Hz受力幅值达到912.5 N.比较不同频率图中受力幅值发现，随频率增加，泵轴受力幅值有显著增加.分析受力幅值随频率增加的变化趋势，发现其相关系数趋近于1，即受力随频率线性增加.10 Hz时，振动幅值为1、2、3、4、5 mm时所对应的泵轴受力幅值分别为44.7、89.4、134.1、178.8、223.5 N.分析表明，泵轴受力峰值随振幅同样是线性增加.

1.2振动引起材料性能变化

根据前人研究，振动对材料性能的影响主要由振动频率引起.文献[5]指出，加载频率对金属材料的疲劳寿命曲线有很大影响.文献[6]通过试验获得10 Hz下用Basquin方程式描述S-N的参数值.方程式为

(4)

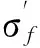
图4　1 Hz时不同振幅下的泵轴受力图Fig.4　Force on shaft under different amplitude by 1 Hz

图5　10 Hz时不同振幅下泵轴的受力图Fig.5　Force on shaft under different amplitude by 10 Hz

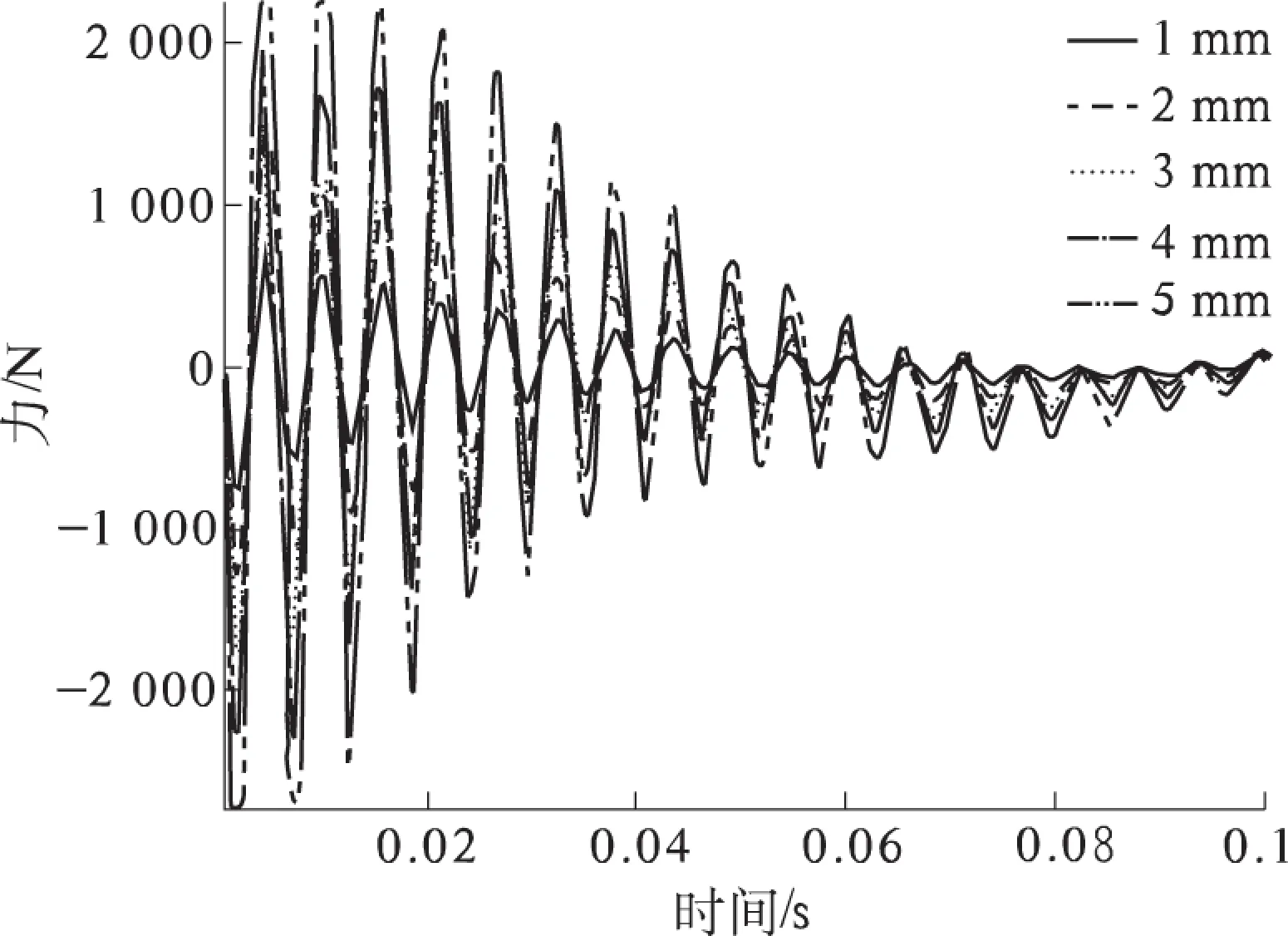
图6　20 Hz时不同振幅下的泵轴受力图Fig.6　Force on shaft under different amplitude by 20 Hz

2　泵轴模型建立及疲劳分析

2.1泵轴有限元建模

根据泵轴的结构参数，运用ANSYS/APDL语言参数化建立有限元模型.材料杨氏模量为2.11E11 Pa，泊松比为0.277，质量密度为7.87 g/cm3.许用应力 [σ]=171.57 MPa，由于模型受扭转剪力，选择单元类型为Solid185，自由划分为22 996个节点，118 261个单元.图7为Y方向位移与总位移图，图8为等效应力图及危险部位图.根据泵轴的安装及受力情况，加载固定约束于轴端，分别在两轴承处加载振动下泵轴受力，由于ANSYS/Fatigue模块的局限性，加载受力按受力幅值静态加载,且加载扭矩在花键部位.再由等效应力从图8(b)可以看出，最大等效应力即泵轴的危险部位是花键根部.

2.2泵轴疲劳计算分析

(1)疲劳参数.根据泵轴的结构参数，选择钢材的敏性系数q为0.5，结构的理论应力集中系数α为1.32，根据理论应力集中系数与有效应力集中系数的关系式[7]：

k-1=q(α-1).

(5)

图7　Y方向位移与总位移图Fig.7　Y direction and total displacement

图8　等效应力图及危险部位图Fig.8　Vonmise and dangerous position

计算得有效应力集中系数为1.16.根据钢材截面形状系数图，由于轴为实心轴，所以尺寸效应选择为1，泵轴表面粗糙度为1.6，通过精车加工后，其扭转剪切疲劳表面质量系数选择为0.9.

(2)疲劳计算结果.通过对静力分析下危险位置计算，考虑结构的对称性，选择疲劳设置为1 LOCATION、1 EVENT、2 LOADS进行疲劳计算分析，其中2 LOADS分别为泵受力最大值与最小值.1 LOCATION为花键的根部位置.疲劳应力s如表1所示.

表1　疲劳计算存储结果Tab.1　Result of fatigue calculation　MPa

ANSYS疲劳计算模块采用简化的弹塑性假设和Miner疲劳累积求和法则，认为使用应力下的循环次数与该应力下材料的疲劳寿命比值等于1，即达到疲劳破坏.根据寿命要求，实际循环次数为0.6E8.

(3)振动参数对疲劳寿命影响.分别运用不同振幅与频率下的泵轴受力进行加载，求得对应的许用疲劳循环次数如图9所示.

图10为循环次数俯视图，图中左下部深色与浅色形成的交叉线以下表示许用循环次数小于要求循环次数.从俯视图可以看出，随着振幅与频率增加，许用循环次数线性减小.当振幅在3 mm以下时，频率在20 Hz以下都能满足寿命要求;当振幅大于4.8 mm时，均不能满足寿命要求;当振幅在3 mm与4.8 mm之间，由图10中深色与浅色交界曲线可以看出，随振幅增加，许用循环次数在近似线性减小，即疲劳寿命线性减小;当频率为10 Hz时，满足寿命要求的最大振幅为4.3 mm.

图9　不同振幅与频率下的循环次数图Fig.9　Allowance cycles under different amplitudes and frequencies

图10　循环次数俯视图Fig.10　Top view of the allowance cycle number

3　结论

(1)建立泵轴在振动下的受力仿真模型.仿真表明，振动下的瞬态受力远大于稳态受力.同时，随振幅与频率的增加，稳态受力均按线性规律增加.

(2)建立泵轴有限元模型，花键为危险部位.当振幅小于3 mm，频率小于20 Hz时，泵轴能满足寿命要求;当振幅大于4.8 mm时，不能满足其寿命要求;当振幅在3～4.8 mm之间时，随着振幅与频率增加，许用循环次数即疲劳寿命线性减小；当频率为10 Hz时，能满足泵轴疲劳寿命的最大振幅为4.3 mm.

[1]杨忠炯, 李洪宾, 周立强, 等. 强冲击下先导式溢流阀先导阀芯自激振动仿真[J]. 华中科技大学学报(自然科学版), 2015,43(4):58-63.

[2]刘竹丽, 赵敏敏, 马朋朋, 等. 基于ANSYS的斜齿轮副接触分析与可靠性分析[J]. 郑州大学学报(工学版), 2015,36(2):6-9.

[3]OST W, DE B P, VAN W J. Failure investigation and redesign of piston and pump shafts[J]. Engineering failure analysis, 2009,16(4):1174-1187.

[4]杨大鹏, 张雪艳, 赵辉, 等. 疲劳载荷循环比与频率对裂纹扩展速率的影响[J]. 武汉大学学报(工学版), 2013,46(1):133-136.

[5]刘东星, 薛红前, 邵闯, 等. 不同载荷频率条件下300M钢疲劳性能研究[J]. 机械科学与技术, 2011,30(11):1951-1954.

[6]罗德扬, 宋学曾. 正弦激振测定轴承的刚度和阻尼[J]. 振动测试与诊断, 1983，23(2):21-28.

[7]李舜酩. 机械疲劳与可靠性设计[M]. 北京：科学出版社, 2006:102-122.

The Influence of Vibration on the Force and Fatigue Life of Shaft of TBM Vane Pump

YANG Zhongjiong, DONG Dong

(College of Mechanical and Electrical Engineering， Central South University， Changsha 410083， China)

In view of the fact that TBM works under vibration environment, this paper has analyzed two reasons of fatigue of the pump shaft under vibration: the change of loads and the material performance. We build the model of the vane pump by MATLAB/SIMULINK is built. The results of simulation show that the stable force on pump shaft has active linescaple relationship with the frequency and amplitude. According to the empirical data, the S-N curve in different situation was obtained. And the finite element model of the shaft was established. Adding different loads and the material parameters on the model, the influence rules by vibration are obtained. The results indicate that: when the amplitude is below 3 mm and the frequency is below 20 Hz, it can always satisfy the request of fatigue life. It cannot satisfy the request of fatigue life when the amplitude is above 4.8 mm. When the frequency is 10 Hz, the maximum amplitude to satisfy the fatigue life of shaft is 4.3 mm.

TBM; vibration; vane pump; shaft; fatigue

2015-09-08；

2015-11-10

国家重点基础研究发展计划资助项目(2013CB035404)

杨忠炯(1963—)，男，湖南长沙人，中南大学教授，博士，主要从事流体动力学研究，E-mail：yzj7072@126.com.

1671-6833(2016)04-0006-05

TH312

A

10.13705/j.issn.1671-6833.2016.04.002