罗素的替代理论

郑伟平

厦门大学哲学系

zhengweiping@xmu.edu.cn



罗素的替代理论

郑伟平

厦门大学哲学系

zhengweiping@xmu.edu.cn

在1903年到1908年间，罗素提出、发展并最终放弃了一种悖论解答方案——替代理论。罗素从摹状词理论中得到启示：悖论源自虚假抽象。替代理论的基本概念“替代”可以避免虚假抽象，通过使用替代运算来定义类和自然数，替代理论在一定程度上获得了成功。然而替代悖论的发现促使罗素最终放弃了替代理论，并走向了分支类型论。

罗素悖论；替代理论；类型论

在1901年罗素悖论被发现以后的十年时间里，罗素一直致力于解决罗素悖论，以实现其逻辑主义理想。在1903年出版的《数学原则》一书中，罗素提出了解决罗素悖论的最初方案——简单类型论。在1910年出版的《数学原理》一书中，罗素又提出了著名的分支类型论。鲜有人知的是，在1903到1910年间，罗素还提出了一个替代理论。与类型论强调变元有类型区分不同，替代理论中变元是没有类型区分的。罗素这一思想进程（“简单类型论—替代理论—分支类型论”）遵循了“正反合”的规律，体现了罗素在解决悖论问题时思想的一波三折。是什么原因促使罗素最终放弃替代理论而发展出分支类型论？替代理论与罗素同时期的摹状词理论有何关系？这些都是罗素研究和逻辑史研究的重要主题。

罗素采用和放弃替代理论的关键都是逻辑悖论的存在。本文致力于提供一副罗素替代理论的基本图景1在罗素研究领域，国外学者已经对此主题进行了一些研究。但是国外学者，例如兰蒂尼，在讨论罗素替代理论的时候缺乏足够的罗素文本支持，导致不易区分研究者观点与罗素观点，且理论出发点不同导致他们的叙述方式对于接受标准逻辑教科书训练的国内读者是不容易掌握的。具体可以参见［3］。，拟分为三部分：第一部分介绍罗素替代理论的背景——命题悖论的产生导致罗素放弃简单类型论；第二部分描述替代理论的基本理念和核心概念，以及罗素对类和自然数的定义，力图阐明替代理论能够回避导致悖论产生的虚假抽象；第三部分根据罗素手稿和现代逻辑的标准记法给出替代悖论的形式证明，并指出替代悖论的出现是导致罗素最终放弃替代理论的根本原因。

1　命题悖论与虚假抽象

罗素认为一个令人满意的悖论解决方案必须满足以下三个条件：“第一是绝对必要的，那就是这些矛盾必须消失。第二个条件最好具备，虽然在逻辑上不是必需的，那就是，这个解决应该尽可能使数学原封不动。第三个条件不容易说得正确，那就是，这个解决仔细想来应该契合一种东西，我们姑且称之为‘逻辑的常识’，那就是说它最终应该是我们一直期待的。”（［5］，第70页）简单类型论之所以不是一个令人满意的悖论解答方案，就在于它无法满足第一个条件——解决悖论。

在《数学原则》附录B中，罗素提出了一个简单类型论所无法解答的悖论——“命题悖论”（［4］，第527页）。对于每一个实体x，我们可以合法地得到一个命题x=x，也就是说我们可以在实体和命题之间建立一种一一对应关系，由此我们可以说命题的数目和实体的数目一样多。但是在《数学原则》中，罗素把命题看作是一种单独的类型，我们可以把所有的命题收集起来构成一个类。根据康托尔的观点，集合幂集的基数要大于该集合的基数，即一个集合中元素的数目要小于该集合子集的数目。由于在《数学原则》中类是实体，所以命题幂集的数目总是等于命题类的数目，这就违反了康托尔定理。

这个“命题悖论”可以表述如下：

假设M是一个命题类，那么命题“M中的每一个m是真的”或者是M的一个元素，或者不是M的一个元素。

考察一个类W，W由这样一些命题组成，这些命题断定了某个特定的命题类中所有命题的真，但这些命题自身又不是该命题类的元素。W的形式化表述如下：

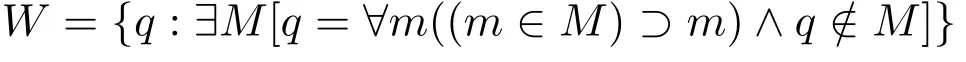
在这个式子中，值得注意的是，“M 中所有的命题皆为真”就是用∀m((m∈M)⊃m)来表述的。

(1)考察命题p，p断定了W中所有的命题都是真的，即p=∀r((r∈W)⊃r)，我们可以问p是W中的一个元素吗？

(2)如果p是W中的一个元素，那么根据W的定义，p不是W中的一个元素。

(3)如果p不是W中的一个元素，那么p满足了W的定义，p是W中的一个元素。矛盾！

1906年，罗素发表文章《论超穷数理论和有序类型理论的某些困难》（［7］）。在文中，罗素抛弃了简单类型论，并给出了他为解决悖论所提供的三个方案：1、曲折理论（Zigzag Theory，也称为“之字形理论”）2罗素在1906年三月十五日给尤尔丹的信中给出了“曲折理论”这个提法，但是唯一讨论到这个理论的已出版文献就是1906年的《论超穷数理论和有序类型理论的某些困难》这篇文章。；2、限制大小理论（The Theory of Limitation of Size）；3、无类理论（The No-Class Theory）。正如哥德尔指出的，“罗素自己后来关于解决悖论的工作，并没有按照自己指出的第一和第二个方向去做，而在很大程度上是建立在更激进的想法，即‘无类理论’之上的。”（［1］，第453页）罗素之所以选择无类理论，一个简单的思路是：类引发了悖论（例如“那个由不包含自身的类所组成的类”就是罗素悖论根源），那么只要我们不再把类当作对象，而是当作某种逻辑构造，就可以排除此类悖论。但是由于无类理论也未能逃脱悖论的困扰，罗素不得不重新反思悖论的起源问题，并放弃了悖论源自“虚假抽象”的最初观点。在彭加莱提出了悖论来自于“自我指称”（self-reference）这个观点之后，罗素开始承认类型区分的必要性，并最终走向了分支类型论。

罗素在1906年3月给尤尔丹（Jourdain）的一封信中写道：

在1904年六月左右，我努力要来构造一个与现有理论类似的替代理论。但我由于缺少指谓理论而失败了，另外我也未能区分开用一个常项去替代一个常项，以及用一个常项来对一个变元进行赋值……在去年秋天，作为一个新指谓理论的影响，我最终发现替代依然是有效的，并且所有一切都变得豁然开朗起来。（［2］，第79页）

从1903年到1906年，罗素都在认真考虑如何在没有变元限制的情况下构造出一种可用以推出数学的逻辑，同时这种逻辑又能避免罗素悖论。在《数学原则》出版之后，罗素开始认真研究其逻辑主义的共同战友弗雷格的著作。从罗素在1903到1904年期间写作的手稿的命名3这些手稿包括《函数与对象》、《论意义与指谓》、《论语词的意义与指谓》，它们都被编入来看，罗素很重视弗雷格的工作。这一时期甚至可以称为是罗素的“弗雷格主义时期”。这一时期罗素的工作重点是希望从弗雷格的逻辑主义中寻找到一些解决罗素悖论的启示。

虽然罗素反对弗雷格在《函数与对象》一文所持有的观点，即函数是不完全的，但是罗素同样受到了这种不完全的函数观念的重要影响，其直接结果就是罗素提出了“不完全符号”（Incomplete Symbol）概念。而1905年的《论指称》一文4关于1905年的《论指谓》一文，有两点评论：第一、国内的研究大多只是就文谈文，没有把《论指谓》放在罗素悖论研究和逻辑主义规划的大背景下来理解，导致了《论指谓》的出现成为一个很突兀的事情；第二、《论指谓》一文的脚注表明该文的主题延续了《数学原则》一书中的相关主题的研究，因此该文是罗素逻辑主义研究的一个发展阶段。对此主题的讨论详见［11］。也正是这种思路影响下的产物。

在“四的平方根是偶数”这个命题中，主项是“四的平方根”，但是这个命题实际上是关于2的一个命题。根据弗雷格的观点，“四的平方根”起到了专名的作用，它的意谓是2。罗素反对这种观点，罗素的研究成果是“四的平方根”表达了比2的专名“2”更多的东西，或者说它并不是一个专名。罗素进一步的结论是“四的平方根”是一个不完全符号。不完全符号的出现给了罗素解决悖论的全新思路：除了摹状词，类、关系和函数也被看作是不完全符号。罗素从摹状词理论中学到的教训是：

在任何句子中，一个单一的语词，或者一个单一的短语，当它从语境中被分离出来时，它往往就失去了意义。在这种情况下，如果一个语词或短语被错误地当作拥有一个独立意义，我们称之为“虚假抽象”（False Abstraction），悖论和矛盾就是这么来的。（［7］，第165页）

我所提倡的理论是类、关系、数，以及数学处理的几乎所有东西，都是虚假抽象。（［7］，第166页）

罗素的这一段论述应加以足够的重视，因为它实际上给出了替代理论的哲学依据，也给出了悖论形成的原因。这段论述的观点总结如下：

(1)离开语境的语词或短语是没有意义的；

罗素的这种观点和弗雷格的语境原则如出一辙，这也是分析哲学的重要方法论。语境原则中的“语境”一般指的是命题，或者句子。罗素的这种观点其实是对其1900年把命题分析作为哲学研究起点的观点的进一步发展，随着罗素逻辑思想的成熟，以命题为核心的思考方式也愈发完善。

《罗素全集》第四卷，详见［9］。

为什么罗素会认为单独出现的语词没有意义呢？因为罗素通过考察摹状词得出结论：日常专名并不是一个实体的名字，与此同时一个语词的意义就是该语词的指称。在《论指称》一文中，罗素还得出了重要结论——“这就是我想提倡的指称理论的原则：指称词组本身绝不具有任何意义，但在语词表达式中出现指称词组的每个命题都有意义”（［6］，第480页）。因此在罗素看来，语词只有在命题语境下加以考察才是有意义的，否则是无意义的。

(2)一个语词或短语如果被错误地当作拥有一个独立意义，则将导致“虚假抽象”；

一个语词或短语被当作拥有一个独立意义即表明该语词或短语的指称是对象，或实体。对于这一观点，罗素在《论指称》中已经给予了激烈的批评，因为这种观点会引起空专名问题，或者空摹状词问题，甚至是悖论问题。按照罗素的观点，语词或短语是没有指称的，罗素的依据是：任何不完全符号都是没有独立意义的。这种立场在日常语言下很难被察觉，例如，人们很难看出，为什么“柏拉图的老师”这个摹状词没有意义，而不指向某个被称作“苏格拉底”的实体？对此，罗素在《论指称》中为我们提供了答案：日常命题在翻译为逻辑命题之后，原先日常命题中的摹状词都消失了。

(3)矛盾和悖论的来源是虚假抽象；

罗素清晰地表述了矛盾和悖论的来源就在于我们把一个短语或语词当作拥有独立意义，即拥有某个指称。而这显然不同于罗素1908年所承认的“自我指称”是悖论的起因的观点。在罗素看来，悖论和矛盾之所以会出现，就在于我们单独地考察了某些会引发悖论的类或函数。如果我们认识到它们只是“虚假抽象”，认识到它们出现在其中的句子的真实意义，那么便能避免悖论的出现，进而实现逻辑主义目标。如果假设一个短语或语词都拥有一个独立意义，即都有一个实体作为其指称，那么该语词所指示的实体便可以作为变元的值出现在某些命题函数之中。当我们使用“那个由所有不属于自身的类所组成的类”这个短语时，按照虚假抽象的观点，人们认为它有一个实体作为其意义。

(4)类、关系、数以及数学处理的几乎所有东西，都是虚假抽象。

罗素认为一个完善的悖论解答方案应该满足三个条件：1、悖论必须消失；2、数学原样不动；3、符合逻辑常识。（［5］，第70页）而观点(4)表明了数学在实质上是构造出来的，更具体地说是逻辑构造出来的，因为类、关系、函数和数等这些数学处理的对象在罗素看来都是逻辑可构造的。例如在罗素的替代理论中，类被看作是一种不完全符号p/a，它是没有单独意义的，它只有作为一个整体的一部分才获得了意义。这种构造数学的想法遭致了很多人的批评，因为它改变了数学的涵义。例如几何学的直观意义看上去就被改变了。哥德尔批评道，“为了实施这个方案，人们势必预设算术，而这种算术不过证明了甚至这种有限的逻辑都不能建立在无物之上。”（［1］，第457页）

从以上论述和引文中，我们很清楚地看到了罗素的思想进程：发现命题悖论——放弃简单类型论——发展指谓理论——创立不完全符号理论——寻找替代理论。

2　替代理论的基本理念

在替代理论中，罗素首先区分了两个重要的概念：对应于命题函数的指派（Determination）和对应于替代理论的替代（Substitution）。前者把一个常项指派为一个变元的值，后者用一个常项去替代另一个常项或变元。罗素认为这两者适用于不同的问题。指派适用于回答“当x=3时，x2+x+2的值是什么”或者“假设x=苏格拉底，我们能从‘如果x是人，那么x是有死的’得到什么样的命题”（［7］，第167页）这类问题，显然指派指的是对命题函数中的变元进行赋值。而替代则适合于回答“柏拉图是一个哲学家，并且苏格拉底也是一样的”（［7］，第167页）这样的问题。当罗素说“苏格拉底也是一样的”时，意思是苏格拉底是一个哲学家。这是用“苏格拉底”去替换命题“柏拉图是一个哲学家”中的“柏拉图”得到的新命题。可见替代通常是指在一个命题中用一个常项去替代另一个常项，但它同样适于用常项去替代一个命题函数中的变元。罗素认为指派与替代之间的区分在面对命题函数的时候不是很清楚。例如，对于“x是一个哲学家”，在对x指派苏格拉底或x指派柏拉图时都是真的；并且用苏格拉底或柏拉图替换x后得到的新命题也都是真的。正如罗素所说“指派和替代一般都会导致相同的结果，并且出于这个理由作为一个规则，它们之间的区分并不是很清楚的。”（［7］，第167）

在罗素看来，赋值与替代之间的差别可以通过下述情况表现出来。

考察函数x=a，它是一个x的函数，而且它只对指派a为真，也就是说如果我们把a赋予到x之上，所得到的结果是一个其值为真的命题a=a。但如果我们考虑这个命题函数的值a=a并且用b替代a，我们得到了b=b，而它并不是那个命题函数的值。因此虽然a=a是命题函数x=a的值，然而通过在a=a替代a并不能得到该函数的其他值。（［7］，第168页）

罗素认为我们可以看出指派和替代的重要差别：当变元在函数中有多次不同的出现，替代运算可以统一地处理这些变元，而指派则被限制在变元的某些出现中。在面对多元命题函数时，指派与替代之间的区别更加明显。对于命题函数ϕ(x，x)，指派有多种结果。如果我们只对该命题函数中的变元x的一次出现进行指派，那么所得到的结果仍然是一个命题函数，只不过它从二元命题函数变成了一个一元命题函数。在替代下只有一种结果，那就是用一个常项去替代该命题函数中变元x的全部出现，得到的总是一个命题。

至此我们可以看到替代与指派是不同的。由于罗素已经把命题函数视作一种虚假抽象，罗素在放弃命题函数概念的同时也放弃了指派概念，并采用了与替代概念相对应的替代运算。

替代理论中最基本的概念就是“替代运算”，即p/a；b！q5罗素对替代运算的记法并不统一，有时替代运算也被记为p(b/a)！q或者pab！q，它们都表示“用a去替代p中的b得到了q”，详见［7］，第168页。但是对罗素来说，这些不同的记法表现了替代运算不同的特性。，读作“在p中用b替代a在p中所有的出现而得到q。”（［7］，第168页）替代运算可以被看作是罗素替代理论中的逻辑常项，是不可定义的。如果p是“苏格拉底是人”，a是“苏格拉底”，而b是“柏拉图”，p/a；b！q便是“用柏拉图替代‘苏格拉底是人’中的苏格拉底而得到‘柏拉图是人’”（［7］，第168页）。替代理论的一个基本原则是：在一个替代运算中出现的“p”、“q”、“a”、“b”并不是像“当今法国国王”一样的摹状词，而应该是真正实体的名字（［7］，第168页）。替代运算也被看作适用于所有实体。

基于替代概念，罗素定义了替代理论的一些基本概念。

p/a；x！q中的q我们可以记作p/a；x，因此可以得到：

p/a；x.=.用x替代p中的a所得到的产物。（［7］，第169页）

如果a并不出现在p，那么替代运算p/a；b！q也是有一个值的。罗素认为如果a不出现在p中，那么用任何实体替换p中的a产生的结果都是p自身。罗素把这种情况定义为：

a在p之外 .=：(x).p/a；x！p。（［7］，第169页）

它读作：a在p之外，当且仅当对于x的所有值而言，用x去替换p中的a产生的结果仍然是p。

相应地，“a在p中”可以定义为：

a在p中 .=.～｛a在p之外｝。（［7］，第169页）

在替代理论中，否定被看作是一个命题联结词，或者说是命题算子，因为否定运用于其上的实体是有真假的。6罗素的否定定义恰恰表明罗素在1906年还没有清晰的句法语义区分，一个命题的否定表明该命题是假的。按照罗素的这种思路，～～q.=.～(q是假的)，那么在替代理论中p单独出现时即表明p是真的。罗素很快意识到这种观点是很难令人信服的，在随后的手稿中，罗素采用了新的否定定义：～a=df(x)(a⊃x)。这个新定义继承了《数学原则》中的否定定义。因此《数学原则》中的连接词并不如同兰蒂尼和格里芬所认为的那样是一种项联结词，详见［10］。当罗素使用一个字母p来表示一个命题时，该命题是真的，与此同时，罗素认为一个命题的否定是：

～q.=.q是假的。（［7］，第169页）

因此“a在p中”表明“a在p之外是假的”。

另外对于两个实体p和q，除了“…在…之中”，还有另一种关系：p独立于q表明p和q没有共同的组成部分。罗素将其定义为：

p独立于q.=.(x).～(x在p中.x在q中)。7罗素在这个定义中用“.”来表示括号，“x在p中.x在q中”等同于“(x在p中)(x在q 中)”，它表现了一个逻辑合取。这种表现方式跟《数学原则》中的表现方式是相同的。（［7］，第169页）

罗素将实体间的同一关系理解为如果用y去替换x中的x，得到的结果是x，同一关系被罗素定义为：

x=y.=.x(y/x)！x。（［7］，第169页）

这一定义表明罗素对同一和等价不做区分。那么替代理论中的“…在…之中”和“…独立于…”是否也是项联结词？答案是肯定的，替代理论中的联结词都是项联结词8经典逻辑中并没有项联结词这一提法，但是在替代理论中，罗素把同一就看作是一种实体之间关系，=也被看作是一种项联结词，不过否定、蕴涵等联结词仍然是命题联结词。格里芬和兰蒂尼等人的解读是错误的，详见［10］。，因为在替代理论中的符号“a”、“b”、“q”、“p”等都是实体符号。

在p(x/a)中，罗素称x/a为一个“一元替代”，当然我们也可以得到“二元替代”(x，y)/(a，b)，依照这种方法，还可以得到多元替代。类似地，在p/a；x中，罗素称p/a为一个方程式（Matrix）。罗素认为“替代或方程式都不是实体，而仅仅是一个类似于d/dx的运算；也就是说，符号x/a和p/a自身都是完全没有意义的，并且只有作为合法命题的一部分才是有意义的。”（［7］，第167页）基于这一观点，罗素认为：

我所要提倡的理论是，这个模糊的符号p/a代表了一个类。类似的，p/(a，b)代表一个二元关系，p/(a，b，c)代表一个三元关系，诸如此类。它们之中没有一个是实体，并且因此不存在诸如类或关系这样的实体。（［7］，第170页）

在替代理论中，类或关系不是实体，因而也避免了虚假抽象。类表达式“p/a”表示的是“用…去替代p中的a得到的结果”，“用…去替代p中的a得到的结果”这个短语是不完全的而且是无意义的，即它是一个不完全符号。而p/a；b代表一个确定的摹状词，它表达的意思是“那个独一无二的满足p/a；b！x 的x”，根据罗素的摹状词理论，这是一个不完全符号，而一个不完全符号自身是没有意义的，不可能代表一个实体。

对于作为逻辑主义基础的替代理论来说，它必须提供一个关于“类”的完整说明，并且用这个“类”来定义自然数。虽然根据罗素的观点，类表达式是不完全符号，它表明了类不是实体。

罗素用p/a来表示一个类。罗素认为“‘x是类p/a的一个元素’意味着‘用x替代p中的a所得到的结果’是真的”（［7］，第170页），即p/a；x是真的，使用替代理论的记法将其表示为：

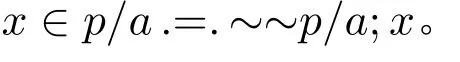
为了定义自然数，除了类这个概念之外，他还需要解释类的类这个概念。罗素把“类的类”定义为：

q/(p，a)是一个类的类 .=.(r)(c)(r′)(c′)(r/c=r′/c′.⊃：q/(p，a)；(r，c).=.q/(p，a)；(r′，c′)

在这个定义中，r/c=r′/c′表示的是两个类等同，它的意思是“无论x是什么，用x去替代r中的c所得到的结果等值于用x去替代r′中的c′所得到的结果。”（［7］，第169页）在上述类的类定义中，我们可以认为当q/(p，a)；(r，c)为真时，r/c是类的类q/(p，a)的一个元素，即一个类。以此类推，罗素得到了“类的类的类”的定义等。

有了类定义和类的类的定义，罗素便有了定义自然数的基础。

为了得到所有空集的类，也就是罗素定义下的“零”，罗素考虑了这样一个命题：

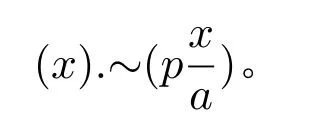
它的意思是：无论x是什么，用x去替代p中的a所得到的结果都是假的。罗素指出：“0是一个命题与一个实体之间的关系——无论我们把命题之中的那个实体替代为什么东西，其结果总是为假。”（［7］，第175页）根据罗素的这种观点，0可以定义为：

对于1，罗素的理解是“如果p/a只有一个元素，那么如果c就是那个元素，(p/a)；c是真的，并且当x不等于c时(p/a)；x是假的”（［7］，第176页）。因此根据罗素的这种论述，1可以定义为：

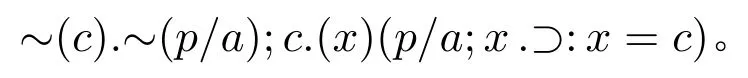
上述给出了自然数0和1在替代理论中的定义，有了最基本的自然数和定义自然数的方法，罗素的替代理论在一定程度上获得了成功。

3　替代悖论与替代理论的终结

在发现替代悖论之前，罗素曾经预见到：“到目前为止，唯一的致命危险就是从命题是实体的假设中我们可能发现悖论；但是我尚未发现这种悖论。”（［7］，第171页）遗憾的是，罗素最终发现了一个悖论，这就是p0/a0悖论，正是这个悖论让罗素最终放弃了替代理论而走向了分支类型论。p0/a0悖论的完整表述是：

罗素对替代悖论是这样描述的（［8］，第7页）：

罗素认为这个悖论摧毁了替代理论，这个悖论的出现最终促使罗素走上了类型论之路。在原手稿中，罗素并没有解释和论证这个悖论。依据第二部分给出的基本定义，本节将为这个悖论提供一个解释。

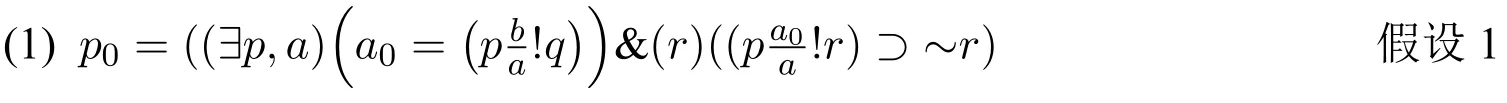
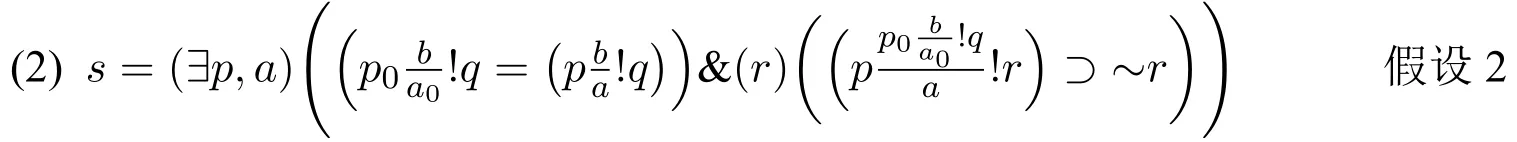
(3)假设s为假，根据否定定义和存在量词定义，可得下式为真

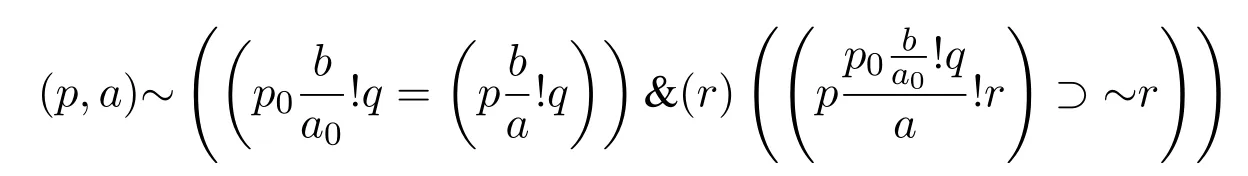
(4)根据全称概括规则，可用p0代替上式中的p，可用a0替代上式中的a，我们可以得到

(5)根据否定定义，我们可以看到下式为假

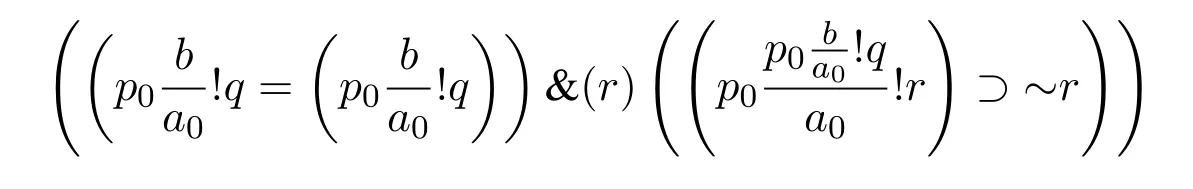
(6)由于第一个合取支为真，所以第二个合取支必然为假，即下式为假

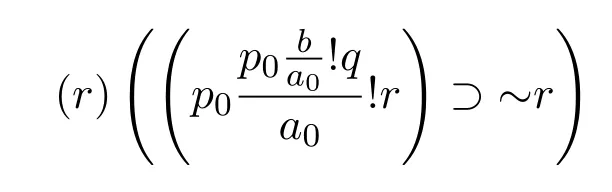
(7)由于r的取值范围是全体实体，所以令r=s，可得下式为假

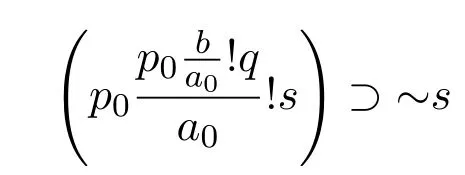
(8)由于蕴涵前件正是s的定义，所以前件为真，后件毕为假，即s为真，矛盾！

(10)根据全称消去规则，令r=s，可得下式为真：

(11)根据s的定义，此蕴涵前件为真，因此后件也为真，即s为假，矛盾。

虽然罗素对替代理论的哲学内涵讨论的不多，但是通过以上分析，我们还是得出两点重要结论。第一、在罗素的不完全符号理论中，类、函数、摹状词等不完全符号都没有单独的意义，但是命题是完全的，因此命题可以合法地出现在替代运算之中。第二、由于罗素坚持变元是非受限的，命题也是一种实体，也可以成为变元的值，他的替代理论最终仍然未能逃脱悖论的纠缠。罗素在手稿中也表达了对替代悖论产生原因的反思：“回避这个怪物的唯一方式就是针对命题创造一个类型学说，以至于在p0ba0！q，b和a都是在类型上低于p 和q。”（［8］，第7页）

替代悖论的发现产生了重要的影响：它不仅极大地影响了罗素的形而上学——罗素不再把命题当做实体，而且也摧毁了罗素关于悖论来自虚假抽象的观点。由于悖论的完全消失是罗素的悖论解答方案的“绝对必要”条件，一个依然存有悖论的理论显然是罗素无法接受的。这也导致了罗素开始重新思考悖论的统一形式问题，最终罗素接受了彭加莱的观点，即所有的悖论都具有自我指称的特点，并重新走向了类型论。

［1］ K.Gödel，1944，“Russell’smathematicallogic”，inP.BenacerrafandH.Putnam(eds.)，Philosophy of Mathematics，pp.447-469，Cambridge：Cambridge University Press.

［2］ I.Grattan-Guinness，1997，Dear Russell，Dear Jourdain:A Commentary on Russell’s Logic，Based on His Correspondence with Philip Jourdain，New York：Columbia University Press.

［3］ G.Landini，1998，Russell’s Hidden Substitutional Theory，Oxford：Oxford University Press.

［4］ B.Russel，1903，The Principles of Mathematics，London：George Allen and Unwin Press.

［5］ B.Russel，1959，My Philosophical Development，London：George Allen and Unwin Press.

［6］ B.Russell，1905，“On denoting”，Mind，14(56)：479-493.

［7］ B.Russell，1906，“On some difficulties in the theory of transfinite numbers and order types”，in D.Lackey(ed.)，Essays in Analysis，pp.135-164，London：George Allen and Unwin Ltd.

［8］ B.Russell，1906，“Onsubstitution”，RussellArchiveofMcMasterUniversity，Manuscript (RA 220.010950).

［9］ B.Russell，1994，“The foundations of mathematics”，in A.Urquhart(ed.)，The Collected Papers of Bertrand Russell，Vol.4，London and NewYork：Routledge.

［10］ 郑伟平，“论罗素《数学原则》中的联结词”，哲学研究，2009年第4期。

［11］ 郑伟平，“罗素《论指称》研究的一个教条”，厦门大学学报（哲学社会科学版），2012年第3期。

（责任编辑：崔建英）

Abstract

From 1903 to 1908，Russell developed the substitutional theory as a solution of paradoxes，and finanlly abandoned it.What Russell learned from his theory of definite description is that paradoxes are caused by false abstraction.The fundamental concept “substitution”may be applied to avoid false abstraction.By using it to define classes and functions，the substitutional theory was proved to be successful in some sense.Unfortunately，the emergence of the substitutional paradox made Russell give up the theory of substitution and embrace the ramified thoery of type.

Russell’s Substitutional Theory

Weiping Zheng
Department of Philosophy，Xiamen University
zhengweiping@xmu.edu.cn

B81

A

2015-01-19