RMI方法在线性代数中的应用
2016-10-08张德全刘静静
张德全+刘静静
【摘 要】阐述RMI方法的思想与含义,对RMI方法在大学线性代数课程中九个方面的应用进行探索。
【关键词】关系 映射 反演 RMI方法 线性代数 应用
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2016)07C-0131-04
关系(Relationship)、映射(Mopping)、反演(Inversion)方法是1983年由徐利治教授首先提出来的,简称RMI方法。RMI方法不仅是处理数学问题的一种具有普遍意义的思想方法,也是一切工程技术或应用科学部门中解决问题的普遍方法或工作原则。这个方法提出伊始就得到了广泛的重视和应用,由于现行大学数学教材中没有给出这个方法,本文首先简绍RMI方法,然后给出RMI方法在线性代数课程中的应用,试图帮助学生学好线性代数课程及大学数学课程的同时,使学生学会运用RMI这一科学方法。
一、RMI方法的思想与含义
概括地讲,RMI方法是指这样一个解决问题的过程;为了解决一个有困难的领域A中给定的问题x,设法将其映射(变换)成另一个领域B中的问题y,而y在领域B中则是易于解决的,当问题y解决之后,再映射(反演)回去,便得到领域A中给定问题x的解。笛卡尔发明解析几何可看作RMI方法的经典例子。如图1。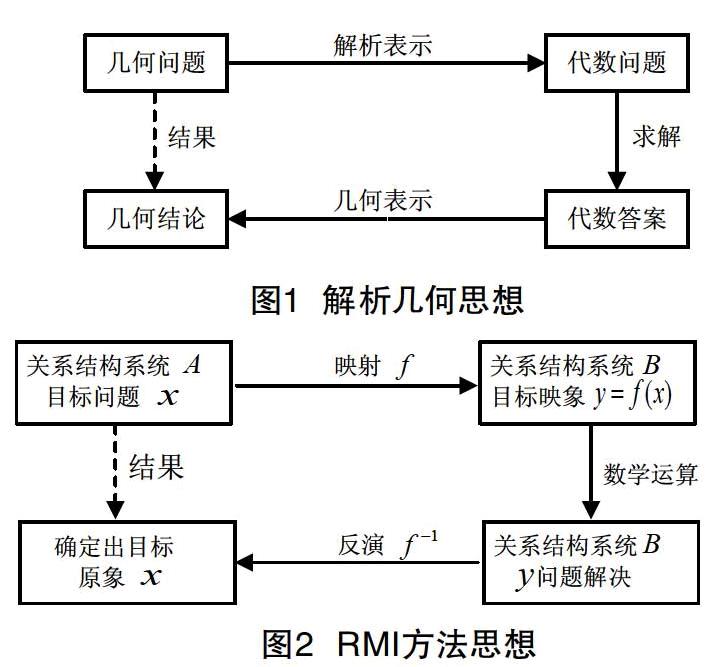
在数学中,RMI方法可描述为:在关系结构系统A中欲研究问题x,若存在较容易研究的关系结构系统B,并且有双射f,使B=f(A)、y=f(x),通过一定的数学方法,在B中把问题研究清楚,再通过x=f -1(x),反演出x,较容易地解决了问题x。如图2。
二、RMI方法在大学线性代数课程中的应用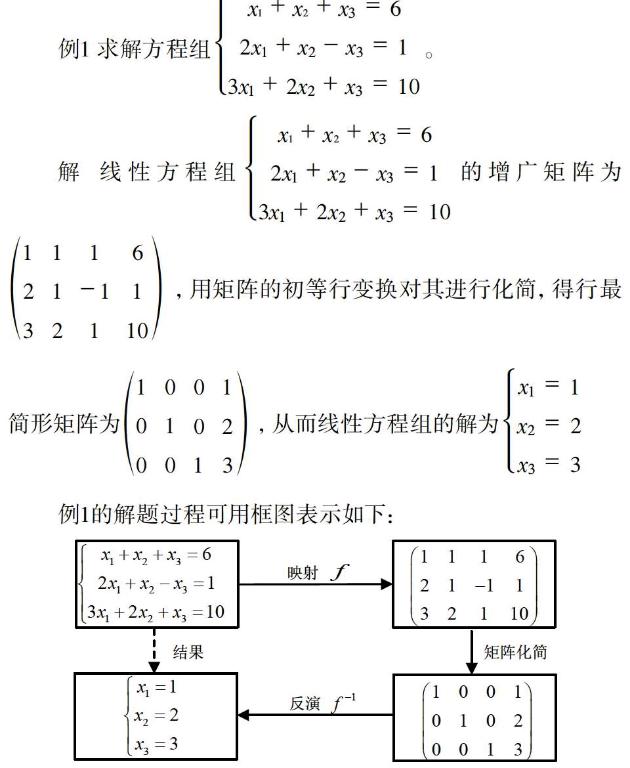
RMI方法在数学中,有着极为广泛的应用。本文就RMI方法在大学线性代数课程中的应用进行一些探索。由于RMI方法属于“化归”方法的范畴,为了叙述方便,对于使用RMI方法解决的问题,本文叙述为问题的“转化”解决。
(一)线性方程组的求解可转化为矩阵的化简
用初等方法求解线性方程组,对于未知量以及方程个数较多时是困难的。建立可逆映射f,将线性方程组与它的增广矩阵1-1对应,利用矩阵的初等行变换对增广矩阵进行化简,使之化为行最简形矩阵,就可对应得出原线性方程组的解。
例1 求解方程组。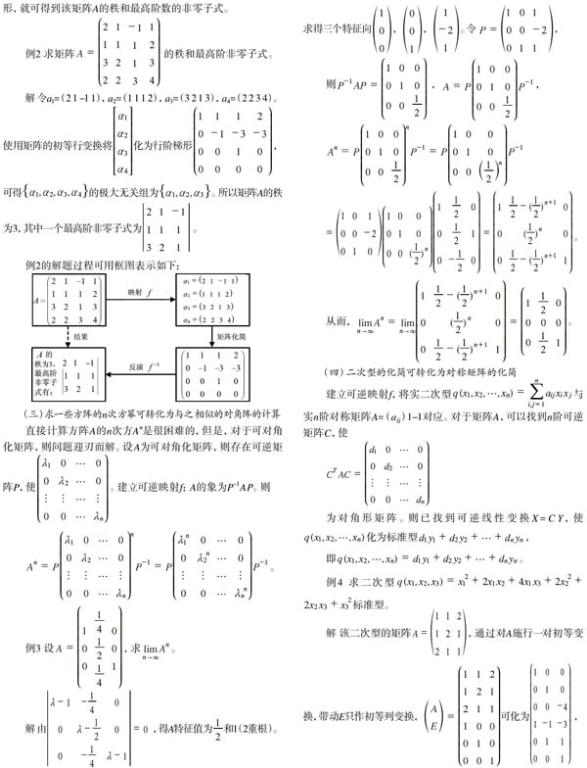
(二)求矩阵的秩可转化为求n维向量组的秩
按照矩阵的非零子式的最高阶数求矩阵的秩,几乎是一件不可能的事。建立可逆映射f,将矩阵Amn看成由矩阵Amn的m个行向量组成的向量组,利用向量组的初等变换不改变向量组的等价性,而等价向量组的秩相同。可将向量组△按行排成矩阵进行矩阵的初等行变换,使之化为行阶梯形,就可得到该矩阵A的秩和最高阶数的非零子式。
例2 求矩阵 的秩和最高阶非零子式。
(三)求一些方阵的n次方幂可转化为与之相似的对角阵的计算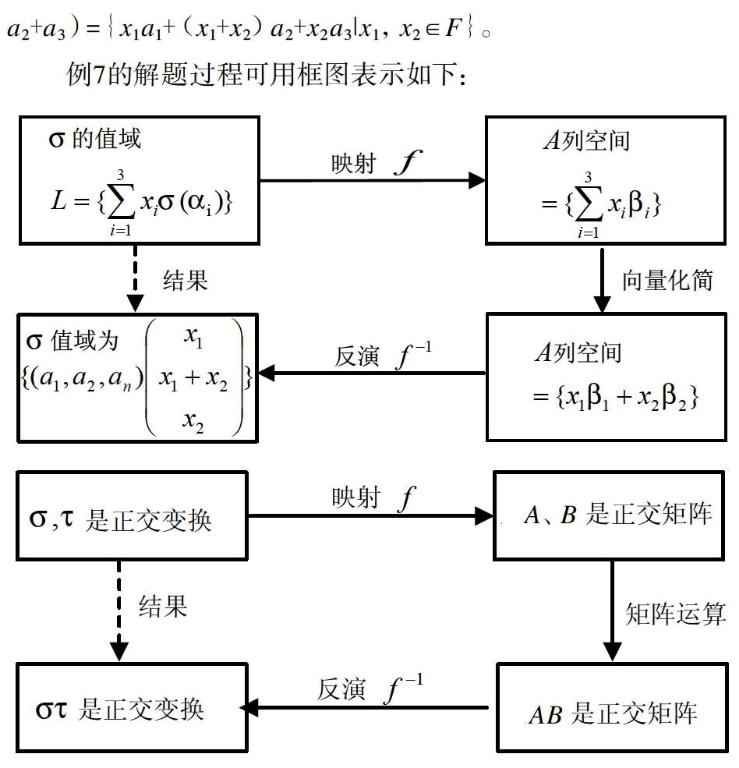
从以上可以看到RMI方法在线性代数课程教学中的作用和意义。作为数学教师,把RMI方法贯穿到高等数学的教学过程中去,教给学生RMI这一科学方法,进而培养学生的创造能力是我们应尽的职责。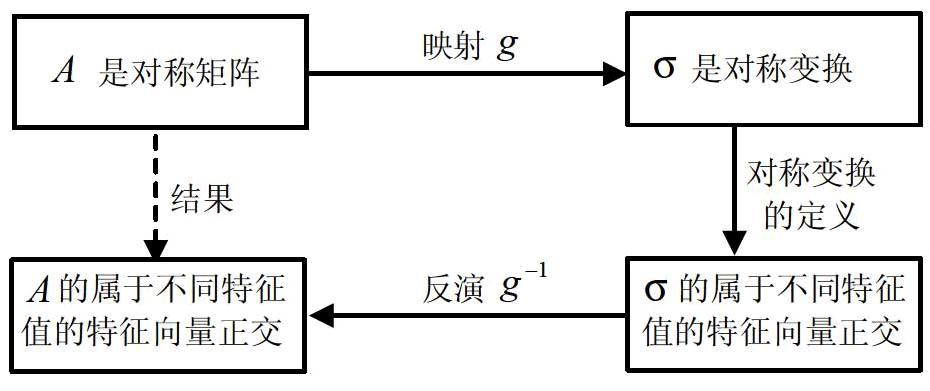
【参考文献】
[1]徐利治.数学方法论选讲[M].武汉:华中工学院出版社,1983
[2]程兰芳.数学中的“关系—映射—反演”方法[J].河北农业大学学报(农林教育版),1999(12)
[3]戴祥领.RMI方法在数学中的应用[J].遵义师范学院学报,2004(12)
[4]吴国泉.RMI方法在数学中的应用[J].牡丹江教育学院学报,2005(2)
[5]张德全 耿秀荣.线性代数[M].沈阳:东北大学出版社,2012
【基金项目】国家自然金数学天元基金(11326161);河南省教育厅重点科学研究项目计划(14A110011)
【作者简介】张德全(1959— ),男,河南漯河人,桂林航天工业学院教授,研究方向:组合数学;刘静静(1983— ),女,山东东营人,郑州轻工业学院数学与信息科学学院讲师,博士,研究方向:非线性色散波方程。
(责编 何田田)
