基于鲁棒的余弦欧氏距离度量降维的图像检索方法
2016-09-29黄晓冬孙亮
黄晓冬 孙亮


摘要:为解决主成分分析(PCA)无法处理非线性数据集以及鲁棒性差的问题,提出一种鲁棒的余弦欧氏距离度量的降维方法(RCEM)。该方法利用余弦度量(CM)能够处理离群点的特点来提取数据的局部几何特征,并利用欧氏距离能够很好地保持样本的方差信息的特点来刻画数据集的全局分布,在保留数据局部信息的同时实现了局部和全局的统一,提高了局部降维算法的鲁棒性,同时避免了局部小样本问题。实验结果显示,与角度优化全局嵌入(AOGE)方法相比,在Corel-1000数据集下检索查准率提高了5.61%,相比不降维时检索时间减少了42%。结果表明,RCEM算法能在不降低图像检索精度的同时提高图像检索的效率,可以有效应用于基于内容的图像检索(CBIR)。
关键词:主成分分析;余弦度量;欧氏距离;局部信息;基于内容的图像检索
中图分类号:TP391.41
文献标志码:A
0引言
近年来,随着多媒体技术和互联网图像资源的迅速发展,人们对图像检索的需求越来越强烈。图像检索技术主要分为基于文本的图像检索(Text-Based Image Retrieval, TBIR)和基于内容的图像检索(Content-based Image Retrieval, CBIR)方法。CBIR根据图像所包含的颜色、纹理、形状和空间位置信息等信息来描述特征,进而对高维低层视觉特征所形成的特征向量进行处理和检索,成功克服了TBIR中存在的关键字描述不准确以及检索效率不高等问题,是一种具有自动化和智能化特点的图像检索方法。图像特征提取的方法有很多,其中:Ojala等[1]提出将局部二进制模式(Local Binary Pattern, LBP)作为图像的纹理特征描述子;Liu等[2]提出的微观结构描述子(Micro-Structure Descriptor, MSD)方法用边缘定位来提取图像的微观结构;Feng等[3]提出了全局相关描述子(Global Correlation Descriptor, GCD)方法用来提取图像的颜色和纹理特征。然而,虽然图像特征相对于图像的原始数据而言数据量小得多,但是这些特征向量仍具有高维的特点,其计算量是巨大的,检索效率和速度往往让人无法忍受。因此,对这些高维向量进行降维非常有意义。
维数约简的本质在于寻找数据集内部固有的性质,以此来保持样本间的一些重要关系。例如在一些线性模型中,维数约简的主要思想就是保持样本间的某个全局关系[4]。经典的主成分分析(Principal Component Analysis, PCA)[5]希望投影到低维PCA子空间的数据方差最大,而多维尺度变换(Multi-Dimensional Scaling, MDS)[6]则希望保持样本间相似性最大。
针对上述线性算法难以处理非线性数据的问题,下列算法解决了非线性数据集的学习问题:局部线性嵌入(Locally Linear Embedding, LLE)算法[7]假设数据局部是线性的,通过寻找每个样本的k最近邻来尽可能保持数据集降维前后的局部线性结构,最终实现了对非线性数据的嵌入;随后,Zhang等[8]提出的局部切空间排列(Local Tangent Space Alignment, LTSA)算法在LLE的基础上对每个样本局部进行PCA降维,对计算出的每个邻域的局部切空间坐标进行全局排列,得到全局的低维流形。但以上算法由于缺少对数据集全局结构的把握,并且对噪声比较敏感,容易受到奇异点的干扰,往往导致降维后数据产生严重的几何形变。等距映射Isomap[9-11]在保持MDS中样本相似性最大的基础上,利用最短路径近似样本间的测地线距离,实现了局部与全局的统一。Laplacian 特征映射(Laplacian Eigenmap, LE)[12]通过利用高斯核函数构造样本近邻图,得到稀疏的邻接矩阵,使目标函数保持这种图结构来达到降维的目的。
以上非线性降维算法分别从不同的角度刻画了高维数据的特征,但由于采用隐式的学习方式,因此没有明确高维到低维数据的映射关系,限制了这些算法在图像检索等领域的应用,导致其学习非线性数据集的优势无法充分体现。为更好地解决实际应用问题,近几年相继提出了局部保持投影(Locality Preserving Projection, LPP)[13]、邻域保持嵌入(Neighborhood Preserving Embedding, NPE)[14]、正交的邻域保持投影(Orthogonal Neighborhood Preserving Projection, ONPP)[15]以及线性的局部切空间排列(Linear Local Tangent Space Alignment, LLTSA)算法[16]等能够提取局部信息的线性降维算法,这些算法与已有的非线性算法相对应,将高维数据映射到低维子空间的非线性隐式映射明确为一种线性映射。
由于已知的映射关系在很多实际应用中是必要的,上述算法通过全局的线性化成为解决此问题的一种有效途径,但往往面临局部小样本问题,即待分解的矩阵不可逆。PCA作为一种经典的学习方法,能够避免上述问题;但PCA存在只能局限于处理在几何上呈线性分布或近似线性分布的数据集以及对含噪声的数据集的学习效果不理想的问题。
针对PCA的不足,很多学者作出了相关改进。为了提高PCA的鲁棒性,De la Torre等[17]提出了Robust PCA,Choulakian[18]提出了L1-范数投影PCA;为了使PCA能够处理非线性分布的数据集,Schlkopf等[19-20]通过将核函数引入PCA算法,并将数据映射到特征空间计算主成分,以此得到Kernel PCA;Yang等[21]提出的局部PCA(Local Principal Component Analysis, LPCA)算法,在保留数据的局部信息的同时,利用整体的线性化刻画了数据的全局信息,从而使其能够处理新样本。
为了提高局部降维方法的鲁棒性,同时避免局部小样本问题,本文利用角度优化全局嵌入(Angle Optimization Global Embedding, AOGE)算法[22]鲁棒性较强的特点,通过局部正交投影方法提出一种鲁棒的基于角度余弦和欧氏距离度量的降维方法——RCEM(Robust Cosine-Euclidean Metric)。实验结果表明,该方法能够有效应用于CBIR,不仅能够提高图像检索的效率,而且基本没有降低图像检索的精度。
2基于RCEM算法的图像检索方法
2.1RCEM理论分析及算法
图像检索的特征数据一般采用直方图量化特征,文献[22]分析了在含噪声数据中,基于角度的AOGE比PCA具有更强的抗噪能力,因此,余弦能够发挥较好的度量效果。进一步,本文提出的RCEM算法主要利用余弦能够处理离群点,欧氏距离能够很好地保持样本方差信息的特点。同时,考虑到数据集分布的复杂性,余弦部分受到LPCA[21]提取数据局部结构方法的启发,利用局部余弦度量保持数据集度量信息的最大化,而在欧氏距离部分利用全局度量保持数据集度量信息的最大化,进而获得更好的效果。
2.2基于RCEM算法的图像检索
图2介绍了基于RCEM的CBIR系统的工作流程。CBIR先通过检索和索引步骤提取每幅图像的低层视觉特征向量,利用RCEM降维算法得到低维特征向量,然后与数据库中的对应特征向量进行相似性比较,依据最接近的匹配得分得到相似的检索图片,最终在检索图片中得到目标图片。
3实验结果及分析
利用三种图像检索数据集和核AOGE(Kernel AOGE, K-AOGE)、RCEM两种降维方法以及不降维方法对本文所提出的基于RCEM算法的图像检索方法进行评估。考虑数据集特征的非线性情况,核AOGE在AOGE的基础上加入高斯核函数。
3.1实验设置
实验采用的三种图像数据集包括Corel-1000、Corel-10000和Coil-100,示例如图3。Corel-1000包含10类总计1000张图片,有汽车、恐龙、食物等;Coil-100数据库共有100个物体,每个物体从0°至360°水平旋转拍摄,共72幅图像;Corel-10000和Coil-100比Corel-1000更大。三个数据库的基本信息如表1所示。
在下面的实验中,以局部二进制模式(LBP)纹理直方图作为纹理特征给出每幅图像的特征向量,维数为256;本文令邻域参数k=4,d=100,α=0.65,高斯核函数宽度参数σ=1;“DR method”表示降维方法,不降维的方法标记为“DR-Free”;“检索时间”表示检索数据集所用的时间。
3.2实验结果及分析
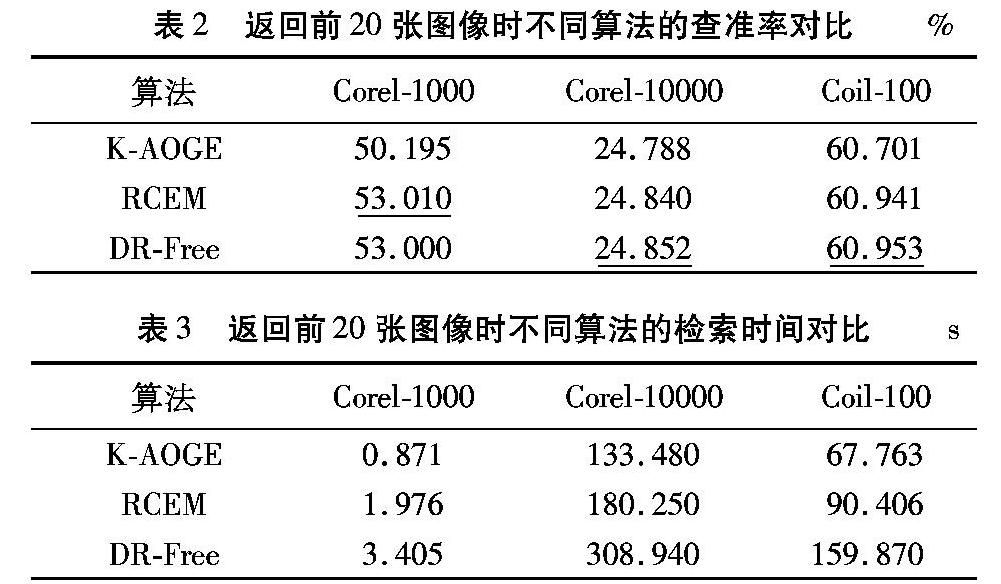
通过表2,可以看到本文所提方法能够有效应用于图像检索,当选择LBP特征描述符进行降维并返回20幅图像时,尤其在Corel-1000数据集中,RCEM比K-AOGE算法的检索准确率更高,相比不降维时的情况也相差很小,这主要是因为RCEM同时考虑了角度和欧氏距离度量的优化,在提取数据局部信息的同时,较好地实现了局部和全局的统一。通过表3,可以看到RCEM和K-AOGE都能够显著提高图像检索的效率,而RCEM相比K-AOGE速率略微降低,这主要是因为其需要对数据集的每一个样本数据的局部信息进行提取和计算,因此时间复杂度有所增加。
4结语
本文深入分析了线性降维算法PCA及局部形式LPCA,针对角度优化的全局嵌入降维算法AOGE提出了一种鲁棒的余弦欧氏距离度量的降维算法RCEM,并将其用于CBIR系统中。RCEM采用余弦度量提取数据集的局部信息,并采用欧氏距离刻画数据集的全局分布,实现了局部和全局的统一。基于标准数据集下的实验结果表明RCEM比AOGE的方法更有效,能够提高图像检索的效率。
参考文献:
[1]OJALA T, PIETIKINEN M, MENP T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(7): 971-987.
[2]LIU G-H, LI Z-Y, ZHANG L, et al. Image retrieval based on micro-structure descriptor [J]. Pattern Recognition, 2011, 44(9): 2123-2133.
[3]FENG L, WU J, LIU S, et al. Global correlation descriptor: a novel image representation for image retrieval [J]. Journal of Visual Communication and Image Representation, 2015, 33: 104-114.
https://www.researchgate.net/publication/282408527_Global_Correlation_Descriptor_A_novel_image_representation_for_image_retrieval
[4]FENG L, LIU S-L, WU Z-Y, et al. Maximal similarity embedding [J]. Neurocomputing, 2013, 99: 423-438.
[5]JOLLIFFE I T. Principal Component Analysis [M]. New York: Springer-Verlag, 1986: 10-28.
Springer Series in Statistics
[6]SUN J, CROWE M, FYFE C. Extending metric multidimensional scaling with Bregman divergences [J]. Pattern Recognition, 2011, 44(5): 1137-1154.
http://xueshu.baidu.com/s?wd=paperuri%3A%28ffcd39def00552a137af1f80c7e74053%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fwww.sciencedirect.com%2Fscience%2Farticle%2Fpii%2FS0031320310005406&ie=utf-8&sc_us=1549776567823179089
[7]ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding [J]. Science, 2000, 290(5500): 2323-2326.
[8]ZHANG Z, ZHA H. Principal manifolds and nonlinear dimensionality reduction via Tangent space alignment [J]. Journal of Shanghai University (English Edition), 2004, 8(4): 406-424.
SIAM Journal on Scientific Computing, 2005, 26(1): 313-338.
http://xueshu.baidu.com/s?wd=paperuri%3A%28c94b8b8b1f97b351da7242d84829190f%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fdl.acm.org%2Fcitation.cfm%3Fid%3D1039898%26preflayout%3Dflat&ie=utf-8&sc_us=13023074109172339473
[9]TENENBAUM J B, DE SILVA V, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction [J]. Science, 2000, 290(5500): 2319-2323.
[10]BALASUBRAMANIAN M, SCHWARTZ E L. The isomap algorithm and topological stability [J]. Science, 2002, 295(5552): 7.
[11]SAXENA A, GUPTA A, MUKERJEE A. Non-linear dimensionality reduction by locally linear isomaps [C]// ICONIP 2004: Proceedings of the 11th International Conference on Neural Information Processing, LNCS 3316. Berlin: Springer-Verlag, 2004: 1038-1043.
[12]BELKIN M, NIYOGI P. Laplacian eigenmaps for dimensionality reduction and data representation [J]. Neural Computation, 2003, 15(6): 1373-1396.
[13]HE X, NIYOGI P. Locality preserving projections [C]// Advances in Neural Information Processing Systems 16. Cambridge, MA: MIT Press, 2004: 153.
http://www.iipl.fudan.sh.cn/~zhangjp/literatures/MLF/TR-2002-09.pdf
[14]HE X, CAI D, YAN S, et al. Neighborhood preserving embedding [C]// ICCV 2005: Proceedings of the Tenth IEEE International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2005: 1208-1213.
[15]KOKIOPOULOU E, SAAD Y. Orthogonal neighborhood preserving projections [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 29(12): 2143-2156.
ICDM 05: Proceedings of the Fifth IEEE International Conference on Data Mining.
https://infoscience.epfl.ch/record/87294/files/Kokiopoulou2005_1351.pdf
Pages 234-241
[16]ZHANG T, YANG J, ZHAO D, et al. Linear local tangent space alignment and application to face recognition [J]. Neurocomputing, 2007, 70(7/8/9): 1547-1553.
[17]DE LA TORRE F, BLACK M J. Robust principal component analysis for computer vision [C]// ICCV 2001: Proceedings of the Eighth IEEE International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2001, 1: 362-369.
[18]CHOULAKIAN V. L1-norm projection pursuit principal component analysis [J]. Computational Statistics & Data Analysis, 2006, 50(6): 1441-1451.
[19]SCHLKOPF B, SMOLA A, MLLER K-R. Kernel principal component analysis [C]// ICANN 97: Proceedings of the 7th International Conference on Artificial Neural Networks, LNCS 1327. Berlin: Springer-Verlag, 1997: 583-588.
[20]SCHLKOPF B, SMOLA A, MLLER K-R. Nonlinear component analysis as a kernel eigenvalue problem [J]. Neural Computation, 1998, 10(5): 1299-1319.
[21]YANG J, ZHANG D, YANG J-Y. Locally principal component learning for face representation and recognition [J]. Neurocomputing, 2006, 69(13/14/15): 1697-1701.
[22]刘胜蓝,闫德勤.一种新的全局嵌入降维算法[J].自动化学报,2011,37(7):828-835. (LIU S L, YAN D Q. A new global embedding algorithm[J]. Acta Automatica Sinica, 2011, 37(5): 828-835.)
[23]AGGARWAL C C, YU P S. Outlier detection for high dimensional data [J]. ACM Sigmod Record, 2001, 30(2): 37-46.
[24]YAN D, LIU S. An angle optimized global embedding algorithm [C]// FSKD 2010: Proceedings of the Seventh International Conference on Fuzzy Systems and Knowledge Discovery. Piscataway, NJ: IEEE, 2010, 4: 1843-1847.
