П理论在超超临界汽轮机组回热系统高压加热器变工况的建模研究和试验分析

于忠平， 胥建群

(1. 东南大学 能源环境学院， 南京 210019；　2. 大唐南京发电厂， 南京 210057)



П理论在超超临界汽轮机组回热系统高压加热器变工况的建模研究和试验分析

于忠平1,2， 胥建群1

(1. 东南大学 能源环境学院， 南京 210019；2. 大唐南京发电厂， 南京 210057)

从Buckingham理论出发，基于高压加热器实际测量数据，建立无量纲数的数学模型(П理论)，反映高压加热器的变工况运行。该模型应用于某660 MW超超临界汽轮机组高压加热器上的实践表明：计算结果与实际数据偏差很小，可为同类型机组提供参考。

发电厂； П理论； 高压加热器； 变工况

抽汽回热系统是发电厂原则性热力系统最基本的组成部分，利用在汽轮机做过部分功的蒸汽加热给水，提高了给水温度，减少了锅炉受热面的传热温差，从而减少了给水加热工程中的不可逆损失，在锅炉中的吸热量也相应减少。抽汽回热系统的正常投运对提高机组的热经济性具有决定性的影响。

现在大型汽轮机组一般配置3台高压加热器(简称高加)、4台低压加热器和1台除氧器。在大多数情况下，加热器加热的是过热蒸汽。加热器包含3段可以有效利用从蒸汽到饱和水变化释放的热量。在第一段，过热蒸汽被冷却成饱和蒸汽；在第二段，饱和蒸汽释放汽化潜热冷凝成水；在第三段，冷却水过冷释放热量加热介质[1]。由于现在加热器存在的三个区域和介质状态的变化，加热器的运行工况比较复杂。目前有两种较为流行的描述加热器的数学模型：第一种数学模型中，三段并不区别对待，数学模型包含能量守恒定律和传热方程，该模型将传热系数假设为常数或者是雷诺数和普朗特数的一个函数；第二种数学模型按照常例将加热器分成三段，并且每一段应用能量守恒定律和传热方程，讨论每一段的传热系数[2]。

传热系数主要基于一些无量纲常数，比如雷诺数和普朗特数，传热系数的相似原则可以运用在一定范围内参数变化的运行工况，但不太准确。

目前对回热加热器的变工况描述的数学模型将加热器分成四段或者六段，但这种模型更加复杂。在所有数学模型中都是以求得传热系数为目的，笔者努力寻求基于实际测量数据的回热加热器的变工况数学模型，该模型中不包括传热系数。

1　回热系统加热器变工况的数学模型

1.1 系统概述

笔者主要分析某660 MW超超临界汽轮机的第一级高加，该汽轮机回热系统高加简图见图1。

Th1—1号高加抽汽温度；mk—1号高加抽汽流量；Th2—1号高加疏水温度；Tc1—1号高加进水温度；mc—给水流量；Tc2—1号高加出水温度。

图1回热高加系统简图

1.2 数学模型的建立

为求得加热器出口被加热的给水出口温度，采取Buckingham理论的参数分析法[3]。

f(Q1,Q2,Q3,…,Qn)=0

(1)

为了选择高压回热加热器的不相关参数，考虑一个给定的从蒸汽到水的加热器(高压加热器中的一段)，采用能量平衡方程和传热方程描述换热器该段的传热方程[4-5]。

Q=Ch(Th1-Th2)=Cc(Tc2-Tc1)

(2)

Q=KAΔT

(3)

分析式(2)和式(3)的关系显示：换热器的出口水温由进入换热的介质温度(Th1，Tc1)，介质的热容(Ch，Cc)、传热系数K和换热面积A来决定。

Tc2=f(Th1,Tc1,Ch,Cc,K,A)

(4)

流体的热容等于比定压热容和介质流量的乘积。传热系数是加热器进口流体温度和流量的函数。

所以加热器出口温度函数(4)可以被认为是加热器进口介质流体温度、流量和换热面积的函数。

Tc2=f(Th1,Tc1,mh,mc,K,A)

(5)

加热器的其他两段也可以用此方法近似分析，所以高加的出口水温可以写成：

Tc2-Tc1=f(Th1-Tc1,mh,mc,A)

(6)

无量纲分析方法可以用在这种无相关性参数的地方。更进一步，无量纲分析可以被写作：

Tc2-Tc1=C(Th1-Tc1)a(mh)b(mc)cAd

(7)

比较相关单位的指数可以解得：

a=1，c=-b，d=0

代入式(7)中可得：

Tc2-Tc1=C(Th1-Tc1)1(mh)b(mc)-bA0

(8)

可以将式(8)整理成[6]：

(9)

引进两个无量纲参数：

(10)

(11)

所以式(7)可以写成如下形式：

П1=f(П2)

(12)

在上述分析的基础上确立了两个无量纲参数的函数关系，这两个无量纲参数和换热器进口介质温度、流量和换热器出口水温相关。高加的上述函数的具体形式要建立在实际测量数据基础上。

2　数学模型的实际运用

应用该模型时，换热器需要测量的参数有加热蒸汽压力和温度，凝结温度，被加热水进、出口水温和流量。1号高加抽汽流量可以用能量守恒方程求得：

(13)

式中：ic2为高加出水焓；ic1为高加进水焓；ih1为高加进汽焓；ih2为高加疏水焓。

由于2、3号高加有上一级疏水流入，情况更加复杂，下面以1号高加为例来计算。

首先取设计的热力性能在TRL、100%、75%、50%、40%负荷点的设计数据，参照以上无量纲分析方法进行计算，得出П1和П2的关系见图2。

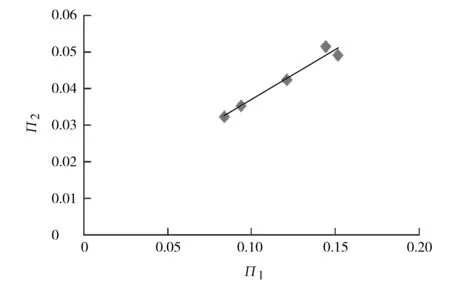
图2　汽轮机组设计数据无量纲数的函数关系

由图2可见：П1和П2成线性关系，П2=0.274 5П1+0.009 6。

根据1号高加实际运行中的测量参数，采集机组运行的一天数据，每5 min采集一组，一共287组数据，计算П1和П2，并求得两个无量纲数之间的函数关系(见图3)。

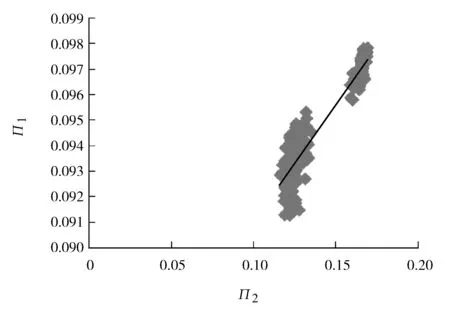
图3　实际运行参数计算的П1和П2函数关系

由图3可见：П1和П2线性相关性较弱，呈曲线关系。分析主要原因是负荷波动所致，图中数据群断开是因为当天是性能试验，数据集中在660 MW和450 MW，中间一段数据缺失的原因。

分析实际运行数据、设计数据以及数学模型的偏差，在实际运行中，由于电网调度、煤种变化和运行水位调整等多方面的因素影响，工况其实是在不断变化的过程中。高加的介质流量、运行参数和负荷紧密相关，上述数学模型在实际应用时应考虑负荷的修正，因此公式(8)中的常数C引用成和负荷成关系的数。

(14)

式中：Pe为实际负荷；P0为额定负荷。

(15)

从实际数据计算，得出该函数关系(见图4)。

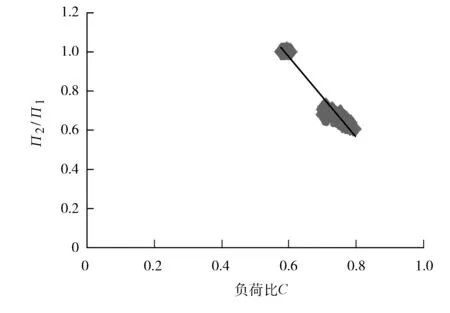
图4　修正后的П2/П1和负荷比的函数关系

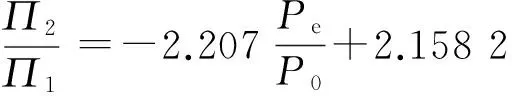
如果用该式来计算1号高加出口温度，和实际温度的对比结果见图5。

图5　出水温度计算值和测量的关系

由图5可见：1号高加出水温度计算值和实际测量值变化趋势一致，但存在偏差。研究出水温度的计算值和测量值的相关性，见图6。

图6　1号高加出水温度计算值和测量值的函数关系

由图6可见：1号高加出水温度的测量值和计算值线性相关性很强，用该线性关系来修正出水温度的计算值后，计算值和测量值的误差很小，最大误差为+0.15%。为验证修正关系的正确性，用该修正后的高加出水温度修正公式来计算另外一天的1号高加出水温度，且未去除工况变化剧烈点，发现最大误差为0.78 K，误差范围为0.28%(见图7)。

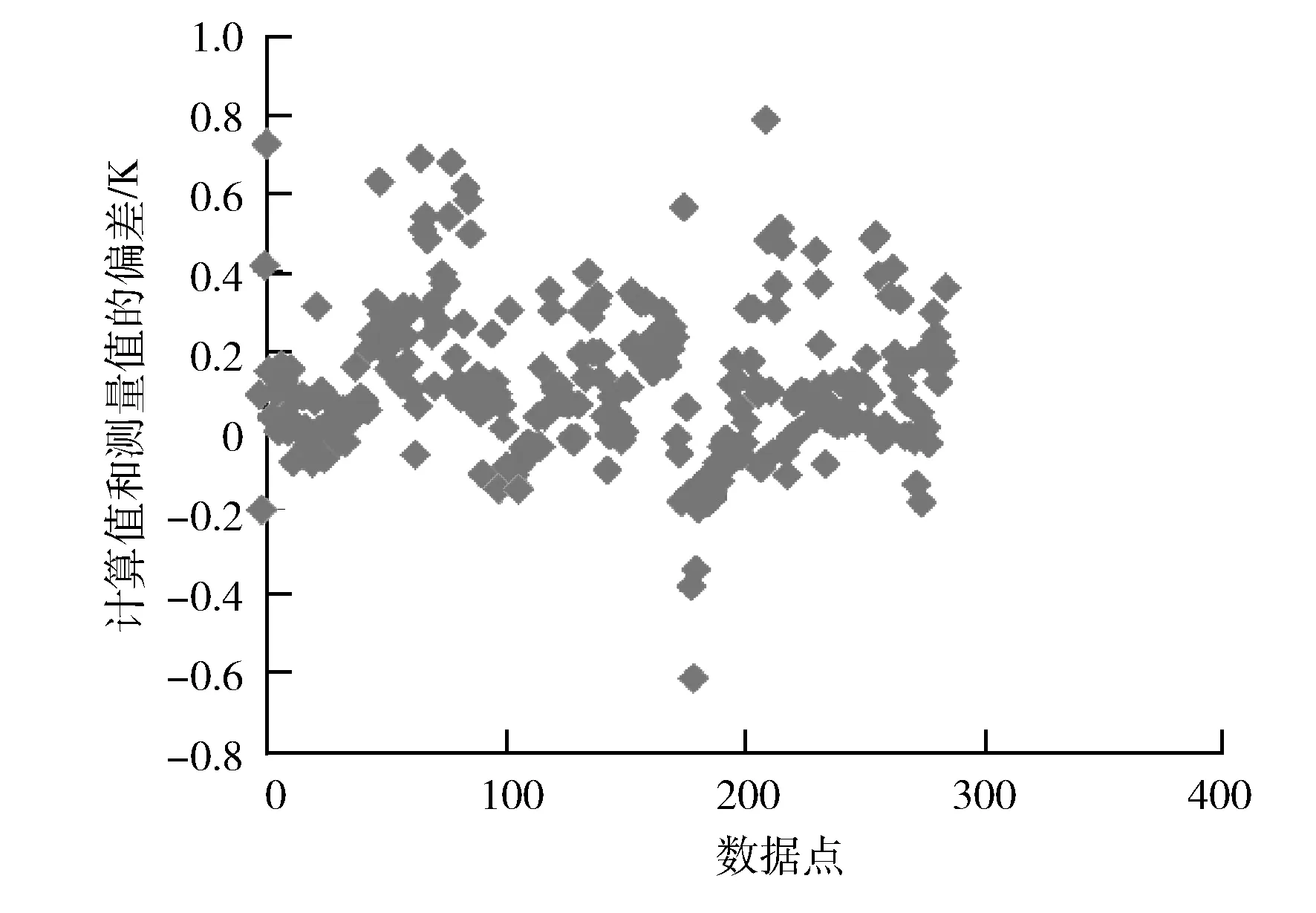
图7　1号高加另一天的出水温度计算值和测量值的偏差曲线

由图7可见：修正后的计算公式在机组50%～100%负荷变化时，和实际测量数据拟合度基本一致，绝对误差范围在-0.6～0.8 K，且集中在-0.2～0.2 K，相对误差为-0.2%～0.28%。

3　П理论应用于高压加热器数学模型研究的推广意义

鉴于应用П理论建立的模型在高加变工况运行应用上的准确性，进一步考虑将该模型计算被用于判断高加的实际运行状况分析，包括加热器泄漏、加热器清洁度以及高加三通阀内漏等问题。用实际数据和计算结果的偏差来提前分析判断属于何种故障，并利用检修机会进行检查处理验证，提高整个机组的回热效率。比如加热器清洁度恶化导致端差变大，则П1相对变小，П2/П1相对变大，曲线应相对于正常曲线平移等。这部分的工作需要结合机组大修前后数据的对比和理论分析进行对比得出，通过计算分析给运行机组提出参考意见。

4　结语

建立高加在变工况运行时的数学模型是复杂的，因为在高加的三段中的热交换包含蒸汽和水、冷凝蒸汽和水、疏水冷却和水。为了获得令人满意的高加变工况运行数学模型，加热器必须分为三段考虑各种介质的传热系数。传热系数主要基于一些无量纲常数，比如雷诺数和普朗特数，应用传热系数的关系依赖于加热器参数的变化范围以及介质特性，这比包含迭代的模型更加复杂。应用Buckingham理论研究建立一个基于实际测量数据的回热系统高压加热器模型，选择一系列测量数据用于无量纲参数的函数关系，来描述加热器的变工况运行。从以上计算结果分析，上述数学模型是非常有效的，最终误差在0%～0.29%。该计算模型在实际应用中误差可控，且可以进一步将计算结果应用于判断回热系统设备故障。

[1] 杨涛,胥建群,周克毅,等. 电站给水加热器水位的优化运行[J]. 东南大学学报(自然科学版),2012,42(S2):314-319.

[2] 赵文升,王兵树,马良玉,等. 大型火电机组加热器动态数学模型的研究[J]. 汽轮机技术,2001,43(6):324-327.

[3] YOUNG D F, MUNSON B R, OKIISHI T H, et al. A brief introduction to fluid mechanics[M]. 5th ed. London: John Wiley & Sons, Inc., 2011:238-273.

[4] 沈维道,蒋智敏,童钧耕. 工程热力学[M]. 3版. 北京:高等教育出版社,2001:52-56.

[5] 杨世铭,陶文铨. 传热学[M]. 4版. 北京:高等教育出版社,2006:5-6.

[6] LASKOWSKI R M. The application of the Buckingham П theorem to modeling high-pressure regenerative heat exchangers in off-desing operation[J]. Journal of Power of Technologies, 2011, 91(4):198-205.

Modeling of HP Regenerative Heat Exchanger in Ultra-supercritical Steam Turbine Unit under Variable Conditions based on П Theory

Yu Zhongping1,2, Xu Jianqun1

(1. School of Energy and Environment, Southeast University, Nanjing 210019, China;2. Datang Nanjing Power Plant, Nanjing 210057, China)

A non-dimensional mathematical model (П theory) was built up for high-pressure regenerative heat exchanger according to actual measurements based on Buckingham theory to reflect its operation status under variable working conditions, which was then applied to the HP heater of a 660 MW ultra-supercritical steam turbine unit. Application results prove the model to be accurate, which may serve as reference for similar units.

power plant; П theory; HP heater; variable working conditions

2015-11-09

于忠平(1985—)，男，助理工程师，主要从事电厂运行工作。

E-mail: ponpai@sohu.com

研究与分析

TM621.4

A

1671-086X(2016)04-0215-04