型钢混凝土柱承压性能非线性有限元分析

2016-09-28王震强

甘肃科技 2016年15期

关键词：筋率型钢承载力

王震强

（甘肃省交通规划勘察设计院有限责任公司，甘肃兰州730030）

型钢混凝土柱承压性能非线性有限元分析

王震强

（甘肃省交通规划勘察设计院有限责任公司，甘肃兰州730030）

从型钢混凝土本构关系入手引入接触面粘结滑移机制，讨论了在ANSYS模型中引入接触面粘结滑移机制模拟型钢混凝土柱的基本理论和具体方法。通过有限元模拟结果与已有文献实验结果地对比分析，验证了本研究所采用的ANSYS模型模拟型钢混凝土柱进行承压性能分析的可靠性和准确性。对影响型钢混凝土柱承压性能的三个因素（配筋率、混凝土强度、含钢率）进行了有限元模拟分析，得出了各因素对刚度、延性和承载力三方面的影响规律。研究表明：混凝土强度变化对构件刚度有所影响；在一定范围内，含钢率的增加可以有效提高构件的承载力；混凝土强度和配筋率的提高对改善构件延性有利。结论对型钢混凝土承压柱的工程应用具有一定的指导意义。

结构工程；型钢混凝土；承压性能；非线性有限元；粘结滑移；ANSYS

1　概述

型钢混凝土柱构件是由型钢、纵筋、箍筋及混凝土组合而成，即核心部分有型钢结构构件，其外部则为以箍筋约束并配以适当的纵向受力钢筋的混凝土结构。型钢混凝土柱中，型钢与混凝土共同作用，可以充分发挥两种材料的优点。与钢筋混凝土框架柱和钢结构相比，型钢混凝土承压柱具有截面小，承载力高；抗震及变形性能好；耐火性、耐久性好；有效改善混凝土性能；经济效应显著等优点。近30年来，随着我国经济的快速发展，城市建设步伐的加快，对于型钢混凝土柱的应用也越来越多，越来越频繁。

型钢混凝土柱是由两种性质不同的材料—混凝土和型钢组合而成的，型钢混凝土柱承压能力很大程度上依赖于这两种材料接触面处的粘结滑移性能，特别是在非线性阶段。因此，要对型钢混凝土柱承压进行系统全面的研究必须综合考虑材料的不均匀性、混凝土应力应变关系，裂缝开展、粘结滑移破坏等各种因素的影响。传统的试验方法成本较高，费时费力，在实验室进行试验研究很难对这些因素进行大量的、细致的、全面的分析。有限元理论的发展和有限元技术的应用为研究型钢混凝土柱构件复杂受力性能提供了一种有效的研究方法。文章利用大型通用有限元分析软件ANSYS，从型钢混凝土本构关系入手引入接触面粘结滑移机制，对型钢混凝土柱受压试验过程进行模拟与计算，根据所获得的构件的应力应变发展、破坏形态、荷载位移曲线、极限荷载等模拟结果，分析有关参数的变化对构件整体受力性能的影响，同时根据从加载至破坏的全过程非线性分析，深入分析各个参数变量对型钢混凝土柱受力性能的影响程度，找出在今后设计及工程应用中应加以重视的控制因素。

2　型钢混凝土承压柱非线性模型的建立与验证

2.1模型基本材料参数

文章研究的重点在于型钢混凝土柱受压性能与型钢混凝土粘结滑移关系的有效模拟，对于钢筋单元由于型钢混凝土柱在破坏时，钢筋与混凝土之间粘结性能较好，未出现滑移现象，不需考虑两者之间的相对作用，故在建立模型时采用分离式模型，分别建立混凝土与钢筋单元，但不考虑钢筋与混凝土之间的连接单元，两者共用节点。

在进行ANSYS有限元分析时，混凝土采用Solid65单元进行模拟，并依据不同的强度等级，选取相应的弹性模量，泊松比取为0.2，混凝土密度定义为2400kg/m3。本构关系选用非线性弹性本构模型，具体使用的是没有应变软化段的Saenz公式［1］。而混凝土破坏准则则采用William-Warnke五参数强度模型，其中裂缝张开剪力传递系数设为0.4，裂缝闭合剪力传递系数设为0.75，单轴抗压及抗拉强度采用混凝土强度设计值。为了使计算收敛，只考虑混凝土开裂，不考虑混凝土单元压碎状态，将单轴抗压强度项设为-1，以模拟低静水围压［2］。

模型中纵筋和横向箍筋选取Link83-D杆单元，型钢和实验垫板选取Solid45实体单元。用ANSYS进行分析时钢筋和横向箍筋采用双线性随动强化模型（BKIN），对应于弹性强化本构模型；型钢采用多折线性随动强化模型（MKIN），对应于弹塑性强化本构模型。具体输入的参数详见表1。

表1　ANSYS程序下钢筋和型钢材料输入参数表

模拟分析时在型钢混凝土柱两端设置了厚20mm的钢垫板。该实验垫板采用理想弹塑性本构模型，弹性模量提高2个数量级设置为2.0× 107MPa，其作用在于将钢垫板假设为理想刚体，从而在一定程度上消除应力集中现象［3］。

针对于型钢与混凝土之间的粘结滑移性能在两者之间设置了粘结滑移单元，用于更真实的模拟型钢混凝土柱的受力性能。粘结滑移单元采用了Combine39［4］非线性弹簧单元，该单元具有两个节点，在ANSYS程序使用中通过实常数F（力）-D（变形）曲线来定义非线性弹簧的受力实质，无需再额外定义材料性质，如图1所示。

图1　Combine39非线性弹簧单元

本构模型选取了西安建筑科技大学杨勇［5］通过大量推出试验所定义的粘结滑移本构关系，该本构关系建立的出发点就是为了解决型钢混凝土有限元模拟，具有较好的实用性。

引入模型时将依据试验测量的荷载～加载端滑移曲线（P～Sl曲线如图2所示），通过统计回归及数学描述转化成反映主要锚固条件（混凝土强度等级、混凝土保护层厚度、横向配箍率、锚固长度）的与加载端滑移的基准本构曲线τ～Sl。实际应用过程中需要根据型钢不同位置的受力特点对确定的平均粘结强度进行修正，最终建立适用于有限元分析的粘结滑移本构模型。

图2　P～Sl曲线的简化模型

在接触节点设置弹簧单元时，为全面考虑型钢与混凝土连接面上的相互作用，在连接面上对应节点之间采用三个弹簧单元，分别代表沿连接面法向、纵向切向和横向切向的相互作用。每一个弹簧的长度设为0，其性能由上述粘结滑移本构关系转化成F～D曲线确定。

2.2模型网格划分处理

采取自上而下的建模方式，即先建立体单元，再自动生成与体单元相关的面单元、线单元和节点单元。建模时将型钢和混凝土都划分为规则的平行六面体单元，并保证划分后两者的节点坐标要一一对应，这样有利于在接触面上设置非线性弹簧单元。

由于研究对象与混凝土相关，根据混凝土结构主要是其所含骨料颗粒的大小特性，宜将混凝土划分为20mm×20mm×50mm左右体积大小的有限元网格，这样在计算中不会引起较大的误差。在划分时还要注意接触面上网格尺寸的一致性，保证型钢和混凝土单元节点在整体坐标系上一一对应。如图3所示。

图3　混凝土及型钢划分示意图

纵筋及箍筋划分时需依照保护层厚度确定好钢筋所在位置的节点，利用模型良好的规整性采用ANSYS程序建模菜单生成单元指令中的 Offset nodes指令生成钢筋单元，该方法通过控制节点在X、Y、Z三个方向的距离寻找节点对，并在满足条件的每一个节点对之间形成单元，如图4所示。

图4　钢筋节点及单元示意图

2.3模型加载及求解设置

加载时在型钢混凝土柱下端对X、Y、Z三个方向的位移和转动施加约束，形成刚接。在上端即施加荷载端除保留Z方向（在本文模拟中即型钢混凝土柱高度方向）位移外，约束其他各方向的位移和转动。约束条件可以保证在模拟分析时的受力情况与实验室完全一致，在进行加载时不会因为构件约束端发生偏移或转动引起分析错误，从而确保模拟分析的正确性。

模型求解过程中采用完全的牛顿—拉普森平衡迭代方法，并且选择稀疏矩阵求解器求解，计算过程中为提高模型计算时间，顺利实现收敛可以将二分法打开，选择大变形及预应力选项，使用线性搜索和预测，同时适当增加荷载子步数以及迭代次数，经笔者验证以上措施对模型精度没有影响，但对于节省计算时间，加快收敛，效果明显。

2.4型钢混凝土柱承压模型验证

本文在进行型钢混凝土柱受压性能有限元模拟分析时，采用试验数据［6］对比验证所建立模型的正确性以及结果分析的可靠性。为保证与参考文献试验的一致性，建模过程中所有参数均取自文献资料。

验证模型时选取二组试件，试件截面均为200mm×200mm，试件1高度为1400mm，试件2高度为1800mm。其他各项参数详见表2：

表2　对比试件参数表

模拟计算结果显示在承受轴压荷载作用下型钢混凝土柱构件的破坏阶段和破坏规律与试验结果有较大的吻合性，当荷载加到极限荷载80%时，在柱的中部出现纵向微裂缝，压缩变形增量大于荷载增量。当荷载进一步增大，主裂缝宽度增大，纵向裂缝贯通，纵筋和型钢开始屈曲。总体而言，无论是裂缝出现的位置、裂缝发展的过程以及破坏时裂缝所处的状态都与我们了解到的试验过程中所描述的现象相对应。

此外，模拟试件的受力特性与试验保持一致。在最后破坏时，中间单元混凝土应力达到28.44MPa，加载端混凝土单元应力达到32.47MPa，均已超过混凝土自身的强度极限，型钢单元的应力接近235MPa但未进入屈服阶段。型钢应力以及构件整体应力分布如图5所示。

图5　型钢及构件整体应力分布图

对比试验二组构件的最终承载力，通过ANSYS模拟得到的计算结果符合精度要求。具体数值见表3：

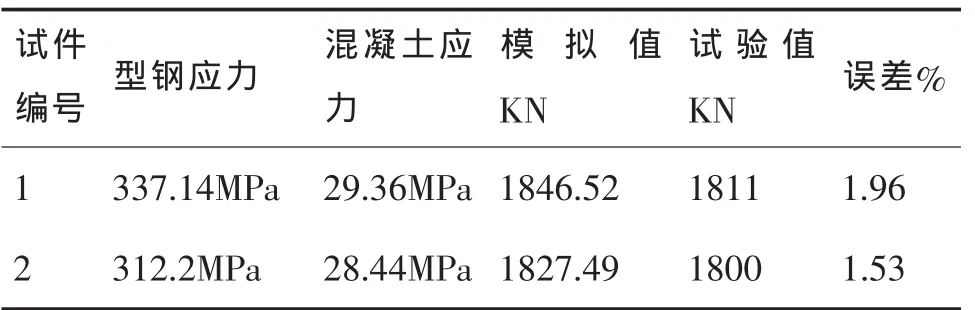
表3　数值模拟计算结果与试验数据对比表

综合两方面的数据比对，我们可以看出采用有限元数值模拟的方法对型钢混凝土柱的受力性能进行研究是可行的，在模型建立准确合理的情况下，分析所得数据具有相当的可靠性，各项误差均在允许范围之内。

3　型钢混凝土柱承压性能分析

对于型钢混凝土承压柱，影响其承压性能的主要因素有混凝土强度、配筋率及含刚率等，本节通过ANSYS进行来了大量模拟试验，得到了上述因素对型钢混凝土刚度，延性及承载力的影响规律。

3.1配筋率对型钢混凝土柱承压性能的影响

本组模拟数据主要分析不同的配筋率对型钢混凝土柱承压性能的影响。一共设置四个试件，试件模型截面尺寸为 200×200（mm），保护层厚度取30mm，混凝土强度等级均为C30，弹性模量为3.0× 104MPa，纵筋分别采用4φ8～4φ20不等，内含工字钢采用I10，箍筋采用φ6.5@100，配筋率设置从0.503%～3.14%不等。

图6　配筋率不同时柱承载力与柱端位移曲线

从图6可以看出，当混凝土强度等级、含钢率、配箍率等参数相同的情况下，配筋率的改变对型钢混凝土承载力有一定影响作用，四组模拟试件经计算分析后最终极限承载力最小值为1640.32KN，最大值为1955.21KN，最大极差值为314.89KN，差值约占平均值的比例为15.5%左右。随着配筋率的提高，构件在整体屈服前刚度基本没有差别，但在屈服后配筋率较大的构件刚度略有增加。由于施加荷载端的型钢和混凝土接触面粘结滑移破坏，承载力接近900KN时构件发生了一次应力重分布。最终破坏时型钢柱柱端位移值平均达到16.104mm，配筋率越高位移值相对较大，说明在合理的配筋率范围之内，配筋率的提高对改善构件的延性有一定的影响。

图7　柱承载性能随配筋率变化曲线

图7给出了配筋率变化时型钢混凝土轴压柱粘结破坏荷载、屈服承载力和极限承载力的变化情况。随着配筋率的提高，柱端粘结破坏荷载没有太大变化在900KN左右，配筋率的改变对粘结破坏荷载基本没有影响。构件的屈服承载力有所提高，最大相差值达到195.4KN，说明配筋率改变对屈服承载力有较明显的影响。同样，构件的极限承载能力随配筋率的提高而提高，提高幅度占极限承载能力的15%左右。表4给出了具体的承载能力变化值。

表4　配筋率不同时型钢混凝土柱的各项承载能力统计表

3.2混凝土强度对型钢混凝土柱承压性能的影响

本组模拟对比数据主要分析了不同的混凝土强度等级对型钢混凝土柱承压性能的影响。一共建立了四个试件模型，每个模型截面尺寸均为200× 200（mm），保护层厚度取30mm，纵筋均采用4φ12，配筋率为1.13%；内含工字钢统一采用I10；箍筋采用的是φ6.5，间距100mm，配箍率为0.33%；混凝土强度等级采用C30～C60不等，弹性模量设置为3.0× 104MPa～3.8×104MPa

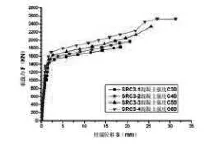
图8　混凝土强度不同时柱承载力与柱端位移曲线

图9　柱承载性能随混凝土强度等级变化曲线

从图8可以看出，随着混凝土强度的提高，型钢柱构件在整体屈服前，刚度有所增加；随着构件进入屈服，截面极限应力及构件刚度随混凝土强度提高而有所增长，表明混凝土强度对型钢柱屈服后刚度具有一定的影响作用。另外混凝土强度等级的变化，使构件在柱端发生应力重分布即产生粘结破坏时的承载力也相应有所变化。混凝土强度等级对构件粘结滑移性能的影响非常明显。

最终破坏时模拟构件柱端位移值差别比较大，试件SRC-3-1的柱端位移为18.46mm，而试件SRC-3-4的柱端位移接近31.3mm，表明强度等级的提高在增加构件承载力的同时对构件屈服后的延性有相当大改善作用。

图9给出了混凝土强度等级变化时型钢混凝土轴压柱三个特征阶段的承载力曲线。可以看出，混凝土强度等级对型钢柱承载力的影响十分明显。强度等级较高的试件，发生粘结破坏时达到的荷载水平也较高。说明高强度的混凝土不仅对提高构件自身的承载力有影响，对改善构件中组合截面的粘结性能也具有一定的影响作用。总体来看，型钢混凝土柱的屈服承载能力和极限承载能力随混凝土强度等级的提高而提高。见表5。

表5　混凝土强度等级不同时型钢混凝土柱的各项承载能力统计表

3.3含钢量对型钢混凝土柱承压性能的影响

本组模拟对比数据主要分析不同的型钢混凝土柱含钢率对柱体受压性能的影响。一共设置了六个试件，型钢混凝土柱截面尺寸为200×200（mm），保护层厚度近似取30mm，混凝土强度等级均为C40，弹性模量为3.25×104MPa，纵筋采用4φ12，配筋率为1.13%，箍筋采用φ6.5@100，配箍率为0.33%，内含工字钢采用不同的截面尺寸，含钢率设置为3.39%～9.16%不等。

图10　含钢率不同时柱承载力与柱端位移曲线

图10表明，随着含钢率的提高，型钢混凝土柱在受压屈服前后，刚度基本没有太大变化；但随着含钢率的提高构件承载能力得到了显著的改善。含钢率是构件承载能力最主要的影响因素。

最终破坏时柱端位移值差别不大，试件SRC-4-1的柱端位移为16.8mm，而试件SRC-4-6的柱端位移仅为20.6mm，表明含钢率的提高对增加构件承载力的作用要远大于改善构件延性的作用。

图11　柱承载性能随含钢率变化曲线

图11给出了含钢率变化时型钢混凝土轴压柱三个特征阶段的承载力曲线。可以看出，在低含钢率范围内，随含钢率的提高构件粘结破坏荷载、屈服承载力和极限承载力均有所提高，但当含钢率接近8%时，提高幅度开始减小，曲线相对较为平缓，含钢率变化对特征承载力的影响减弱。表明含钢率对构件承载力的影响存在界限效应，在设计中要合理设置型钢混凝土柱的含钢率，过低及过高的含钢率都不可取。见表6。

4　结论

针对混凝土强度等级、配筋率以及含钢率这三个因素的变化进行了大量数值模拟试验，对型钢混凝土柱承压性能（刚度、延性及承载力）的影响规律，进行了分析和对比：可以看出，混凝土强度的变化，对构件加载前、后期的刚度均有影响，而含钢率的增大对柱加载前期的刚度有提高作用；对于构件的承载力，在合理范围内，含钢率的提高可以大大的增加柱的承载能力，是影响构件极限承载力最主要的因素。混凝土强度等级对承载力的影响仅次于含钢率，配筋率的提高在加载后期对柱承载力有一定贡献，但程度不大。对于构件的延性，混凝土强度和配筋率的提高对构件延性均有一定程度上的改善作用，影响程度相差不大，而含钢率对构件延性基本没有影响。

此外，通过对模拟试验组的分析可知，在加载后期，加载端型钢与混凝土之间均存在不同程度的粘结破坏现象，导致型钢与混凝土之间出现应力重分布。型钢与混凝土接触面粘结滑移现象的存在对型钢混凝土柱后期承压性能以及变形协调能力有较大的影响。