激波诱导模型球阵非稳态阻力的数值模拟研究

郝李娜，章利特，王天航，施红辉

(浙江理工大学机械与自动控制学院，杭州 310018)



激波诱导模型球阵非稳态阻力的数值模拟研究

郝李娜，章利特，王天航，施红辉

(浙江理工大学机械与自动控制学院，杭州 310018)

采用CFD软件，对激波诱导单排四球模型球阵绕流场进行三维数值模拟，在计算模型和方法准确性验证基础上，分析模型球非稳态阻力的形成机理，并揭示激波马赫数Ms和无量纲间距H对非稳态阻力和激波结构的影响。结果表明：模型球阻力系数Cd曲线存在一个尖锐的最大值波峰和一个波谷的结构，且最终趋于某一稳态正值；Ms越小，Cd峰值越大，谷值越小，Cd曲线波动幅度越大；激波反射、衍射、聚焦和干涉行为共同影响非稳态阻力系数；无量纲间距H越小，相邻球的激波干涉越显著，Cd峰值越大。

激波；模型球阵；非稳态阻力；阻力系数；激波干涉

0　引　言

激波与固体颗粒群相互作用的现象普遍存在于自然界和工业生产中，对该现象的研究一直是超声速气-固两相流领域的重要课题之一。目前，国内外研究学者已针对激波管内可压缩性气-固两相流的现象，采用实验和数值模拟等手段进行了一系列研究。Sun等[1]对平面激波加载单模型球时的非稳态阻力进行了实验测量，发现在模型球直径或雷诺数较大的情况下，非稳态阻力会较大。Saito等[2]通过对含激波的气体-颗粒混合物两相流动进行数值模拟，研究了不稳定阻力对激波后非平衡流场结构的影响，发现在激波与颗粒群相互作用早期非稳态阻力对流动结构的影响较大。Igra等[3]对激波诱导的单颗粒绕流场进行了数值模拟后得出，作用在小球上的阻力主要取决于球表面压力和粘性剪切应力分布以及尾迹湍流结构。施红辉等对激波与颗粒群相互作用时的反射、透射和衍射行为进行了实验研究[4-6]，发现激波的这些动力学行为导致了颗粒群阻力系数显著的非稳态性，表现为其具有明显的波峰、波谷结构。Shi等[7]对激波与模型球阵相互作用时的反射和聚集机理进行了实验研究，发现相邻球之间存在明显的激波干涉行为，认为颗粒群阻力系数建模时必须将其加以考虑。陈婉君等[8]对激波诱导的双圆柱绕流场和阻力系数进行了二维数值计算，发现了明显的双圆柱激波结构的干涉行为，这对圆柱面压力、剪切应力分布并最终对圆柱阻力产生显著的影响。Jourdan等[9]利用光学方法捕捉了单颗粒球的运动轨迹，并进行了颗粒运动参数的推导，据此研究激波驱动下颗粒的运动规律。Parmar等[10]利用插值方法得到了雷诺数、马赫数适用范围都很广且精度相当高的单球阻力系数经验公式，该公式可直接用于固体颗粒相为稀相时的气-固两相流建模。

上述研究主要关注激波与单球的相互作用，一些学者(如Parmar等[10])所建立的阻力系数模型在稀颗粒相气-固两相流中的适用性已经得到充分验证。从先前学者对激波与多球(圆柱)相互作用的研究中不难得出，邻近球(圆柱)的激波结构存在干涉行为，它势必会对颗粒阻力产生影响，但这方面的物理机理和规律研究仍不够全面深入。鉴于颗粒阻力在两相流相间耦合建模方面的重要性，有必要开展激波诱导球阵的绕流场及阻力的数值计算，探索颗粒群非稳态阻力形成机理和影响规律。为此，本文将介绍激波诱导球阵(单排四球)绕流场和阻力的计算模型与方法，并探讨激波马赫数Ms、无量纲间距H对非稳态阻力的影响。

1　三维计算模型与计算方法

1.1控制方程

激波诱导模型球阵绕流场属于三维非定常可压缩粘性流动，该流动可用Navier-Stokes方程描述。

连续性方程：

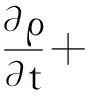
(1)

动量守恒方程：

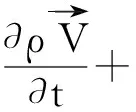
(2)

能量方程：

=-

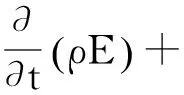
(3)

其中E表示单位质量总能，

(4)

(5)

1.2三维计算模型及计算参数

三维计算模型如图1所示，计算区域总尺寸为0.7m×0.2m×0.2m，其中波后气流区域尺寸为0.2m×0.2m×0.2m，模型球(阵)中心到计算区域入口端面距离为0.3m，模型球直径均为0.04m。计算区域的截面尺寸与实际测试段一致，但为了节约计算时间，同时又不影响模型球阵非稳态阻力的分析，球阵前后均只截取的部分长度，计算结果在入口或出口反射波到达球阵前有效。采用压力进口、压力出口和无滑移壁面(包括管和球壁面)条件。计算区域的网格划分采用了结构化网格，球的近壁面区域作了网格加密处理，网格总数约为90万。表1显示了根据激波管理论确定的流场计算参数，其中：p2、V2、T2、p0和T0分别表示波后气流的压力、速度、温度、滞止压力和滞止温度； p1和T1分别表示波前气流的压力和温度，分别取为实验条件下的平均值0.1013MPa和28 ℃。激波前、后气体均为空气。激波马赫数Ms定义为入射激波速度与被驱动初始声速(约为347.85m/s)之比，无量纲间距H定义为两相邻球球心间距L(如图7所示)与球直径D之比，Ms和H取值范围均来自于实验工况。

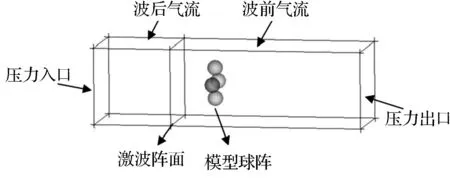
图1　单排四球模型球阵绕流场的计算区域

MsHV2/(m·s-1)ρ2/(kg·m-3)p2/PaT2/Kp0/PaT0/K1.06361.18091.26981.41061.6/1.8/2.035.81.298116840313.7117706314.3596.81.534147963336.1156147341.30139.81.715173717352.9194165364.30203.42.002218331379.9275205405.89

1.3非稳态阻力系数的计算

Igra等[3]通过对激波与单模型球相互作用的数值模拟发现，模型球所受的阻力主要由作用于其表面的流体粘性剪切力和压力共同决定，故本文进行了模型球表面压力和剪切应力的分析。图2中，Δσ为球表面任一局部小面积；γο为外法向单位矢量，其指向与球面压力Pγ方向相反；φo为球面纬线切向单位矢量，与纬线剪切力τφ同向；θο为球面经线切向单位矢量，与经线剪切力τθ同向；i是x轴方向单位矢量；j是y轴方向单位矢量；k是z轴方向单位矢量；θ为球心角，即为外法向单位矢量γο与z轴正向之间的夹角；φ为球面纬线切向单位矢量φo与x轴负向之间的夹角。

由于球阻力等于x方向的合外力，即球面压力Pγ、纬线剪切力τφ和经线剪切力τθ对应的力沿x轴投影的叠加，可建立非稳态阻力FD与球面压力和剪切应力的积分关系：

FD=∬

(6)

设球面小面积总数为N，可得到阻力FD的离散形式：

FD=

(7)

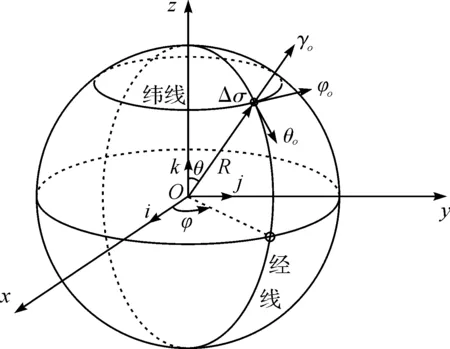
图2　球面压力与剪切应力分析图

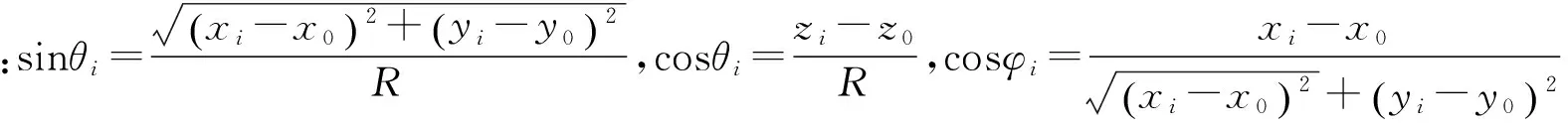
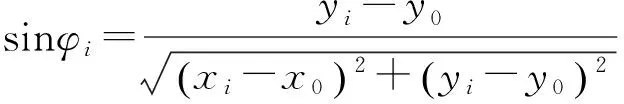
(8)

阻力系数定义为：

(9)

其中：ρ2和v2分别为波后气流密度和速度，π为圆周率，R为球半径。

1.4计算准确性验证

图3(a)和图(3)(b)分别显示了Ms=1.2698时，t=0和50 μs两个时刻激波管轴线上的压力和速度分布的计算结果，其中t=0对应了激波恰好到达球前驻点的时刻，激波阵面此时位于x=0.2 m处。根据图3(a)和图3(b)中的压力和速度间断位置可知，激波在50 μs内的传播距离为0.02215 m，故激波速度和马赫数的数值计算结果分别为443 m/s和1.2735。其中，数值计算的激波马赫数与理论值Ms=1.2698相比，相对误差仅为0.29%。

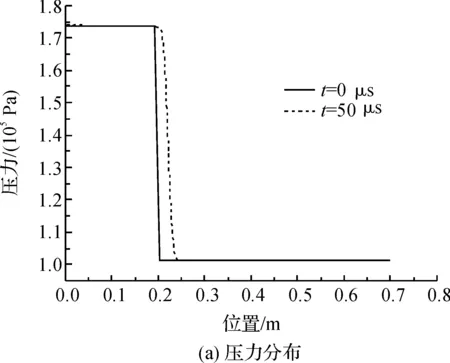
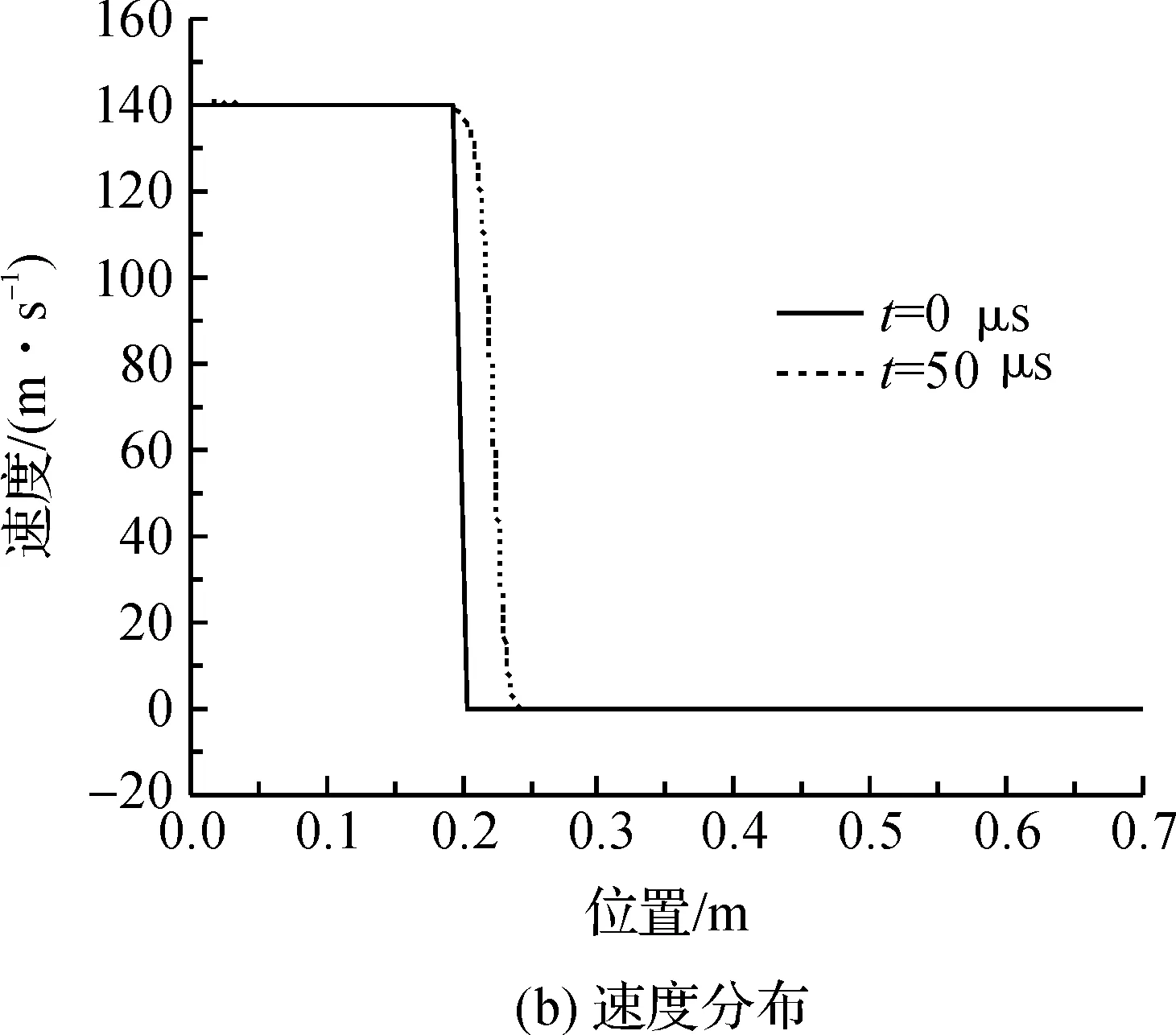
图3　沿激波管轴线的压力分布和速度分布

图4为Ms=1.2698时的Cd实验曲线和计算结果的比较，可以发现两条波形曲线具有极相似的变化规律，即Cd随着时间的增大，先出现一个尖锐的最大正值波峰，继而快速减小到一个负值波谷，之后上升回复到正值，最终趋于一个稳定正值。数值计算的Cd峰值为5.033，实验测量值为4.967，相对误差仅为1.03%。文中提及的实验Cd曲线和实验纹影图均由本文实验获得。由于实验采用的激波管装置内径较大，为200 mm装置，膜片的不规则破裂引起了尾随入射激波的小波结构，又由于此时激波马赫数较小，小波衍射和聚集长时间存在，这导致了Cd实验曲线在负值波谷之后出现较明显的小幅(相对于峰值)振荡阶段。然而在数值模拟中，采用了正激波间断关系，相当于采用了理想的规则破膜假设，即不存在上述小波结构，因此计算的Cd曲线在上述相应阶段未出现明显振荡。

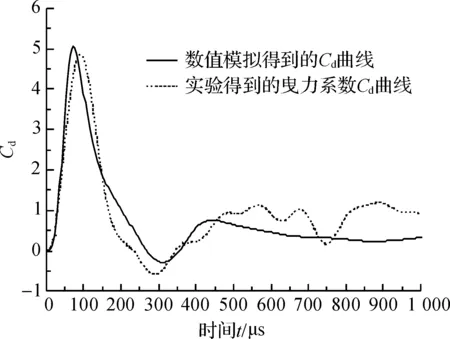
图4　Ms=1.2698时，单排四球模型Cd实验曲线和计算结果的比较

图5为Ms=1.2698时，不同时刻(图5 (a)t=20 μs、图5 (b)t=45 μs、图5 (c)t=90 μs数值计算的密度梯度图与实验纹影图的对比。由于实验纹影图视角垂直于激波管轴线，四球中距离观察者最近和最远的两球影像重叠地位于上、下两球的正中间处，因此实验图像显示为并列纵排的三球影像。而数值计算密度梯度图为激波管轴截面图，故其显示为并列纵排两球的影像。通过对比可以发现，数值计算跟纹影拍摄的透射和反射激波结构在不同时刻都很好地吻合。为定量比较起见，定义数值计算的密度梯度图(左半)和实验纹影图(右半)中球心到球面反射激波面前缘的距离分别为Xc和Xe(见图5 (b))，通过测量可以发现，在t=45 μs时刻，前后两者之间的相对误差仅为2.6%。

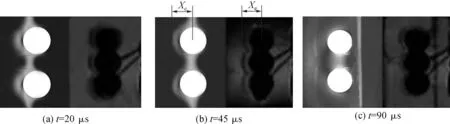
图5　Ms=1.2698时单排四球模型密度梯度数值模拟图(左半)与实验纹影图(右半)的对比

以上分别从流场参数、模型球阻力系数和激波结构三方面，进行了数值模拟结果与实验数据(或激波管理论值)的对比，充分验证了本文数值计算模型和方法的准确性。

2　数值模拟结果及分析

2.1阻力系数Cd与时间t的关系

图6显示了H=1.6时，不同Ms下模型球阻力系数Cd与时间t的关系。从图6中可以发现，不同Ms下阻力系数曲线的变化趋势基本一致，即：随着t的增大，Cd曲线先急剧上升，出现一个最大正值波峰后急速减小，出现一个波谷，继而渐进趋于一个稳定值，严格来讲，最终趋于一个稳态阶段的正值。且Ms越小，Cd峰值越大，谷值越小，波动幅度越大，Cd越难趋于稳定。由图6中最小激波马赫数Ms=1.0636时的Cd曲线可以发现，在1000μs计算时间内，Cd仍未回复正值，但通过更长时间(约2000μs)的计算可以发现，Cd最终可以回复正值，见图9。Ms对Cd产生上述影响的原因是，强度较弱的激波在球赤道后的衍射和球后驻点附近区域的聚集行为会持续更长时间，从而使Cd的非稳态阶段维持的时间更长。

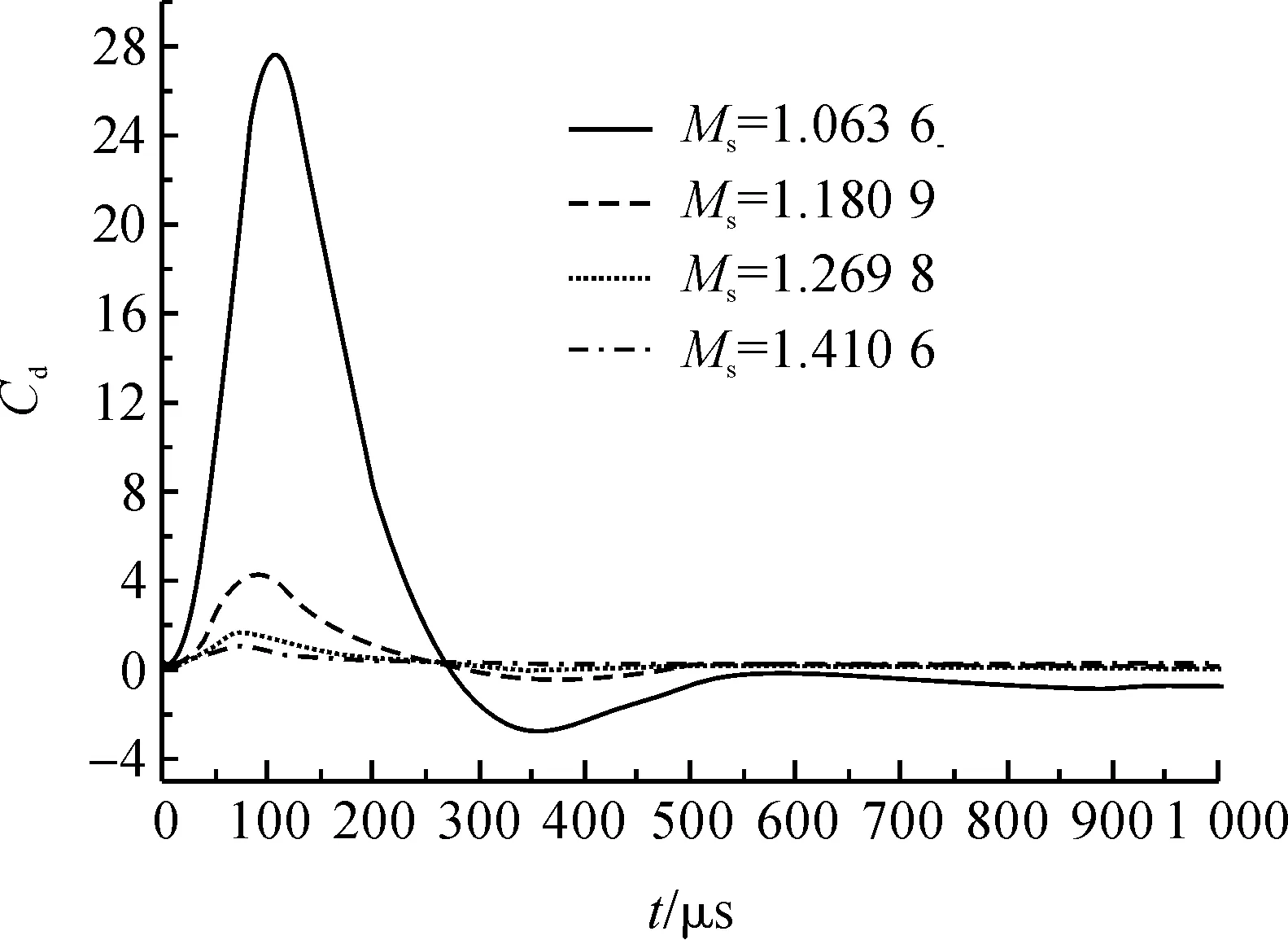
图6　不同激波马赫数下单排四球模型阻力系数与时间的关系曲线

2.2阻力系数Cd与压力云图的同步比对

为了深入研究不同球之间激波结构相互干涉的影响，取间距较小的相邻两球为观测对象，并选取如图7所示的球阵斜截面为压力云图提取截面。图8为激波马赫数Ms=1.1809时，不同时刻球轴截面外半圆周上的压力和剪切应力分布，此处外半圆周指相对两球(见图7中的上、下两球)轴截面外侧半圆周线，可以看出，在本文关注的激波与球阵相互作用期间，压力比剪切应力值大4～5个量级，这说明该阶段阻力FD取决于球周围压力分布，而受球面剪切应力影响极小，完全可以忽略不计，因此本文只进行压力云图与阻力系数Cd曲线的同步对比。

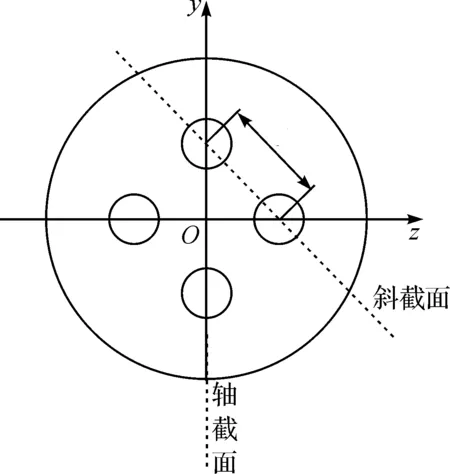
图7　单排四球模型球阵数据提取截面示意

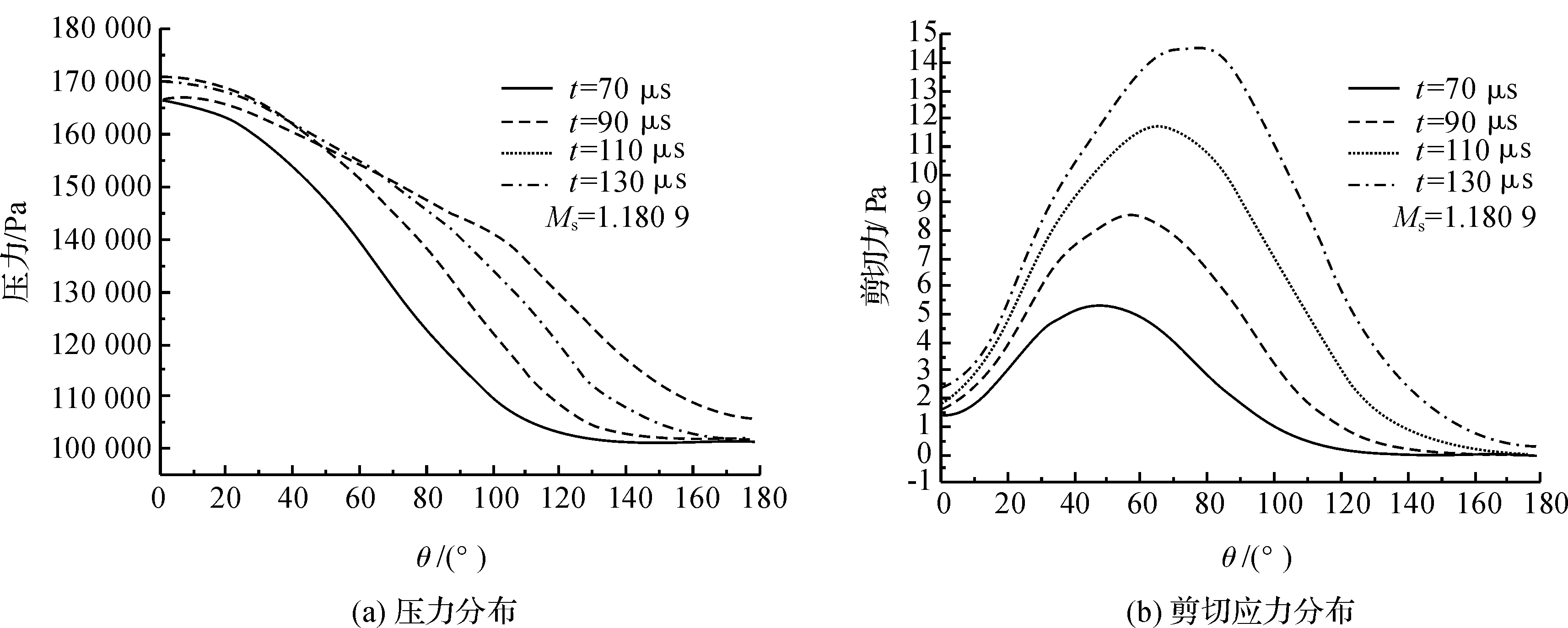
图8　不同时刻球轴截面外半圆周上的压力和剪切应力分布

图9和图10分别为Ms=1.1809时模型球Cd曲线和对应于图9中各标注时刻球阵斜截面上的压力云图。由图10可以发现，激波阵面后的压力呈条带状分布，而并非预期的大片区域均匀分布，这可能是以下两方面原因造成的：一是数值模拟时考虑了流体粘性的影响，二是所采用的二阶迎风差分格式对激波阵面的分辨能力有限。通过更细地时间同步对比可发现：在a时刻，入射激波还未到达模型球前驻点，球面压力依然保持初始状态(见图10(a))，阻力系数为0；在b时刻，入射激波开始与模型球相互作用，在小球前驻点附近开始出现高压区(见图10(b))，阻力系数由0增大到2左右；在c时刻，入射激波到达模型球赤道附近，球面反射激波发生干涉，两个球的高压区域相交(见图10(b))，阻力值急剧增大到峰值；在d、e时刻，激波继续向下游移动并发生衍射，赤道下游球面激波投射区域扩大，同时赤道上游半球的高压区域向外扩大、压力下降(见图10(d)和(e))，阻力下降；在f时刻，入射激波波前已远离后驻点，处于图10压力云图视野范围之外，球面反射激波已远离赤道上游球面，之前由于球面反射造成的激波后高压区已消失，另一方面，由于衍射激波在后驻点附近的持续聚集，该处变为高压区(见图10(f))，从而导致阻力最小值的出现；在g时刻，在前驻点附近发生激波的二次反射，使得该处又出现高压区域，此时衍射波在后驻点近区的聚集行为已经结束，该处的高压区也已完全消失(见图10(g))，导致了阻力第二峰值的出现。

图9　H=1.6，Ms=1.1809时的Cd曲线

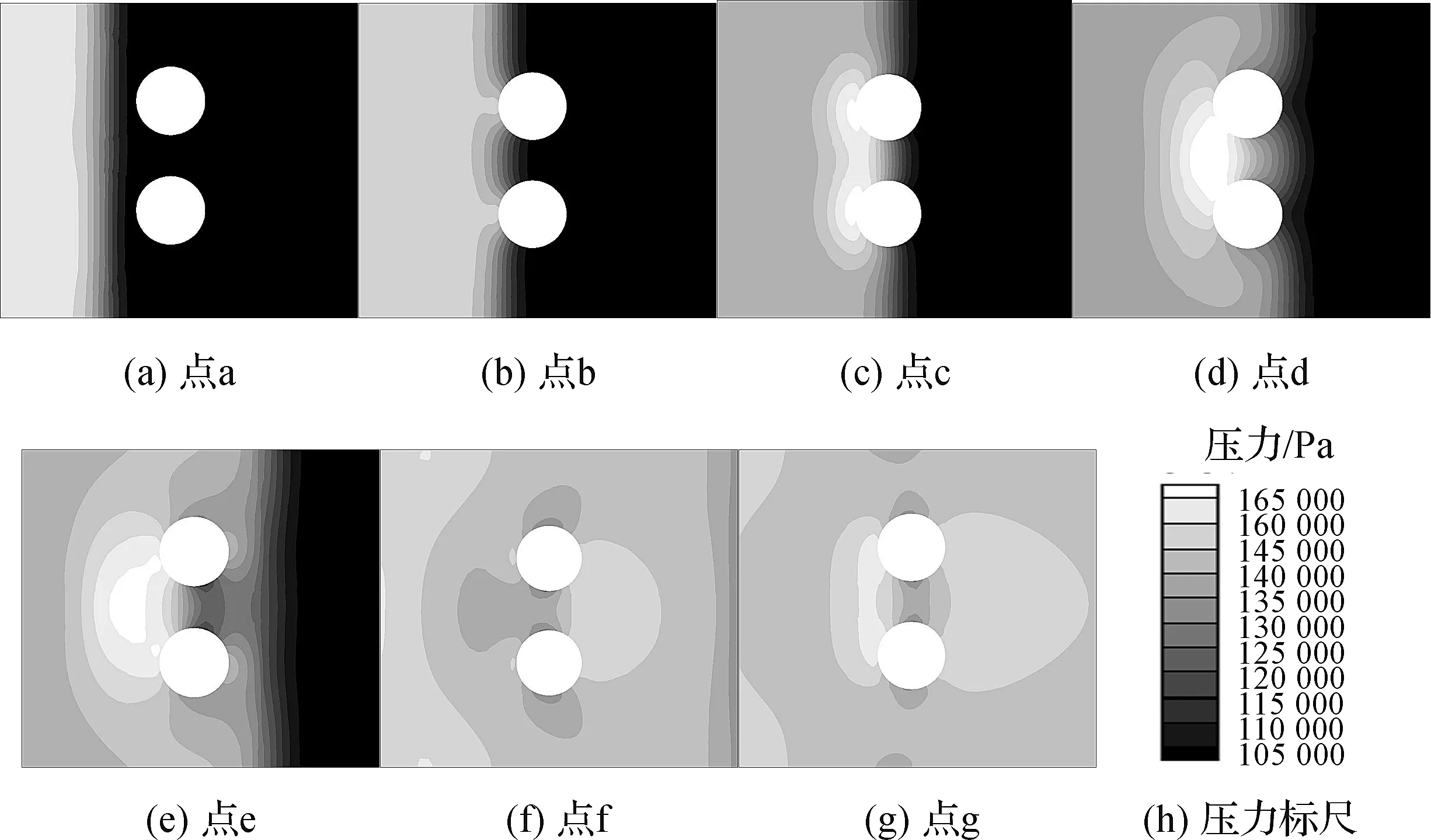
图10　对应于图9中各标注时刻球阵斜截面上的压力云图

2.3球面压力分布曲线

图11显示了不同激波马赫数Ms下Cd曲线代表时刻球轴截面外半圆周上的压力分布，其中0°、90°和180°分别对应了模型球的前驻点、赤道线和后驻点位置。图11(a)为不同Ms下Cd波峰时刻球轴截面外半圆周上的压力分布，从图11中可以看出，在Cd波峰时刻，前驻点处压力值最大，压力值随位置的后移持续减小，在球后驻点前某处达到最小值，即初始压力101325 Pa，且Ms越大，球面上分布的压力值越大。由图11(b)可以看出，Cd波谷时刻，球面分布的压力值随位置的后移，先减小后增大，压力最小值出现在约100°位置，且Ms越大，压力变化越剧烈，前、后驻点处的压力差值越大。由图11(c)可以看出，Cd第二波峰时刻，前驻点处压力值最大，但该值显著小于Cd波峰时刻的相应值，球面压力随角度增大，先减后增，在后驻点附近可能再次减小，压力最小值出现在约80°位置处，且Ms越大，压力变化越剧烈。

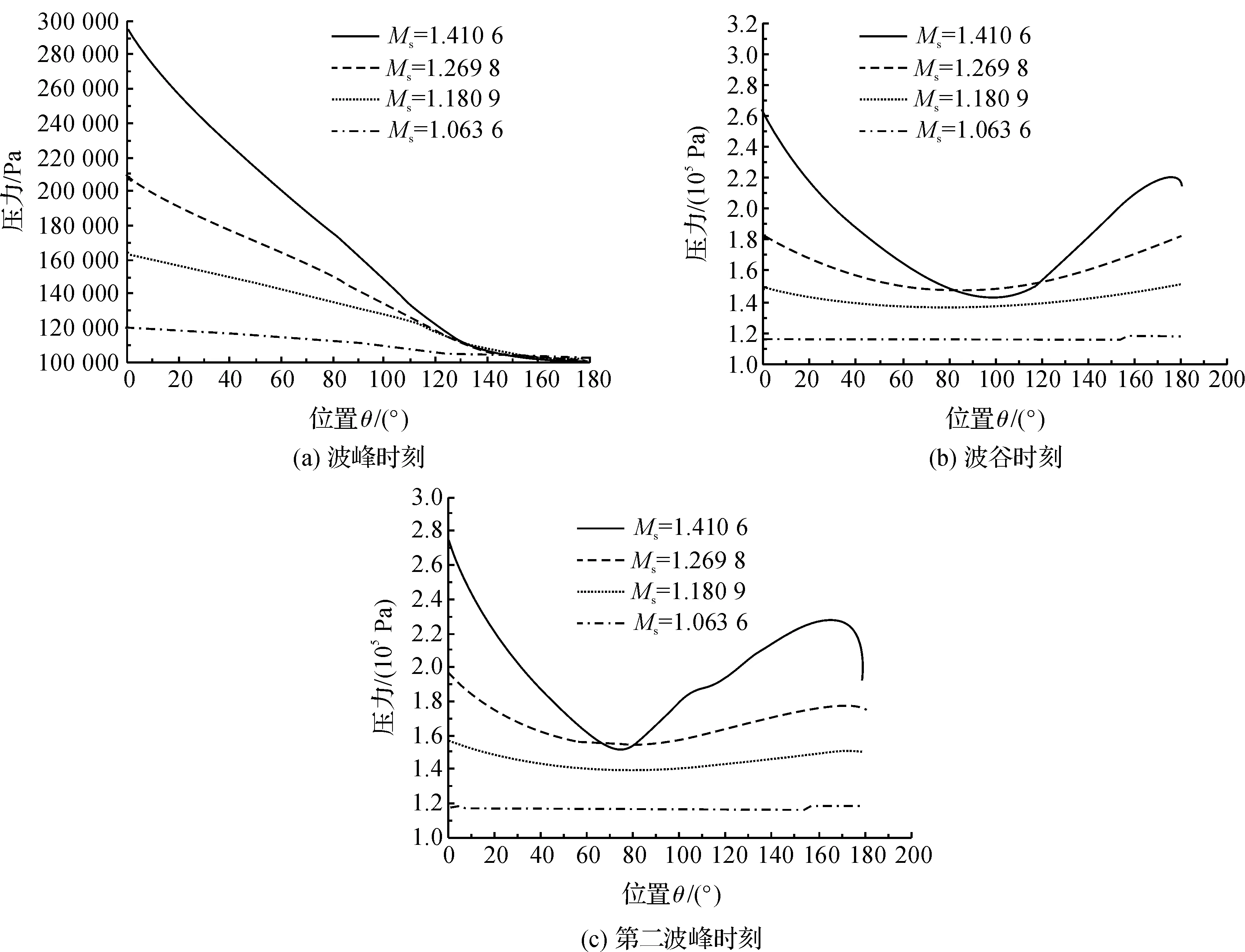
图11　不同Ms下，Cd曲线代表时刻球轴截面外半圆周上的压力分布

2.4H对激波干涉和Cd峰值的影响

图12为激波马赫数Ms= 1.2698时，不同无量纲间距H下Cd峰值时刻球轴截面外半圆周上的压力分布，可以发现，此时入射激波前缘均到达赤道面附近，无法分辨位置差异，无量纲间距H=1.6和H=1.8时反射激波在双球内侧发生明显的干涉行为，表现为双球反射激波阵面的交汇和波后高压区的合并，且H=1.6时上述现象相对更为显著，其结果是对双球内侧压力分布乃至球的阻力影响更大，而当H=2.0时，未见明显的双球反射激波干涉行为。综上可得出，相邻球无量纲间距越小，反射激波干涉越显著，进而对球阻力的影响越大。

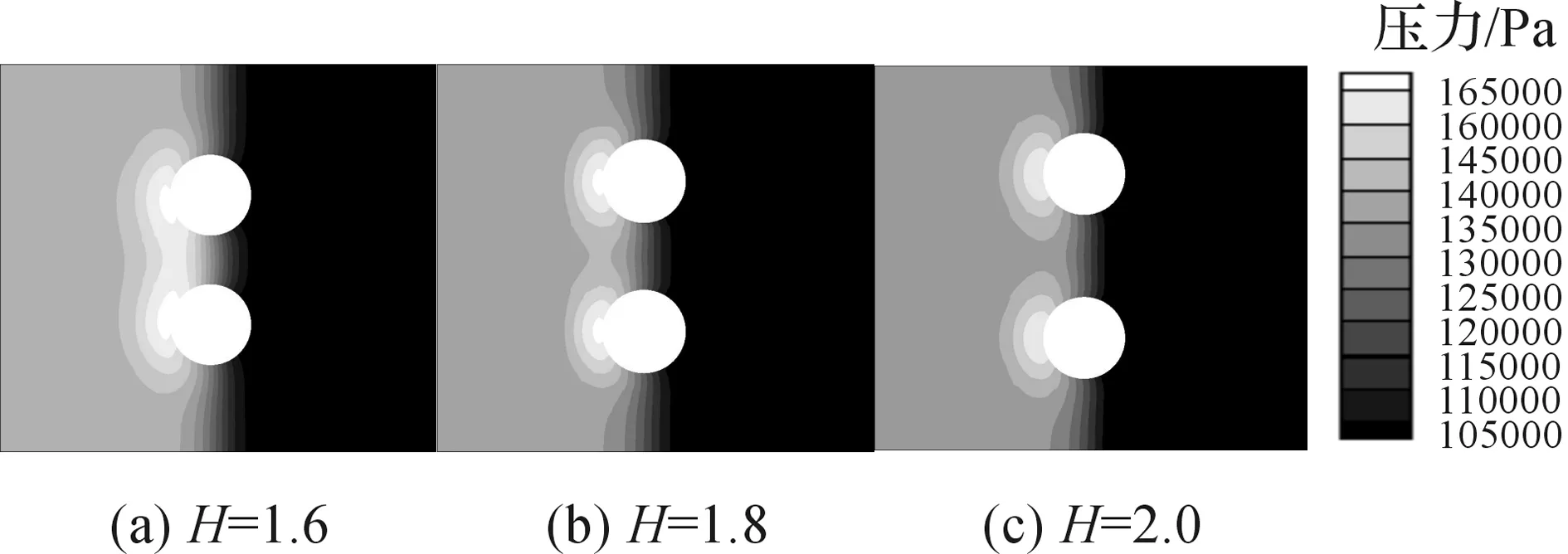
图12　Ms= 1.2698时，不同H下Cd峰值时刻球轴截面外半圆周上的压力分布

图13为Ms=1.2698时，不同无量纲间距下的曳力系数Cd曲线。发现随着H的减小，由于激波间的干涉行为逐渐变得更加剧烈，Cd峰值增大，在出现第二峰值之后，Cd曲线渐渐平稳，并趋近于一个稳定的正值。

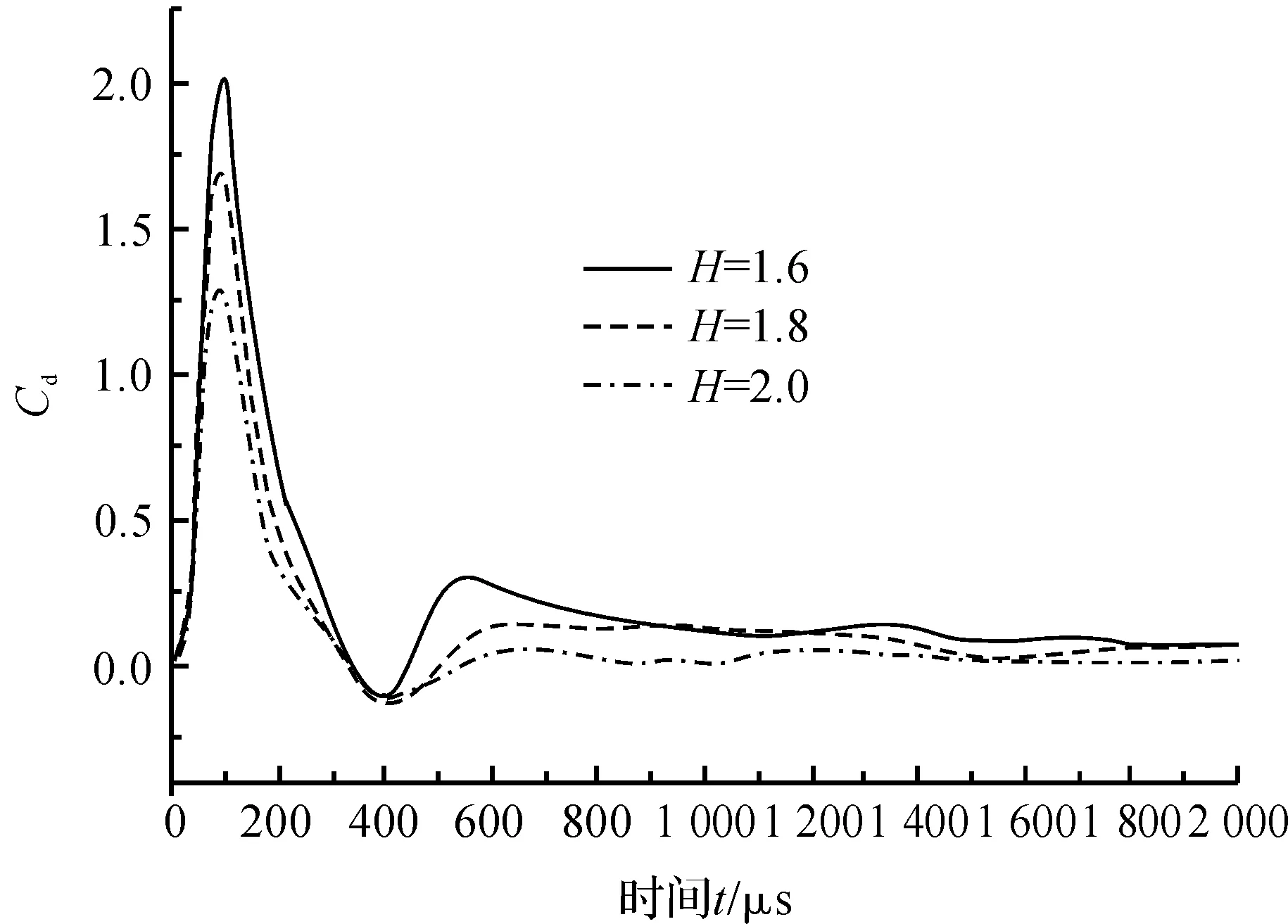
图13　Ms= 1.2698时不同H下的Cd曲线

3　结　论

本文进行了单排四球球阵在激波作用下的绕流场和非稳态阻力的数值计算和分析，主要结论如下：

a)模型球阻力系数Cd曲线先后出现一个尖锐的最大值波峰和最小值波谷，激波马赫数Ms较小时可能出现负的Cd谷值，随后逐渐回复并最终趋于某一稳态正值。

b)Ms越小，Cd峰值越大，谷值越小，Cd曲线波动幅度越大，需要更长时间趋于稳态。

c)激波与球阵相互作用的过程中，出现的激波反射、衍射、聚焦和干涉行为共同影响球面的压力分布，进而影响非稳态阻力(系数)。

d)无量纲间距H会影响球面反射激波的干涉行为，从而改变球面压力分布，进而导致Cd曲线的差异；H越小，激波干涉越显著，Cd峰值越大。

[1]SUNM,SAITOT,TAKAYAMAK,etal.Unsteadydragonaspherebyshockwaveloading[J].ShockWaves,2005,14(1/2):3-9.

[2]SAITOT,SABAM,SUNM,etal.Theeffectofanunsteadydragforceonthestructureofanon-equilibriumregionbehindashockwaveinagas-particlemixture[J].ShockWaves,2007,17(4):255-262.

[3]IGRAD,IGRAO,HOUASL,etal.Simulationofsphere’smotioninducedbyshockwaves[J].JournalofFluidsEngineering,2012,134(10):21-24.

[4]ZHANGLT,SHIHH,WANGC,etal.Aerodynamiccharacteristicsofsolidparticles’accelerationbyshockwaves[J].ShockWaves,2011,21(3):243-252.

[5] 章利特,施红辉,王超,等.激波与可运动颗粒群相互作用反射与透射机理实验研究[J].应用力学学报,2010,27(2):280-285.

[6] 张晓娜,岳树元,章利特,等.激波驱动的气固两相流力学特性研究[J].水动力学研究与进展:A辑,2008,23(5):538-545.

[7]SHIHH,YAMAMURAK.Theinteractionbetweenshockwavesandsolidspheresarraysinashocktube[J].ActaMechanicaSinica,2004,20(3):219-227.

[8] 陈婉君,章利特,施红辉,等.激波加载单双圆柱非稳态曳力的数值研究[J].浙江理工大学学报,2015,30(2):208-212.

[9]JOURDANG,HOUASL,IGRAO,etal.Shocktubestudyofthedragcoefficientofasphere[J].ShockWaves,2009,7:521-526.

[10]PARMARM,HASELBACHERA,BALACHANDARS.Improveddragcorrelationforspheresandapplicationtoshock-tubeexperiments[J].AIAAJournal,2010,48(6):1273-1276.

(责任编辑： 康锋)

Numerical Simulation Study on Unsteady Drag Force Acting on Model-Sphere Array Induced by Shock Wave

HAOLina,ZHANGLite,WANGTianhang,SHIHonghui

(Faculty of Mechanical Engineering & Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China)

In this study, the 3D numerical simulation of a gas flow around a four-spheres-in-one-row array induced by shock wave was performed with CFD software. Based on verifying the accuracy of calculation model and method, the formation mechanism of unsteady drag force exerted on a model sphere and the effect of the Mach numberMsof shock wave and the non-dimensional interval distanceHon unsteady drag force and shock wave structure were analyzed. The result shows that each curve of the drag coefficientCdhas a sharp maximum value peak and a valley, and finallyCdtends to be a steady-state positive value. Furthermore, the smaller the value ofMsis, the larger the peak value and the fluctuating amplitude of the curve, and the smaller the valley value ofCd. Besides, the combination of shock wave reflection, diffraction, focusing and interference behaviors affects the unsteady drag coefficient. And the smaller the value ofHis, the more remarkable the shock interference between adjacent spheres, and the larger the peak value ofCd.

shock wave; model-sphere array; unsteady drag force; drag coefficient; shock wave interference

10.3969/j.issn.1673-3851.2016.09.0016

2015-11-16

国家自然科学基金项目(51006091)；浙江省自然科学基金项目(LY13E060011)；流体机械及工程省重点学科及流体工程技术创新团队项目(11130031201301)；流动腐蚀与防控技术创新团队(浙理工科〔2013〕13号)

郝李娜(1990-)，女，山西太原人，硕士研究生，主要从事湍流与复杂流动以及可压缩性与瞬态流动方面的研究。

章利特，E-mail: langzichsh@zstu.edu.cn

TK121

A

1673- 3851 (2016) 05- 0726- 08 引用页码： 090403