2-SPR-RPS并联机构静力分析

张宁斌，项济南，李秦川，陈巧红

(浙江理工大学，a.机械与自动控制学院；b.信息学院，杭州 310018)



2-SPR-RPS并联机构静力分析

张宁斌a，项济南a，李秦川a，陈巧红b

(浙江理工大学，a.机械与自动控制学院；b.信息学院，杭州 310018)

2-SPR-RPS并联机构具有1个移动和2个转动自由度，可用做搅拌摩擦焊机器人。在实际工况下，该机构端部动平台受力条件复杂，多支链耦合，故有必要对其进行静力学分析。首先通过拆杆，建立矢量6维力平衡方程；其次采用自由度解耦，分别调整动平台2个转角和动平台高度值，分析了3种单自由度状态下各杆件受力曲线，从而获得输出端位姿参数与并联机构驱动-约束反力之间的映射；最后，对单变量参数重新组合，得到完整的静力图谱。研究结果可对2-SPR-RPS并联机构的驱动电机选型、机构关节承载分析、结构强度设计提供参考。

并联机构；少自由度；静力分析；矢量法

0　引　言

并联机器人是机器人的一大分支，与串联机器人相比，具有累积误差小、承载能力大、刚度好、惯性力较小等优点，因而在某些应用上有很大优势。少自由度并联机构[1]的自由度少于6，结构简约，驱动件少，控制简便，成本相对低廉，具有广阔的工业应用前景[2-4]。

机构静力传递特性分析[5-7]是设计少自由度并联机构的重要环节。静力分析能够初步确定机器工作时所需的驱动力、约束反力、能承受的最大载荷等，为动力学分析、机构整体结构设计、驱动器设计、强度校核等提供依据。

国内外学者已对少自由度并联机构的静力分析进行了研究。刚度映射是早期研究并联机构内部静力传递特性的主要方法[8]，而对于轻型机构而言，重力产生主动力较小，故在实际平衡计算中将其忽略[9]。在此基础之上，赵燕等[10-11]对含有过约束力偶的少自由度并联机构进行了主动力和约束力分析。现代数学理论的引入丰富了并联机构静力性能的分析方法，如：李永刚等[12]以微分流形理论为基础，指出了少自由度并联机构末端的力空间，从而对此类机构驱动力与约束力的传递特性进行了分析；高峰等[13]对一种5维并联机构，采用了一种新型解耦方法来研究其力传递的各向同性；Lu[14]运用虚功原理和CAD几何变量法分析了空间并联机构的主动力和被动力。

具有1个移动和2个转动自由度的2-SPR-RPS并联机构可作为搅拌摩擦焊工作台。在焊接过程中，工作台主轴方向上受到极大的轴向力，而各分支传递到工作台上的6维力耦合，故有必要对整个机构受力情况进行分析。对于少自由度并联机构，仅研究支链驱动力不足以描述机构整体受力特征，其完整的末端力空间应包括驱动力和约束力子空间[5]。将2-SPR-RPS并联机构各杆件进行拆分，可建立各部分6维力平衡方程。按照机构自由度对动平台运动解耦，通过调整动平台参数，分析3种单自由度状态下机构受力曲线，可获得各运动参数对并联机构所需驱动力和各运动副约束反力分布的影响特征。静力分析结果可对2-SPR-RPS并联机构的大功率驱动电机选型、机构关节承载、结构强度设计提供数据支持。

1　自由度分析

2-SPR-RPS机构由动平台、固定平台以及连接两平台的三条分支构成，如图1所示。其中第1、2分支均为SPR分支，第3分支为RPS分支(S代表球副，P代表移动副，R代表转动副)。3个分支驱动副均为移动副，力作用点为bi。基座为等腰直角三角形△A1A2A3，满足OA1=OA2=OA3=r1，固定坐标系O-XYZ，记为{O}，原点为斜边A1A2中点，x轴沿OA2方向，y轴沿OA3方向，z轴根据右手理论建立。动平台为等腰直角三角形△B1B2B3，满足oB1=oB2=oB3=r2，动坐标系o-xyz，记为{o}，建立在斜边B1B2中点，x轴沿oB2方向，y轴沿oB3方向，z轴根据右手理论建立。过A3点的转动副轴线平行A1A2所在直线；过B1、B2点的转动副轴线均平行于oB3所在直线。

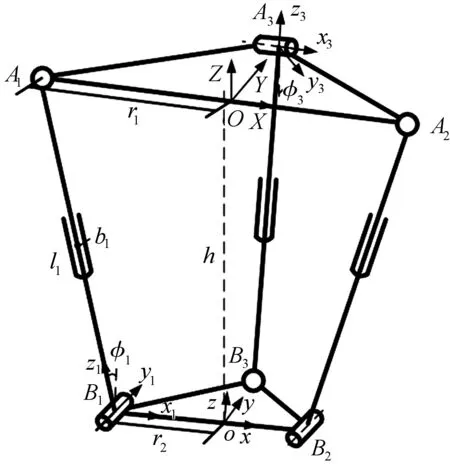
图1　2-SPR-RPS并联机构示意

基于螺旋理论修正的Grübler-Kutzbach公式[1]，可得机构自由度M：

(1)

其中：d—机构公共约束；n—机构构件个数；g—机构运动副数；fi—机构第i个运动副的自由度数；v—机构冗余约束数。则并联机构2-SPR-RPS自由度为：M=6×(8-9-1)+15+0=3。3个自由度分别为：沿Z轴的移动，绕X轴的转动和绕Y轴的转动。

2　静力分析

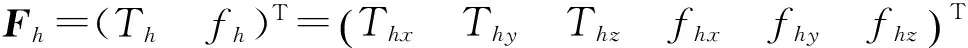
(2)

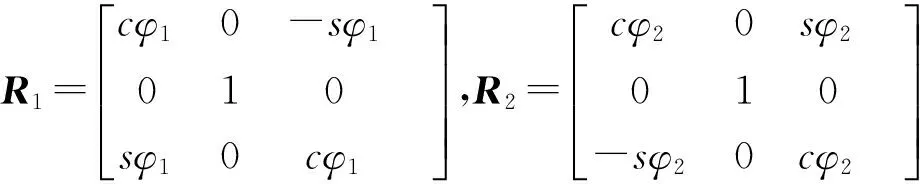
(3)

其中φi为各转动副转角。分支i上下杆件分别用u和s表示，那么各运动副上的6维合外力沿{ki}分解可得：

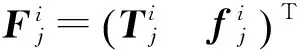
(4)

此外，分支i中上下杆件向质心简化的6维合外力，在{ki}下表示为：

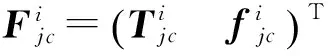
(5)

将分支运动副约束反力沿{ki}3个轴方向分解。各运动副受力特点为：R副沿轴线方向无约束力矩，S副无约束力矩，移动副沿轴线方向无约束力。

分别选取整个分支AiBi、分支AiBi的下部杆件和动平台为研究对象，建立力平衡方程和力矩平衡方程。整个分支AiBi、下部杆件和动平台的受力如图2—图4所示。

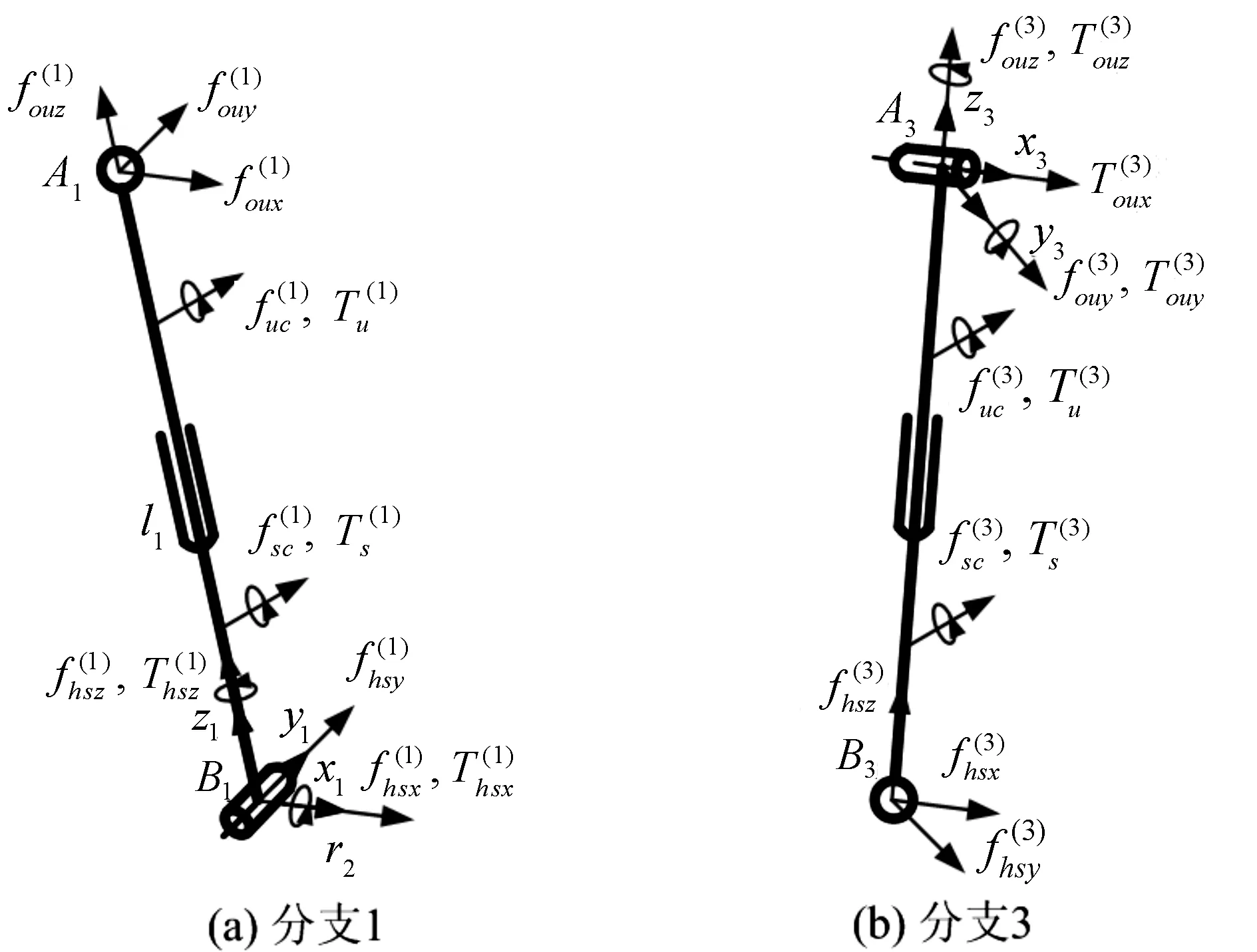
图2　分支整体受力

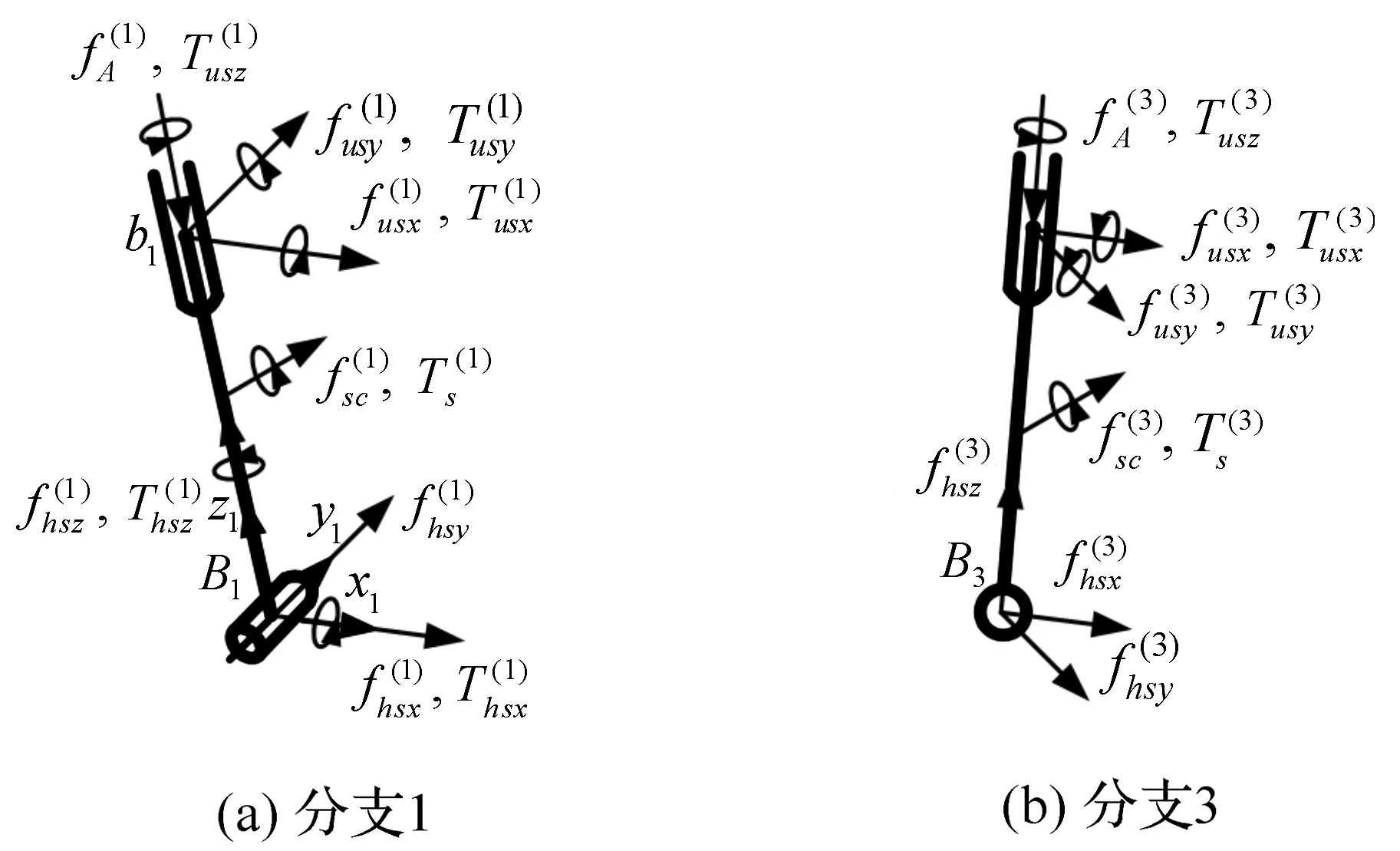
图3　分支下部受力

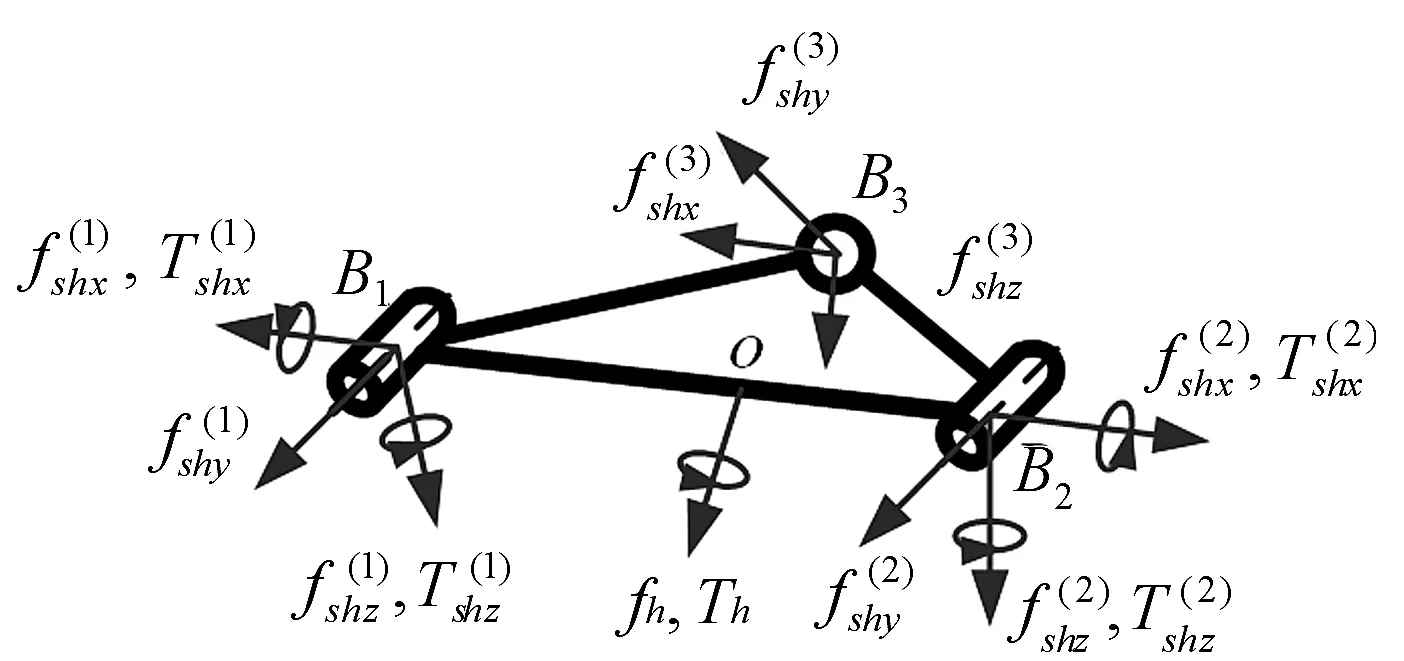
图4　动平台受力

整个分支AiBi的力平衡方程为：

(6)

分支1、2对Bi取矩，得力矩平衡方程为：

(7)

分支3对A3取矩，得力矩平衡方程为：

(8)

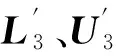
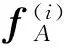
(9)

分支1、2下部杆件对Bi取矩，得力矩平衡方程为：

(10)

分支3下部杆件对B3取矩，得力矩平衡方程为：

(11)

动平台的平衡方程为：

(12)

从而，对1、2杆对Bi点取矩得：

(13)

(14)

而第3杆对A3点取矩有：

(15)

各分支上部分力平衡有：

(16)

动平台力与力矩平衡有：

(17)

写成系数矩阵形式为：

(18)

其中：

(19)

3　数值计算

表1所示为机构实际尺寸和载荷参数。

表1　参数设置

将瞬时惯性力与力矩设置为0，即：

(20)

由于2-SPR-RPS并联机构动平台运动相互耦合，故可将3个自由度运动拆解进行分析，即进行自由度解耦，如图5所示。其中图5(a)所示为第1种情况，即动平台沿z轴方向移动；图5(b)所示为第2种情况，即动平台绕y轴转动；图5(c)所示为第3种情况，即动平台绕X轴转动。

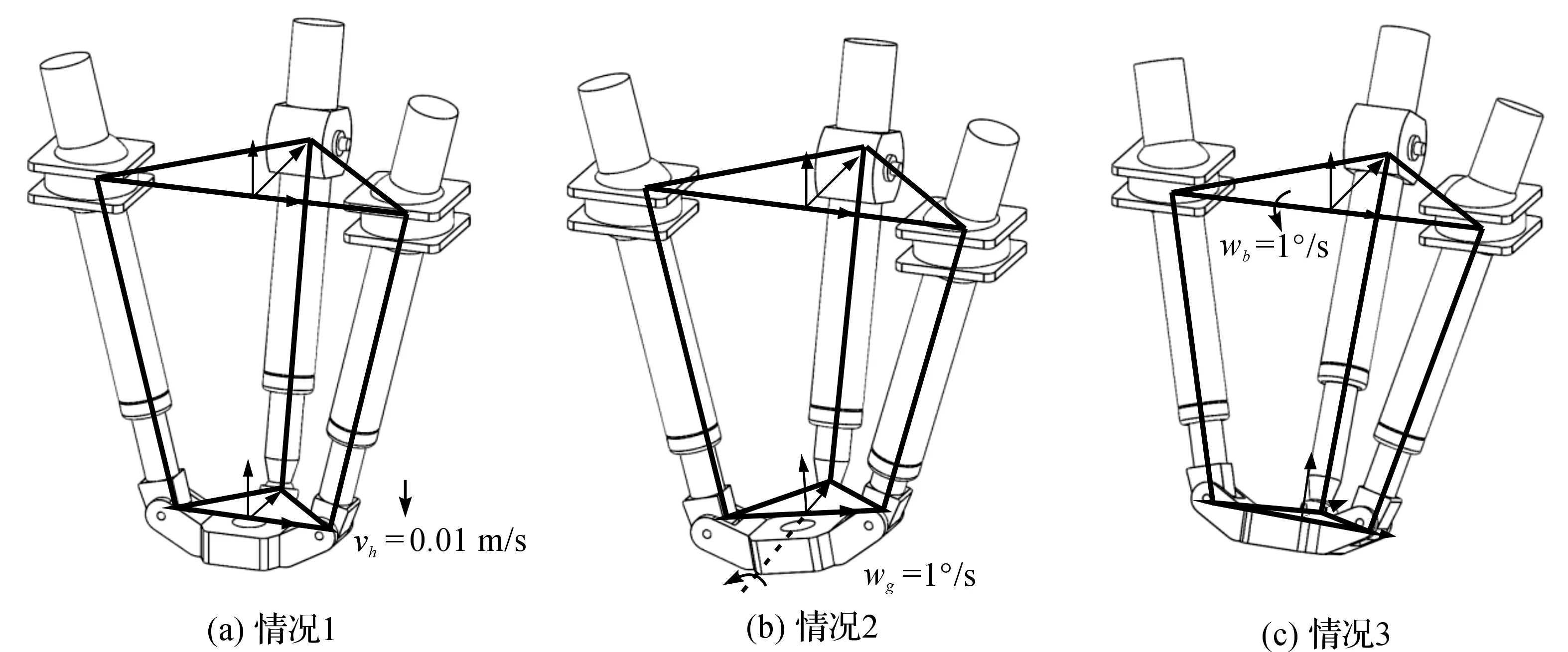
图5　机构分解运动

3.1情况1，仅改变h

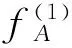
3.2情况2，仅改变γ

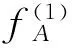
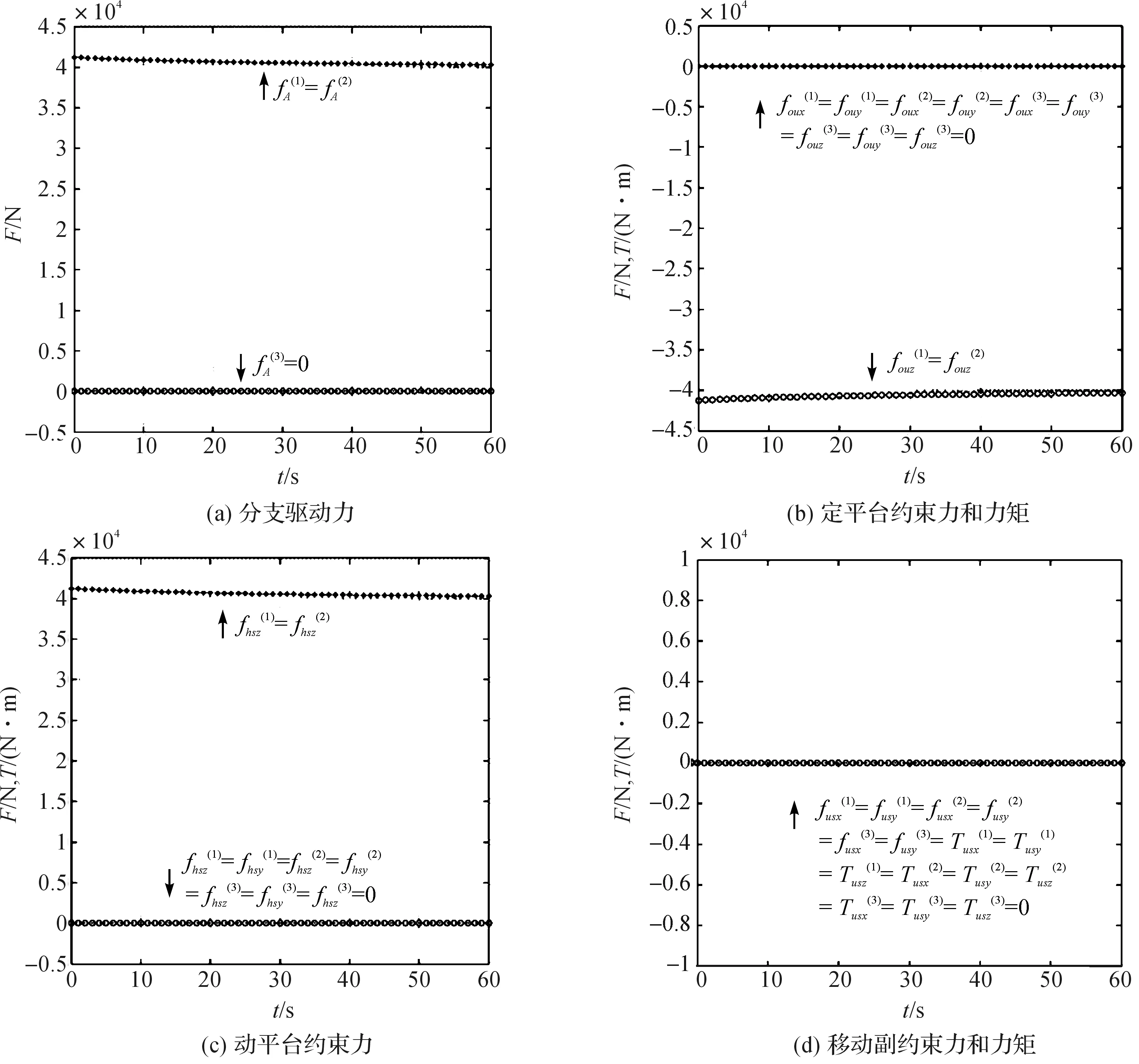
图6　情况1下驱动力及约束力曲线

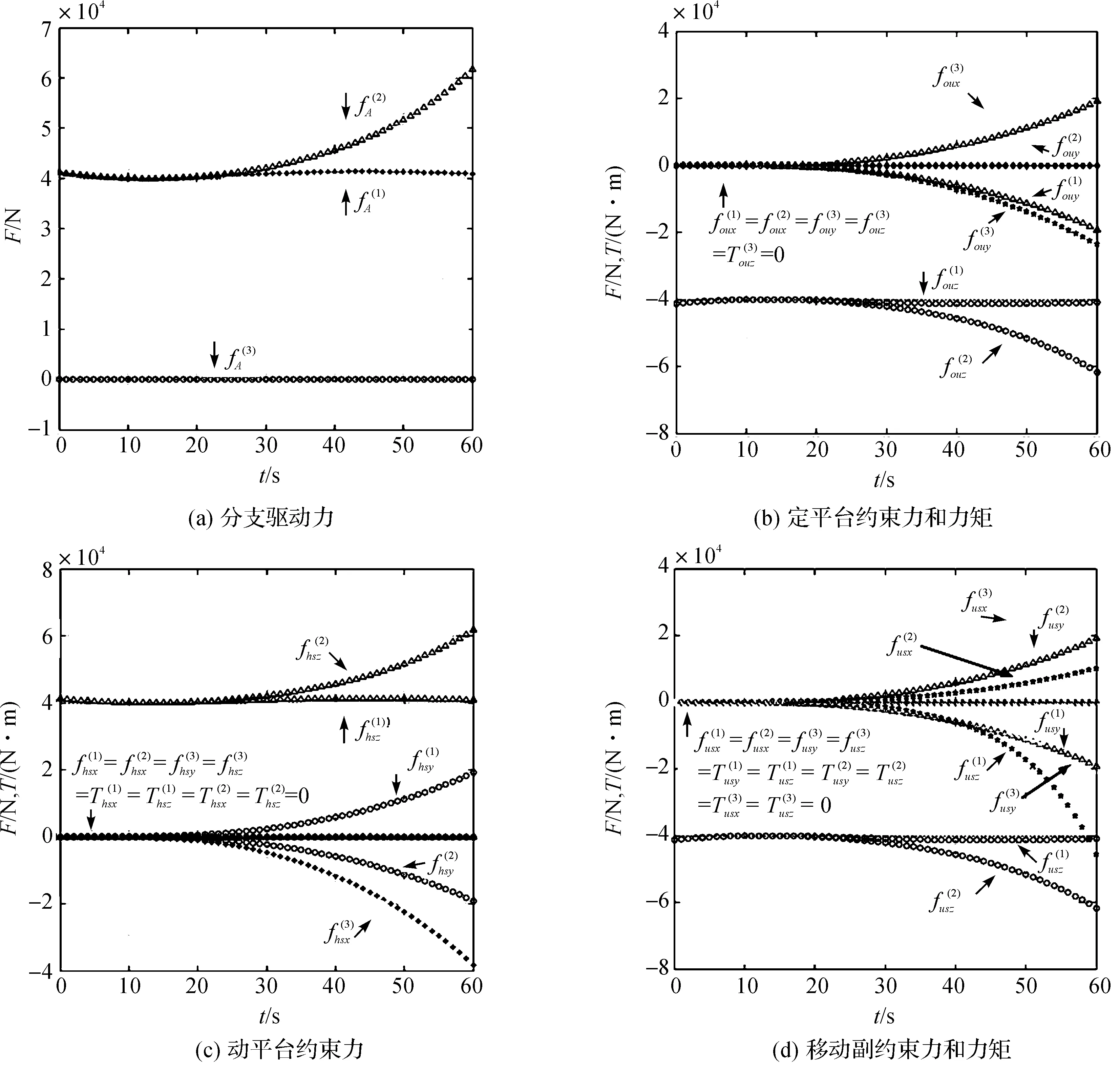
图7　情况2下驱动力及约束力曲线

3.3情况3，仅改变β

保持z和γ不变，β发生变化，角速度为ωβ=1°/s。该情况下驱动力及约束力曲线如图8所示，1、2分支驱动力相同且第3分支不提供驱动力。随着β的增大，第1、2杆的驱动力逐渐减小。这种情况下驱动力与各运动副上约束力曲线与第一种情况相似。以驱动力为例，两者趋势基本相同，不同之处在于前者为凹函数，后者为凸函数。

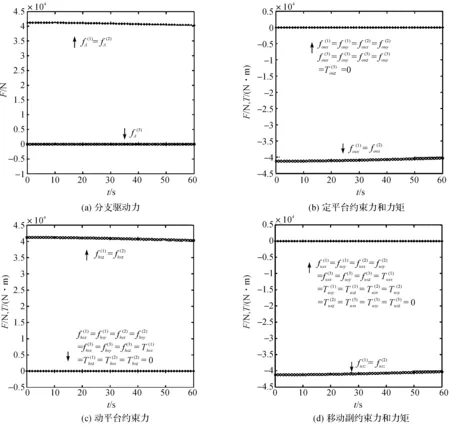
图8　情况3下驱动力及约束力曲线

对比这3种情况作可以发现，情况2下驱动力和运动副约束力的变化幅度均比较剧烈，且最大幅值最高。因而在机构设计时，需充分考虑沿x轴转角的影响以及在这种严苛条件下的强度。

通过这种3自由度拆分单变量的计算，可简便地计算力/力矩的变化，进而可以研究多变量下的变化情况，例如：保持h不变，γ和β同时发生变化，变化范围均为0°～60°，驱动力及约束力变化关系如图9所示。

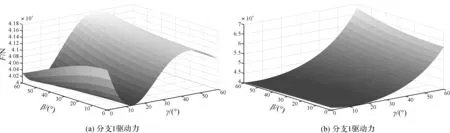
图9　多变量下驱动力变化情况

4　结　论

本文对一种应用于搅拌摩擦焊的2-SPR-RPS并联机构进行静力分析。由于该机构末端执行器受耦合力作用，需对其进行静力解耦。解耦方法基于自由度分析，该分析表明机构具有1个移动和2个转动自由度。通过拆杆，可建立各杆件6维力承载方程。将动平台运动按机构自由度分解，可获得该机构各支链和动平台运动关节随运动参数变化的驱动和约束力曲线。其中，绕x轴的转角γ对该并联机构驱动力及其他运动副约束力的影响最大。静力分析能够为2-SPR-RPS并联机构的电机参数选取、强度设计、刚度设计等提供基础数据。

[1] 黄真,赵永生,赵铁石.高等空间机构学[M].北京：高等教育出版社,2006:127-138.

[2] 黄真,李秦川.少自由度并联机器人机构的型综合原理[J].中国科学：技术科学,2004,33(9):813-819.

[3] 路懿,胡波.少自由度度并联机构研究进展[J].燕山大学学报,2011,35(5):377-384.

[4] 艾青林,黄伟峰,张洪涛,等.并联机器人刚度与静力学研究现状与进展[J].力学进展,2012,42(5):583-592.

[5]MERLETJP.Jacobian,manipulability,conditionnumber,andaccuracyofparallelrobots[J].Journalof

MechanicalDesign,2006,128(1):199-206.

[6]TSAILW.RobotAnalysisandDesign:theMechanicsofSerialandParallelManipulators[M].NewYork:JohnWiley&Sons,1999:261-286.

[8]GOSSELINCM.Stiffnessmappingforparallelmanipulators[J].IEEETransactionsonRoboticsandAutomation,1990,6(3):377-382.

[9]RUSSOA,SINATRAR,XiF.Staticbalancingofparallelrobots[J].MechanismandMachineTheory,2005,40(2):191-202.

[10] 赵燕,黄真.3-RPS并联机构的主动力和约束力分析[J].燕山大学学报,2008,32(4):299-303.

[11] 赵燕,黄真.含过约束力偶的少自由度并联机构的受力分析[J].机械工程学报,2010,46(5):15-21.

[12] 李永刚，宋轶民，黄田，等.少自由度并联机器人机构的静力分析[J].机械工程学报,2007,43(9):80-83.

[13] 高峰,陈玉龙,彭斌杉,等.新型解耦和各向同性五维力传感器性能分析[J].机械工程学报,2004,21(6):54-57.

[14]LUY.UsingvirtualworktheoryandCADfunctionalitiesforsolvingactiveandpassiveforceofspatialparallelmanipulators[J].MechanismandMachineTheory,2007,42(7):839-858.

(责任编辑： 康锋)

Static Analysis of 2-SPR-RPS Parallel Manipulator

ZHANGNingbina，XIANGJinana，LIQinchuana，CHENQiaohongb

(a.Faculty of Mechanical Engineering & Automation,；b. School of Information Science and Technology, Zhejiang Sci-Tech University, Hangzhou 310018, China)

2-SPR-RPS parallel manipulator has one translational degree of freedom (DOF) and two rotational DOFs, which can be used for friction stir welding robot. In real working conditions, the external wrench exerted on the end-effector is complex, and is born by the mutiple coupling branches. Therefore, static analysis of the manipulator is necessary. First of all, the vector method was used to establish wrench equations. After that, the DOFs of the parallel manipulator were decoupled by adjusting two rotation angles and the stroke, respectively. Then, the mapping between the configuration of the manipulator and the constraint or actuation wrenches of joints was obtained. Finally, univariate parameters were combined again to get complete static wrench diagrams. The research results offer guidance for driver selection, joint bearing analysis and structural strength design of the 2-SPR-RPS parallel manipulator.

parallel manipulator; lower-mobility; static analysis; vector method

10.3969/j.issn.1673-3851.2016.09.014

2015-10-22

国家自然科学基金项目(51275479)；浙江省自然科学基金项目(LZ14E050005)；机械工程浙江省重中之重学科和浙江理工大学重点实验室开放基金项目(ZSTUME01A07)

张宁斌(1990-)，男，浙江宁波人，硕士研究生，主要从事并联机器人方面的研究。

陈巧红，E-mail：chen_lisa@zstu.edu.cn

TP24

A

1673- 3851 (2016) 05- 0713- 07 引用页码： 090401