精准把脉教材 激活教材主题图

江苏常州武进清英外国语学校（213164）　沈　静



精准把脉教材激活教材主题图

江苏常州武进清英外国语学校（213164）沈静

在现行的数学苏教版教材中，主题图是一个大的亮点。但教师在实际使用“主题图”时会存在着许多误区：弃置不用、随意更换、本末倒置或机械使用，在一定程度上会影响教学目标的有效达成。因此教师在实际教学中应在充分把握教材的基础上，对主题图进行有效地处理，从而使“主题图”成为学生提高学习能力的有效载体。

教材主题图灵活运用

在努力实现活力课堂这个愿望的过程中，有一个重要环节需要教师重视：如何依据课程标准基本理念，在充分理解、尊重教材的基础上，用好、用活教材，从而达到高位引领课堂的目的？

一、精准把脉教材，课堂教学的前奏

对于研读教材，应该从三个不同层次去努力：一是熟悉教材全部内容；二是掌握教材各种题型编排的意图，牢记教材的章节、单元知识；三是精准把脉教材。做到这三个层次，才可以说对教材精准把脉。

【例题图：一年级·两位数加两位数（进位加）】

在学生自己收集信息，提出问题的基础上，教师列出算式“34+16”。

师：谁知道结果呀？

师：告诉老师你怎么算的？

师：说说口算过程和笔算方法。

教师在学生叙述的基础上补充讲解算理，然后再让学生模仿板书，计算一遍，从而达到熟练掌握的目的。事实上，教材编写的步骤是先借助摆小棒、拨算珠等实践活动来感知算理，再慢慢归纳其中算法，形成算式。

下面是例题主题图下的操作演示过程：

操作演示过程体现了教材编排两个层面的思维水平：一是基于形象的思维；二是基于符号或逻辑的思维。教材编写意图是让学生的思维由形象上升到符号或逻辑。然而在上述教学案例中，由于教师对教材的编排意图不明确以至于课堂效率低下，无法完成教学内容。

虽然低年级学生抽象思维水平比较低，但学生是有类似题目的感知经验；部分学生可以直接进行口算（或笔算），而无需借助实物（或学具）。为此教师追问：

（1）部分学生的准确率能否代表全班学生的水平？

（2）学生直接口算（笔算），是否真正理解了呢？

（3）会不会是学生长期进行算式训练形成惯性，而缺乏借助实物进行思考呢？

（4）是不是学生处于思维便捷的需要，直接跳到了口算或笔算的思维层次，但实际上还缺乏感性的基础？

了解学生真实的思维状态，为教师教学采取正确的策略或方法提供了依据。而事实矛盾是学生对进位原理理解不清，这就需要通过适当的操作认识进行补充，丰富其感性经验。

二、有效研发教材，课堂教学挖深度

在课程实施中，教师应该以教材为载体，结合其他资源来组织学习活动，不能陷入仅做教材内容的传声筒与发言人的误区。为此，教师需要对教材进行再次研究，使师生学习活动能够纵向发展，让课堂教学充满智慧。

【习题图：苏教版六年级数学·圆柱与圆锥】

教材的编排意图：让学生辨别圆柱、圆锥的直径倍数关系不等于底面积倍数关系。

（四个圆柱序号依次是①、②、③、④）

师：我们先猜测一下，圆锥与哪个圆柱的体积相等？

生1：圆锥和第②个圆柱体积相等。

生2：圆锥和第③个圆柱体积相等。

师：同学们，能说说你们的理由吗？（小组探究）

交流1：第①个圆柱与圆锥等底等高，所以圆柱体积是圆锥的3倍；第②个圆柱和圆锥高是相等的，但底面积不相等，也不是3倍关系，所以体积不相等；第④个从视觉上就觉得圆柱的体积不可能与圆锥相等。

交流2：圆锥：3.14×4.5×4.5×12÷3；

圆柱①：3.14×4.5×4.5×12；圆柱②：3.14×1.5×1.5×12；

圆柱③：3.14×4.5×4.5×4；圆柱④：3.14×1.5×1.5×4。

通过上述算式可推断圆锥与圆柱③的体积相等。

交流3：我发现圆柱①的体积是圆锥的3倍，也是圆柱③的3倍，所以圆柱③的体积等于圆锥的体积。

【二次探究】

教师追问：“同学们通过各种方法来验证它们之间的体积关系，很不容易。刚才有同学发现，圆锥与圆柱底面积之间有一定的关系，再仔细观察，看看还能发现什么？”

（小组之间再一次展开了讨论与研究）

交流4：

（1）圆柱①和圆锥等底等高，所以圆柱①的体积是圆锥的3倍；

（2）圆锥的底面积是圆柱②的9倍，高相等，那么圆锥的体积是圆柱②的3倍；

（3）圆锥的底面积和圆柱③相等，高是圆柱的3倍，所以它们的体积相等；

（4）圆锥的底面积是圆柱④的9倍，高是它的3倍，所以圆锥的体积是圆柱④的9倍。

师：观察圆锥和圆柱③，你有什么大胆的设想吗？

生：我认为体积相等、底面积相等的圆锥和圆柱，圆锥的高是圆柱的3倍。

师：同学们，再大胆猜想一下，假如圆锥和圆柱的高相等，体积相等，它们的底面积会有什么关系呢？

生：圆锥的底面积是圆柱的3倍。

纵观上面的教学过程，尊重教材，精准把脉，有效研发教材习题，拓展猜想与验证的空间，让学生体验知识形成的过程，了解知识之间的脉络体系，在课堂上挖深度。

三、超越教材资源，课堂教学上高度

教师观要求教师成为教材的研发者，而不是做传统的教书匠，要突破教材对学生教育的束缚，有创造性地使用教材。在教学过程中，既尊重教材，又不囿于教材。

【习题主题图：苏教版四年级·角】

通过测量，学生纷纷发言。

生1：我发现同一个图形中的每个角都相等。

生2：四边形的内角和是360°。因为四边形可分成两个三角形，而三角形内角和是180°。

师：真棒！四边形转化成三角形，通过三角形的内角和求四边形内角和。鼓掌！同学们，用类似的方法你能求出五边形、六边形的内角和吗？

生3：五边形分成了3个三角形，五边形的内角和是180°×3=540°，六边形分成了4个三角形，六边形的内角和是180°×4=720°。

生4：我发现图形每增加一条边，内角和就增加180°。

师：如果不画图，也不测量，你能知道七边形、八边形的内角和吗？挑战一下。

生5：七边形内角和是720°+180°=900°，八边形内角和是900°+180°=1080°，老师，我发现这是有规律的。

生6：三角形的内角和是180°，

四边形的内角和是180°×2=360°，

五边形的内角和是180°×3=540°，

六边形的内角和是180°×4=720°，

七边形的内角和是180°×5=900°

……

由此可以得出，多边形的内角和就是180°×（边数-2）。

在测量后，通过观察、思考、比较，学生已经有了丰富的发现，这道习题的教学目标就圆满完成。这样基于教材中的三角形、四边形、五边形、六边形，延伸到七边形、八边形，再到任意多边形，拓展了“空白资源”，也使课堂教学层次上了高度。

四、大胆创新教材，课堂效益最优化

教材无非是个载体。在理解“教材顺从教学，还是教学顺从教材”上，教师应该始终坚持“教材服务于教学，依从学生”这个观点。教材的创新是教师的一项权利，但也不可滥用。只有从编写者角度去审视教材，掌握学生的学情，切实找到教材与学生结合点，这样才能对教材进行大胆的取舍和有效的改造。

【例题图：《正比例和反比例》】

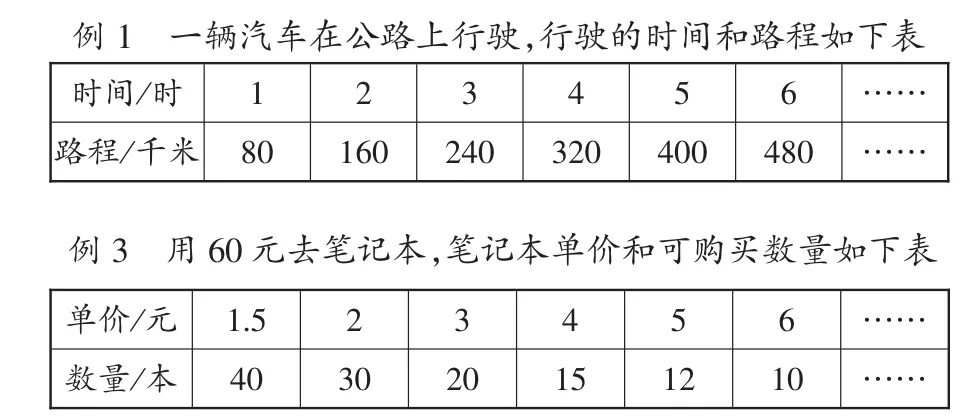
教材通过以上2个图表分别阐述正、反比例的意义，各占用1个课时。经过新教材与老教材的对比，发现新教材对正、反比例的定义形式发生了重大的改变，新教材采用用描述性定义，目的是为了降低抽象性。经过反复研读，我大胆整合教材，把正反比例合并在一课进行教学。以下是简单的整合过程。

首先导入，理解关联的量，根据变化方向进行首次分类。在此基础上进行同向比较，定义正比例；反向比较，定义反比例。再进行对比练习，在学生已经认识正反比例的基础上将举例法优化为推理法，从具体量过渡为一般量，从而从整体上把握正反比例意义。最后再进行有效的综合练习。

教材弱化了学生对数量关系的理解，而是通过具体的情境让学生慢慢体会。基于教材的编排意图，可以从一个全新的数学角度来研究，用一种崭新的数学思想来理解。因此，大胆重组教材，有效落实教学的三维目标。

《义务教育数学课程标准》指出，学生的数学学习应当是一个生动、活泼、主动的过程。改变教与学的方式，创设“学生感兴趣的数学情境”，引导学生观察分类、自主探索、合作交流，呈现学生“分类方法”的多样化，在两次“分类”中不断激发学生探究两种关联量变化规律的热情；在不断探究两种关联量变化规律的活动中体验探索成功的乐趣；在不断的认知冲突中达到思维的辩证统一，从而使课堂效率达到最高。把脉教材，从用“好”到用“活”。最大限度地使用一切教学资源，有效地进行课堂教学，高屋建瓴，使数学课堂充满生命活力。

（责编罗阳）

G623.5

A

1007-9068（2016）20-044