2015年高考北京理科数学第19题的探究与反思

◇　广东　陈国毫

(作者单位：广东省佛山市南海区西樵高级中学)



2015年高考北京理科数学第19题的探究与反思

◇广东陈国毫

以问题为载体、知识为基础、思维为主线、能力为目标,全面考查学生的学习潜能和数学素养,是当前高考命题的一个重要方向.在每年全国各地的高考中,圆锥曲线必有1道大题,其中往往综合考查等价转化、数形结合、分类讨论、函数与方程等数学思想,以及定义法、配方法、待定系数法、参数法等数学通法.试题体现能力立意、强调思维空间,对学生的数学素养要求较高.很多学生往往做了第(1)问,后面的问题或因文字多、符号繁、探索味道浓、运算量大、思路不清晰而望尘莫及.因此对圆锥曲线的研究,特别是在高三复习课上对圆锥曲线综合题的解决,应当选择合适有效的处理方式.以下笔者结合2015年高考北京理科数学第19题,谈谈自己的一些想法.

1　原题展示

(1) 求椭圆C的方程,并求点M的坐标(用m、n表示);

(2) 设O为原点,点B与A关于x轴对称,直线PB交x轴于点N.问:y轴上是否存在点Q,使得∠OQM=∠ONQ?若存在,求点Q的坐标;若不存在,说明理由.

2　解法剖析

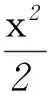
第(2)问实则考查对几何性质的探究.图形中点对称、直线与x轴的交点、所研究的角的位置,这些直观的几何特征是处理问题的关键.采用坐标法,显化M、N、Q的坐标形式,分别为

利用tan∠OQM=tan∠ONQ,确定坐标中涉及的变量之间的关系

3　背景探源

本题改编自人教版《选修4-4》第34页习题2.2第2题.

从核心方法上分析,都注重运用代数的方法量化几何关系.

从形式上看,二者高度相同:都以焦点在x轴的椭圆(尽管例2没有指明a>b>0这个条件,但是通过分析这个条件是隐含的)为载体,点关于x轴对称(例2短轴的端点显然对称),过对称点的直线与x轴有交点;涉及的求解对象都与x轴有关.区别在于例1研究的是角度的恒等问题,例2研究的是线段长度的定值问题.

类似的以此题为背景的,还有如下题目:

图1

(1) 求椭圆的标准方程.

(2) 探究:|OP|·|OQ|是否为常数.

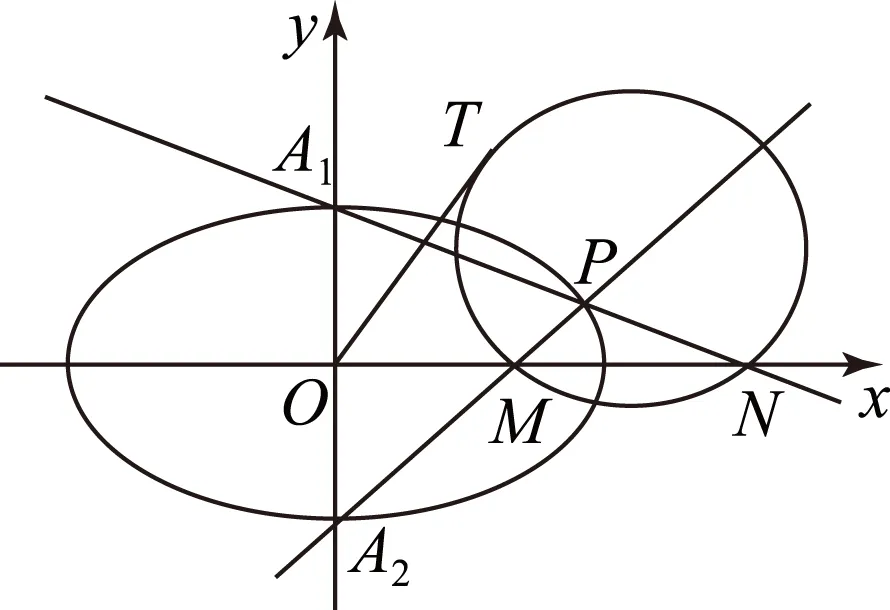
图2

(1) 求椭圆E的方程.

(2) 设椭圆E的上、下顶点分别为A1、A2,P是椭圆上异于A1、A2的任一点,直线PA1、PA2分别交x轴于点N、M,若直线OT与过点M、N的圆G相切,切点为T. 求证：线段OT的长为定值,并求该定值.

图3

(1) 求椭圆C的方程.

(3) 设点P是椭圆C异于M、N的任一点,且直线MP、NP分别交x轴于点R、S,O为坐标原点,求证:|OR|·|OS|为定值.

例4中2个顶点A、A1关于x轴对称,由切割线定理得OT2=OM·ON,问题转化为线段长度的定值问题;而例5中,由椭圆与圆的对称性可知,点M、N关于x轴对称,问题也是求线段长度的定值问题.

4　一般结论

对以上3个类似题进行对比,不难发现,2个对称点是椭圆上任意给定的,点P亦然,并异于2个对称点.而结论涉及的线段长度的乘积恒为定值.而例1第(2)问,其实是源于这个一般性结论的推论.

|OP|·|OQ|=a2.

同理可得直线A1B:

陈友益(2018)研究了影响供应链金融发展的因素。在整个链中上下游、多级企业存在一些操作、法律、市场等的风险。会影响其发展。

则|OP|·|OQ|=|xP·xQ|=a2.

|OP|·|OQ|=b2.

|OP|·|OQ|=b2.

|OP|·|OQ|=a2.

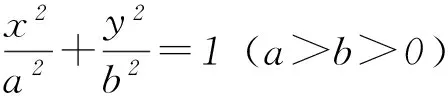
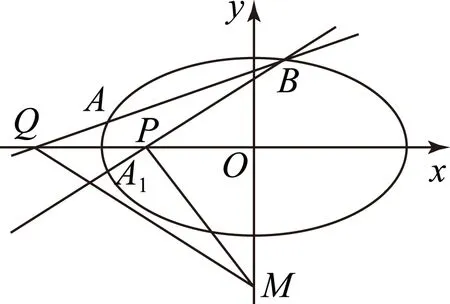
图4

证明结合图4可知,

5　拓展

类比椭圆,可以将上述的结论推广至双曲线.限于篇幅,这里不一一列举,有兴趣的读者可以类比上述的方法进行求证,或者用几何画板进行验证.

下面探讨抛物线在满足上述条件的情况下,会有什么性质.

性质2设抛物线y2=2px(p>0)上2个点A与A1关于x轴对称,B是抛物线上异于A与A1的任一点,直线AB、A1B与x轴分别交于点M、N,则有|OM|=|ON|.

推论3设抛物线y2=2px(p>0)上2个点A与A1关于x轴对称,其准线l与x轴的交点为N,连接NA交抛物线于点B,则A1B必过焦点F.

推论4设抛物线y2=2px(p>0)的准线l与x轴的交点为N,F为抛物线的焦点,A是抛物线上任一点,直线NA交抛物线于点B,直线BF交抛物线于点A1，则直线NA与NA1关于x轴对称.

6　反思

1) 通性通法齐把握.

所谓通性通法是指解决具有相同性质数学问题所用的通用方法,通性通法是数学思想和数学方法在解决问题中的集中体现.就现阶段而言,中学生应该掌握的最基本的通性通法应是具有某些规律性和普遍意义的常规解题模式和常用的思想方法.解析几何的基本思想是用代数的眼光来看待平面几何问题.用代数的方法研究圆锥曲线的性质,实质上是将对复杂的几何关系的考查转化为对曲线方程特点的考查,因为代数方法可以程序化地进行运算、操作,可以使研究过程更有规律可循.

2) 对比变式相结合.

所谓变式是指教师有目的、有计划地对命题进行合理的转化,如：不断地变更命题中的非本质特征;变换问题中的条件或结论;转换问题的内容和形式;配置实际应用的各种环境,使数学内容的非本质特征时隐时现，而本质特征保持不变.就高三复习阶段而言,教师在评讲、处理练习时,应给学生渗透的思想不应止步于最终答案的获得.问题得到了答案,并非意味着解题过程的完成,对待解决问题态度,除了透彻理解自己的思路、解法外,还应该考虑能否用不同的方式去解决问题.当问题的解答冗长而复杂时,自然会揣测是否存在着某种更清楚且少迂回的解法,即使成功地找出一个令人满意的解法,也不必有大功告成的感觉,而应该考虑是否还有其他做法,然后对不同解法加以比较,看看哪个最本质，哪个最简单，哪个最完美.同时,教师应以试题研究为阵地,充分利用题目之间的相似性进行比较,就其共同点概括问题的本质,将问题进行变式推广,教学生如何去分类处理、研究反思,完善学生的认知结构,增强数学知识结构的系统性.只要弄清问题本质上的共性,就会应用解答的同一模式去处理类似的问题.

总之,数学教学的本质是学生在教师的引导下能动地构建数学认知结构,使自己得到全面发展的过程.而其中最重要的是让学生把握问题处理的通性通法,明白数学知识的迁移是丰富多彩的，题目之间的联系是非常紧密的.数学的学习不是埋于题海、盲目追求数量,而是真正了解数学问题变化的规律,掌握这种变化背后的本质联系,学会解决变式,学会设计变式、拓展问题，提高自身的数学能力和数学素养.

(作者单位：广东省佛山市南海区西樵高级中学)