一道学科能力展示试题的背景探源

◇　北京　　　　张留杰　童嘉森(特级教师)

(作者单位:1.北京市陈经纶中学　2.北京市第八十中学



一道学科能力展示试题的背景探源

◇北京张留杰1童嘉森2(特级教师)

2015年12月13日的“第八届全国中学生数理化学科能力展示活动”已落下帷幕,笔者感觉高二数学试卷的第15题内涵丰富、值得深思,下面是对该试题的证明和探究.

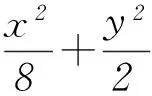
1　题目的解答

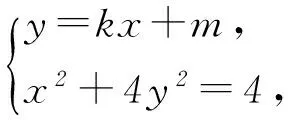
Δ=64k2m2-16(1+4k2)(m2-1)>0,

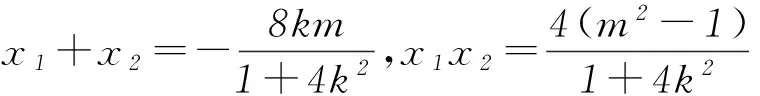
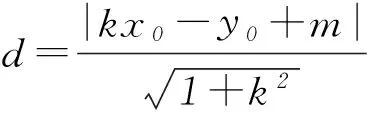
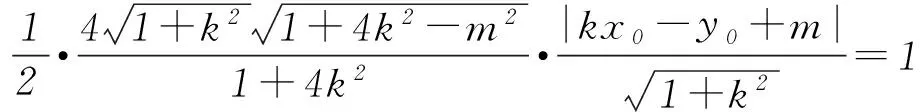
①

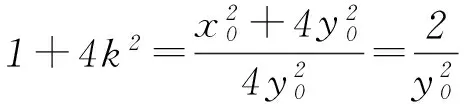
②

易得t=1是该方程的一个解.

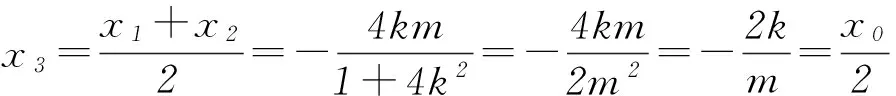
所以点Q(x3,y3)也是线段OP的中点,OP与MN互相平分,所以四边形OMPN为平行四边形(特别的,当M、N2点分别在坐标轴上时,四边形OMPN为矩形).所以

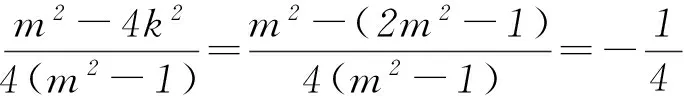
图1

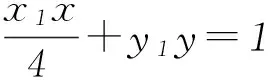
2　试题的背景探源

波利亚在《怎样解题》中指出:回顾已经完成的解答是工作中的一个重要且有启发性的阶段……去回顾他所做的一切,可能有利于探究他刚才克服的困难的实质.回顾此题,不难发现这是一道与“相似椭圆”有关的问题,它充分体现了2个特殊的相似椭圆的性质,下面给出试题背后所蕴含的一般性结论,也是命制该试题的根源所在.

图2

1) 四边形OMPN为平行四边形;

3) 四边形OMPN的面积为定值ab;

4)A、O、B3点共线.

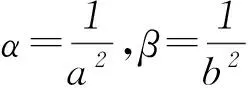
PM:αx1x+βy1y=1,PN:αx2x+βy2y=1.

将点P(x0,y0)的坐标代入得αx1x0+βy1y0=1和αx2x0+βy2y0=1,所以切点弦MN所在直线方程为αx0x+βy0y=1.

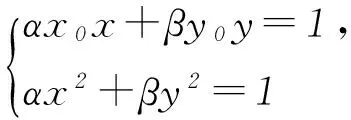
2) 由1)知PA∥ON、PB∥OM,所以

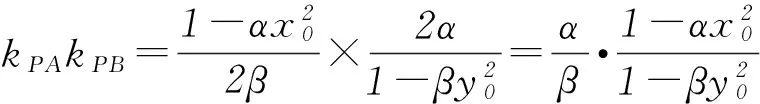
SOMPN=|x1y2-x2y1|=

同理可得点N是切线PB的中点,又PO的中点Q在中位线MN上,所以

∠POA+∠POB=∠PQM+∠PQN=180°,

所以A、O、B3点共线.证毕.

因此根据原题目的条件和结论,不难发现将结论1中的条件和结论重新组合,且a=2,b=1,即可编制出此能力展示试题.

我们还猜想该竞赛题具有一般结论:

图3

1) 四边形OMPN为平行四边形;

2)PM、PN与椭圆C1相切.

(请感兴趣的读者自行证明).

(作者单位:1.北京市陈经纶中学2.北京市第八十中学