钢弹簧浮置板轨道结构模态分析

江阿兰，李建敏

(大连交通大学 土木与安全工程学院，辽宁 大连 116028)*



钢弹簧浮置板轨道结构模态分析

江阿兰，李建敏

(大连交通大学 土木与安全工程学院，辽宁 大连 116028)*

利用ANSYS软件，对浮置板结构进行三维的模态分析.得到不同参数下轨道的固有频率，分析每个参数对钢弹簧浮置板轨道结构固有频率的影响规律，为以后的研究者提供参考.经过分析对比，在众多的参数中，钢弹簧刚度和间距是影响固有频率的两个重要参数，应重点进行研究.

浮置板轨道结构；模态分析；固有频率

0　引言

地铁作为一种可以很好的缓解交通堵塞问题的交通工具并且以其节省土地、减少噪音、节约能源、减少污染等诸多优点而受到人们的青睐.然而地铁工程在给人们带来方便的同时，也带来了噪声的问题，所以从世界上第一条地铁运营之日起，人们对于地铁减振降噪方面的研究也就从未停止过.钢弹簧浮置板轨道作为目前减振降噪效果最好的一种轨道结构形式，在国外已经具有几十年的使用历史.在我国北京地铁西直门站首次引进该轨道结构，通过运营实践收到非常好的减振降噪效果，而后在天津地铁、沈阳地铁、杭州地铁等各大城市地铁中得到广泛运用.

降低浮置板轨道结构的固有频率是地铁减振降噪的关键所在，而浮置板轨道结构是一个系统工程，组成部分较多，因此影响该结构固有频率的因素也很多.本文通过有限元软件建立钢弹簧浮置板轨道结构的三维有限元模型，通过改变扣件刚度、钢弹簧刚度、钢弹簧间距、浮置板长度、浮置板密度、曲线段半径等参数，得到该结构固有频率，并分析每种参数对固有频率的影响规律.

1　钢弹簧浮置板轨道结构模型建立

利用有限元软件模拟浮置板轨道模型，不但要如实地反应浮置板轨道结构的实际情况的力学特性，而且尽可能的应用较少的单元与简单的单元形式[1]，从而在能减少计算工作量的同时又能保证较高的计算精度.本文模型的建立参考了杭州地铁一号线某段钢弹簧浮置板轨道道床，该段位于盾构区间内，全部位于圆曲线上，曲线半径为300 m，超高为60 mm，超高方式采用半超高的方式.如图1.

图1　钢弹簧浮置板轨道结构示意图

1.1计算单元参数的选择

固体单元用于模拟三维的固体结构，用于模拟浮置板轨道床的单元应具有塑性、蠕变、膨胀、应力强化、大变形和大应变的能力，本文选择SOLID45单元用于模拟浮置板轨道道床，浮置板的弹性模量为20、32.5、45和57.5 GPa，泊松比为0.2，密度选择2 200、2 500、2 800、3 000、3 300 kg/m3五种选择，浮置板长度选择3、6、9、18、30 m五种，板与板之间通过剪力铰联接，在模拟时通过节点自由度耦合联接相邻的两块板.

由于钢弹簧浮置板轨道结构中的钢筋非常的密集，而钢筋在浮置板中主要承受拉应力的作用，因而钢筋可以采用适合的泊松比和弹性模特来代替，在本文中钢筋选择和浮置板相同的泊松比和弹性模量，两者完全耦合在一起.

钢轨作为轨道的重要部分，直接承受并传递列车的压力、冲击以及振动，同时钢轨可以看做一个等截面的无限长的结构物，在进行有限元分析时，将钢轨看做无限长的离散点的梁.在建模时采用BEAM188模拟钢轨并进行有限元分析.钢轨的有限元参数为弹性模量210 GPa，泊松比为0.3.

钢轨的扣件采用一个横向弹簧和一个纵向弹簧进行模拟，选用COMBIN14进行模拟，同时考虑扣件阻尼的效应.选用的参数刚度有10、15、20、25、30 kN/mm五种选择；扣件阻尼均为5 N·s/m.

钢弹簧同样采用一个横向弹簧和一个纵向弹簧进行模拟，选用的单元也为COMBIN14.选用的参数刚度分别为4、6、8、10、12 kN/mm；阻尼均为7 N·s/m；钢弹簧的间距有0.5、1.0和1.5 m三种.1.2建立有限元模型

利用有限元软件ANSYS，选择合适的参数建立有限元模型，如图2.

图2　钢弹簧浮置板轨道三维模型图

1.3模态分析

对于建立的有限元模型进行模态分析，选取前九阶频率.如表1.

表1　钢弹簧浮置板轨道前九阶固有频率

2　各种参数的影响

2.1扣件刚度的影响

扣件作为连接钢轨和轨枕的一个重要构件，应作为一个重要参数进行研究，下面选择不同的扣件刚度研究轨道固有频率的变化，以研究扣件对浮置板结构的力学性能是否有影响.扣件刚度变化对浮置板轨道固有频率的变化规律如图3(以扣件刚度10 kN/mm为基准刚度)所示.

图3　扣件刚度对固有频率影响变化图

随着扣件刚度的增大，钢弹簧浮置板轨道的固有频率有所增大，但从图上可以看到变化范围很小，第一阶固有频率从4.302 1 Hz增加到4.302 2 Hz，增加仅仅0.000 1 Hz；第二阶频率由11.615Hz增加到11.618 Hz，也仅仅增加了0.003Hz；即便是第十阶固有频率从61.528 Hz增加到65.958 Hz，增加了4.43 Hz，相比基准固有频率增加幅度也很小，增加了7.2%.综上扣件刚度的变化对系统固有频率影响不大，故在探究浮置板轨道减振降噪效果时，可以不作为重点考虑参数对象.

2.2钢弹簧刚度的影响

钢弹簧的刚度作为浮置板的一项重要参数，其刚度的大小将直接影响浮置板的固有频率[1]，下面就不同的钢弹簧刚度来研究浮置板固有频率的变化.钢弹簧刚度对浮置板轨道固有频率的变化规律如图4(以钢弹簧刚度12 kN/mm为基准刚度)所示.

图4　弹簧刚度对固有频率影响变化图

如图钢弹簧刚度的降低，系统的固有频率降低比较明显.第一阶固有频率由5.260 2 Hz下降到3.047 2 Hz，下降百分比达到42.08%；第二阶固有频率由14.171 Hz下降到8.249 2 Hz，下降达到41.79%；但对于高频变化不明显，比如第十阶仅仅下降2.3%.因此降低钢弹簧刚度对于降低浮置板轨道的固有频率效果显著，尤其对于低阶频率的影响远大于高阶频率的影响，这也正是浮置板轨道减振降噪所满足的，因此在满足整体受力和位移的情况下应尽量减小钢弹簧的刚度.

2.3钢弹簧间距的影响

钢弹簧间距的变化直接影响到单位长度内钢弹簧的并联刚度[1]，同时也会影响结构的受力和位移.下面选择三种间距研究钢弹簧间距变化对轨道固有频率的影响.钢弹簧间距对浮置板轨道固有频率的变化规律如图5(以钢弹簧间距0.5 m为基准间距)所示.

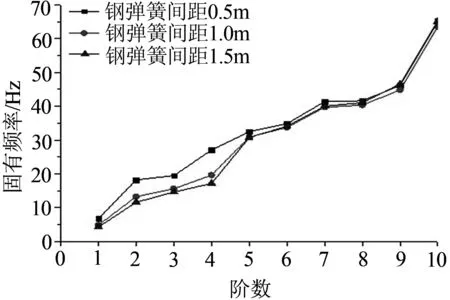
图5　弹簧间距对固有频率影响变化图

钢弹簧浮置板轨道结构的固有频率随着钢弹簧间距的增大而降低，当间距有0.5 m增加到1.5 m时，第一阶固有频率由6.7595Hz减少到4.302 2 Hz，减少百分比为36.35%，同样第二阶固有频率由18.215 Hz减少到11.617 Hz，减少了36.22%，以此类推均有减少的趋势，不过从图上可以看出，间距的变化对低频的影响大于高频的影响，和钢弹簧刚度的变化有类似的规律，而间距的变化也会降低单位刚度，因此应同时考虑钢弹簧刚度和间距对固有频率的影响，但是也必须满足受力和变形的要求.

2.4曲线半径的影响

曲线段浮置板轨道结构中，曲线半径也应该作为一个重要参数考虑.分四种情况研究半径变化对浮置板固有频率的影响.曲线半径对浮置板轨道固有频率的变化规律如图6(以曲线半径300 m为基准半径)所示.

图6　曲线半径对固有频率影响变化图

由上图可以看出随着浮置板曲线轨道半径的增加浮置板轨道的固有频率有所降低，并且对于高频的影响大于低频的影响.不过由于设计线路时，线路的走向基本已经确定，想大幅度改变曲线半径是不符合实际情况的，因为可以不作为重点考虑参数对象.

2.5浮置板弹性模量的影响

本文选取了四种浮置板轨道的弹性模量来研究对轨道固有频率的影响.浮置板弹性模量对浮置板轨道固有频率的变化规律如图7(以钢弹簧弹性模量57.5 GPa为基准弹性模量)所示.

图7　板弹性模量对固有频率影响变化图

随着浮置板弹性模量的降低，浮置板轨道的固有频率也降低.当浮置板弹性模量由57.5 GPa降低到20 GPa时，第一阶固有频率由4.308 3 Hz减小到4.293 6 Hz，减少了0.34%，第二阶固有频率由11.658 Hz减小到11.564Hz，减少了0.81%，第九阶固有频率由64.469 Hz减小到39.331 Hz，减少了36.01%，第十阶固有频率由71.747 Hz减小到55.177 Hz，减少了23.1%.因此改变浮置板的弹性模量对于高阶频率的影响大于低阶频率的影响，综上减小轨道弹性模量会降低浮置板轨道的固有频率.

2.6浮置板密度的影响

本文选取了五种不同的密度来研究对轨道固有频率的影响.浮置板密度对浮置板轨道固有频率的变化规律如图8(以浮置板密度2200kg/m3为基准密度)所示.

图8　浮置板密度对固有频率影响变化图

浮置板密度的变大，会降低轨道结构的固有频率.综合考虑可以发现，道床的密度越大轨道的固有频率越低，并且降低的百分比近似相同.

3　结论

(1)随着扣件刚度的增加，浮置板轨道的固有频率有所增大，但是增加幅度非常小，因此在进行减振降噪研究时，可不作为重要考虑的参数；

(2)随着钢弹簧刚度的降低，浮置板轨道的固有频率降低比较明显，并且对于低频的影响大于高频的影响，符合减振降噪的要求，应作为重点研究对象；

(3)随着钢弹簧间距的增加，会降低单位钢弹簧的刚度，因此会降低轨道的固有频率，并且对于低频的影响大于高频的影响，同时钢弹簧的刚度和间距是一组相关的参数量，一种参数的变化同样会

改变另外一种参数的变化，因此应综合考虑；

(4)随着曲线半径的增加，会降低轨道结构的固有频率，并且对于低频的影响大于高频的影响；

(5)随着浮置板轨道的弹性模量减少，会降低轨道的固有频率，并且对于高频的影响大于低频的影响；

(6)浮置板密度的增加会降低轨道的固有频率，并且每一阶的降低幅度近似相同；

(7)在影响浮置板固有频率的众多参数中，钢弹簧刚度和间距是影响其大小的关键参数，应作为重点参数进行研究.

综上可以看出影响轨道固有频率的参数较多，并且参数之间也有一定的关联，一个参数的改变同样会改变另外一种或多种参数的变化，因此在进行减振降噪的研究时，在满足受力和位移安全的情况下，应综合考虑每一个因素的影响，通过优化组合才能确定最佳的参数取值.

[1]王汉民.城市轨道交通浮置板轨道振动特性研究及对邻近建筑物的影响[D]. 北京：北京交通大学，2009.

[2]郭亚娟,杨绍普,郭文武.钢弹簧浮置板轨道结构的动力特性分析[J].振动、测试与诊断,2006(2):146-150.

[3]翟婉明.车辆-轨道垂向系统的统一模型及其耦合动力学原理[J].铁道学报,1992(3):10-21.

[4]耿传智,楼梦麟.浮置板轨道结构系统振动模态分析[J].同济大学学报(自然科学版),2006(9):1201-1205.

[5]张格妍车辆-浮置板轨道垂向耦合动力特性研究[D]. 北京：北京交通大学,2004.

[6]蒋崇达.内置式钢弹簧浮置板轨道动力特性分析[D]. 南昌：华东交通大学,2013.

[7]王汉民.城市轨道交通浮置板轨道振动特性研究及对邻近建筑物的影响[D]. 北京：北京交通大学,2009.

[8]丁德云,刘维宁,张宝才,等.浮置板轨道的模态分析[J].铁道学报,2008(3):61-64.

Modal Analysis of Steel Spring Floating Slab Track Structure

JIANG Alan，LI Jianmin

(School of Civil and Safety Engineering, Dalian Jiaotong University, Dalian 116028，China)

Three-dimensional modal analysis on the floating slab track is simulated by Software ANSYS. The natural frequency of the track structure under different parametersis obtained，and the influence of various parameters on the natural frequency of floating slab track is analyzed，which provides a reference for future researchers. Trough contrast analysis of the parameters，the stiffness and spacing of steel springs are very important parameters which influence the natural frequency，and should be focused on research.

floating slab track；modal analysis；natural frequency

1673- 9590(2016)05- 0089- 04

2016- 03- 21

国家自然科学基金资助项目(51508066)；大连市建委资助项目

江阿兰(1975-)，女，教授,博士，从事桥梁结构分析、损伤诊断的研究

A

E- mail:296528750@qq.com.