马斯京干法在韩庄运河洪水演算中的应用
2016-09-24刘艳亮
刘艳亮
(枣庄市岩马水库管理处,山东 枣庄 277100)
马斯京干法在韩庄运河洪水演算中的应用
刘艳亮
(枣庄市岩马水库管理处,山东枣庄277100)
韩庄运河是南四湖韩庄闸以下的泄洪通道,本次采用马斯京根法对韩庄运河河段进行河道洪水演算,将其洪水演算方案运用到实际工作中以提高预报时效和精度要求。
马斯京根法;洪水演算;流量分级;汇流曲线
韩庄运河是南四湖韩庄闸以下的泄洪通道,也是枣庄市南部的主要排水河道,全长42.5 km。该区域是暴雨集中频发地区,往往因暴雨造成较大洪水;加之上游微山湖韩庄闸泄洪,下游顶托,河道排水不畅,致使运北地区经常发生大面积洪涝灾害,故该地区历来有“洪水走廊”之称。
1 韩庄运河洪水演算方案
1.1马斯京根法的原理及演算公式
本法假定在涨、落水阶段,河段中的水面是直线,流量沿程是直线变化的,把洪水期河段中的蓄水量分为两部分,即平行于河底的直线以下部分称柱蓄和在该直线与实际水面线间的部分称楔蓄。根据以上假定原理,马斯京根推求的洪水演算公式为:

式中:I为河段上段面入流量;O为河段下段面出流量,脚码1、2表示时段初、末时刻;K为槽蓄系数,是线性槽蓄关系的斜率,具有时间因次;x为流量比重因子,它反映楔蓄的大小,且0≤x≤0.5,C0、C1、C2是马斯京根法参数K和X的函数,其和等于1。
1.2方案研制步骤
1)1995年韩庄运河河道治理后到2015年根据水文资料记录主要有1998年、2003年、2004年和2005年韩庄闸泄洪四次洪水过程。2)分别绘制各场次实测洪水水位流量过程线。3)通过水位流量过程线分析各场次洪水,选择区间来水较小,韩庄闸站、台儿庄闸站上下游相应、峰形完整的洪水过程作为推求公式的依据。4)通过对以上4个场次的洪水对比分析,选取较有代表性的2005年9月19日~10月11日的洪水过程,该洪水过程较为典型符合上述特征满足推算要求。
1.3马斯京根法参数的确定方法
1)计算时段△t值的选取。按照韩庄水文站和台儿庄闸水文站的洪水资料,韩庄水文站流量为I,台儿庄闸站的出流量Q;区间入流q主要来自峄城大沙河;韩庄闸至台儿庄闸水文站约35 km,可以取△t=6 h。根据本次研制方案要求,分别采用△t=6 h、△t=2 h试算,进行对比分析。
2)参数x、K的确定。本次演算方案研制对x、K采用试算图解的方法推求。
通过假定不同数值的x进行试算,点绘W/ ⊿t~Q’关系曲线,经过多次试算,无法确定使W= f(Q’)呈单一关系的较理想的x值(流量比重因数)。因此,根据绘制曲线点据分布情况将流量分级试算x,K值。通过对2005年9月19日~10月11日洪水进行流量分级选取不同等级的流量Q;试算X值然后得马斯京根系数如表1。
根据流域特征及历年洪水资料,建议在韩庄至台儿庄河段用马斯京根法进行洪水演算时取△t=6 h比较符合实际情况。
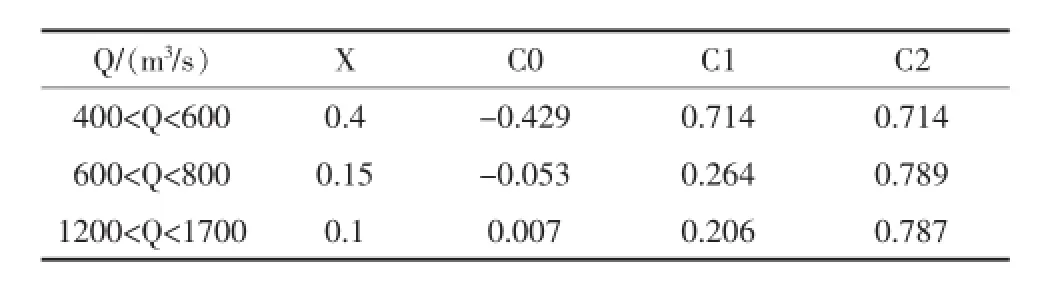
表1 各流量级马斯京根系数
1.4汇流曲线推算及误差分析
汇流曲线推算成果详见表2。选取2005年9 月25日至28日的一次洪水过程做精度分析与实测流量进行对照,分析详见表3,相对误差均在±10%以内,因此用马斯京根法推流演算与实测结果较为一致。该方法可作为实时洪水预报的有效方法。
2 结语
在挑选洪水和试算过程中发现,当闸门处于敞泄状态时,河道洪水特征基本符合马斯京根假定原理的要求,此时能够较好的建立W/⊿t~Q’单一关系,从而确定参数x、K,进一步推求出演算公式,且在分析洪水时具有较高的精度。在实际预报中需根据河道洪水的不同量级采用与之对应的参数合理使用,以达到较好的预报精度。

表2 汇流曲线推算成果 m3/s

表3 马斯京根法推流演算成果
[1]袁作新.流域水文模型.北京∶水利水电出版社,1990.
[2]芮孝芳.水文学原理.北京∶中国水利水电出版社,2004.
(责任编辑赵其芬)
TV87
B
1009-6159(2016)-08-0052-02
2016-03-17
刘艳亮(1979—),男,工程师
