基于距离检验的江苏省城市商品房价格回归模型分析
2016-09-24胡江
胡江
(徐州工程学院数学与物理科学学院,江苏 徐州 221008)
基于距离检验的江苏省城市商品房价格回归模型分析
胡江
(徐州工程学院数学与物理科学学院,江苏 徐州 221008)
随着我国经济的不断发展,我国城市商品房的建设的脚步也不断加快,商品房价格也几经起伏,因此,房价也成了现如今人们关注的焦点。江苏作为经济大省,其商品房价格有着更突出的代表性。本文通过2002年到2013年的江苏省城市商品房销售面积、江苏省人均GDP、城市居民消费价格指数这三个主要因素对江苏省城市商品房平均销售价格变动的影响来分析研究江苏省城市商品房的价格模型。我们运用线性回归模型和非线性回归模型对相关数据进行实际模拟,再运用拟合效果可视化,并运用了Pena距离和Cook距离这两种距离分析法来判断模型的拟合效果,然后将这两个模型进行比较,最后得出了非线性模型对于该数据的拟合效果较为理想。
城市商品房;回归分析;商品房价格指数;异常值检验;距离判别
在以往的回归分析中,通常采用的是显著性检验、拟合效果图等来检验模型的有效性,本文在以上方法的基础上更进一步地引进了Pena距离和Cook距离这两种距离检验。通过这两种距离的定量计算,我们不但可以判断出离群点,还可以判断是否为强影响点,从而在检验模型的拟合性上得到了更好的效果。
一、数据整理
对商品房价格影响的因素很多,根据主成分分析,我们只选取了三个重要指标:商品房销售面积:X1,人均GDP:X2,城市居民消费价格指数:X3。
对2002年到2013年江苏省城市商品房价格的相关数据整理如表1。其中商品房本年销售价格:Y。
(一)商品房价格预测分析的线性回归模型假设
因为对因变量的影响因素超过了一个,要确定它们之间的关系十分困难,所以借由已有的关于城市商品价格的研究分析,我们假定因变量商品房销售价格和商品房销售面积、人均GDP和城市居民消费价格指数这三个变量满足线性回归模型:
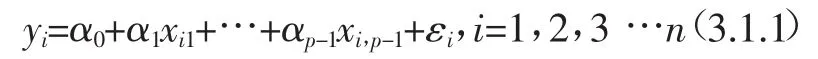
上式中因变量是yi,自变量是为随机误差。
1.回归分析检验
利用R软件对样本数据进行回归分析,从输出的结果我们可以建立回归方程:y=-3845+0.11x1+0.08x2+ 4.74x3,并得出变量x1,x2,x3的t统计量的估计值分别是1.794、7.319、1.058。从解释变量的方面来判断显著性:从对应的P值我们可以看出,解释变量在显著性水平0.05下很明显不为0,通过显著性检验。我们进一步看出剩余方差估计值σ^2=280.22,从方程拟合度方面来观察:根据拟合优度和修正的拟合优度,尤其是修正的拟合优度= 0.9752,可以看出方程拟合程度比较理想。对方程进行显著性检验,其F统计量的P值0.0000002589远远小于0.05,从显著性水平看出线性模型拟合的效果比较理想。但进一步地运用R软件将样本数据进行图形展示,发现有三处突兀点,得出的拟合效果图并不理想。
2.Pena距离及Cook距离的分析检验
为了进一步确定模型的拟合效果,我们引入Pena距离和Cook距离这两个检验异常点的统计量。我们根据已有的线性回归模型的Pena距离的计算公式对各个点Pena距离进行详细计算。计算出各点的Pena距离如下表2。运用R软件计算出个点的Cook距离如下表3所示。
经过以上的研究分析,我们可以看出该模型的拟合具有三个明显的异常值点,占样本比重25%,拟合效果并不太理想。这三个异常点分别代表的2008年、2011年、2013年的样本数据。我们查询资料可以发现:2008年中国人口结构出现拐点,国际经济危机出现。2011年房产企业品牌化使得房产业绩增长,市场份额提高。行业集中度进一步提高,土地出让总量提高。2013年政府加快推进商品房市场化的进程,相关部门对房地产的关注持续加强,政府房地产市场调控力度加大。这些因素严重影响了房价的三个因素,进而影响了房价。
由以上实际与理论相结合的分析,我们可以看出线性模型的拟合不是十分理想,以往的线性回归检验效果不明显。我们再进一步地进行模型假设,从而寻找更加适合的模型来预测商品房价格。
(二)商品房价格预测分析的非线性模型假设
我们假定所列出的影响江苏省城市商品房价格的相关因素的数据满足非线性回归模型,那么它可以表达成
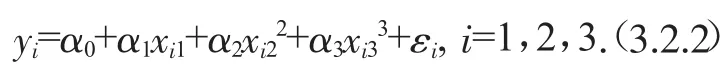
1.回归分析检验
将样本数据导入R软件。根据假设我们运用R软件对样本数据进行回归分析。并对运行结果按照解释变量、拟合优度和方程整体优度三个方面进行详细的研究判断,从而确定非线性模型的表达式。根据输出结果,我们可以建立如下的回归模型:
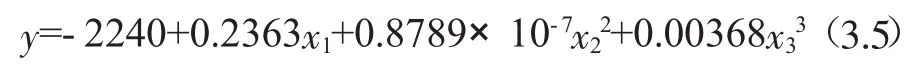

表2 线性模型下各点的Pena距离

表3 线性模型下各点的Cook距离
2.Pena距离及Cook距离的分析检验
为了能够更加准确地判断该模型的拟合效果,我们进一步计算Pena距离和Cook距离这两个检验异常点的统计量。根据已有的非线性模型下的Pena距离的公式,我们计算出各点的Pena距离如下表4。

表4 非线性回归模型下的Pena距离
用R软件根据上述非线性回归模型计算出各点的Cook距离如下表5。

表5 非线性回归模型下的Cook距离
从上面表3-12的Pena距离的结果中,我们可以很明显地看出第12号点数值存在明显异常。然而从表3-13中我们很难明显发现异常值,经过认真比较后我们发现,12号点是高杠杆异常点,而对于高杠杆异常点Pena距离比Cook距离检验效果更好,符合理论结果。因此,我们断定12号点是异常点,但我们从Pena距离值看出,它对模型的偏离程度并不大,属于弱异常点。
由以上分析我们发现:在线性模型的回归分析中,各分析成分大都与模型吻合;但从拟合效果图来看,有3处突兀较显著;进一步运用Pena和Cook距离进行量化判断,则出现了三个点严重脱离模型曲线,占整体数据的25%,拟合效果大打折扣。
从非线性回归模型的回归分析出的结果,可以看出模型中各个相关指标都十分正常,拟合的效果图也大体符合模型规律,运用Pena距离和Cook距离对该模型就行异常值量化检验。结果发现,只有第12号点存在些许异常,偏差也并不太明显,模型与数据点基本都吻合。因此,我们认为商品房价格预测的模型如下:
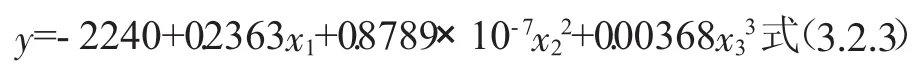
这一模型能够更为准确地描述商品房价格走向。
[1]韦博成,林金官,解锋昌.统计诊断[M].北京:高等教育出版社,2009.
[2]胡江.基于Pena距离的几种回归模型的影响分析[D].东南大学,2012.
[3]王新洲.非线性模型参数估计理论与应用[M].武汉:武汉大学出版社,2002.
G718.5
A
1673-0046(2016)7-0010-02
