Plate/shell topological optimization subjected to linear buckling constraints by adopting composite exponential filtering function

Hong-Ling Ye·Wei-Wei Wang·Ning Chen·Yun-Kang Sui



RESEARCH PAPER

Plate/shell topological optimization subjected to linear buckling constraints by adopting composite exponential filtering function

Hong-Ling Ye1·Wei-Wei Wang1·Ning Chen1·Yun-Kang Sui1

In this paper，a model of topology optimization with linear buckling constraints is established based on an independent and continuous mapping method to minimize the plate/shell structure weight.A composite exponential function（CEF）is selected as filtering functions for element weight，theelementstiffnessmatrixandtheelementgeometricstiffnessmatrix，whichrecognizethedesignvariables，and to implement the changing process of design variables from“discrete”to“continuous”and back to“discrete”.The buckling constraints are approximated as explicit formulations based on theTaylor expansion and the filtering function.The optimization model is transformed to dual programming and solved by the dual sequence quadratic programming algorithm.Finally，threenumericalexampleswithpowerfunction and CEF as filter function are analyzed and discussed to demonstrate the feasibility and efficiency of the proposed method.

Topological optimization·Plate/shell structure·Linear buckling constraint·Independent continuous and mapping（ICM）method·Filter function

1 Introduction

Structural topology optimization is to find optimal material layout within a given design space，for a given set of loads and boundary conditions such that the resulting layout meets a prescribed set of performance targets.The essence of topology optimization lies in searching for the optimum path of transferring loads，therefore the computational results of topology optimization are usually more attractive and more challenging than the results of crosssectional and shape optimization.In the last decades，since the landmark paper of Bendsøe and Kikuchi［1］，numerical methods for topology optimization of continuum structures have been developed quickly in application［2-4］.The classical methods include the homogenization method［5，6］，the variable density method（including solid isotropic material with penalization model（SIMP）and rational approximation of material properties（RAMP）interpolation model）［7-10］，evolutionarystructuraloptimization（ESO）［11-13］，levelset method［14-16］，and so on.

The plate/shell structure is popular for lightweight constructions in national defense and civil industries.However，it is shown from both research literature and industrial applications that plate/shell structures are prone to buckle.As buckling affects the security of the whole structure，it is necessary to address the structural stability during structure design.Buckling topology optimization of plate/shell is to find optimal material layout of plate/shell structure that meets the buckling requirements.Although buckling topology optimization is only in the phase of conceptual design in engineering，the optimal results will impact the performance of the final structure significantly.Compared with static topology optimization，buckling topology optimization is more complicated，and there are few investigations up till now.In 1995，linear buckling topology optimization of two-dimensional structures had been studied by Neves et al.［17］，the optimization results lay the foundations for the non-linear buckling optimization.Meanwhile，Seo［18］studied the topology optimization of inner-wall stiffener of cylindrical containers.The reciprocal of critical buckling load was adopted as an objective function，and the totalmass of stiffener was constrained to a prescribed value. Later，Neves et al.［19］presented a two-scale asymptotic method for the linearized elastic stability analysis.Topology optimization of the periodic microstructures is carried out based on the local buckling instabilities in the periodic boundary conditions（PBC）.Combining the linearized elastic buckling model with the inverse homogenization and an eigenvalue buckling analysis with Floquet-bloch wave theory［20］，the minimum critical buckling strain is obtained andmaximizedwiththePBChavingaconstantvolumefraction of materials.In 2002，Ramm et al.［21，22］constructed the topology optimization model with linear buckling constraints based on the SIMP method to study the influence of geometrical nonlinear behavior to topology optimization design.In 2004，the shell’s topological optimization under linearbucklingresponseusingSIMPpower-lawpenalization ofstiffnesswasgiventoachievethediscretetopology［23］.In 2009，Lund［24-26］studiedthebucklingtopology optimization of laminated multi-material composite shell structures by introducing interpolation functions，which is from the SIMP approach.In 2012，Browne［27］studied the method of solving the large-scale quadratic programming problem，and the method is applied to the topology optimization problem using compliance and buckling as constraints with the minimum structural weight as objective.In 2013，Lindgaard［28］studiedthestaticgeometrynonlinearstructuretopologyoptimizationofinstabilitytomaximizethebucklingcriticalload.

Up till now，different optimization methods have been used to solve the buckling structure topology optimization problems，however，there is no uniform valid method to deal withthebucklingtopologyoptimizationofplate/shell.Thisis so since building the buckling topology optimization model is more complex and difficult than static topology optimization，and calculations for sensitive analysis are enormous.

In this paper，we investigate buckling topology optimization based on independent，continuous and mapping（ICM）method，proposed by Sui［29］for skeleton and continuum structural topology optimization in 1996.The topological variables are independent of design variables such as sectional sizes，geometrical shape，density or Young’s modulus of material.Filter functions are used to map the changing process of topological design variables from“discrete”to“continuous”and back to“discrete”.The smooth model for structural topology optimization is established and solved by the traditional algorithms in mathematical programming. The ICM method has been mainly used to study static and dynamic topology optimization［30-32］.We extend this method and do in depth research for the buckling problem. A model of topology optimization for the lightest plate/shell structures with the critical buckling load constraints is constructed.Usually，a power function（PF）is selected as the filter function in the past，and we select a composite exponential function（CEF）as the filtering function to complete thechangingprocessofdesignvariables.Theoptimalresults withtwodifferentfilterfunctionsarecomparedbynumerical examples.

This paper is organized as follows.In Sect.2，a buckling topology optimization model of plate/shell structure based on the ICM method is established.In Sect.3，a strategy for solving the buckling optimization model is introduced.An optimal algorithm to solve the mathematical optimization problem is given.In Sect.4，the program flow of the optimization algorithm is charted.Three numerical simulations are presented in Sect.5.In Sect.6，conclusions are given.

2 Establishment of linear buckling topology optimization model

2.1 Linear buckling analysis of plate/shell structures

Structural buckling widely exists in practical engineering structure.Buckling is a mathematical instability，leading to a failure mode.As the applied load is increased on a structure by a small amount beyond the critical load，the structure deformsintoabuckledconfiguration.Furtherloadwillcause significant and somewhat unpredictable deformations，possibly leading to complete loss of the structural load-carrying capacity.Theinterpretationofthisresultisthatfor P＜Pcrj，the structure remains stable.For P＞Pcrj，the structure is unstable and buckles.Pcrjis the critical load for buckling. Usually，oncetheformofstructureisestablished，itsbuckling will have a variety of modes and multiple critical loads. The structure will not work before the mode reaches higherorder buckling mode，so we just care about the first-order critical load of buckling mode.In this paper，the linear elastic and pre-buckling of continuum structure is considered. Assuming the structure to be perfect with no geometrical imperfections，stresses are proportional to the loads，i.e.，stress stiffness depends linearly on the load，displacements at the buckling configuration are small，and the load is independent of the displacements.The linear buckling problem can be represented as［28，29］

where K and G denote the structural stiffness matrix and geometric stiffness matrix，respectively，λjis the j-th eigenvalue，i.e.，buckling critical load factor and ujdescribes the corresponding eigenvector，j denotes the j-th order of the modal.

2.2 Description of the filter function based on the ICM method

FilterfunctionisthekeystrategyoftheICMmethod.Itidentifies thecorresponding element or subdomains of geometricquantityorphysicalquantity，suchastheelementweight，the element stiffness matrix，and the element geometric stiffness matrix.Discrete design variables can be mapped to continuous variables by filter function and inversed back to discrete variables.For the buckling topology optimization model，we define element weight，the element stiffness matrix，and the element geometric stiffness matrix as follows

where tiis the topology variable value of the i-th element. wi，ki，gidenotes the element weight，stiffness matrix，and geometric stiffness matrix of i-th element in the optimal process，respectively.Andw0i，k0i，g0irepresenttheinitialelement weight，stiffnessmatrix，andgeometric stiffnessmatrix ofthei-thelement，respectively.fw（ti），fk（ti），and fg（ti）are the filter functions of the element weight，element stiffness matrix，and the element geometric stiffness matrix.

In addition，the element weight，element stiffness matrix，element geometry stiffness matrix，and element quality matrix are changed by taking advantage of filter functions. Thesephysicalquantitiesofeveryelementchangealotwhen the structural topology changes，and then the filter functions in the formulation can lead to convergence.Furthermore，filter functions influence the speed of convergence and the stability of the solution of the optimal process.

Several types of filter function are suggested in the ICM method［33］.Among which，the PF is used frequently as follows

Here，α is a given positive constant.

Now，we introduce a new filter function-CEF to take the place of PF，and it is as follows

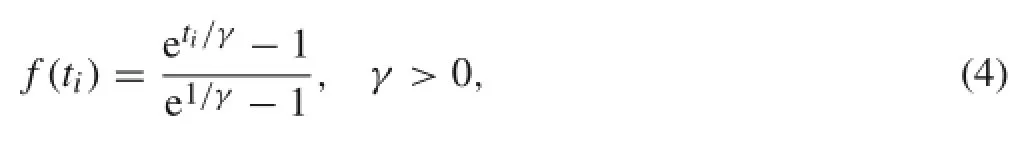
where γ is a given positive constant.In Sect.5，the performances of the two types of filter function are compared.

From Eqs.（2），（3），and（4），the specific expressions of PF and CEF in the model of buckling topology optimization are given:

It should be pointed out that these parameters of filter functions can be determined by using the least squares method or numerical experiments，see Refs.［29-31］.

2.3 Mathematical model of buckling topology optimization

BasedontheICMmethod，theoptimalmodeltominimizethe structural weight subjected to the linear buckling constraints is as followscrjis the lower limit buckling critical load，and J and N denote the totalnumber ofthebucklingmodesandnumberofelements.

The relationship between critical load and external load P can be expressed as

where t denotes the vector of topological design variables，W is the structural weight，and wiis the element weight of structure，Pcrjpresents the critical buckling load，P

Then the buckling critical load factor is used as constraints in the optimal model.The buckling topology optimal model（6）can be transformed as follows

Inordertosolvetheoptimalmodel，thereciprocaloffilter function with stiffness matrix is used as a design variable as follows

Therefore，the topological design variable is expressed as

Then Eq.（2）can be transformed into Eq.（11）

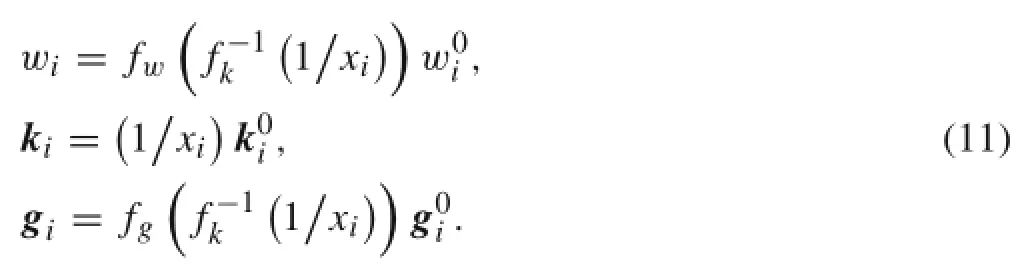
Withtheintroductionoffilteringfunctionsandthereciprocal of filter function of stiffness matrix，the optimization model（8）is written as

3 Strategy for solving the buckling optimization model

3.1 Design sensitivity analysis

To estimate the design sensitivity，we have to consider the derivative of the eigenvalue in Eq.（1）.The eigenvalues can be expressed using the Rayleigh quotient:

The derivative of the eigenvalue is given as follows

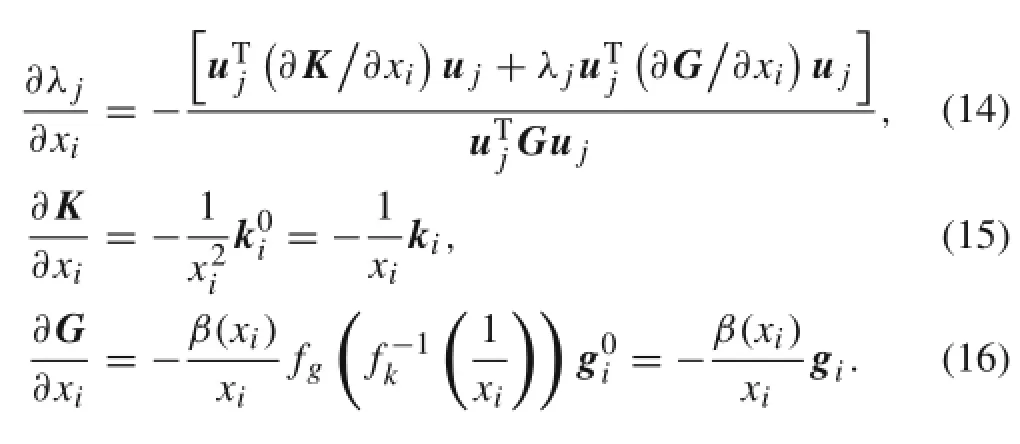
βican be obtained according to different type of filter function.When PF is selected as filter function，

And CEF acts as filter function，

Therefore，Eq.（14）is deduced as

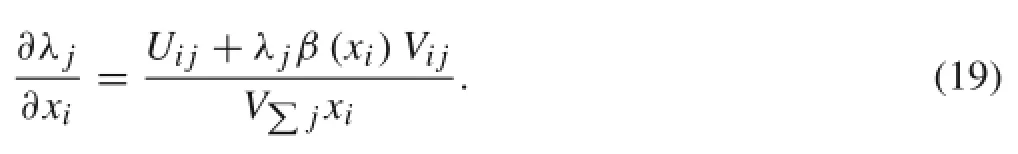
3.2 Explicit approximation of buckling constraints

As the constraint is implicit about design variables，we make it explicit by using the first order Taylor expansion:

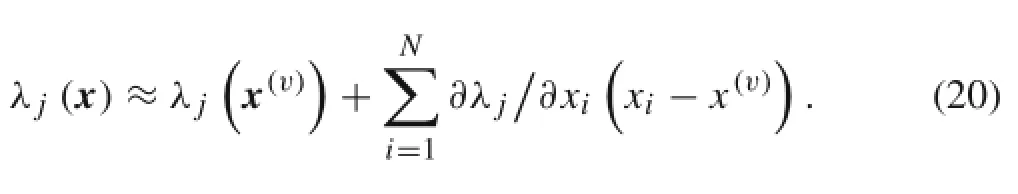
Here，the superscript v is the number of iterations.Take Eq.（20）into Eq.（21），we have

Then the buckling constraints in model（12）can be expressed as

We set

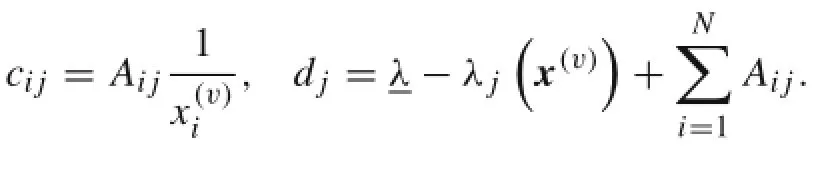
Sothebucklingconstraintscanbesimplifiedtothefollowing form

3.3 The standardization of the objective function

Inordertoobtainanexplicitobjective，thesecond-orderTaylorexpansionisused.WhenPFisselectedasafilterfunction，the structural weight can be written

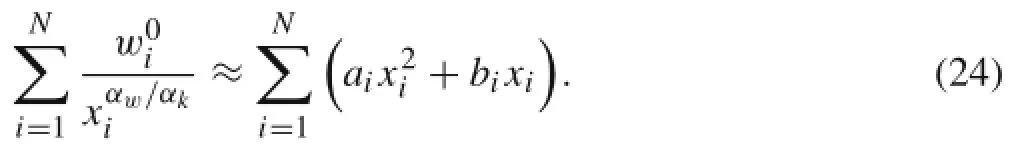
Here，

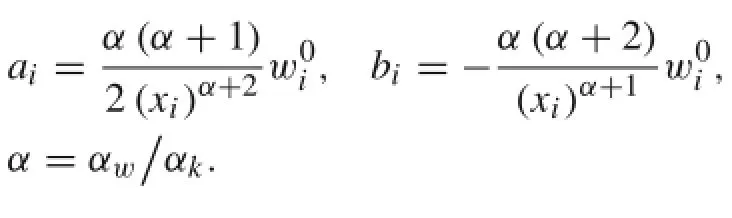
When CEF acts as filter function，the structural weight can be written

where，

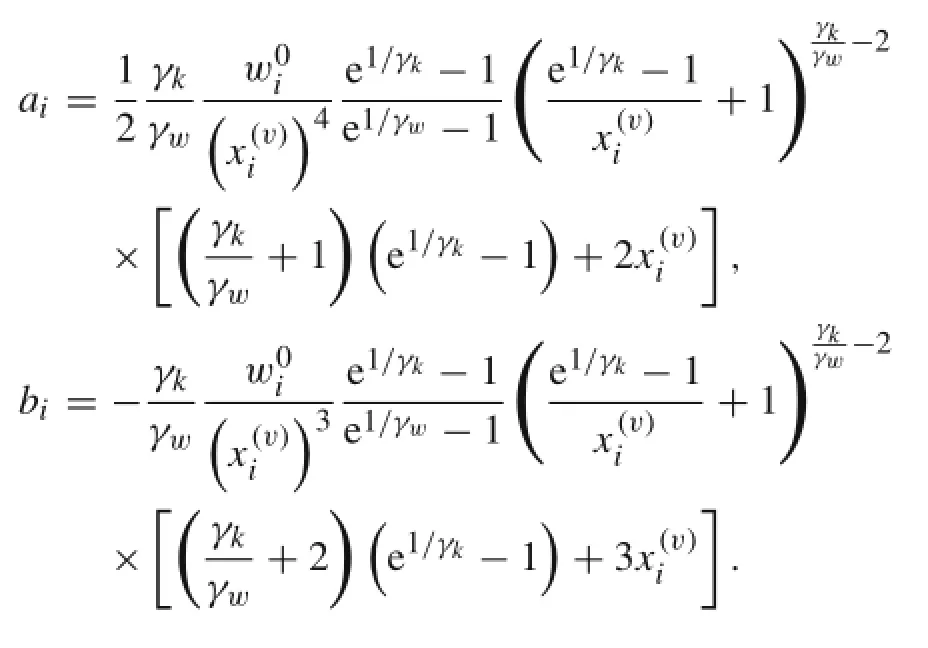
Therefore，the standard quadratic programming model for Eq.（12）can be obtained as follows

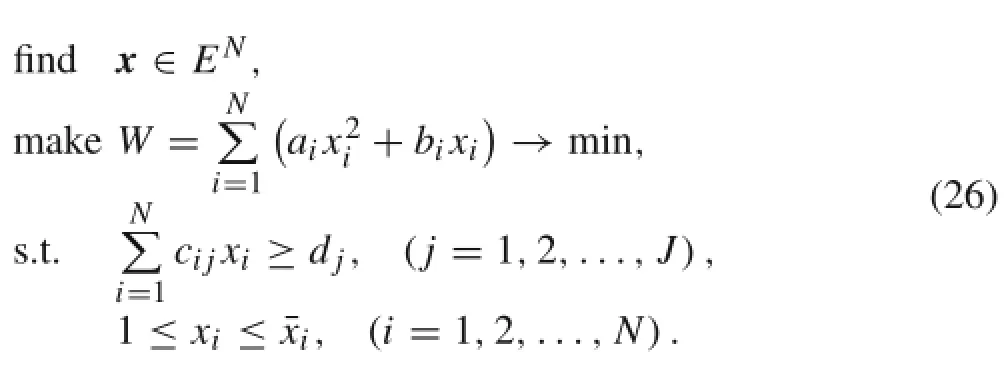
3.4 Solution of the optimization model

As the number of design variables is much bigger than that of the constraints，we deduce the dual model to decrease the number of design variables as follows in order to reduce the amount of calculation.

where z isthedesignvariablevectorofthedualmodel，Φ（z）is the objective function，and

In this paper，the convergence criterion is chosen as follows

?and?are the current iteration and the previous iteration of structural weight.ε is the convergence precision，ε=0.001.

3.5 Discrete degree of topological design variables

In order to measure the discrete degree of topological design variables，we use Mnd［34］as a criterion，and it is given

where Tiisthetopologicalvariablevalueforthei-thelement and N isthetotalnumberoftheelements.FollowingEq.（29），ifthetopologicalvariablevalueis0or1，then Mndis0；ifthe topological variable values is 0.5，then Mndis 1.The closer the topological variable value to 0 or 1，the smaller is the value of Mndand the better the optimal result.

4 Program flow of optimization algorithm

The numerical procedures are developed by the PCL toolkit in the MSC.Patran software platform.We use MSC.Nastran toanalyzethenumericalsolutionofEq.（1）.Thecorresponding program flow as shown below

Step 1 Build finite element model by using MSC.Patran；

Step2Inputinitialoptimalparametersandsetupoptimal model；

Step 3 Make buckling analysis by using MSC.Nastran；

Step 4 Calculate and extract the critical buckling factor and strain energy；

Step 5 Input parameters of the optimal algorithm；

Step6Solvethedualoptimizationmodel（27）bythedual sequence quadratic programming（DSQP）；

Step 7 Judge convergence of the optimal results.If the structural weight satisfies the formula（28），then the program is terminated.Otherwise，update design variables x and topology design variables t，then go to step3.

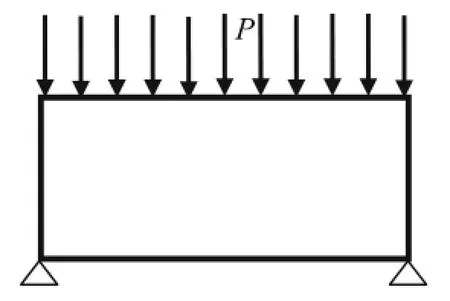
Fig.1 Base structure

Fig.2 Topology configuration with CEF filter function

Fig.3 Topology configuration with PF filter function in Ref.［34］

Fig.4 Iterative history curve of critical buckling load

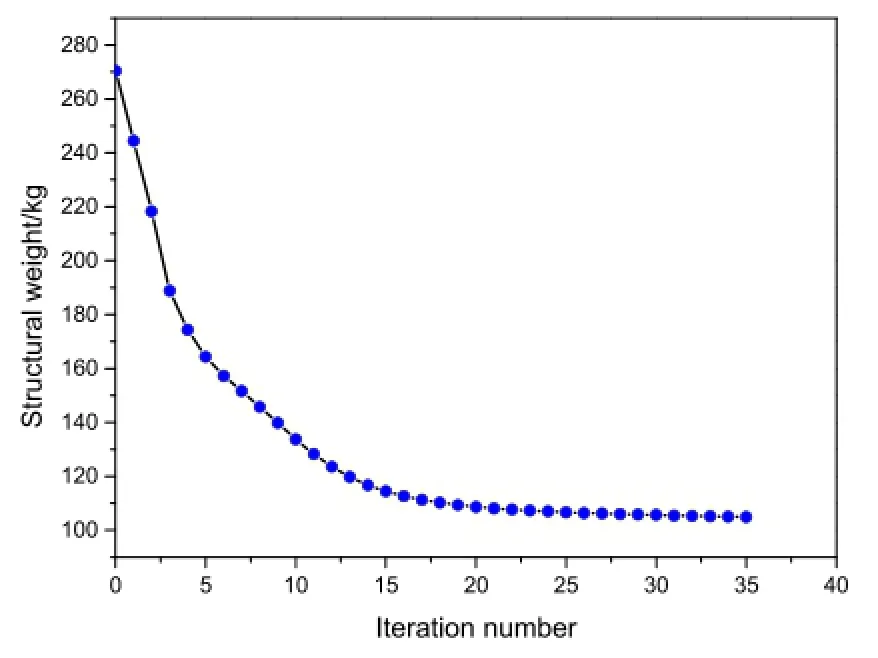
Fig.5 Iterative history curve of structural weight

5 Numerical examples

In this section，three examples of topology optimization of single material plate/shell structures are given.All the material is isotropic with Young’s modulus E=68890MPa，Poisson’s ratio μ=0.3.In the initial design，the available material is uniformly distributed over the admissible design domain.The structures are meshed by four-node 2D plate/shell finite elements.The specific boundary condition and force form are shown in the following three examples.

Example 1 As shown in Fig.1，the base structure is a plane elastic body with size 520×260×2mm3，and mass density ρ=1.0×10-3kg/mm3.The distributed compression load atthetopedgeis100N/mm.Twocornersofthebottomedge arefixed.Thebucklingconstraintvalueis100NinRef.［34］. Theregionwhichincludingtheabovetwolayersoftheunitis a non-design and should be maintained.The base structure’s weight is 0.73 kg.

The topology configuration of the structure with CEF filter function is given in Fig.2.It is similar to the topology configuration with PF as in Ref.［34］as shown in Fig.3.The iterative history curve of buckling load and structural weight are shown in Figs.4 and 5.The optimal structural weight with CEF is 104.808 kg and the iterative number is 36，as the optimal structural weight with PF is 115.756 kg and the iterative number is 51.From the point view of structural weight and iteration，the optimal results with CEF is better that of PF.

Example 2 As shown in Fig.6，the base structure is a plane elastic body and the mass density is ρ=2.7×103kg/m3. The forces P=15000 N are located on the midpoint of the top and bottom boundary.Four corners of the structure are fixed.The base structure’s weight is 0.73 kg.

After finite element analysis，the first-order buckling load factor of the structure is λ1=0.0533.The critical buckling load is 1600 N，and the buckling load 1300 N is defined as constraint value.

Thetopologyconfigurationsofthestructurewithdifferent filterfunctions beforeand after discretionaregiven inFig.7. In addition，the first-order buckling modal of optimal structure is computed as shown in Fig.8.The iterative history of buckling load and structural weight with different filter functions are depicted in Figs.9 and 10.We can see that the critical buckling loads of the optimal structures satisfy the buckling constraint.From Fig.10，we can see a clear differ-ence with PF and CEF in the structural weight and iterative number.The optimal structural weight with CEF is lighter and the number of iterations is less than that of PF.

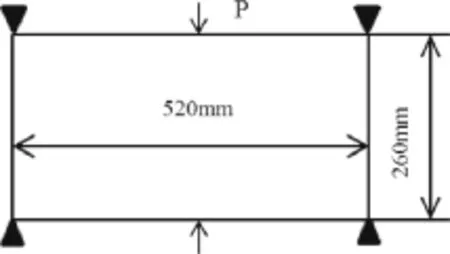
Fig.6 Base structure

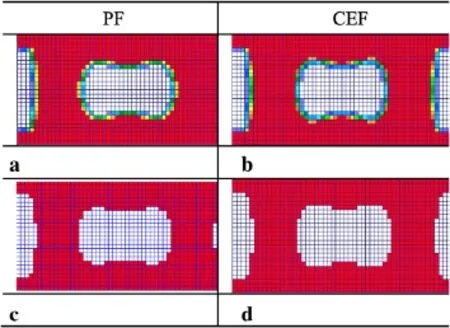
Fig.7 Topology configuration with different filter functions before and after discretion.a and b before discretion with PF and CEF，c and d after discretion with PF and CEF

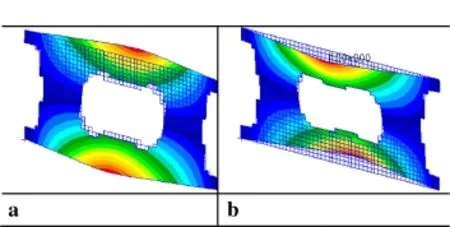
Fig.8 The first-order buckling modal of optimal structure with different filter function.a PF.b CEF

Fig.9 Iterative history of the buckling load with different filter functions

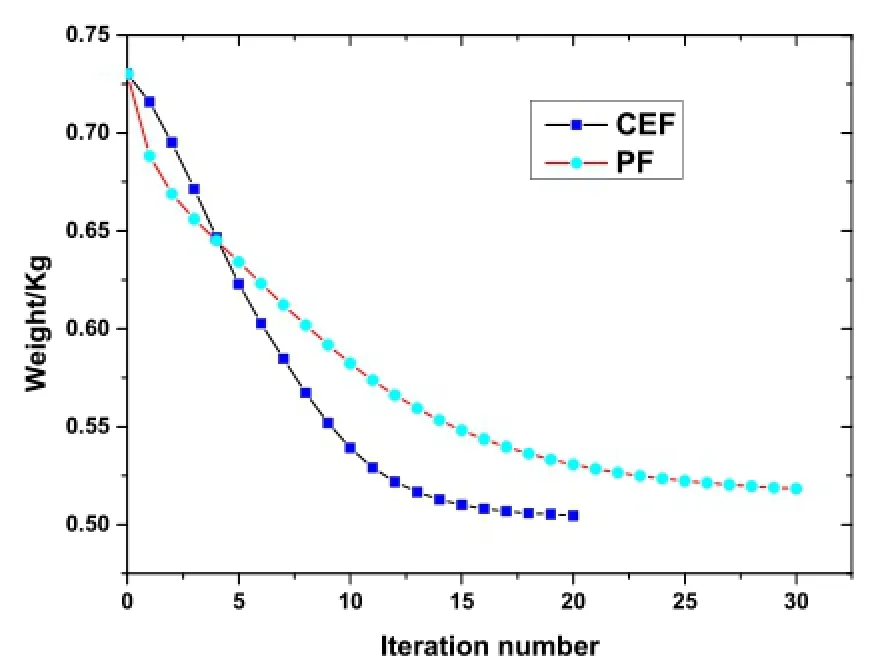
Fig.10 Iterative history of structural weight with different filter functions

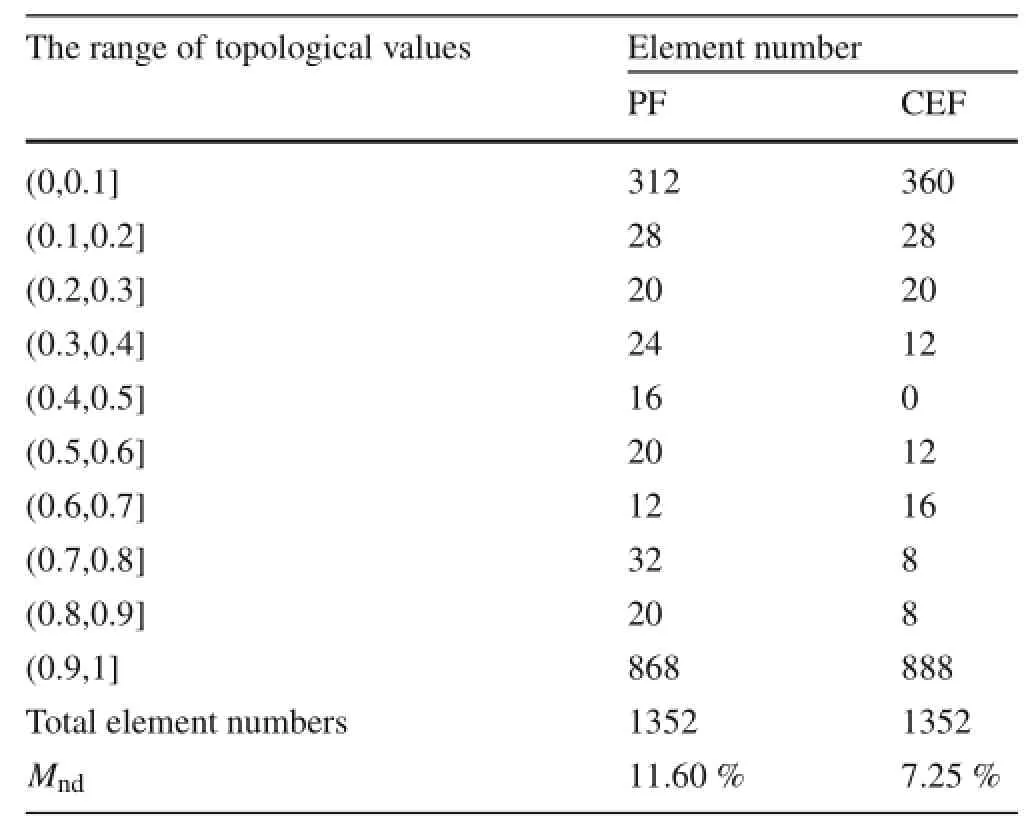
Table 1 Distribution of topological design variables

Thedistributionsoftopologicaldesignvariablesarelisted in Table 1.The discretization of topological design variables is evaluated by using Mnd.We can find that Mndwith PF and CEF are 11.60%and 7.25%.Therefore，the optimal result with CEF is better than that of PF from the view of discretization of topological design variables.

Example 3 AsshowninFig.11，thebasestructureisapartof the cylindrical shell，the generatrix is 260 mm，arc length is 520mm，andtheradiusis5000mm.Theforce P=15000N is located on the center of the cylindrical shell along the radial direction.After finite element analysis，the first-order buckling load factor of the structure is λ1=0.00325.The criticalbucklingloadis48.7N，andthecriticalbucklingload 40 N is defined as the buckling constraint value.

Fig.11 Base structure

The intermediate results and optimal topology configuration of the structure with different filter functions are indicated in Fig.12.The iterative history curve of buckling load and structural weight with PF and CEF is given in Figs.13 and 14.The performances of topological optimization with different filter functions are given in Table 2. From Fig.13，we get that the optimal structure with PF and CEF all satisfy the buckling constraint.The optimal structural weight with CEF is lighter than that of PF as shown in Fig.14.

Fromtheabovethreeexamples，wecanseethattheobjective（weight）with CEF is apparent lighter than that of PF. We can also find that the optimal result with CEF has the best performance from the point of view of iterative number.

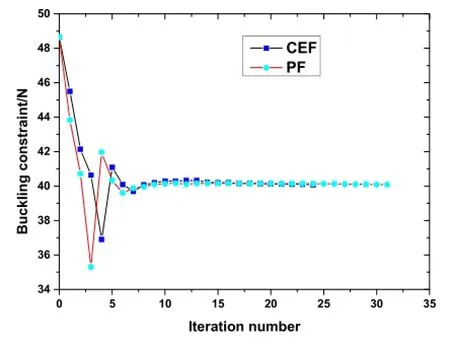
Fig.13 Iterative history of the buckling load with different filter functions

The distribution of optimal topological values show that the percentages of Mndwith CEF is lower than that of PF，so the CEF filter function has the best performance from the viewpoint of discreteness.

Fig.12 The intermediate results and optimal topology configuration of the structure with different filter functions.a The intermediate optimal results with PF.b The intermediate optimal results with CEF

6 Conclusion

In this paper，a buckling topological optimal model of plate/shellstructureisestablishedbasedontheICMmethod.CEF is selected as a filter function to recognize the design variables，as well as to implement the changing process of design variables from“discrete”to“continuous”and back to“discrete”.Explicit formulations of buckling constraints are given based on two different filter functions，first-order Taylor series expansion by extracting structural strain and structural kinetic energy from the results of structural modal analysis.The program based on DSQP for solving the optimal model is developed on the platform of MSC.Patran& Nastran.Three numerical examples of continuum structure show that clear and stable configurations can be obtained by using the ICM method.We also find that configurations computed with PF and CEF are similar.But we can see that the optimal result with CEF has the better performance from thepointofviewofoptimalobjective，iterativenumbers，and discrete degree.

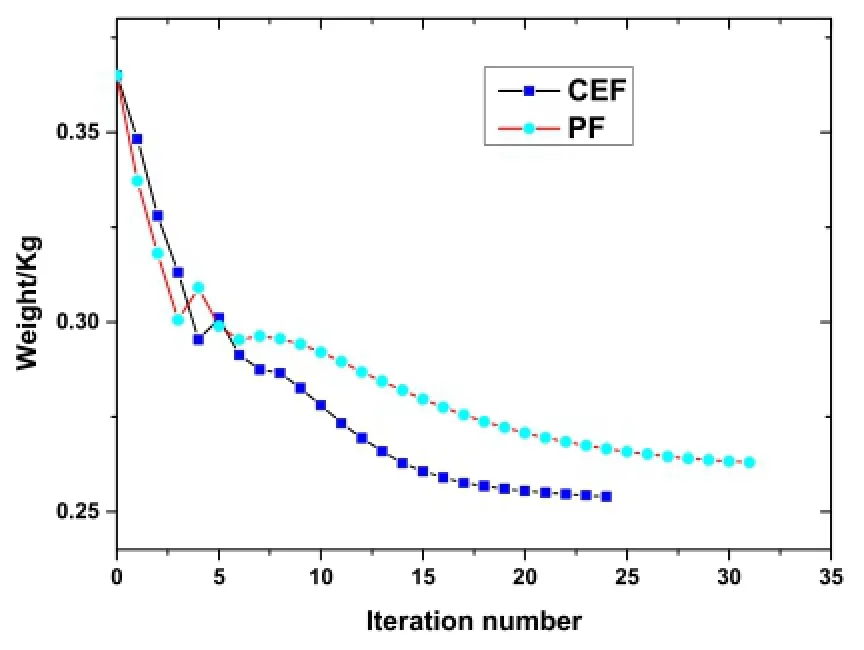
Fig.14 Iterative history of structural weight with different filter functions

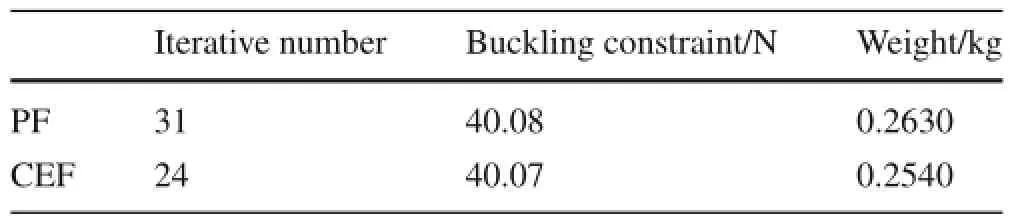
Table 2 Optimal results with different filter functions

AcknowledgmentsThe project was supported by the National Natural Science Foundation of China（Grants 11072009，111720131）.

OpenAccessThisarticleisdistributedunderthetermsoftheCreative Commons Attribution 4.0 International License（http://creativecomm ons.org/licenses/by/4.0/），which permits unrestricted use，distribution，and reproduction in any medium，provided you give appropriate credit to the original author（s）and the source，provide a link to the Creative Commons license，and indicate if changes were made.

References

1.Bendsøe，M.P.，Kikuchi，N.:Generating optimal topologies in structural design using a homogenization method.Comput.Methods Appl.Mech.Eng.71，197-224（1988）

2.Eschenauer，H.A.，Olhoff，N.:Topologyoptimizationofcontinuum structures:A review.Appl.Mech.Rev.54，331-390（2001）

3.Deaton，J.D.，Grandhi，R.V.:A survey of structural and multidisciplinary continuum topology optimization:Post 2000.Struct. Multidiscip.Optim.49，1-38（2014）

4.Rozvany，G.I.N.:Aims，scope，methods，history and unified terminology of computer-aided topology optimization in structuralmechanics.Struct.Multidiscip.Optim.21，90-108（2001）

5.Bendsøe，M.P.，Sigmund，O.:Topology Optimization:Theory，Methods and Applications，2nd edn.Springer，Berlin（2003）

6.Hassani，B.，Hinton，E.:A review of homogenization and topologyoptimization-homogenizationtheoryformediawithperiodic structure.Comput.Struct.69，707-756（1998）

7.Cao，M.J.，Ma，H.T.，Wei，P.:A novel robust design method for improving stability of optimized structures.Acta Mech.Sin.31，104-111（2015）

8.Zhang，H.，Liu，S.T.，Zhang，X.:Topologyoptimizationof3Dstructures with design-dependent loads.Acta Mech.Sin.26，767-775（2010）

9.Sigmund，O.:A99linetopologyoptimizationcodewritteninMatlab.Struct.Multidiscip.Optim.21，120-127（2001）

10.Bendsøe，M.P.，Sigmund，O.:Material interpolation schemes in topology optimization.Arch.Appl.Mech.69，635-654（1999）

11.Xie，Y.M.，Steven，G.P.:Asimpleevolutionaryprocedureforstructural optimization.Comput.Struct.49，885-896（1993）

12.Xie，Y.M.，Steven，G.P.:Evolutionary Structural Optimization. Springer，Berlin（1997）

13.Rozvany，G.I.N.，Querin，O.M.，Gaspar，Z.，etal.:Weightincreasing effect of topology simplification.Struct.Multidiscip.Optim.25，459-465（2003）

14.Luo，J.，Luo，Z.，Chen，S.，etal.:Anewlevelsetmethodforsystematicdesignofhinge-freecompliantmechanisms.Comput.Methods Appl.Mech.Eng.198，318-331（2008）

15.Wang，M.Y.，Chen，S.，Wang，X.:Design of multimaterial compliant mechanisms using level-set methods.J.Mech.Des.127，941-956（2005）

16.Wang，M.Y.，Wang，X.，Guo，D.:A level set method for structural topology optimization.Comput.Methods Appl.Mech.Eng.192，227-246（2003）

17.Neves，M.M.，Rodrigues，H.，Guedes，J.M.:Generalized topology criterion design of structures with a buckling load criterion.Struct. Optim.10，71-78（1995）

18.Seo，Y.-D.，Youn，S.-K.，Yeon，J.-H.，et al.:Topology optimization of inner-wall stiffener for critical buckling loads of cylindrical containers.In:Multidisciplinary Analysis and Optimization Conference，30 August-1 September.Albany:New York（2004）

19.Neves，M.M.，Sigmund，O.，Bendsøe，M.P.:Topologyoptimization of periodic microstructures with a penalization of highly localized buckling modes.Int.J.Numer.Methods Eng.54，809-834（2002）

20.Neves，M.M.:Analysis and continuum topology optimization of periodic solids with linearized elastic buckling criterion.In: IUTAMSymposiumonTopologicalDesignOptimizationofStructures，MachinesandMaterials:StatusandPerspectives，pp.99-106（2006）

21.Ramm，E.，Kemmler，R.:Stability and Large Deformations in Structural Optimization.Warsaw（2002）

22.Kemmler，R.，Lipka，A.，Ramm，E.:Large deformations and stability in topology optimization.Struct.Multidiscip.Optim.30，459-476（2005）

23.Zhou，M.:Topology optimization for shell structures with linear buckling.Comput.Mech.b0105，795-800（2004）

24.Lund，E.:Buckling topology optimization of laminated multimaterial composite shell structures.Compos.Struct.91，158-167（2009）

25.Lindgaard，E.，Lund，E.:Nonlinear buckling optimization of composite structures.Comput.Methods Appl.Mech.Eng.199，2319-2330（2010）

26.Lindgaard，E.，Lund，E.:A unified approach to nonlinear buckling optimizationofcompositestructures.Comput.Struct.89，357-370（2011）

27.Browne，P.A.，Budd，C.，Gould，N.I.M.，et al.:A fast method for binary programming using first-order derivatives，with application to topology optimization with buckling constraints.Int.J.Numer. Methods Eng.92，1026-1043（2012）

28.Lindgaard，E.，Dahl，J.:On compliance and buckling objective functions in topology optimization of snap-through problems. Struct.Multidiscip.Optim.47，409-421（2013）

29.Sui，Y.K.:ModelingTransformationandOptimizationNewDevelopments of Structural Synthesis Method.Dalian Univer-sity of Technology Press，Dalian（1996）.（in Chinese）

30.Sui，Y.-K.，Ye，H.-L.，Peng，X.-R.:Topological optimization of continuum structure with global stress constraints based on ICM method.In:TheInternationalConferenceonComputationalMethods，December 15-17，2004，Singapore.Computational Methods，pts 1 and 2，pp.1003-1014（2006）

31.Ye，H.-L.，Shen，J.-X.，Sui，Y.-K.:Dynamictologicaloptimaldesign of three-dimensional continuum structures with frequencies constraints.LixueXuebao/Chin.J.Theor.Appl.Mech.44，1037-1044（2012）.（in Chinese）

32.Sui，Y.-K.，Ye，H.-L.:Continuum Topology Optimization Methods ICM.Science Press，Beijing（2013）

33.Sigmund，O.:Morphology-based black and white filters for topology optimization.Struct.Multidiscip.Optim.33，401-424（2007）

34.Sui，Y.-K.，Bian，B.-C.，Ye，H.-L.:Topological optimization of the continuumstructuresubjectedtothebucklingconstraintswithICM method.Chin.J.Comput.Mech.25，345-351（2008）.（in Chinese）

29 June 2015/Revised:4 September 2015/Accepted:7 October 2015/Published online:17 November 2015 ©The Author（s）2015.This article is published with open access at Springerlink.com

✉ Hong-Ling Ye yehongl@bjut.edu.cn

1College of Mechanical Engineering and Applied Electronics Technology，Beijing University of Technology，Beijing 100124，China