MDS矩阵构造方法

李鹏飞，李永强

（1. 中国科学院信息工程研究所信息安全国家重点实验室，北京 100093；2. 中国科学院大学，北京 100049）

MDS矩阵构造方法

李鹏飞1，2，李永强1

（1. 中国科学院信息工程研究所信息安全国家重点实验室，北京 100093；2. 中国科学院大学，北京 100049）

针对MDS矩阵的设计策略做了综述。阐述了MDS矩阵构造中的关键问题，并对当前典型和常见MDS矩阵的构造方法从原理、实现机制等方面进行了分析和讨论。另外，调研了最近几年关于轻量级MDS矩阵的研究成果。关键词：分组密码；最优扩散层；分支数；MDS矩阵；线性变换

本文针对MDS矩阵的设计策略做了综述。归纳总结了常见的构造MDS矩阵的方法，分别为利用线性码构造 MDS矩阵；采用随机检测矩阵的方法来构造 MDS矩阵，通过检测特殊矩阵来构造MDS矩阵，如循环矩阵、Hadamard矩阵、对合矩阵和正交矩阵等，以节省软硬件实现开销；利用一些数学上具有特殊性质的矩阵，如Cauchy矩阵、Vandermonde矩阵构造MDS矩阵；基于简单的移位和异或构造高效的 MDS矩阵；基于线性反馈移位寄存器（LFSR， linear feedback shift register）构造硬件实现友好的迭代型最优扩散层。本文阐述了这些MDS矩阵构造方法中的关键问题，并对当前典型的构造方法从原理、实现机制等方面进行了分析和讨论，另外，随着物联网技术的快速发展，设计和构造轻量级的MDS矩阵受到了越来越多研究人员的关注，本文也对近几年轻量级 MDS矩阵的研究成果进行了调研。

2　基本概念

2.1分支数

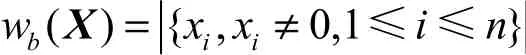
在迭代型密码结构中，将输入差分或者输出掩码非零的S盒称为活跃S盒。一般情况下，如果混淆层是由n个mm×的 S盒并置而成，则扩散层一般设计成的一个置换，其中如图1所示。

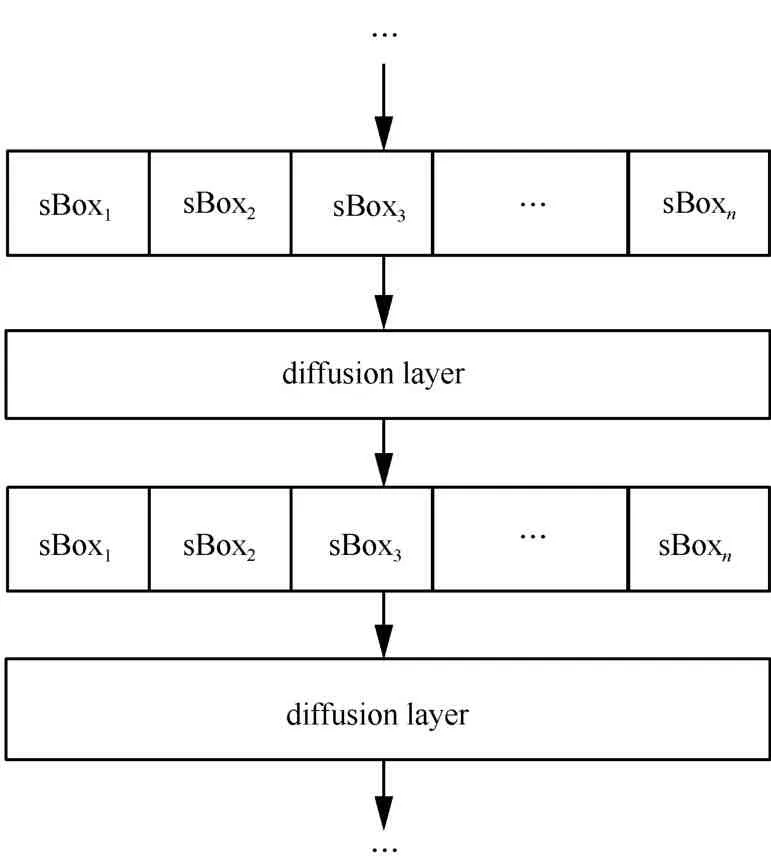
图1　混淆层和扩散层结构

分支数又分为差分分支数和线性分支数，具体定义如下。

定义2扩散层θ的差分分支数定义为［4］

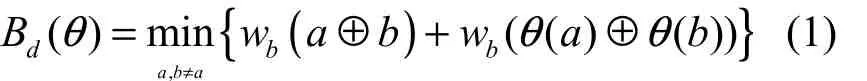
类似于差分分支数，可以给出扩散层线性分支数的定义。

定义3扩散层θ的线性分支数定义为［4］

其中，MT为矩阵M的转置。

差分（线性）分支数即连续两轮的差分（线性）特征中活跃S盒的最小数目，设计者可以根据差分（线性）分支数的大小给出理论上最大差分特征概率（最佳线性逼近偏差）的界，由此可以分析密码算法抵抗差分和线性分析的能力。关于分支数有如下性质［19］。

1）扩散层矩阵M的线性分支数等于转置矩阵MT的差分分支数。2）扩散层的分支数等于其逆变换的分支数。3）扩散层差分分支数达到最大，当且仅当其线性分支数也达到最大。

定义4分支数达到最大的扩散层称为最优扩散层，所对应的矩阵称为MDS矩阵。

2.2线性码

线性码理论对于研究扩散层的分支数很重要，本节结合文献［4，5］，给出线性码的一些重要性质和定理。

定义5域GF（2p）上的线性码C=［n，k，d］是指向量空间GF（2p）n上任意 2个不同向量之间汉明距离至少为d的一个k维子空间，空间的元素称为一个码字。线性码C的最小汉明距离d等于线性码C中非零码字的最小汉明重量。

由定义7可知，若假设线性码C的生成矩阵为G，校验矩阵为H，则有，而且，如果是码C的生成矩阵，则是码C的校验矩阵。

定义8将与线性码C中所有向量都正交的向量集合称为C的对偶码C⊥，具体定义为

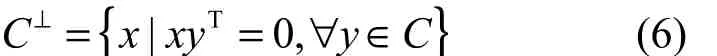
由此可以看出，线性码C的校验矩阵就是C⊥的生成矩阵。

下面介绍几个重要定理。

定理1设C是一个［n，k，d］线性码，H是它的校验矩阵，如果H的任意d−1列线性无关，且存在d列线性相关，则线性码C的最小汉明距离等于d。

定理5 （MDS矩阵的判定定理）设矩阵M是与扩散层θ对应的n阶矩阵，则M为MDS矩阵（即的充要条件是M的任意k阶子式都不为零（1≤k≤n）。

定理6 （MDS矩阵的判定定理）设矩阵M是与扩散层θ对应的n阶矩阵，则M为MDS矩阵（即的充要条件是M的任意k阶子方阵均满秩1≤k≤n）。

2.3构造MDS的相关矩阵

定义 9［20］具有以下形式的n阶方阵A称为循环矩阵。

显然，矩阵A的每一行向量的每一个元素由前一行向量各元素依次循环右移一个位置得到，循环矩阵A可简记为

定义 10［21］一个n阶方阵A称为对合矩阵当且仅当该矩阵满足即，其中，I表示n阶单位阵。

定义 11［21］一个n阶方阵A称为正交矩阵当且仅当该矩阵满足，其中，I表示n阶单位阵，表示矩阵A的转置矩阵。

定义12［9］一个2n×2n矩阵H称为Hadamard矩阵，则它具有如下形式。

定义13［22，23］给定令且则将n阶方阵称为柯西矩阵，其行列式为

定义14［23，24］给定，则满足以下形式的n阶方阵A称为范德蒙（Vandermonde）矩阵。

其行列式为

3　利用线性码构造MDS矩阵

一直以来，MDS码是构造密码算法最优扩散层的主要工具，通过 MDS码构造的扩散层分支数达到最大，具有良好的扩散能力，能够更好地抵抗差分分析、线性分析和其他未知的密码分析。许多分组密码算法如 AES、Khazad、SHARK、Square等扩散层中所使用的 MDS矩阵就是从MDS码中提取出来的。Reed-Solomon码［23，25］是一种 MDS码，它的最小汉明距离达到了最大，可以用来构造MDS矩阵。另外，BCH码［23，26］、Goppa码［27］这2种线性码的最小距离都是可以设计的，通过控制这2种线性码的最小汉明距离，使其达到最大值，即可从它们的生成矩阵提取MDS矩阵。另外，文献［28］提出通过 Gabidulin码来构造MDS码的新方法。

3.1 分支数与线性码的关系

根据线性码的一些重要性质和定理，可利用GF（2）p上的线性码来进一步分析扩散层的分支数，以得到线性码和扩散层分支数间的关系，以下定义参考文献［29］。

由此，将线性码和扩散层联系起来，结合差分分支数的定义 2，可以进一步得到扩散层差分分支数与线性码的关系。

定理 7 扩散层θ的差分分支数等于它的相关线性码中2个不同码字之间的最小汉明距离。这是因为，根据扩散层θ的差分分支数定义2有

得到了扩散层和线性码之间的关系，即可利用线性码来构造MDS矩阵。

3.2 构造MDS矩阵的方法

定理8［5］令C是有限域上的一个［2m， m，m+1］线性码是C的生成矩阵的梯次形，则C定义了如下置换。

4　利用随机检测矩阵来构造MDS矩阵

为了节省软硬件实现的系统资源，减少开销，提高密码算法运行速度，通常根据定理5和定理6通过检测特殊矩阵来构造MDS矩阵，如循环矩阵、Hadamard矩阵、对合矩阵和正交矩阵等。循环矩阵和 Hadamard矩阵可使矩阵中不同元素的数量极其少，对合矩阵可使密码算法加解密一致，节省解密的开销，正交矩阵同样可以使用几乎相同的电路实现加解密操作。

4.1 循环矩阵

由循环矩阵的定义9可知，循环矩阵的元素基本相同，只用实现一行，然后通过不断更新输入向量，便可以得到全部的输出向量，另外，与一般的随机矩阵相比，循环矩阵所对应的扩散层达到最优的概率更大［8］。采用循环矩阵作为扩散层的密码算法很多，典型的是AES算法中列混淆部分所使用的MDS矩阵另外，还有基于分组密码的Hash函数Whirlpool扩散层中使用的MDS矩阵它们均作用在有限域）上。实际中，还可以根据下面2个定理构造循环MDS矩阵。

定理9［31］设为上可逆多项式的系数，c（ x）对应的线性变换其中，D为4阶循环矩阵如果满足以下条件。

其结果两两不等。

则循环矩阵D为MDS矩阵，即线性变换θ（x）分支数达到最大5。

定理10［32］设是上的一个可逆多项式，设其逆多项式为对应的线性变换为其中，D为4阶循环矩阵，如果满足如下条件。

则4阶循环矩阵D为MDS矩阵，线性变换θ（x）分支数达到最大5。

4.2 Hadamard矩阵

由Hadamard矩阵的定义12可知，与循环矩阵类似，Hadamard矩阵的每一行均是第一行的置换，因此节省了软硬件实现开销，采用Hadamard矩阵的典型算法是CLEFIA、Anubis和Khazad。轻量级分组密码算法 CLEFIA中所使用的 2个Hadamard MDS矩阵为H=Had（01，02，04，06）和H=Had（01，08，02，0a），它们均作用在有限域上。Anubis算法中使用的 MDS矩阵和CLEFIA算法中的第一个矩阵相同。Khazad算法中所使用的 MDS矩阵为H=Had（01，03，04，05，06，08，0b，07），它也是作用在有限域上。关于Hadamard矩阵，有如下性质和定理［33，34］。

4.3对合矩阵和正交矩阵

对合矩阵的优点在于可以使用相同的电路实现加解密操作，节省了密码算法加解密的实现开销，典型的是Anubis和Khazad算法扩散层中使用的对合 MDS矩阵。正交矩阵的优点是可以通过实现矩阵的转置来得到逆变换，可以使用几乎相同的电路实现加解密操作，所以，正交矩阵同对合矩阵一样，简化了逆矩阵的实现，使解密实现效率更高。

利用特殊矩阵来构造MDS矩阵的研究成果很多，文献［22］利用MDS码来构造对合MDS矩阵，Sajadieh等［24］提出一种基于有限域GF（2）q构造对合Hadamard MDS矩阵的方法。文献［35］提出了一种构造拥有低汉明重量的对合MDS矩阵。早在2009年，Nakahara等［36］就证明4阶循环MDS矩阵不可能是对合的。ISPEC 2014上，Gupta等［21］又证明了基于有限域的n×n循环对合MDS矩阵是不存在的，同时也证明了基于有限域的2d×2d的循环正交 MDS矩阵也是不存在的。文献［37］从数学角度通过分解循环矩阵，构造出一种新型的循环MDS矩阵。

FSE 2015上，Sim等［38］通过证明一些有关循环矩阵、Hadamard矩阵、Cauchy矩阵和Hadamard-Cauchy矩阵的等价类，提出一个新的算法来搜索具有更少异或数的轻量级对合 MDS矩阵，该算法减少了搜索空间，使MDS矩阵的搜索变得更容易，并且找到了更大维数的 MDS矩阵。FSE 2016上，Liu等［39］通过分析循环矩阵的一些新的等价类性质，缩小了搜索空间，得到了一系列的循环 MDS矩阵，另外，他们提出一种新型的具有类似于循环矩阵性质且具有潜在自逆性的cyclic矩阵，构造出对合left-circulant MDS矩阵。FSE 2016上，Li等［40］直接基于向量空间F2m构造 MDS矩阵，采用非交换元素首次构造了作用在4 bit和8 bit S盒上的4阶和5阶轻量级循环对合 MDS矩阵（这一类型的基于有限域的矩阵之前在文献［21，36］中被证明是不存在的），并且构造了一系列循环非对合 MDS矩阵，循环正交MDS矩阵，Hadamard对合MDS矩阵和Hadamard非对合MDS矩阵，这些轻量级MDS矩阵硬件实现所需的异或数均极少。

由于循环矩阵、Hadamard矩阵、对合矩阵和正交矩阵等特殊矩阵相对于普通矩阵具有更低的软硬件实现代价，所以受到研究人员的青睐，一般来说，利用随机检测矩阵来构造 MDS矩阵，可以找到足够轻量的 MDS矩阵，但由于需要搜索的空间非常大，需要搜索所有可能的置换，所以一般从理论上分析它们的一些等价类特征和自身所具有的一些性质，以此来缩小搜索空间，但当矩阵的维数较大时，直接进行穷举搜索也显得不太现实，此时，一般在具有特定结构的矩阵中搜索MDS矩阵，这样的好处是搜索的空间比较小，可以得到这种特定结构中最轻量的MDS矩阵，但可能会漏失一些更加轻量的其他MDS矩阵。

5　利用数学方法构造MDS矩阵

Cauchy矩阵和Vandermonde矩阵由于具有数学上的特性，通常被用来构造大阶MDS矩阵。

5.1利用Cauchy矩阵构造MDS矩阵

根据Cauchy矩阵的定义13，结合式（9）可知，如果对于任意的i ，j均满足xi各不相同，yi各不相同，且，那么该类型矩阵的任意子方阵均非奇异，由定理5可知，可以很容易地通过Cauchy矩阵来构造MDS矩阵。有不少学者利用Cauchy矩阵来构造MDS矩阵，文献［34］证明了Cauchy-Hadamard型MDS矩阵等效于对合Cauchy-Hadamard型MDS矩阵，并且给出了由 Cauchy-Hadamard型 MDS矩阵构造对合Cauchy-Hadamard型MDS矩阵的方法。文献［41］证明了有限域上 Cauchy矩阵的个数，也证明了Cauchy矩阵一定不是循环移位矩阵。文献［42］提出一种紧凑型的 Cauchy矩阵（CCM， compact cauchy matrices），它们拥有最少的不同元素数目，更加利于软硬件实现，他们还证明所有的紧凑型Cauchy矩阵可以转化为对合紧凑型Cauchy矩阵。文献［43］对 Cauchy矩阵和 MDS矩阵分别从Hadamard矩阵和循环移位矩阵以相互结合的方式构造最优扩散层的方法进行了研究。文献［22］利用Cauchy矩阵的性质构造了新型的对合MDS矩阵。文献［35］提出一种基于Cauchy矩阵构造有效MDS矩阵的一般方法。

5.2利用Vandermonde矩阵构造MDS矩阵

根据Vandermonde矩阵的定义14，结合式（11）可知，当互不相同且不为0时，该类型矩阵的任意子式非零，由定理5可知，可以使用Vandermonde矩阵来构造MDS矩阵。

文献［44］介绍了2个利用Vandermonde矩阵构造 MDS矩阵的方法。文献［24］提出一种使用Vandermonde矩阵构造任意阶对合 MDS矩阵的方法。文献［35］基于Vandermonde和Cauchy矩阵构造了对合Hadamard MDS矩阵。

采用随机检测特殊矩阵来构造MDS矩阵的方法通常只适用于矩阵维数较小时，当需要构造更大维数的 MDS矩阵时，这种方法不适用，此时，可以利用数学上具有某些特性的矩阵来构造MDS矩阵，Cauchy矩阵和Vandermonde矩阵因其独特的结构可用来构造任意阶的MDS矩阵。但由于这类MDS矩阵中元素汉明重量通常较大，实现过程需要消耗很大的软硬件资源，因此，在密码算法设计中不常用。

6　利用移位和异或构造MDS矩阵

基于简单移位和异或构造的扩散层由于具有软硬件实现效率高，能够增强密码算法抵抗时间、能量等密码分析能力的特点，已被很多对称密码算法所使用，比如，我国无线局域网产品中使用的密码算法SM4［45］、3GPP LTE国际加密标准ZUC算法［46］、HIGHT［47］、SHA-256［48］、MD6［49］等，其中，SM4和ZUC中所使用的就是这种类型的最优扩散层，其分支数达到了最大。SM4中的扩散层为中使用了2个最优扩散层，其中一个和SM4中的相同，另外一个是

近几年，有一些利用移位和异或构造 MDS矩阵的研究，文献［50］研究了基于循环移位和异或构造的扩散层分支数达到最优时需要满足的一些必要条件，文献［51］研究了SM4型的扩散层，指出在一定的等价意义下，这样的最优扩散层仅有 2个，文献［52］研究了基于循环移位和异或运算设计的对合线性变换，给出了这类线性变换的计数公式，指出它们的分支数上界为4。

7　利用LFSR构造迭代型最优扩散层

近几年，随着物联网（IoT， Internet of things）技术的发展，射频识别（RFID， radio frequency identification）标签、无线传感器网络（WSN，wireless sensor network）、个人数字助理终端（PDA，personal digital assistant）等微型嵌入式设备越来越发达，由于这些微型嵌入式计算设备在面积、通信能力、电源能量、计算速度和存储空间等方面严峻的资源限制，要保护数据安全和用户隐私就必须设计更加轻量的密码算法，于是，设计更加轻量、安全的部件，特别是扩散层成为研究焦点。

为了满足资源受限设备加解密的需求，节省软硬件实现开销，除了上述利用随机检测矩阵和基于移位和异或构造轻量级 MDS矩阵外，PHOTON轻量级Hash函数族的设计者们［18］还提出一种新的最优扩散层设计策略——迭代型扩散层设计。这种设计方式借用流密码算法中的LFSR的设计思想，如图2所示，每次只更新一个元素，其余元素则通过移位得到。

图2　PHOTON中最优扩散层设计方式

图2中每个 Li选自有限域GF（2n），迭代s步后的最终状态作为扩散层的输出。假设A是LFSR的状态转移矩阵，则这种方式构造的扩散层矩阵是GF（2n）上的n×n矩阵As。此外，轻量级分组密码算法 LED和认证加密算法PRIMATEs［53］的最优扩散层也采用这种方式设计。

状态转移矩阵（也称为相伴矩阵）A的具体形式如下。

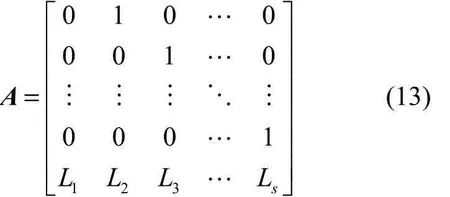
迭代型扩散层的设计在得到MDS矩阵的同时，也具有很高的硬件实现效率，只需实现LFSR且能在不需要增加额外逻辑控制电路的情形下重用已有的存储，因此，十分适合硬件实现，但是，软件需要使用类似于 AES中的查表过程实现该扩散层，矩阵需要用表来存储，消耗一定的存储空间，另外，这种设计方式在节省硬件实现面积的同时，增加了时钟周期，具有一定的延迟，因此，它不适合在延迟性要求比较高的场景下使用。

受到PHOTON扩散层的启发，越来越多的学者把关注点放在了迭代型扩散层的设计上，涌现出了一大批研究成果。FSE 2012上，Sajadieh等［54］对该设计方式进行了扩展，并给出了一系列最优扩散层。他们将图2中线性变换i的选取从有限域GF）扩展到了向量空间上，得到的MDS矩阵可以表示成上的sn×sn矩阵或者GF（2）n上的s×s分块矩阵。由于有限域GF（2）n上的乘法运算是向量空间F2n上的特殊线性变换，因此，Sajadieh等的工作扩展了扩散层的选择空间，这使设计者可能构造出硬件实现代价更低的扩散层。

SAC 2012上，Wu等［55］在Sajadieh等基础上，通过改变线性变换的选择范围，得到了一系列最优分支数为5～9的轻量级扩散层。Augot等［56］摆脱以上方法中复杂的符号计算，构造出了阶数更大的迭代型MDS矩阵。另外，迭代型的MDS矩阵构造还与码理论有关。Berger［57］利用Gabidulin码构造了迭代型MDS矩阵。FSE 2014上，Augot等［26］直接采用BCH码来构造迭代型MDS矩阵。

由于迭代型MDS矩阵具有高延迟的缺点，LFSR需要进行好多拍才能得到输出向量，于是，研究如何构造非迭代型的轻量级 MDS矩阵成为接下来的研究重点。一些学者重新基于有限域来构造轻量级 MDS矩阵，经过精心选择有限域上元素，可以使软硬件实现代价降低。最近，CHES 2014上，Khoo等［58］指出不可约多项式的选取对有限域上元素乘法实现有很大影响，这意味着可以选择有效的不可约多项式来构造 MDS矩阵，节省软硬件实现开销。文献［38］对该性质进行了进一步的研究。

8　MDS矩阵的实现方法

在实际应用中，密码算法需要在不同软硬件平台上高效实现，而扩散层作为密码算法一个很重要的部分，它的实现性能直接影响整个密码算法的高效性能。一般来说，实现 MDS矩阵的常用方法有基于xtime（）乘法［4］、基于字的乘法、查小表、查大表，后2种是通过预置乘法表的方法，利用空间换取时间来提高运行速度。为了节省软硬件资源，提高密码算法运行速度，需要根据不同的应用场景，选用不同的实现方式，在资源空间受限的情况下，适宜采用基于字的乘法实现方式；在资源空间充足的情况下，宜采用查大表的方法实现MDS矩阵［36，59］。

9　结束语

MDS矩阵广泛应用于分组密码算法、Hash函数、认证加密算法，使用 MDS矩阵作为扩散层，可以保证分支数达到最大，从而可以最大限度地保证密码算法在差分和线性分析下的安全性。本文比较系统地阐述了常见的构造 MDS矩阵的方法：从线性码中提取 MDS矩阵；采用随机检测矩阵构造特殊MDS矩阵，如循环MDS矩阵、Hadamard MDS矩阵、对合MDS矩阵和正交MDS矩阵；使用数学上具有特殊性质的矩阵，如Cauchy矩阵和Vandermonde矩阵构造MDS矩阵。本文基于移位和异或构造高效的 MDS矩阵和利用 LFSR构造硬件实现友好的迭代型最优扩散层，介绍了构造 MDS矩阵的原理，并详细给出了各种方法的研究现状以及其中的优缺点，最后，给出了 MDS矩阵的实现方法，设计者可以根据应用场景的不同选用不同的实现方式以提高算法运行速度，节省软硬件资源。

［1］SHANNON C E. Communication theory of secrecy systems［J］. Bell System Technical Journal， 2015， 28（4）：656-715.

［2］BIHAM E， SHAMIR A. Differential cryptanalysis of DES-like cryptosystems［J］. Journal of Cryptology， 1991， 4（1）： 3-72.

［3］MATSUI M. Linear cryptanalysis method for DES cipher［M］// Advances in Cryptology — EUROCRYPT. Berlin Heidelberg：Springer， 1993：386-397.

［4］DAEMEN J， RIJMEN V. The design of rijndael， AES—the advanced encryption standard［M］. Berlin Heidelberg：Springer， 2002.

［5］RIJMEN V， DAEMEN J. The cipher SHARK［C］//Fast Software Encryption. c1996：99-112.

［6］SCHNEIER B， KELSEY J， WHITING D， et al. Twofish： a 128 bit block cipher［C］// The 1st AES Candidate Conference on National Institute for Standards and Technology. c1998.

［7］SCHNEIER B， KELSEY J， WHITING D， et al. The twofish encryption algorithm［M］.1999.

［8］DAEMEN J， KNUDSEN L R， RIJMEN V. The block cipher square［C］//The 4th fast software encryption workshop. c1997：149-165.

［9］BARRETO P， RIJMEN V. The anubis block cipher［EB/OL］. http：//www.larc.usp.br/～pbarreto/AnubisPage.html.

［10］BARRETO P， RIJMEN V. The khazad legacy-level block cipher［J］. Primitive Submitted to NESSIE， 2000.

［11］JUNOD P， VAUDENAY S. FOX： a new family of block ciphers［C］//Selected Areas in Cryptography. c2004：114-119.

［12］SHIRAI T， SHIBUTANI K， AKISHITA T， et al. The 128 bit block cipher CLEFIA［C］//International Workshop on Fast Software Encryption. c2007： 181-195.

［13］GUO J， PEYRIN T， POSCHMANN A， et al. The LED block cipher［C］//International Workshop on Cryptographic Hardware and Embedded Systems. c2011： 326-341.

［14］WATANABE D， FURUYA S， YOSHIDA H， et al. A new keystream generator MUGI［C］//FSE 2002. c2002：179-194.

［15］FILHO G D， BARRETO P， RIJMEN V. The maelstrom-0 Hash function［C］//The 6th Brazilian Symposium on Information and Computer Systems Security. c2006.

［16］GAURAVARAM P， KNUDSEN L R， MATUSIEWICZ K， et al. Grøstl a SHA-3 candidate［EB/OL］. http：//www.groestl.info.

［17］BARRETO P S L M， RIJMEN V. Encyclopedia of cryptography and security［C］//2nd Edn. c2011：1384-1385.

［18］GUO J， PEYRIN T， POSCHMANN A. The PHOTON family of lightweight hash functions［C］// Rogaway-CRYPTO 2011. c2011：222-239.

［19］DAMGÅRD I B. A design principle for hash functions［C］// Advances in Cryptology-CRYPTO'89. c1990： 416-427.

［20］RAO A R， BHIMASANKARAM P.Linear algebra［M］. Hindustan Book Agency.

［21］KISHAN C G， INDRANIL G R. On constructions of circulant MDS matrices for lightweight cryptography［C］// ISPEC. c2014：564-576.

［22］YOUSSEF A M， MISTER S， TAVARES S E. On the design of linear transformations for substitution permutation encryption networks［C］//Workshop On Selected Areas in Cryptography（SAC）. c1997：40-48.

［23］WILLIAMS F J M， SLOANE N J A. The theory of error correcting codes［M］. Elsevier， 1977.

［24］SAJADIEH M， DAKHILALIAN M， MAL H， et al. On construction of involutory MDS matrices from vandermonde matrices in ［C］// Design， Codes Cryptography. c2012：1-22.

［25］LINT J H V. Algebraic geometric codes［M］//Coding theory and design theory. New York ：Springer， 1990： 137-162.

［26］AUGOT D， FINIASZ M. Direct construction of recursive MDS diffusion layers using shortened BCH codes［C］//International Workshop on Fast Software Encryption. c2014： 3-17.

［27］GOPPA V D. A new class of linear correcting codes［J］. Problemy Peredachi Informatsii， 1970， 6（3）： 24-30.

［28］BERGER T P， OURIVSKI A. Construction of new MDS codes from gabidulin codes［C］// ACCT. c2009： 40-47.

［29］杨谱. 分组迭代密码函数的扩散层分析及应用［D］. 西安：西安电子科技大学， 2013. YANG P. Cryptanalysis and applications for diffusion layer of iterated block function［D］. Xi'an： Xidian University， 2013.

［30］JUNOD P， VAUDENAY S. Perfect diffusion primitives for block ciphers［C］//International Workshop on Selected Areas in Cryptography. c2004： 84-99.

［31］何凌云. 分组密码扩散层的改进研究［D］. 杭州： 杭州电子科技大学， 2011. HE L Y. Research on the improvement of block cipher diffusion layer［D］. Hangzhou： Hangzhou Dianzi University， 2011.

［32］郭艳珍， 韩文报， 赵龙， 等. AES列混合变换［J］. 解放军理工大学学报（自然科学版）， 2009 （3）： 232-236. GUO Y Z， HAN W B， ZHAO L， et al. AES mixColumns transfor-mation［J］. Journal of PLA University of Science and Technology（ Natural Science Edition）， 2009（3）： 232-236.

［33］刘丽辉， 徐林杰， 张祖平， 等. 有限域上Hadamard型MDS矩阵研究［J］. 舰船电子工程， 2014（5）：41-45. LIU L H， XU L J， ZHANG Z P， et al. Investigate for MDS matrix of hadamard type on finite fields［J］. Ship Electronic Engineering，2014（5）：41-45.

［34］崔霆， 金晨辉. 对合Cauchy-Hadamard型 MDS矩阵的构造［J］.电子与信息学报， 2010， 32（2）：500-503. CUI T， JIN C H. Construction of involution cauchy-hadamard type MDS matrices［J］. Journal of Electronics & Information Technology，2010， 32（2）： 500-503.

［35］GUPTA K C， RAY I G. On constructions of involutory MDS matrices［C］//International Conference on Cryptology in Africa. c2013：43-60.

［36］NAKAHARA J R， ÉLcio A. A new involutory mds matrix for the AES［J］. Network Security， 2009，9（2）：109-116.

［37］DEHNAVI S M， SHAMSABAD M R M， RISHAKANI A M， et al. Efficient MDS diffusion layers through decomposition of matrices［M］// IACR Cryptology. ePrint Archive， 2015.

［38］SIM S M， KHOO K， OGGIER F， et al. Lightweight MDS Involution Matrices［C］//FSE 2015. c2015.

［39］LIU M， SIM S M. Lightweight MDS generalized circulant matrices［C］//Fast Software Encryption. c2016.

［40］LI Y， WANG M. On the construction of lightweight circulant involutory MDS matrices［C］//Fast Software Encryption. c2016.

［41］崔霆， 金晨辉. 分组密码 Cauchy 型 MDS 扩散结构的几点注记［J］. 电子学报， 2011， 39（7）： 1603-1607. CUI T， JIN C H. Several remarks of Cauchy type MDS diffusion layer for block cipher［J］. Acta Electronica Sinica， 2011， 39（7）：1603-1607.

［42］CUI T， JIN C， KONG Z. On compact cauchy matrices for substitution-permutation networks［J］. IEEE Transactions on Computers，2015， 64（7）： 2098-2102.

［43］马庆禄， 魏悦川， 潘晓中. 基于 Cauchy 矩阵的线性变换的研究［J］. 计算机应用研究， 2015， 32（7）： 2144-2146. MA Q L， WEI Y C， PAN X Z. Research on linear transformations based on Cauchy matrix［J］. Application Research of Computers，2015， 32（7）， 2144-2146.

［44］LACAN J， FIMES J. Systematic MDS erasure codes based on vandermonde matrices［J］. IEEE Communications Letters， 2004，8（9）： 570-572.

［45］无线局域网产品中使用的SMS4算法［EB/OL］. http：//www.oscca. gov.cn/UpFile/200621016423197990.pdf. SMS4 algorithm used in wireless LAN products［EB/OL］. http：//www.oscca.gov.cn/UpFile/200621016423197990.pdf.

［46］ETSI/SAGE TS 35.222-2011， specification of the 3GPP confidentiality and integrity algorithms 128-EEA3 & 128-EIA3； document 2：ZUC Specification［S］.

［47］HONG D， SUNG J， HONG S， et al. HIGHT： a new block cipher suitable for low-resource device［M］//Cryptographic Hardware and Embedded Systems-CHES 2006. Berlin Heidelberg： Springer， 2006：46-59.

［48］National institute of standards and technology［S］. The Secure Hash Standard， 2002.

［49］RIVEST R L， AGRE B， BAILEY D V， et al. The MD6 hash function［J］. Invited Talk at CRYPTO， 2008.

［50］ZHANG W， WU W， FENG D， et al. Some new observations on the SMS4 block cipher in the Chinese WAPI standard［M］//Information Security Practice and Experience. Berlin Heidelberg： Springer，2009： 324-335.

［51］王金波. 基于循环移位构造最优线性变换［C］. 中国密码学会2007年会，成都. c2007：306-307. WANG J B. The optimal permutation in cryptography based on cyclic-shift linear transform［C］//China Crypt'2007，Chengdu. c2007： 306-307.

［52］李瑞林， 熊海， 李超. 基于循环移位和异或运算的对合线性变换研究［J］. 国防科技大学学报， 2012， 34（2）： 46-50. LI R， XIONG H， LI C. Research on involutional linear transformations based on rotation and XOR［J］. Journal of National University of Defense Technology， 2012， 34（2）： 46-50.

［53］ANDREEVA E， BILGIN B， BOGDANOV A， et al. PRIMATEs v1.02 submission to the CAESAR competition［EB/OL］. http：// competitions.cr.yp.to/round2/primatesv102.pdf.

［54］SAJADIEH M， DAKHILALIAN M， MALA H， et al. Recursive diffusion layers for block ciphers and Hash functions［C］// FSE 2012. c2012：385-401.

［55］WU S， WANG M， WU W.Recursive diffusion layers for （lightweight）block ciphers and Hash functions［C］//SAC 2012. c2012： 355-371.

［56］AUGOT D， FINIASZ M. Exhaustive search for small dimension recursive MDS diffusion layers for block ciphers and hash functions［C］// 2013 IEEE International Symposium on Information Theory （ISIT）. c2013：1551-1555.

［57］BERGER T P. Construction of recursive MDS diffusion layers from gabidulin codes［C］//Indocrypt. c2013：274-285.

［58］KHOO K， PEYRIN T， POSCHMANN A， et al. FOAM： searching for hardware optimal spn structures and components with a fair comparison［C］//Cryptographic Hardware and Embedded Systems （CHES）. c2014： 433-450.

［59］刘鸿博， 金晓刚， 段俊红. 分组密码中 MDS矩阵的实现方法效能分析［J］. 信息安全与通信保密，2013（10）：77-78. LIU H B， JIN X G， DUAN J H. Efficiency analysis of MDS matrix applied in block cipher［J］. Information Security and Communications Privacy， 2013（10）：77-78.

Construction of MDS matrices

LI Peng-fei1，2， LI Yong-qiang1

（1. The State Key Lab of Information Security， Institute of Information Engineering， Chinese Academy of Sciences， Beijing 100093， China；2. University of Chinese Academy of Sciences， Beijing 100049， China）

A survey for MDS matrices design strategy was made. Design strategies and the key issues during the design were elaborated， and many aspects such as principle and implementation mechanisms of some typical and common construction of MDS matrices were analyzed and discussed. In addition， the research results on lightweight MDS matrices in recent years were investigated.

block cipher， optimal diffusion layer， branch number， MDS matrix， linear transformation

1　引言

随着信息技术的快速发展，互联网已经融入人们生活的方方面面，然而，人们在享受互联网带来便利的同时，信息安全问题也越来越突出。现代密码学作为信息安全的核心和关键技术，在保护数据安全和用户隐私上发挥着巨大的作用。分组密码因其加、解密速度快，便于软硬件实现和易于标准化等特点，受到广泛关注且成为密码学研究的热点课题。分组密码在对大批量数据加密的应用中扮演着举足轻重的作用，它们以硬件、软件等不同的实现方式广泛应用在个人通信、电子支付、数据库加密等诸多领域。早在1949年，香农（Shannon）在他的《保密系统的通信理论》中就提到密码系统设计的2种基本方法：混淆和扩散［1］，这是现今密码算法设计和分析的基础。现在广泛使用的分组密码算法通常采用迭代型结构，迭代型是指所有轮（除第一轮和最后一轮外）均采用相同轮变换。迭代型分组密码设计中最重要的2个基本部件是混淆层（confusion layer）和扩散层（diffusion layer）。混淆层通常使用非线性的几个并置S盒来构造，扩散层由线性的变换函数构成。扩散层作为迭代型分组密码的一个很重要的部件，它的设计不但影响分组密码算法的安全性，而且影响分组密码在软硬件中的实现效率。性能良好的扩散层可以有效地抵抗一些著名的密码攻击，如差分密码分析［2］和线性密码分析［3］。扩散层的安全性能主要由Daemen提出来的分支数［4］概念来衡量，扩散层的分支数越小，分组密码越容易遭受差分分析、线性分析以及一些未知分析方法的攻击；反之，分支数越大，扩散层的扩散效果越好，安全性越好。在实际设计中，最受瞩目的是那些分支数达到最大时的扩散层，简称最优扩散层，所对应的矩阵称为 MDS（maximum distance separable）矩阵。MDS矩阵首次被使用在分组密码SHARK［5］的设计中，随后，越来越多的分组密码算法将 MDS矩阵用于扩散层的设计中，如Rijndael［4］、Twofish［6，7］、Square［8］、Anubis［9］、Khazad［10］、FOX［11］、CLEFIA［12］、LED［13］等。流密码算法也使用 MDS矩阵作为扩散层，如MUGI［14］。另外，散列函数，如 Maelstrom［15］、Grøstl［16］、Whirlpool［17］和PHOTON轻量级散列函数族［18］等都将MDS矩阵作为扩散层使用。

The National Natural Science Foundation of China （No.61379142， No.61303255）

TP393

A

10.11959/j.issn.2096-109x.2016.00063

2016-04-27；

2016-05-30。通信作者：李鹏飞，lipengfei@iie.ac.cn

国家自然科学基金资助项目（No.61379142， No.61303255）

李鹏飞（1991-），男，陕西渭南人，中国科学院信息工程研究所硕士生，主要研究方向为密码学。

李永强（1982-），男，吉林集安人，博士，中国科学院信息工程研究所副研究员，主要研究方向为对称密码算法关键部件的构造、对称密码算法分析。