有效的基于混沌映射的三方认证密钥协商协议

李雄，吴凡，廖俊国，刘玉珍

（1. 湖南科技大学计算机科学与工程学院，湖南 湘潭411201；2. 厦门工学院计算机科学与工程系，福建 厦门361021）

有效的基于混沌映射的三方认证密钥协商协议

李雄1，吴凡2，廖俊国1，刘玉珍1

（1. 湖南科技大学计算机科学与工程学院，湖南 湘潭411201；2. 厦门工学院计算机科学与工程系，福建 厦门361021）

由于良好的密码特性，混沌映射被用于设计密钥协商协议。在多数基于混沌映射的口令三方密钥协商协议中，服务器需存储用户口令表，使这些协议容易遭受口令相关的攻击，且一旦口令表泄露，将带来巨大的安全隐患。针对这些安全问题，提出了一个新的基于混沌映射口令三方认证密钥协商协议，服务器无需维护用户口令表，避免了口令相关的攻击。同其他相关协议相比，所提协议在增强安全性的同时，大大提高了协议的执行效率。

混沌映射；密钥协商；认证；口令

1　引言

随着计算机网络的快速发展和广泛应用，其安全问题日益凸显，如何保护网络会话的安全性变得尤为重要。密钥协商协议可以使2个或多个实体通过公开信道建立共享的会话密钥，能有效解决对称密码方案在应用中的密钥分发问题，是信息安全领域的重要基础研究问题。在早期的密钥协商协议［1，2］中，服务器和用户通过共享长期口令进行密钥协商。因此，攻击者可能从服务器处窃取口令表或通过字典攻击获取用户的口令。在最近的密钥协商协议设计中，研究者们极力避免此类问题，并提出了多个两方（服务器—用户）口令密钥协商协议［3～8］。在这些方案中，用户可以自由选择所持有的口令。而且，为了增强安全性和提供更好的服务，其中一些协议［3，5，7，8］提供了用户自由选择和更换口令以及保护用户匿名等特性。

上述两方口令密钥协商协议非常适用于“客户—服务器”结构，而不太适用于“客户—客户”结构。在大规模点对点网络环境中，用户所需持有的口令数量与通信实体的数量成比例增加。为克服该问题，多个三方口令密钥协商协议［9～20］被提出，在这类协议中，通信双方在可信或半可信第三方的协助下生成共享的会话密钥。

混沌系统具有伪随机性、遍历特性，且输出对初始条件非常敏感，当前轨迹的微小变化和扰动就会导致后续状态的显著不同。混沌系统的这些特性正好满足设计密码系统所需的混淆和扩散原则，并被人们广泛应用于设计密码系统，如对称密码算法、散列函数等。最近，研究者们将混沌系统引入密钥协商协议研究中，设计了多个基于切比雪夫混沌映射（chebyshev chaotic map）的三方密钥协商协议［9～11，14，16，18，19］。2010年，Wang等［14］基于混沌映射提出一个三方密钥协商协议，但该协议被Yoon等［18］指出是不安全的。2013年，Lee等［10］和Xie等［16］分别提出基于混沌映射的密钥协商协议。在上述协议中，用户需要与服务器共享长期私钥以完成相互认证和密钥协商。特别在文献［14，16，18］中，用户的身份通过明文方式传输，增加了模仿攻击的风险。2012年，Lai等［9］基于混沌映射提出一个新的三方密钥协商协议，在该方案中，用户可以自由选择所持有的口令并能保护用户的匿名性。但Zhao等［19］指出Lai等协议［9］不能抵抗内部攻击和离线口令猜测攻击，在此基础上他们提出一个新的方案并声称是安全的。经过分析，本文发现Zhao等［19］的协议不能真正达成用户和服务器的相互认证。此外，在该方案中，服务器使用2个密钥，在增加不安全因素的同时降低了协议效率。在上述基于混沌映射的口令三方密钥协商协议中，服务器需存储用户口令表，使这些协议容易遭受内部攻击等口令相关的攻击，且一旦口令表泄露，将带来巨大的安全隐患。针对这些安全问题，本文提出一个新的基于混沌映射口令三方认证密钥协商协议，服务器无需维护口令表进行密钥协商。通过分析和比较，本文协议在增强安全性的同时，提高了协议执行效率。

2　预备知识

2.1切比雪夫混沌映射及困难问题

定义1切比雪夫多项式。

设n是一个整数，x是区间［-1， 1］的一个变量。切比雪夫多项式 Tn（x）：［-1， 1］→［-1， 1］定义为Tn（x）= cos（narccos（x））。

根据定义 1，切比雪夫多项式满足迭代关系Tn（x）=2xTn-1（x）-Tn-2（x），n≥2，其中，T0（x）= 1，T1（x）= x。

定义2切比雪夫多项式的混沌特性。

当n＞1时，n维切比雪夫多项式映射Tn（x）：［-1， 1］→［-1， 1］是一个具有不变测度为的混沌映射。

定义3切比雪夫多项式的半群特性。

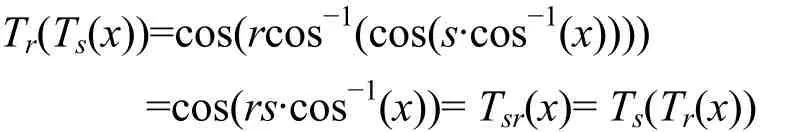
其中，r和s是2个正整数，x∈［-1， 1］。

2008年，Zhang［21］进一步扩展了定义3，证明了定义在区间（-∞， +∞）上的切比雪夫多项式仍具有半群特性，即对Tn（x）= （2xTn-1（x）-Tn-2（x））mod p，这里n ≥ 2，x∈（-∞， +∞），p是一个大素数，有Tr（Ts（x））=Trs（x）=Tsr（x）=Ts（Tr（x））mod p。

定义4离散对数问题（DLP， the discrete logarithm problem）。

给定2个元素x和y，找到一个整数r，使Tr（x）=y。

定义5Diffie-Hellman问题（DHP， the diffie-hellman problem）。

给定3个元素x、Tr（x）和Ts（x），计算Trs（x）。

现在一般认为这2个问题是难解的，即不存在多项式时间算法以不可忽略的概率解决上述 2个问题，这也为基于这2个难题设计安全协议提供了可能性。

2.2安全假设

假设1敌手能窃听、拦截或篡改公开信道中所有的通信消息，且当用户的智能卡丢失时，敌手能通过能量分析等方法［22，23］获取用户智能卡中存储的数据。

假设2服务器S的主密钥x、散列函数及对称加解密算法是安全的，即敌手没有多项式时间算法解决这些问题。

假设3用户的身份标识和口令分别取自 2个不同的有限集合，敌手能在多项式时间内猜测其中之一。但根据文献［24， 25］，敌手在多项式时间内同时猜测出身份标识及对应的口令是困难的。

3　新的基于混沌映射的三方密钥协商协议

本节将提出一个新的基于混沌映射的三方口令密钥协商协议。本协议包含3个阶段：初始化阶段、认证与密钥协商阶段以及口令变更阶段。表1给出了本文使用到的符号及其说明。

表1　符号及说明

3.1初始化阶段

S选择一个随机数s∈（-∞， +∞）、一个系统主密钥x和一个大素数p。当用户希望加入系统时，需要向服务器S注册。注册过程以用户A为例说明，具体如下。

1）A⇒S：（IDA， HPWA）

用户A自由选择身份标识IDA和口令PWA，并产生一个随机数bA。A计算HPWA= h（PWA||bA），并将注册请求（IDA， HPWA）通过安全信道发送给服务器S。

2）S⇒A：智能卡

当收到用户A的注册请求消息（IDA，HPWA），S产生一个随机数 aA，计算 DA1=h（IDA||aA）⊕h（x）⊕HPWA和DA2=h（IDA||aA）⊕h（x||aA），并将DA1、DA2、aA和s 存储在智能卡中。最后，S将智能卡通过安全方式发送给用户A，如通过面对面的方式。

3）A⇒智能卡：（DA3， DA4）

A计算 DA3=h（IDA||PWA||bA）和 DA4=h（IDA⊕PWA）⊕bA，并将DA3和DA4存储在智能卡中。

3.2认证与密钥协商阶段

当用户A和B需要进行安全通信时，可以在服务器的协助下进行相互认证并协商一个共享的密钥。本阶段执行步骤如下，流程如图 1所示。

1）A→B：m1

A将智能卡插入终端，输入身份标识IDA和口令 PWA，智能卡计算 bA'=DA4⊕h（IDA⊕PWA）并检查如果不相等，智能卡终止会话；否则，智能卡产生一个随机数rA，计算

HPWA= h（PWA||bA'），

CA1= DA1⊕HPWA⊕rA，

CA2= DA2⊕rA，

CA3= TrA（s），

CA4= h（CA1||CA2||CA3||aA）。

A将会话请求m1= ｛CA1， CA3， CA4， aA｝发送给B。

2）B→S：（m1， m2）

跟A相似，B插入智能卡，输入身份标识IDB和口令PWB，智能卡计算bB'=DB4⊕h（IDB⊕PWB）并检查。如果它们不相等，智能卡终止会话；否则，B产生一个随机数rB，计算

HPWB= h（PWB||bB'），

CB1= DB1⊕HPWB⊕rB，

CB2= DB2⊕rB，

CB3= TrB（s），

CB4= h（CB1||CB2||CB3||aB）。

最后，B将（m1， m2= ｛CB1， CB3， CB4， aB｝）发送给服务器S。

图1　认证与密钥协商阶段流程

3）S→B：（m3， m4）

当收到消息（m1， m2），S计算CA2'=h（x||aA）⊕CA1⊕h（x）和CB2' =h（x||aB）⊕CB1⊕h（x）。然后，检查和如果两者中任意一个不成立，服务器S拒绝会话。否则，S产生2个随机数aA'和aB'，计算

CA5= h（x||aA）⊕h（x||aA'），

CA6= aA'⊕h（x||aA'），

CA7= h（CA2'||CA5||CA6||aA'），

CB5= h（x||aB）⊕h（x||aB'），

CB6= aB'⊕h（x||aB'），

CB7= h（CB2'||CB5||CB6||aB'）。

S将认证消息m3= ｛CA5， CA6， CA7｝和m4= ｛CB5， CB6， CB7｝发送给B。

4）B→A：（m3， CB3， CB9）

当收到S发送的消息（m3， m4）后，B计算CB8= DB2⊕h（IDB||aB）和 aB''=CB8⊕CB6⊕CB5，并检查如果它们不相等，B终止会话。否则，B计算

skBA= TrB（CA3），

CB9= h（CA3||CB3||skBA），

DB1' =CB1⊕h（IDB||aB）⊕h（IDB||aB''），

DB2' =CB8⊕CB5⊕h（IDB||aB''）。

B将 DB1，DB2和 aB分别替换为 DB1'，DB2' 和aB''，将skBA作为与A共享的会话密钥。最后，B将消息（m3， CB3， CB9）发送给A。

5）当收到B发送的消息（m3， CB3， CB9），A计算CA8=DA2⊕h（IDA||aA），aA'' =CA8⊕CA6⊕CA5，并检查如果等式不成立，A终止会话；否则，A计算skAB= TrA（CB3），CA9= h（CA3||CB3||skAB），并检查如果等式不成立，A终止会话；否则A计算DA1' =CA1⊕h（IDA||aA）⊕ h（IDA||aA''）， DA2'=CA8⊕ CA5⊕h（IDA||aA''）。最后，A将DA1，DA2和aA分别替换为DA1'，DA2'和aA''，skAB作为与B共享的会话密钥保障后续的安全通信。

3.3口令变更阶段

当用户需要变更口令时，A将智能卡插入读卡器，输入身份标识 IDA口令 PWA。智能卡计算bA'=DA4⊕h（IDA⊕PWA），检查 DA3？=h（IDA|| PWA||bA'）。如果不相等，智能卡拒绝请求；否则，A输入一个新的口令PWAnew，智能卡产生一个新的随机数bAnew，计算

HPWA= h（PWA||bA'），

HPWAnew= h（PWAnew||bAnew），

DA1new= DA1⊕HPWAnew⊕HPWA，

DA3new= h（IDA||PWAnew||bAnew），

DA4new= h（IDA⊕PWAnew）⊕bAnew。

最后，A将 DA1，DA3和 DA4分别替换为DA1new、DA3new和DA4new。

4　安全性分析

本节分析本文所提方案的安全性，安全性分析表明，本文方案能够抵抗多种常见的攻击。

4.1内部攻击

在身份认证方案和基于口令的密钥协商协议中，由于在注册或初始化阶段用户将身份标识和口令以明文方式发送给服务器，一旦服务器内部人员获得用户的身份标识和口令，这类方案容易遭受内部攻击。在本文方案的初始化阶段，用户A发送（IDA，HPWA）给服务器S请求注册，这里IDA是用户 A 选择的身份标识，HPWA= h（PWA||bA），PWA是用户选择的口令，bA是用户选择的随机数。这里可以看出，用户的真实口令通过随机数bA被散列函数所保护，特权内部攻击者无法获得用户的真实口令，因此，本文方案可以抵抗内部攻击。而在其他相关协议［10，11，16］的注册阶段，用户直接通过与服务器共享明文口令或直接传输共享的密钥va，使这些方案容易遭受内部攻击。

4.2离线口令猜测攻击

以A为例分析离线口令猜测攻击。根据第2.2节的安全性假设，攻击者可以从公开信道获取与A相关的消息｛CA1，CA3，CA4，aA｝和｛CA5，CA6，CA7｝。此外，还假设攻击者获得用户 A的智能卡并通过能量分析等方法［22，23］获得了智能卡中的数据｛DA1，DA2，DA3，DA4，aA，s｝。根据假设3，攻击者无法同时猜测出用户的身份标识和口令信息，所以攻击者无法从 DA3和 DA4获得IDA、PWA和bA。当攻击者从CA1、CA3、DA1、CA5、CA6、CA7猜测口令时，攻击者必须获得S的主密钥x。所以，本文协议能够抵抗离线口令猜测攻击。

4.3模仿攻击

若攻击者希望模仿用户A，则其必须能够计算有效的会话请求消息m1= ｛CA1，CA3，CA4，aA｝。但从第4.2节的分析可知，攻击者无法获得用户的身份标识IDA、口令PWA和随机数bA，所以在未知IDA、PWA和bA的情况下，攻击者无法计算正确的消息CA1和CA4。

同理，在未知IDB、PWB和bB的情况下，攻击者无法伪造用户B的会话请求消息m2= ｛CB1，CB3，CB4，aB｝。此外，为了模仿用户B产生响应信息 CB9，攻击者必须能计算 skBA=TrB（CA3），进而攻击者需要从CB3获得随机数rB，而这将面临基于混沌映射的离散对数问题。

综上，攻击者无法有效进行模仿攻击。

4.4服务器伪装攻击

为了有效模仿服务器 S，攻击者必须分别为A和B计算有效的消息m3= ｛CA5，CA6，CA7｝和m4= ｛CB5，CB6，CB7｝。但在未知S主密钥x的情况下，攻击者无法计算h（x||aA），h（x||aA'），h（x||aB）和h（x||aB'）。所以，本文协议能够避免服务器伪装攻击。

4.5重放攻击

重放攻击是身份认证和口令密钥协商协议中一种常见的安全威胁，在这种攻击中，攻击者通过重放用户以前发送过的消息达到身份认证和密钥协商的目的。在本文方案的每次会话中，用户A和B分别产生随机数rA和rB以保证会话的新鲜性。当攻击者重放用户A和B以前发送过的消息m1和m2时，为了最终生成会话密钥，攻击者必须计算出随机数rA或rB，而这将面临解基于混沌映射的 Diffie-Hellman问题。因此，随机数机制使每次会话的消息与其他会话的消息都不相同，而一次会话的随机数只对当次会话有效，有效地避免了重放攻击。

4.6用户匿名

用户匿名在电子商务、移动计算等领域具有重要应用，可以保护用户的购物习惯及用户的移动轨迹等信息。在本文方案中，用户A和用户B的真实身份标识IDA和IDB没有包含在公开信道上传输的通信消息中。如对用户 A来说，数据CA1= h（IDA||aA）⊕h（x）⊕rA包含用户的身份标识IDA和随机数rA。但由于无法获得x和rA，攻击者无法获得用户A的真实身份标识IDA。因此，本文协议能保护用户匿名。

4.7相互认证

4.8自由选择和变更口令

在基于口令的身份认证和密钥协商协议中，用户自由选择和变更口令增强了用户的友好性和易用性，是一种理想的功能特性。在文献［10， 12］等协议中，用户必须与服务器S共享长期私钥进行密钥协商；而在文献［9］的协议中，由于用户的个人信息经过服务器的密钥加密后存储在智能卡中，无法实现自由变更口令。本文协议允许用户自由选择方便自己记忆和使用的口令来进行密钥协商，在降低安全风险的同时增强了用户易用性。此外，本文协议允许用户在客户端直接变更口令，而无需远程服务器的协助，在增强用户易用性的同时减轻了通信代价。

4.9前向安全

前向安全是指即使系统主密钥和用户的口令或长期私钥被攻击者获得，攻击者也无法获得用户密钥泄露之前的协商得到的会话密钥。在本文协议中，假设攻击者获得了S的主密钥x以及用户A和B的口令，攻击者可以从公开信道的通信消息中获得TrA（s）和TrB（s），显然攻击者无法计算用户A和用户B的会话密钥skAB= TrA（TrB（s））= TrArB（s）=TrB（TrA（s））= skBA，因为要获得rA或rB，攻击者将面临解基于混沌映射的离散对数问题，而直接从TrA（s）和TrB（s）计算TrArB（s）将面临解基于混沌映射的 Diffie-Hellman问题。因此，本文协议能确保会话密钥的前向安全性。

4.10已知密钥安全

已知密钥安全是指即使攻击者获得当前会话以前的会话密钥，也不影响当前会话的安全。在本文方案中，在每次成功的会话后，用户A和用户B共享一个会话密钥TrArB（s），这里的rA和rB是此次会话中分别由用户A和用户B产生的随机数。由于每一次会话用户A和用户B都产生新的随机数rA和rB，且rA和rB只对当次会话有效，所以，获得当前会话之前的会话密钥无助于攻击者获得当前会话的会话密钥。因此，本文协议能确保已知密钥安全。

5　同相关方案的比较

本节从安全性和效率出发，给出了本文方案同其他相关基于混沌映射的三方密钥协商协议［9～11，16，19］的比较。

安全性比较如表2所示，√表示具有某种安全特性，×表示不具有某种安全特性，N/A 表示未提及或不适用。从表2可以看出，其他相关方案或多或少存在一定的安全缺陷，而本文方案则能抵抗大部分已知攻击。

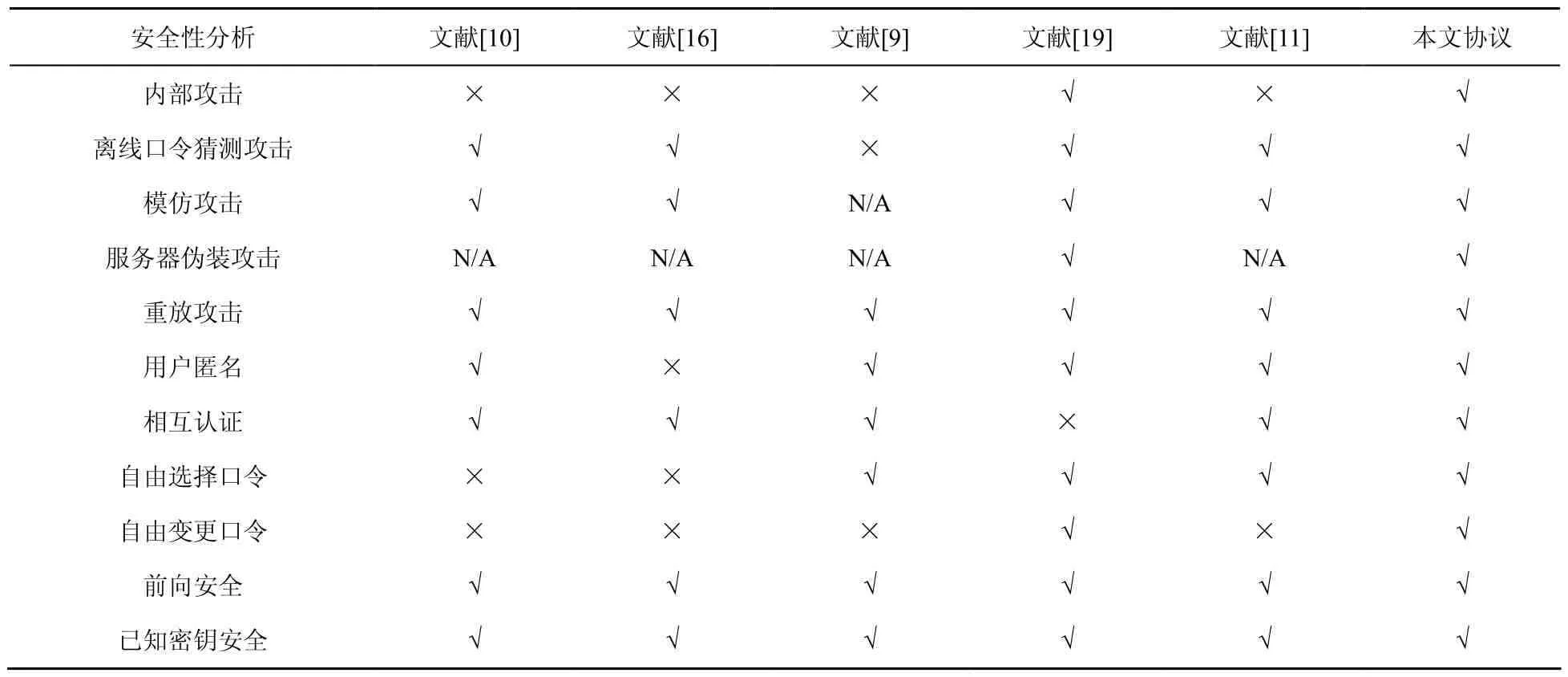
表2　安全性比较

接下来进行效率比较，为计算各种安全算法的时间消耗量，给出如下说明。

1）本文使用 MIRACL C/C++函数库完成各种安全算法的实验分析，采用配置为 CPU Intel（R）Core 2 T6570，2.1 GHz，4 G内存，32 bit Windows7 操作系统的笔记本进行实验，实验程序由Visual C++ 2008编写。

2）为获得切比雪夫混沌多项式的实验结果，本文使用文献［26］中的方法，该方法采用从左至右的方法处理n阶切比雪夫多项式的每一比特数据，n为1 024 bit。等式Tn（s）= 2sTn-1（s）-Tn-2（s）mod p可以由如下矩阵表示。

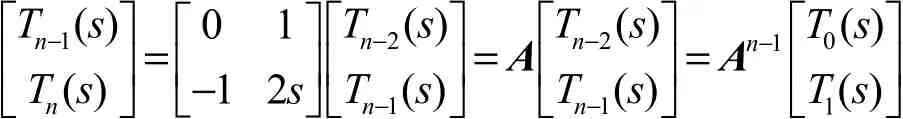
3）使用 AES模拟对称加密/解密算法的运算量。

4）使用SHA-1模拟散列函数的运算量。

各种密码算法执行一次运算的时间消耗量如表3所示。

表3　密码算法时间消耗

本文方案同其他相关方案的性能比较如表 4所示。表4列出了每个方案4个方面的运算量，即用户A、用户B、服务器S的时间消耗量和总的时间消耗量。在本文协议中，用户A、用户B、服务器 S及总的运算量分别为 2TC+8TH、2TC+8TH、8TH和 4TC+24TH，而文献［9，10，16，19］中的协议，用户和服务器需要分别执行3次和 2次切比雪夫多项式运算。文献［11］的协议中，用户和服务器分别需要执行 2次切比雪夫多项式运算。从表4可以明显看出，本文协议执行一次协议总的时间消耗量为562.999 2 ms，具有最高的执行效率。特别在服务器端，本文方案所需运算量最小，显然这有利于大规模并发网络中的数据处理。此外，同其他相关方案相比，由于本文方案具有更高的安全特性，因此，本文方案更适用于现实应用中。

6　结束语

针对最近提出的基于混沌映射的三方密钥协商协议存在的安全性问题，本文提出了一个有效

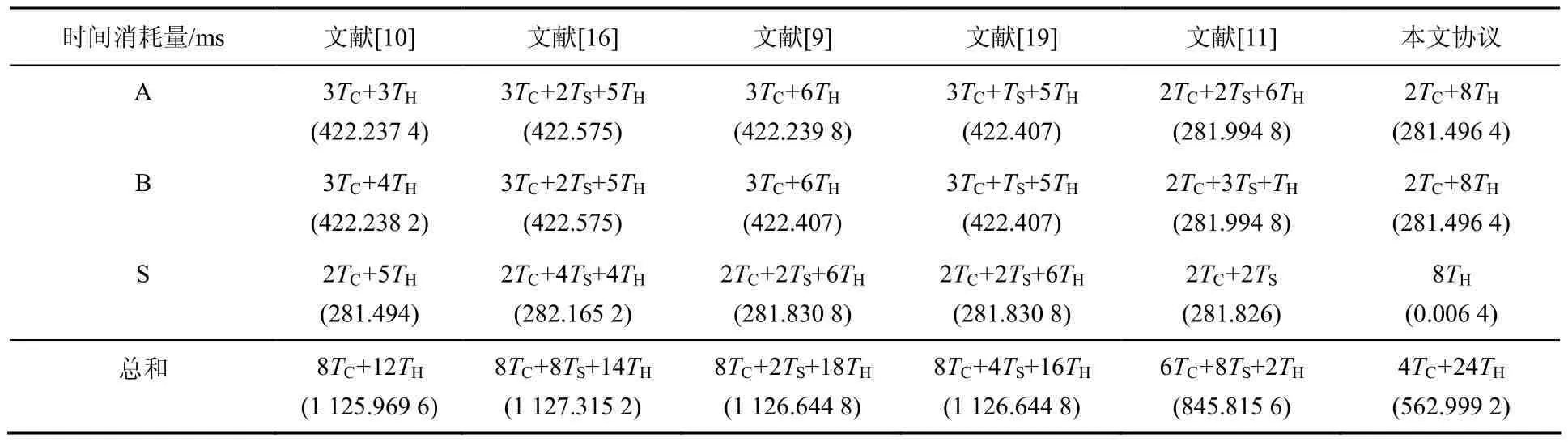
表4　性能比较

的基于混沌映射的三方口令密钥协商协议。同其他相关协议相比，本文协议具有用户匿名、用户自由选择和变更口令等用户友好特性，同时本文方案弥补了相关协议的安全性缺陷，具有更高的安全性。此外，同其他协议相比，本文协议具有更高的计算效率。因此，本文协议更加适用于大规模网络环境下的安全通信。

［1］KATZ J， OSTROVSKY R， YUNG M. Efficient password-authenticated key exchange using human-memorable passwords［J］. Lecture Notes in Computer Science， 2001（4）：475-494.

［2］RAIMONDO M D， GENNARO R. Provably secure threshold password-authenticated key exchange［J］. Journal of Computer and System Sciences， 2006， 72（9）： 507-523.

［3］GUO C， CHANG C C. Chaotic maps-based password-authenticated key agreement using smart cards［J］. Communications in Nonlinear Science and Numerical Simulation， 2013， 18（6）： 1433-1440.

［4］LEE C C， CHEN C L， WU C Y， et al. An extended chaotic maps-based key agreement protocol with user anonymity［J］. Nonlinear Dynamics， 2012， 69（1/2）： 79-87.

［5］LI C T， LEE C C， WENG C Y. An extended chaotic maps based user authentication and privacy preserving scheme against DoS attacks in pervasive and ubiquitous computing environments［J］. Nonlinear Dynamics， 2013， 74（4）：1133-1143.

［6］LI X， ZHANG Y. A simple and robust anonymous two-factor authenticated key exchange protocol［J］. Security and Communication Networks， 2013， 6（6）： 711-722.

［7］TAN Z. A chaotic maps-based authenticated key agreement protocol with strong anonymity［J］. Nonlinear Dynamics， 2013，72（1/2）：311-320.

［8］WU F， XU L L. Security analysis and improvement of a privacy authentication scheme for telecare medical information systems［J］. Journal of Medical Systems， 2012， 37（4）： 1-9.

［9］LAI H， XIAO J， LI L， et al. Applying semigroup property of enhanced chebyshev polynomials to anonymous authentication protocol［J］. Mathematical Problems in Engineering， 2012（6）： 589-597. ［10］LEE C C， LI C T， HSU C W. A three-party password-based authenticated key exchange protocol with user anonymity using extended chaotic maps［J］. Nonlinear Dynamics， 2013， 73（1/2）：125-132.

［11］LIN H Y. Chaotic map-based three-party authenticated key agreement［J］. Security and Communication Networks， 2014， 7（12）：2469-2474.

［12］LV C， MA M， LI H， et al. An novel three-party authenticated key exchange protocol using one-time key［J］. Journal of Network and Computer Applications， 2013， 36（1）： 498-503.

［13］TSAI H C， CHANG C C. Provably secure three party encrypted key exchange scheme with explicit authentication［J］. Information Sciences， 2013， 238（7）：242-249.

［14］WANG X， ZHAO J. An improved key agreement protocol based on chaos［J］. Communications in Nonlinear Science and Numerical Simulation， 2010， 15（12）： 4052-4057.

［15］WU S， CHEN K， PU Q， et al. Cryptanalysis and enhancements of efficient three-party password-based key exchange scheme［J］. International Journal of Communication Systems， 2013， 26（5）：674-686.

［16］XIE Q， ZHAO J， YU X. Chaotic maps-based three-party password-authenticated key agreement scheme［J］. Nonlinear Dynamics，2013， 74（4）： 1021-1027.

［17］YANG J H， CAO T J. Provably secure three-party password authenticated key exchange protocol in the standard model［J］. Journal of Systems and Software， 2012， 85（2）： 340-350.

［18］YOON E J， JEON I S. An efficient and secure diffie-hellman key agreement protocol based on chebyshev chaotic map［J］. Communications in Nonlinear Science and Numerical Simulation， 2011，16（6）： 2383-2389.

［19］ZHAO F， GONG P， LI S， et al. Cryptanalysis and improvement of a three-party key agreement protocol using enhanced chebyshev polynomials［J］. Nonlinear Dynamics， 2013， 74（1/2）： 419-427.

［20］ZHAO J J， GU D W. Provably secure three-party password based authenticated key exchange protocol［J］. Information Sciences， 2012，184（1）： 310-323.

［21］ZHANG L. Cryptanalysis of the public key encryption based on multiple chaotic systems［J］. Chaos Solitons & Fractals， 2008， 37（3）：669-674.

［22］MANGARD S， OSWALD E， STANDAERT F X. One for all-all for one： unifying standard differential power analysis attacks［J］. IET Information Security， 2011， 5（2）： 100-110.

［23］MESSERGES T S， DABBISH E A， SLOAN RH. Examining smart-card security under the threat of power analysis attacks［J］. IEEE Transactions on Computers， 2002， 51（5）： 541-552.

［24］KUMARI S， KHAN M K. Cryptanalysis and improvement of ‘a robust smart-card-based remote user password authentication scheme'［J］. International Journal of Communication Systems， 2014，27（12）： 3939-3955.

［25］WANG D， MA C G， WANG P， et al. Robust smart card based password authentication scheme against smart card security breach［R］. Cryptology ePrint Archive， 2012.

［26］KOCAREV L， LIAN S G. Chaos-based cryptography： theory，algorithms and applications［M］. Berlin：Springer， 2011.

吴凡（1981-），男，山东济宁人，厦门理工学院讲师，主要研究方向为信息安全和网络协议。

廖俊国（1972-），男，湖南衡阳人，博士，湖南科技大学教授、硕士生导师，主要研究方向为网络与信息安全。

Efficient three-party authenticated key agreement protocol based on chaotic map

LI Xiong1， WU Fan2， LIAO Jun-guo1， LIU Yu-zhen1

（1. School of Computer Science and Engineering， Hunan University of Science and Technology， Xiangtan 411201， China；2. Department of Computer Science and Engineering， Xiamen Institute of Technology， Xiamen 361021， China）

Chaotic map has been used in the design of key agreement protocol due to its excellent properties. In most of password three-party authenticated key agreement protocol based on chaotic map， the server needs to store a sensitive password table. It makes these protocols vulnerable to some password related attacks. Besides， it would be dangerous if the password table was leaked. To resolve the aforementioned problems， a new password three-party authenticated key agreement protocol based on chaotic maps was proposed. The server didn't need to maintain a password table， so the proposed scheme was free from password related attack. Compared with other related protocols， the proposed protocol not only enhances the security， but also improves the efficiency greatly.

chaotic maps， key agreement， authentication， password

TP 309

A

10.11959/j.issn.2096-109x.2016.00060

2016-05-14；

2016-06-03。通信作者：李雄，lixiongzhq@163.com

国家自然科学基金资助项目（No.61300220）；湖南省教育厅一般基金资助项目（No.15C0545）；福建省高校杰出青年科研人才培育基金资助项目；福建省中青年教师教育科研基金资助项目（No. JA14369）

Foundation Items： The National Natural Science Foundation of China（No.61300220）， Scientific Research Foundation of Hunan Provincial Education Department （No.15C0545）， University Distinguished Young Research Talent Training Program of Fujian Province， The Education Scientific Research Project for Young Teachers of Fujian （No. JA14369）

李雄（1984-），男，土家族，湖南张家界人，博士，湖南科技大学副教授、硕士生导师，主要研究方向为信息安全和密码学。

刘玉珍（1979-），男，山东单县人，博士，湖南科技大学讲师，主要研究方向为密码学、智能计算。