一类三阶有理差分方程解的全局行为

廖百安，骆元媛

(西华大学理学院，四川 成都　610039)



·基础学科·

一类三阶有理差分方程解的全局行为

廖百安，骆元媛*

(西华大学理学院，四川 成都610039)

主要研究一类有理差分方程在参数取不同值情况下的奇点集和全局行为。通过变换和替换将该方程转化为Riccati方程进行求解，并证明了该方程的解最终将收敛到零或者非零不动点或者是无界的。

差分方程；Riccati方程；奇点集；全局行为

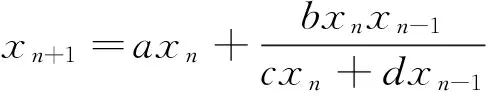
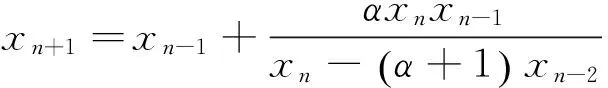
(1)

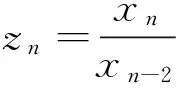
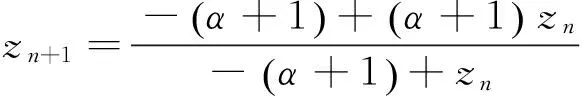
(2)

来求解。我们称方程

(3)

为Riccati方程[10]，这里a,b,c,d为给定实数，初始值z0为任意实数。Grove等在文献[11]中讨论了Riccati方程的二周期解及奇点集等性质。由此可知，方程(2)是Riccati方程，于是，我们根据Riccati方程的性质来求解方程(1)的解。

1　相关定义及引理

定义1方程(1)的奇点集是所有(s1,s2,…sk+1)∈Rk+1的点所构成的集合，其中点(s1,s2,…sk+1)满足：当(x-k,x-k+1,…x0)=(s1,s2,…sk+1)时，xm∈I,m=0,1,…,n-1,但xm+1∉I，即方程(1)的奇点集是所有使得其右端不能被定义的初始值的集合。

引理1[11]下列结论成立。

1)方程(3)有最小二周期解当且仅当b+c=0。

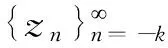
3)当b+c=0时，方程(3)的奇点集为F={-c/d}，当d(bc-ad)=0时，奇点集为空集。

2　主要结论

定理1设α≠0,α≠-1，则差分方程(1)的奇点集为F=s1∪s2，

其中

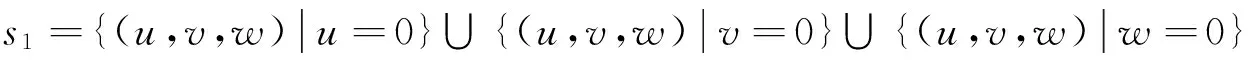
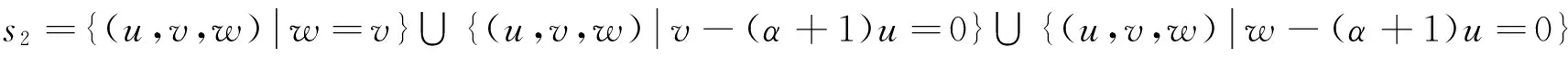
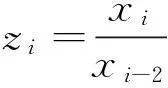
下面我们讨论当α∈R(α≠0,α≠-1)，方程(1)解的最终走向。

定理2设α≠0,α≠-1，则差分方程(1)对任意的初始值(x-2,x-1,x0)∉F。

其中

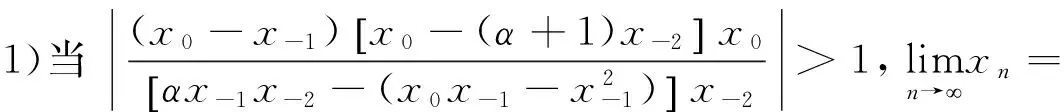
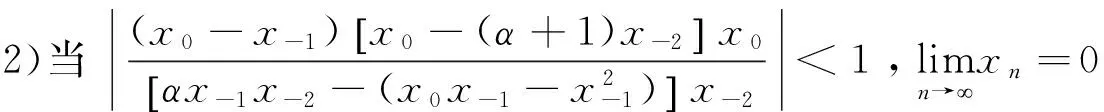
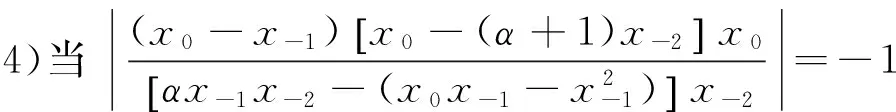
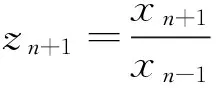
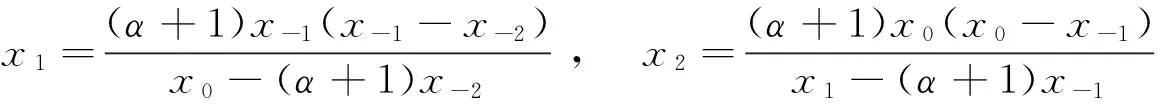
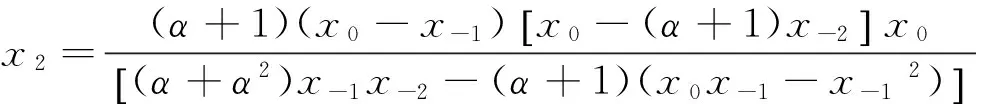
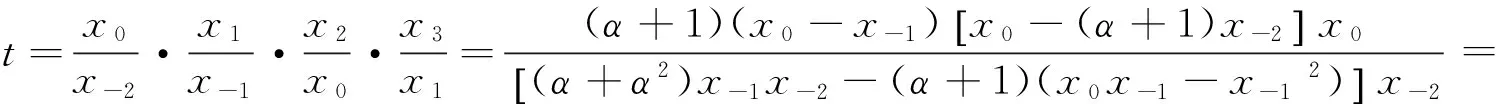
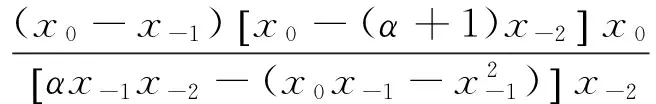
综上所述，

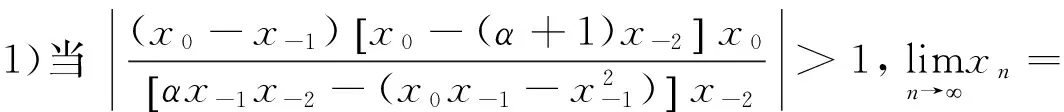
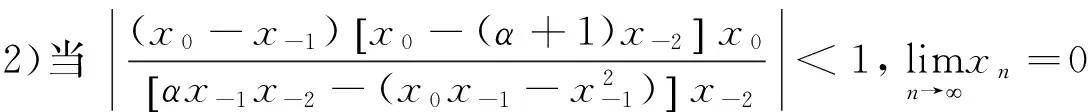
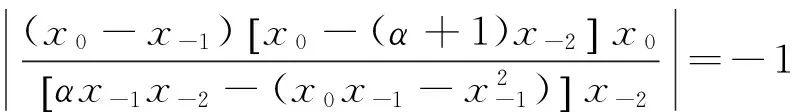
[1]Hartman P, A Wintner. On Linear Difference Equations of the Second Order[J].Amer Math,1950,72:124.

[2]张广,高英.差分方程的振动理论[M].北京:高等教育出版社, 2001.

[3]Amleh A M,Camouzis E, Ladas G. On The Dynamics of a Rational Difference Equation Part1[J].International Journal Difference Equations,2008,3:1.

[4]Amleh A M,Camouzis E, Ladas G. On The Dynamics of a Rational Difference Equation Part2[J].International Journal Difference Equations,2008,3:195.

[5]Gamouzis E, Ladas G. Dynamics of Third Order Rational Difference Equations with Open Problems and Conjectures[M]. Boca Raton:Chapman and Hall/CRC Press, 2007.

[6]Gamouzis E, Papaschinopoulos G. Global Asymptotic Behavior of Positive Solutions On The System of Rational Difference Equations[J]. Appl Math Lett,2004,17:733.

[7]Elsayed E M. Qualitative Behavior of a Rational Recursive Sequence[J].Indag Mathem N S,2008,19(2):189.

[8]Dehghan M, Kent C M, Mazrooei-Sebdani R,et al. Sedaghat H Monoteone Oscillatory Solutions of a Rational Difference Equation Containing Quadractic Terms[J].Difference Equ Appl,2008,14:1045.

[9]Sedaghat H.Global Behaviors of Rational Difference Equations of Orders Two and Three with Quadractic Terms[J].Difference Equ Appl,2009,15:215.

[10]张景中,杨路,张伟年.迭代方程与嵌入流[M].上海:上海科技教育出版社,1998.

[11]Grove E A, Ladas G. Periodicities in Nonlinear Difference Equations[M]. Boca Raton:Chapman and Hall/CRC Press, 2005.

(编校：叶超)

Global Behavior of a Third Order Rational Difference Equation

LIAO Baian, LUO Yuanyuan*

(SchoolofScience,XihuaUniversity,Chengdu610039China)

In this paper, we mainly studied forbidden sets and global behavior of a third order rational difference equation in the case of different parameters. We converted the equation into a Riccati equation, and proved that the solutions of the equation eventually converge to zero or non-zero fixed point or unbounded.

difference equation；Riccati equation；forbidden set；global behavior

2016-04-14

四川省教育厅项目(SJG2014006)；西华大学研究生创新基金(ycjj2015169)；西华大学科研项目(Z1513322)。

骆元媛(1986—)，女，讲师，博士，主要研究方向为数论及微分方程。E-mail：289028774@qq.com.

O175

A

1673-159X(2016)04-0035-4

10.3969/j.issn.1673-159X.2016.04.007