基于变分狄利克雷模糊核估计的行车记录盲图像复原

杨　伟，谢维成*，石林玉

(1.西华大学电气与电子信息学院，四川 成都　610039；2.四川省信号与信息处理高校重点实验室，四川 成都　610039)



·计算机软件理论、技术与应用·

基于变分狄利克雷模糊核估计的行车记录盲图像复原

杨伟1、2，谢维成1、2*，石林玉1、2

(1.西华大学电气与电子信息学院，四川 成都610039；2.四川省信号与信息处理高校重点实验室，四川 成都610039)

针对行车记录模糊图像的模糊核不能准确估计的问题，提出一种变分狄利克雷分布的模糊核估计方法，并利用改进的增广拉格朗日算法实现有效的图像复原。采用梯度投影法求解优化问题，提取图像边缘的精确方向，用狄利克雷分布替代模糊后验估计消除图像噪声，减少额外约束；以超拉普拉斯先验分布建模，结合ALM实现行车记录盲图像复原。实验结果表明，通过多尺度的模糊核估计，能有效估计模糊核并消除行车记录图像的噪声，恢复行车记录图像的纹理细节。与其他方法相比较，所提出的盲图像复原方法，从视觉特性和评价指标来讲都具有较好的恢复效果。

盲图像复原；图像去模糊；狄利克雷分布；增广拉格朗日法；超拉普拉斯

盲图像复原指的是在点扩散函数PSF(模糊核)未知的情况下从退化的模糊图像中恢复出图像的细节信息。它是模式识别、图像处理、计算机视觉等的基础，在医学诊断、刑侦分析、安全监控、卫星遥感等领域有着广泛的应用。盲图像复原包含2个关键因素：模糊核的估计、隐含图像的估计。高速行驶车辆的行车记录仪拍摄的图像的复原就属于盲图像复原的范畴。车辆在行驶过程中难免会因抖动、高速行驶，导致行车记录仪拍摄的图像模糊，驾驶人员的视觉定位失效；因此，行车记录模糊图像的盲复原显得尤为重要。

最早的盲图像的去模糊算法[1]可以追溯到上世纪70年代，而后相继出现了大量相关算法[2-4]；但这些算法在速度与效果上都没有达到令人满意的结果。Fergus等[5]用统计学习的方法进行模糊核估计，该算法速度慢、对含噪的降质图像不能准确估计其模糊核，且容易产生振铃效应。Babacan等[6]利用变分贝叶斯方法，提出了超高斯先验框架。Levin等[7-8]分析了基于MAP的模糊核估计失效的原因，提出MAPh方法,即边缘化所有隐含图像后，用最大后验概率单独估计模糊核h，但该方法仍不能完全准确估计模糊核。对模糊核估计起决定作用的是图像的边缘信息，而图像细节信息的作用较小。Cho等[9]提出利用双边滤波器(Bilateral Filter)、冲击滤波器及梯度幅度取阈值对图像边缘进行预测，此算法去模糊质量较高、速度较快，但对模糊核估计仍不够准确。Sun等[10]提出一种新的参数化图像块模型，归一化图像的阶跃边缘，使用图像统计学习、综合模型以及定向滤波器进行处理，对模糊核估计的准确性有了提高，但仍存在估计偏差。

本文针对行车记录的运动模糊图像进行盲复原，主要在模糊核估计和隐含图像估计方面做了改进，将超拉普拉斯法应用于盲图像复原中，并结合变分狄利克雷方法对模糊核进行估计。在模糊核的估计方面，采用变分狄利克雷方法[11]，使优化问题不需要任何等式约束，用梯度投影法求解优化问题，提取图像边缘的精确方向，从而较准确地估计模糊核。在隐含图像的估计方面，通过改进的增广拉格朗日算法[12]处理不确定的边界条件，以提高估计图像的质量和算法的运行速度。实验结果显示，本文的方法对于盲图像复原具有较好的恢复性能。

1　模糊核估计

1.1数学模型

在实际应用中，对于从行车记录中得到的运动模糊图像，假设其退化过程是线性的，具有空移不变性，成像系统的降质过程可以用卷积模型模拟

y=H*x+n。

(1)

式中：x是原始图像；H是卷积矩阵；n是零均值的高斯白噪声；*表示卷积运算；y表示降质图像。

本文采用正则化的方法解决行车记录的盲图像复原过程中的病态问题，通过增加对x和h的额外约束解决行车记录盲图像复原中的病态问题，用交替迭代的方法对x、h进行优化。

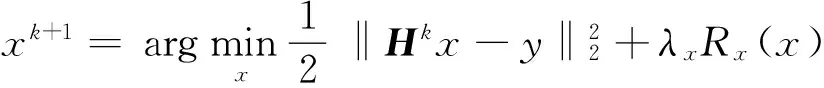
(2)

(3)

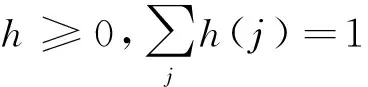
(4)

式中：k表示迭代的次数；Hk是对h的第k次迭代的模糊估计脉冲响应形成的卷积矩阵；Xk+1是由恢复图像xk+1形成的卷积矩阵；Rx和Rh为正则化函数；λx>0和λh≥0控制数据拟合项与正则化项平衡的“惩罚”权值；iXk+1为图像xk+1第i次滤波形成的梯度矩阵。

1.2变分狄利克雷模糊核估计

求解精确的模糊核h是相当困难的，本文使用狄利克雷分布对PSF进行约束。变分狄利克雷方法是一种与图像相关的稀疏性自适应的方法，它可以有效地消除模糊核噪声，增加模糊核估计的准确性。

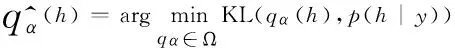
(5)

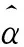
L(α)=γ(α-1)·(ψ′(α)-ψ′(Sα))+

(6)

L(αp)≤L(α)+δ1(αp-α)TL(α)。

(7)

如果αp不存在，则减小步长为s=s·δ2，直到满足不等式(7)为止，将梯度投影应用于模糊核估计中，其算法如图1所示，以lb=1,γ=10-6作为默认值。对于模糊核的估计，采用变分狄利克雷的方法可以防止数据的过拟合，改善变分贝叶斯估计中复原图像产生的振铃效应。

输入数据:清晰图像x',已知模糊核k'1.图像预处理用模糊核k'对图像x'进行卷积并加入噪声n,得到模糊图像y2.模糊核估计核初始化:利用高斯低通滤波生成一个掩膜,作为初始核k1核优化: fori=1:N(N表示金字塔层数) forj=1:M (1)利用梯度投影算法求解方程(6)得α (2)利用式子(5)结合h=α/Sα求得模糊核 (3)将本层得到的模糊核加入下层迭代中 end end3.非盲图像去模糊由第二步得到的模糊核,对模糊图像y去模糊。输入参数μ,βx,βy,βt,设置参数ρr(默认值为2),τ0(默认值为0.7)初始化:x0=y,u0=Dx0,η=0,k=0,计算矩阵FDx[]、FDy[]、FDt[]、FH[]利用双边滤波器对模糊图像y进行滤波,抑制噪声,保留图像细节While‖xk+1-xk‖2/‖xk‖2≤tol(1)用式子(11)结合方程(14)(15)求解子问题x(2)用式子(12)结合方程(16)求解子问题u(3)用方程(13)结合求得的x、u更新拉格朗日乘子η(4)用式子(9)更新ρrEnd输出:去模糊图像

图1算法总体流程

2　基于改进增广拉格朗日算法的快速图像复原

2.1增广拉格朗日算法

由方程(1)可知，盲图像复原是对逆问题的求解，具有病态性。为解决逆问题的病态，将改进的增广拉格朗日算法(ALM)用于解决全变差正则化。ALM算法中原有的全变差正则化模型被线性二次代价函数替代，在迭代过程中参数固定不变，无须选择过大的惩罚参数，提高了数值求解的稳定性。

增广的拉格朗日(augmented Lagrangian)方程的数学表达式为：

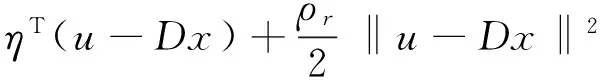
(8)

(9)

2.2算法改进

针对以上问题，本文采用超拉普拉斯先验分布建模并结合增广的拉格朗日算法(ALM)进行求解，数学模型为

(10)

其中乘数η是一个中间向量，它能够保证式(10)的收敛性。模型(10)可以通过以下方法迭代求解：

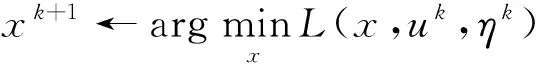
(11)

(12)

ηk+1←ηk-ρr(u-Dixk+1)。

(13)

对于x子问题，通过减少迭代次数k，可以将对方程(11)的求解等价为

(μHTH+ρrDTD)x=μHTy+ρrDTu-DTy。

(14)

模糊核矩阵H是一个三重的块循环矩阵，通过三维离散傅里叶变换(DFT)对角化，方程(14)可通过式(15)求解。

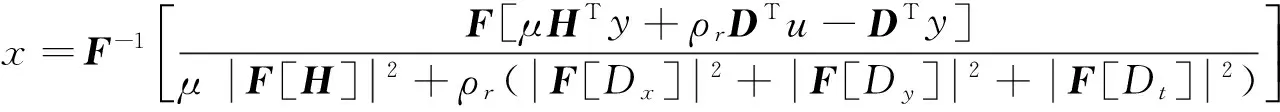
(15)

其中F表示三维傅里叶变换运算。

对于u子问题，固定x、η，方程(12)可以用收缩公式求解。vx=βxDxx+(1/ρr)yx。vy、vt的表达式与vx的表达式类似。ux的表达式为

(16)

同理uy、ut的表达式与ux的表达式类似。通过迭代更新x、u值，由式(13)更新η的值。交替迭代得到对原始图像x的最优估计。

2.3多尺度迭代优化

为处理大的运动模糊，本文通过多尺度方法[5]进行模糊核估计。利用金字塔迭代方式[14]，逐步深入地对模糊核进行估计，直到得到最佳模糊核。1)通过对模糊图像降采样得到金字塔的每层，B0为最高层，B7为最底层；2)使用上文提到的模糊核(初始为3×3)估计的方法在底层B7估计最优核；3)对上层由改进算法计算的清晰图像通过双线性插值上采样为下层的初始图像，对上层估计的模糊核由双线性插值上采样下一层的初始模糊核，层间过渡是分别对低层的清晰图像及估计的核进行上采样得到；4)通过每层迭代求解对模糊图像最优估计的模糊核。本文设置每层迭代的次数为5，每层的模糊核尺寸分别为3、5、9、13、19、27、39、51。采用多尺度方法估计模糊核可以减轻盲图像复原的病态问题。

2.4算法实现

本文通过变分狄利克雷算法进行模糊核估计，在得到模糊核之后，用改进的增广拉格朗日算法对图像进行非盲去模糊。

2.4.1正则化参数μ的选择

正则化参数μ的设置是为了防止数据的过度拟合，μ过大虽然能得到清晰的复原图像但同时会使噪声加剧；μ过小虽然引入的噪声较小，但是复原的图像会产生块效应，使复原图像的质量降低。通常情况下合理的μ的取值范围在[103,105]之间[12]，图2为选取不同μ值图像的复原结果，该head图像为280×280像素，模糊核的大小为17×17。

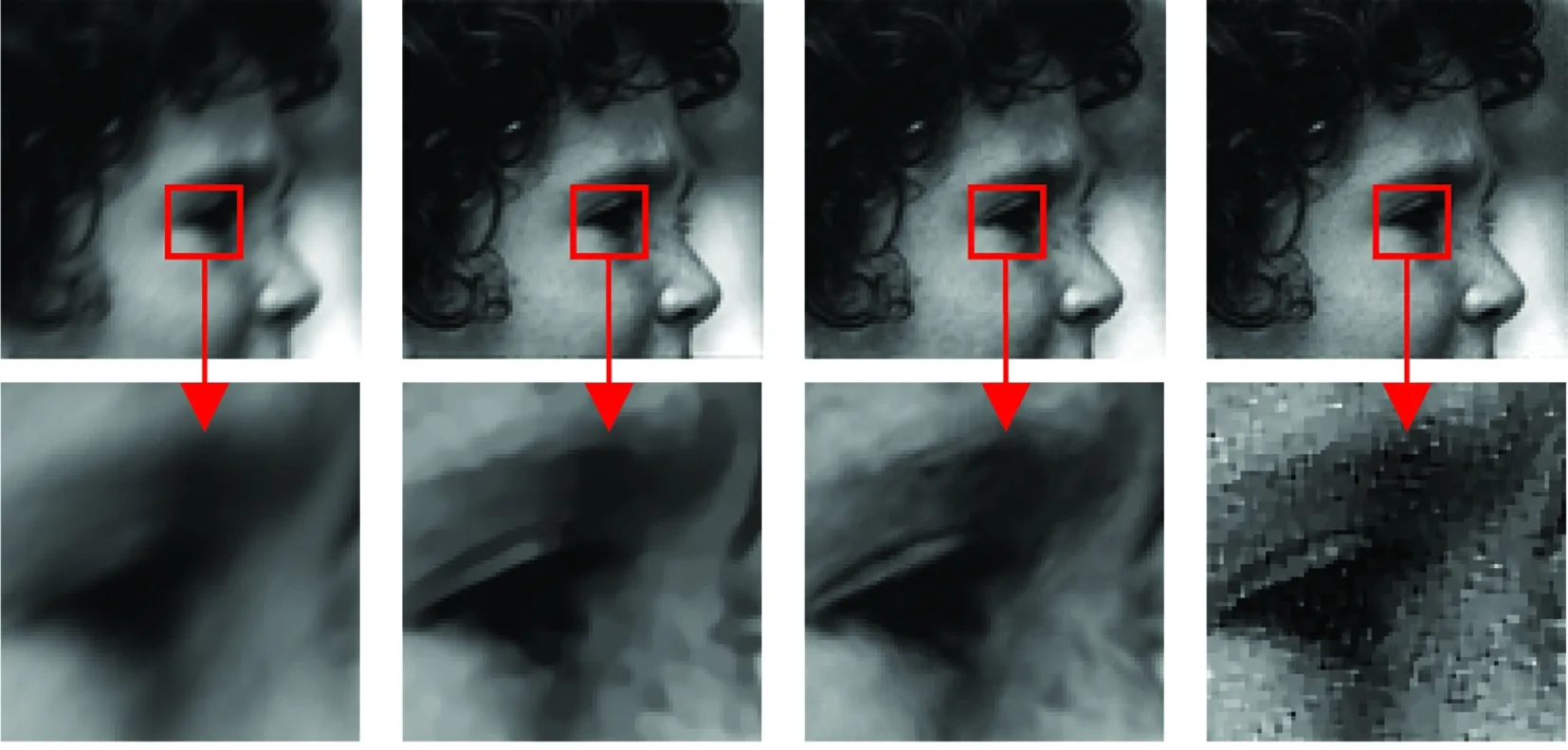
模糊图像μ=103μ=104μ=105

图2不同μ值图像的复原结果

由以上结果可知，μ=103时图像块效应严重，μ=105时产生了噪声干扰，故μ的取值为104最佳。

2.4.2正则化参数ρr的选择

通过式(9)知，选择合适ρr值，可以提高代价函数的收敛速度。若代价函数不收敛会使复原的图像产生振铃效应；代价函数收敛速度越快，算法的执行效率越高。在约束条件‖uk+1-Dxk+1‖2≥τ‖uk-Dxk‖2中定义了常数τ。通常情况下，在初始的目标函数μ‖Hx-y‖2+‖u‖1中添加

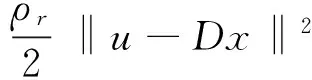
(17)

可以保证函数为凸函数，然而，在一些特定的情况下，随着迭代次数的增加，式(17)并不会下降；因此，设定合适的ρr值确保式(17)是递减的。初始的ρr值在[2，7]之间较为合适[12]。ρr值过大会使目标函数过凸，使得初始问题无法求解；ρr值过小，使得‖u-Dx‖2可忽略不计。对式(9)的分析可知，当0<τ<1,γ>1时，目标函数递减。当τ取0.7[12]，γ取2时，在ρr取不同值情况下对head图像的目标函数的处理过程收敛性影响如图3(a)所示。可以看出，当ρr为2时目标函数收敛速度快，故ρr取2。固定ρr=2，τ=0.7，在不同的γ值的情况下，图像head目标函数的收敛性，如图3(b)所示。

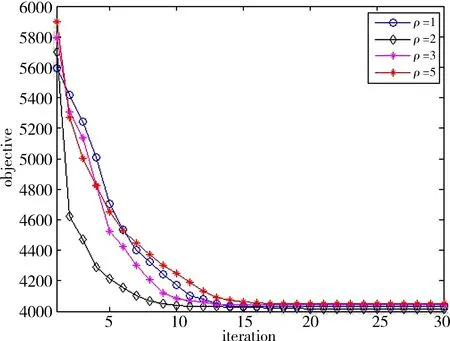
(a)ρr取不同值时目标函数的收敛性

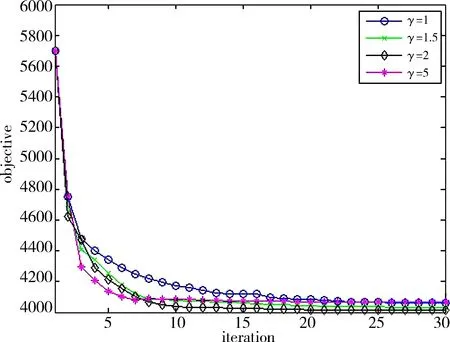
(b)γ取不同值时目标函数的收敛性图3　图像head的目标函数收敛性

由图3(b)可知，当γ取2时算法的收敛效果最好，故在讨论ρr的取值时，设定γ为2可以验证其收敛性。本文算法的总体的流程如图1所示。算法中以‖xk+1-xk‖2/‖xk‖2≤tol为迭代终止条件，其中tol为较小的正数，其值设置为0.001。

3　实验结果与分析

为验证本文算法对高速行驶汽车上的行车记录仪拍摄的运动模糊图像去模糊的有效性，以levin的图像数据库[7]为依据，进行图像去模糊的模拟实验。在实验中，用初始核对原始参考图像进行模糊处理，模拟实际行车记录仪捕获的图像并增加了sigma=0.001的随机噪声。该图像库中包含3幅参考图像，8个初始的运动模糊核，32幅模糊图像。对32幅模糊图像进行了测试，其中4幅模糊图像在不同算法中的恢复效果，如图4所示，图像像素为255×255。为客观地评价本文的算法与其他算法的去噪效果，以误差比率(errorratio)、峰值信噪比(PSNR)、结构相似度(SSIM)作为图像质量的评价指标，其结果如表1—3所示。

图4示出4种算法与本文算法的处理结果。可以看出，本文算法所估计的模糊核更为准确，所得到的去模糊图像也更为清晰，几乎没有振铃效应。表1中的errorratio用以判定模糊核估计的准确性，一般情况下errorratio>3被认为估计失败[7]。通过对32幅模糊图像进行测试(表1仅给出了一部分实验数据)，文献[9]的算法结果中有10个数据大于3，即10个模糊核估计失败，文献[5]的算法结果中有7个模糊核估计失败，文献[7]的算法结果中有4个模糊核估计失败，文献[10]的算法结果中有2个模糊核估计失败，本文算法的errorratio均小于3。表2的PSNR用以衡量恢复图像与参考图像相比较的失真程度。当PSNR值高于28时，图像质量差异不太明显。由表2可知，本文算法估计的图像的PSNR值较其他算法高，图像的失真程度低，具有更多的图像细节信息。表3的SSIM表明恢复图像与参考图像的结构相似度，从图像的组成方面解释图像的结构信息。由表3可知，本文算法得到的图像更好地保持了图像的结构信息，恢复的图像轮廓清晰、层次分明。综合以上分析可知，应用本文算法，图像去模糊的效果更好，得到的细节更丰富，将其应用到行车记录模糊图像的恢复中可以得到高清晰的行车记录图像。

以上各行分别为参考图像、模糊图像、Cho&Lee[9]、Fregusatall[5]、Levinatall[7]、Sunatall[10]、Proposed(本文算法处理后的图像)。

图4　算法对比效果图表1　以error ratio为评价指标针对图2中不同算法的结果

表2　以PSNR为评价指标针对图2中不同算法的结果

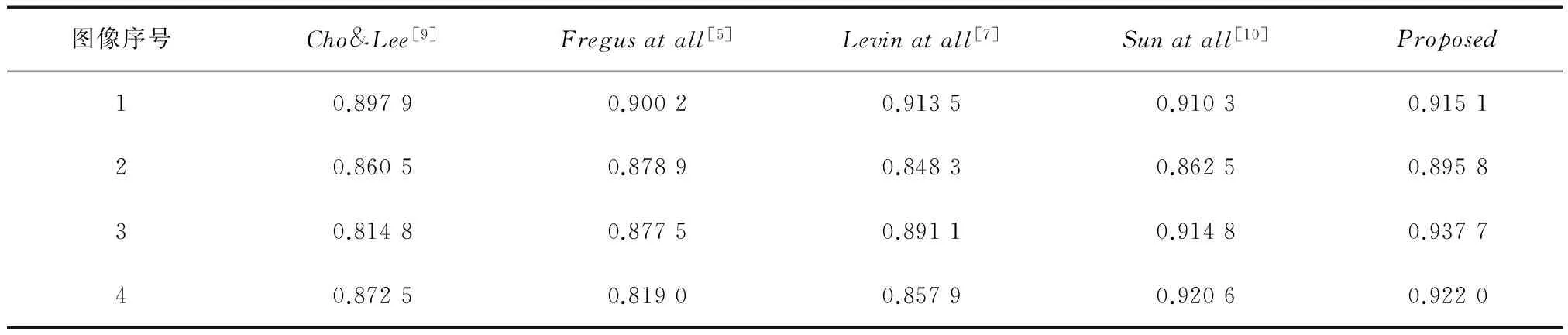
表3　以SSIM为评价指标针对图2中不同算法的结果

4　本文算法在行车记录图像中的应用

为验证本文算法的有效性，对高速行驶汽车的行车记录仪拍摄到的不同运动模糊图像应用该算法进行盲图像复原。实验对8幅行车记录仪拍摄的背景复杂度不同的运动模糊图像进行处理，图像像素为255×255。图5为应用变分狄利克雷分布对图6中行车记录仪拍摄的模糊图像估计的模糊核。图6为盲图像恢复结果。

图5估计的模糊核

由图6可知：对于背景复杂的image#2、3、4、5、6、7，采用该算法，能够有效地对行车记录图像进行去模糊且不会产生振铃效应；对于背景相对简单的image#1、8，其去模糊效果明显，路标清晰可见；对于存在较大的运动模糊的行车记录图像image#5、6、7、8，采用该算法也能够准确地估计出模糊核，去除大的运动模糊，恢复出图像更多的细节信息。由此可见，本算法对于各类运动模糊图像都能准确估计其模糊核，进行有效的盲图像复原，解决视觉定位失效的问题。

5　结论

本文结合狄利克雷分布和增广的拉格朗日算法，利用超拉普拉斯分布进行约束，提出一种基于狄利克雷模糊核估计的盲图像复原方法，在有效恢复图像，去除模糊的同时丰富了图像的细节，保持了图像的边缘信息。最后通过对比实验和各项评价指标验证了该算法的有效性。

[1]Stockham T G, Cannon T M, Ingebretsen R B. Blind Deconvolution through Digital Signal Processing[J].Proceedings of IEEE, 1975, 63(4): 678.

[2]Ayers G R, Dainty J C. Iterative Blind Deconvolution Method and its Applications[J].Optics Letters, 1988, 13(7): 547.

[3]Schultz T J. Multiframe Blind Deconvolution of Astronomical Images[J]. Journal of the Optical Society of America A, 1993, 10(5):1064 .

[4]Michailovich O, Adam D. A Novel Approach to the 2-D Blind Deconvolution Problem in Medical Ultrasound[J].IEEE Transactions on Medical Imaging, 2005, 24(1): 86.

[5]Fergus R, Singh B, Hertzmann A, et al. Removing Camera Shake from a Single Photograph[J]. Acm Transactions on Graphics, 2006, 25(25):787.

[6]Babacan S D, Molina R, Do M N, et al. Bayesian Blind Deconvolution with General Sparse Image Priors[J].European Conference on Computer Vision,2012，7577(1):341.

[7]Levin A, Weiss Y, Durand F, et al. Efficient Marginal Likelihood Optimization in Blind Deconvolution[J]. IEEE Conference on Computer Vision and Pattern Recognition, 2011, 42(7):2657.

[8]Levin A, Weiss Y, Durand F, et al. Understanding and Evaluating Blind Deconvolution Algorithms[J]. IEEE Conference on Computer Vision and Pattern Recognition, 2009, 8(1):1964.

[9]Cho S, Lee S. Fast Motion Deblurring[J]. ACM Transactions on Graphics, 2009,28(5):145.

[10]Sun L, Cho S, Wang J, et al. Edge-based Blur Kernel Estimation Using Patch Priors[C]//Computational Photography (ICCP), 2013 IEEE International Conference on. Cambridge, MA：IEEE，2013：1-8.

[11]Zhou X, Mateos J, Zhou F, et al. Variational Dirichlet Blur Kernel Estimation[J]. IEEE Transactions on Image Processing, 2015,24(12): 5127.

[12]Chan S H, Ramsin K, Gibson K B, et al. An Augmented Lagrangian Method for Total Variation Video Restoration[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2011, 20(11):3097.

[13]Nocedal J, Wright S J. Numerical Optimization[M]. New York, NY,USA: Springer-Verlag, 1999.

[14]Vogel C R, Oman M E. Fast, Robust Total Variation-based Reconstruction of Noisy, Blurred Images [J]. IEEE Transactions on Image Processing, 1998, 7(6):813.

[15]Zhang H, Wipf D. Non-uniform Camera Shake Removal using a Spatially-Adaptive Sparse Penalty[J].in Proc Adv Neural Inf Process Syst, 2013:1556.

(编校：饶莉)

Vehicular Image Restoration Based on Variational Dirichlet Blur Kernel Estimation

YANG Wei1、2，XIE Weicheng1、2*，SHI Linyu1、2

(1.SchoolofElectricalEngineeringandElectronicInformation,XiHuaUniversity,Chengdu610039China;2.SignalandInformationProcessingLaboratoryofUniversity,Chengdu610039China)

When the vehicular image has noise, the estimated blur kernel is not accurate. Therefore a more accurate method based on Variational Dirichlet distribution is proposed to estimate blur kernel, combined with improved augmented Lagrangian to achieve effective image restoration. This method uses the gradient projection method to solve optimization problems and extract precise orientation of the image edge. The Dirichlet distribution substitutes posterior estimate to eliminate image noise and reduce the additional constraint. Hyper-Laplacian prior distribution modeling, together with ALM, is used to restore the vehicular blind image. Experiment results show that multi-scale blur kernel estimator can effectively estimate a blur kernel and eliminate noise of vehicular image, and the texture detail of vehicular image can also be recovered. Compared with other methods, the proposed blind image restoration method have better visual appearances and quality measurements.

blind image restoration； vehicular image deblurring；Variational Dirichlet distribution；augmented Lagrangian method；hyper-Laplacian

2016-02-26

教育部“春晖计划”项目(Z2015115)；四川省教育厅自然科学基金重点项目(15ZA0127)；四川省信号与信息处理高校重点实验室开放基金项目(szjj2015-072)；西华大学研究生创新基金(ycjj2016161)资助。

谢维成 (1973—), 男,教授, 硕士, 主要研究方向为信号检测及信号处理、基于网络的信号检测与控制、智能信息系统开发技术及应用。E-mail:scxweicheng@aliyun.com

TP391.41

A

1673-159X(2016)04-0023-7

10.3969/j.issn.1673-159X.2016.04.005