对2个优化目标要求的离心叶轮入口直径计算模型的分析

严　敬，杨小林，李景悦

(1. 西华大学能源与动力工程学院，四川 成都　610039 ； 2. 流体及动力机械教育部重点实验室(西华大学)，四川 成都　610039)



·机电工程·

对2个优化目标要求的离心叶轮入口直径计算模型的分析

严敬1，2，杨小林1，2，李景悦1，2

(1. 西华大学能源与动力工程学院，四川 成都610039 ； 2. 流体及动力机械教育部重点实验室(西华大学)，四川 成都610039)

提高离心叶轮水力效率与抗空化能力是叶轮设计过程中追求的2项重要技术指标，这2项指标与叶轮进口直径有密切的关系。为实现不同叶轮的性能预期，进口直径应有不同的取值范围。通过对2个叶轮入口直径优化模型的数学分析，阐明叶轮入口直径在不同性能要求下的取值规律，为正确确定叶轮直径提供理论基础。同时，还从不同角度论证了进口直径对叶轮几何形态和水力性能多方面的影响。

离心叶轮；参数优化；理论分析；

离心叶轮进口直径D0是一个重要的叶轮结构参数，叶轮的水力效率和抗空化能力是评价叶轮性能的2项核心指标，D0对这2项指标都有直接的影响。

长期以来，国内泵行业的设计人员都以以下传统公式[1-4]计算确定D0值：

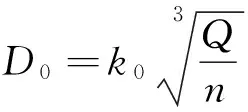
(1)

式中，Q、n分别指泵在设计点的流量与转速，主要考虑提高泵的抗空化能力时系数k0取5.0～5.5，主要考虑提高泵的效率时k0取3.5～4.0，两者兼顾时k0取4.0～5.0。k0的推荐值中含有经验成分，但这些经验值揭示了一重要事实：追求叶轮不同的水力性能指标对D0值的要求是不一样的。本文将通过对2个叶轮进口尺寸优化模型的分析，定性说明为实现不同的叶轮水力性能要求D0有不同的分布规律，由此证明k0的取值范围的理论基础。按不同的要求确定叶轮入口直径这一常识性认识有鲜明的理论基础，通过分析这一公式的理论成因将帮助叶轮设计人员不仅能使用式(1)确定叶轮入口直径，同时对这一常用经验公式有一定的理论认识。

1　对2个离心叶轮入口直径优化模型的分析

1.1以提高叶轮水力效率为目标的优化模型

离心叶轮入口处的主要水力损失为水流进入叶片进口边处的冲击损失，这一局部损失正比于水流在叶片进口处的相对速度水头；但是在叶片进口边上各点处的相对速度并不相等。由于主体水流是在叶轮中间流面附近流过叶轮的，因此，减小叶轮进口边与中间流线交点处的相对速度w1自然成为减小叶轮进口水力损失的主要措施。图1中，将这点记为1，并设这点的直径为D1。

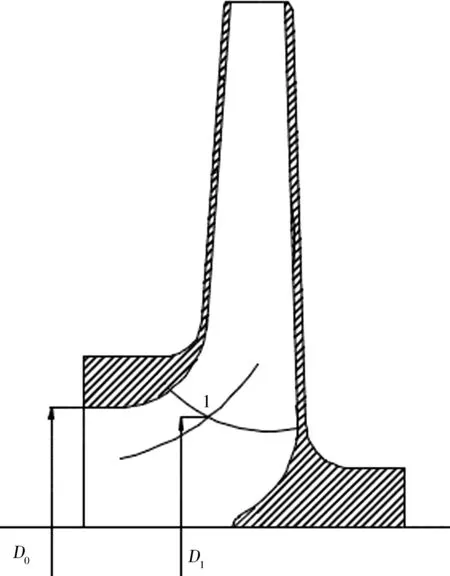
图1　叶轮内最低压力点

为方便，引入k1=D1/D0，一般情况下这是一个小于1的正数。同时引入k2=F0/F1，F0指叶轮入口面积，即πD02/4，F1指通过1点处的轴面液流过水断面有效面积。反映叶轮过水断面面积随轴面流道中线变化规律的曲线在叶轮入口处总是上升的，因而k2也是一个小于1的正数。

除双吸泵等少数例外，水流在叶片入口一般为无预旋的法向方向，由点1处的直角速度三角形，有

w12=u12+vm12。

(2)

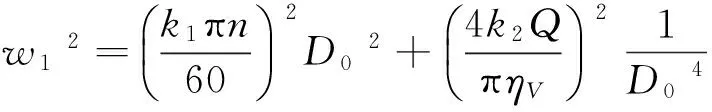
(3)

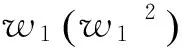
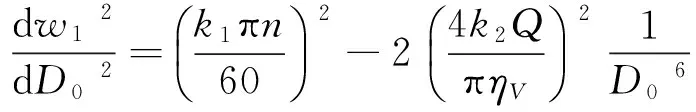
令上式为0，得到

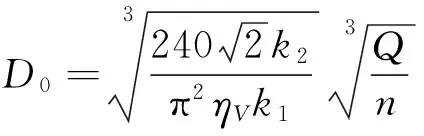
(4)

1.2以提高叶轮抗空化能力为目标的优化模型

叶轮在设计点的必须汽蚀余量Δhr是衡量一台泵的抗空化能力的主要指标，这一值越低，泵发生空化的可能就越小，尽量降低泵的这一值成为叶轮设计中另一重要追求目标。

叶轮的必需气蚀余量定义为单位重量的水在设计点为叶轮入口绝对压力能与动能之和与叶轮内最低压力点绝对压力能之差。由这一定义，利用叶轮中水流相对运动伯努利方程，可导出

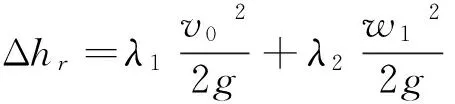
(5)

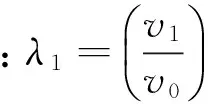
利用式(3)，可将式(5)写成叶轮入口直径D0的函数。

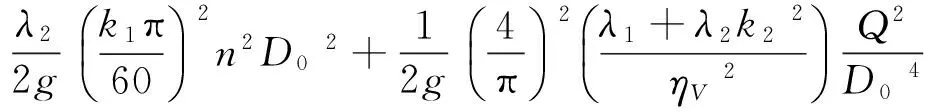
(6)

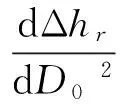
由式(6)，有

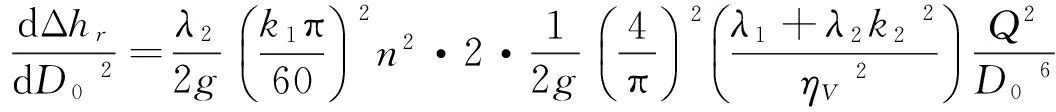
令上式等于0，得到

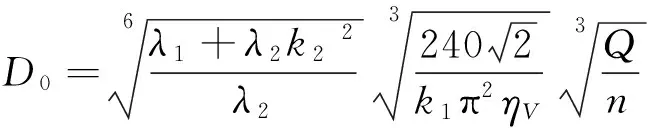
(7)

1.3对2个优化结果的比较与分析

分析结论性的(4)、(7)式后，可以得到以下重要结论。

1)低比转速离心泵有小流量、高扬程的外特性。式(4)、(7)表明，在2种优化结果中，D0都与设计流量Q正相关，所得到的D0都相对较小。另一方面，为产生较高的设计扬程，即使在以降低叶轮直径D2为目标的优化结果中，D2值仍不可能太小；因此，低比转速叶轮的D2/D0比值比一般离心叶轮大，叶轮流道窄长，叶片基本处于径向位置。

2)式(6)表明，泵在设计点的Δhr与设计流量的平方正相关。在用户给定的设计流量过大时，应考虑采用双吸结构保证泵的抗空化能力。

4)上文已说明，在仅从降低叶轮水力损失的目标出发得到的D0应较小，实际上，这一措施也有利于提高泵的容积效率。当叶轮以角速度ω匀速旋转时，泵前泵腔中的水体将以角速度ω/2 像刚体一样绕叶轮轴心线旋转。由于这一旋转水体最下端M点处的压力pM大于叶轮入口压力p0，在压力差pM-p0的作用下，一部分已从叶轮中获取能量的水将从旋转叶轮与静止泵体之间的径向间隙流回叶轮入口，形成容积损失，如图2所示。文献[8-9]证明了如果叶轮出口处压力为常数p2，在泵腔内水体以ω/2角速度匀速旋转条件下，泵腔中任意半径r上压力p与r有以下函数关系：p=p2+ρω2(r2-R22)/8，这里R2为叶轮半径。由此可看出，M点的半径r越小，M点的压力pM就越小，产生泄漏的间隙两端的压力差也随之降低。显然，较小的叶轮入口直径D0决定了r有减小的趋势。同时，泄漏间隙实际上是一个与叶轮轴心线垂直的圆环，这时圆环内半径与面积也将随D0的减小而减小，这2方面的因素综合决定了减小D0值也同时有利于提高泵的容积效率。

图2　叶轮入口处泄漏间隙

5)D0是决定泵抗气蚀能力的一个重要几何参数，应说明，除此之外，泵的气蚀性能还与其他一系列因素有关，如叶轮轴面图上进口边的位置与形状、叶片厚度、沿叶片入口边冲角大小等等。它们对式(5)中的λ1、λ2都将产生影响，前文将这2个值视为常数只是一种近似。

6)泵的必需气蚀余量Δhr是一个随泵工况点变化的变量。叶轮内的最低压力点出现在沿最大冲角流线进入叶片进口边稍后的叶片背面。在小流量工作区，随通过叶轮流量增大，叶片入口处相对速度的方向与叶片方向逐步一致，冲角逐步减小，叶片背面的最低压力值及低压区面积变化不大，Δhr基本为常数；但当叶轮流量超过某一值后，叶片入口相对液流角将大于叶片进口安放角，脱流出现在叶片工作面，随流量继续增大，工作面上进口边稍后处脱流旋涡区压力进一步降低，低压区扩散，Δhr会快速上升[10]。可以看出，为避免泵的空化破坏，应避免泵在超过设计流量情况下长期运行。

2　结束语

本文通过对2个优化离心叶轮进口直径D0的数学模型的分析，以理论方法证明了在对叶轮的水力性能有不同的预期时，D0值应有不同的取值规律，即在主要考虑提高叶轮抗空化能力时的D0值应大于主要考虑降低叶轮入口水力损失时的对应值。在此基础上，本文进一步从几个角度讨论了D0值对叶轮的几何形态及应有结构，叶轮的容积效率及泵合理运行区间的影响。文中所得到的一些结论可为叶轮设计人员及水泵使用人员提供了参考。

[1]丁成伟. 离心泵与轴流泵[M]. 北京：机械工业出版社，1978:104.

[2]查森. 叶片泵原理及水力设计[M]. 北京：机械工业出版社，1988:106.

[3]关醒凡. 现代泵理论与设计[M]. 北京：中国宇航出版社，2011:254.

[4]吴玉林，刘娟，陈铁军. 叶片泵设计与实例[M]. 北京：机械工业出版社，2011:70.

[5]同济大学数学系. 高等数学：上[M]. 6版.北京：高等教育出版社，2009:77.

[6]严敬. 低比转速离心泵[M]. 成都：四川科学技术出版社，1998:61.

[7]王幼民，唐铃风. 低比转速离心泵多目标优化设计[J]. 机电工程，2001，8(1):52.

[8]严敬，赵琴，杨小林. 工程流体力学[M]. 重庆：重庆大学出版社，2007:17.

[9]李景悦，严敬，赖喜德，等.离心叶轮平衡机构轴向力的计算与分析[J]. 西华大学学报(自然科学版)，2015,34(3)：71.

[10]钱涵欣. 水泵水轮机转轮叶片表面压力测试[D]. 北京：清华大学，1985.

(编校：夏书林)

Analysis on Two Centrifugal Impeller Eye Calculating Models in Term of Different Optimum Requirements

YAN Jing1，2，YANG Xiaolin1，2，LI Jingyue1，2

(1.SchoolofEnergyandPower，XihuaUniversity，Chengdu610039China2.KeyLaboratoryofFluidandPowerMachinery，MinistryofEducation(XihuaUniversity)，Chengdu610039China)

Improving hydraulic efficiency and cavitation resistance are two main objects in centrifugal impeller design procedure and both of them are closely pertinent to impeller eye diameter. In design practice, the impeller eye dimension should be determined in different ranges in accordance with varying feature expectation. Based on analysis on two optimum programs associated to eye size, we presented rules to calculate impeller eye dimension for diverse requirements and provide theoretical basis for impeller designers. Moreover, this paper also discussed impacts of eye dimension on impeller geometric size and hydraulic characteristics at different angles. The results can offer beneficial references for impeller design and pump operation.

centrifugal impeller; parameter optimum; theoretical analysis;

2015-06-08

流体及动力机械教育部重点实验室(西华大学)项目(szjj2014-032)；西华大学研究生创新基金项目(ycjj2014179)。

严敬(1947—)，男，教授，硕导，主要研究方向为流体机械过流部件现代设计方法。

TH311

A

1673-159X(2016)04-0071-4

10.3969/j.issn.1673-159X.2016.04.015