朴实蕴灵动 简约显大气——2016年浙江省数学高考数列题赏析*

●王勇强

(湖州市教育科学研究中心　浙江湖州　313000)



朴实蕴灵动简约显大气

——2016年浙江省数学高考数列题赏析*

●王勇强

(湖州市教育科学研究中心浙江湖州313000)

文章通过对2016年浙江省数学高考数列题的呈现、赏析、解法探究、变式以及反思，给出些许教学启示.引导学生重视课本核心概念，重视在新的问题情境中迁移与运用平时积累的数学基本活动经验，引导学生真正参与到数学思维活动中等，予以抛砖引玉，以期对数学教学有所帮助．

数列；概念本质；数学基本活动经验；教学启示

数列是高中数学的核心内容之一,具有丰富的内涵和外延，它可以沟通函数、方程、不等式等内容之间的联系，常受到高考命题者的青睐．2016年浙江省数学高考试卷也对它进行了重点考查，主要考查等差数列和等比数列的概念、通项公式、求和公式等基础知识，考查数列的递推关系与单调性以及与不等式性质之间的联系，同时考查了学生的命题转换、数形结合和分类讨论等数学思想方法以及推理论证能力、分析问题和解决问题的能力．理科卷考查数列知识的具体题目有第6，20题；文科卷第8，17题考查了数列知识(其中文科卷第8题与理科卷第6题完全相同)．其中理科卷的第8题和第20题是其中最为出彩的好题，细细品味，意蕴深远，同时该题也是令大多数考生头疼的考题．笔者认真思考了这2道试题，作一个简要的赏析，用于抛砖引玉．

1　细品概念，朴实灵动

图1

例1如图1，点列{An}，{Bn}分别在某锐角的2条边上，且|AnAn+1|=|An+1An+2|，An≠An+2，n∈N*，|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2，n∈N*(其中P≠Q表示点P与Q不重合)．若dn=|AnBn|，Sn为△AnBnBn+1的面积，则

()

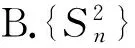
(2016年浙江省数学高考理科试题第6题)

分析粗略一看，感觉本题既抽象又朴实：文字表述较抽象，但所给的图形却是考生在中学学习数学时熟悉朴实的几何图形．本题考查的是平面几何中两点间距离与三角形面积的运算以及抽象概括和推理论证的能力，符合浙江省“重基础，重本质，考查学生数学核心素养”的一贯命题思路．不少考生在考场上感觉无从下手，乱算一气，最后猜一个答案．但若能仔细挖掘，运用数形结合的思想方法，用代数的方法来研究几何问题，可以看出本题蕴含着等差数列概念的几何本质——等差数列的图像是某直线上一群等距且孤立的点，从而顺利找到解题的突破口．

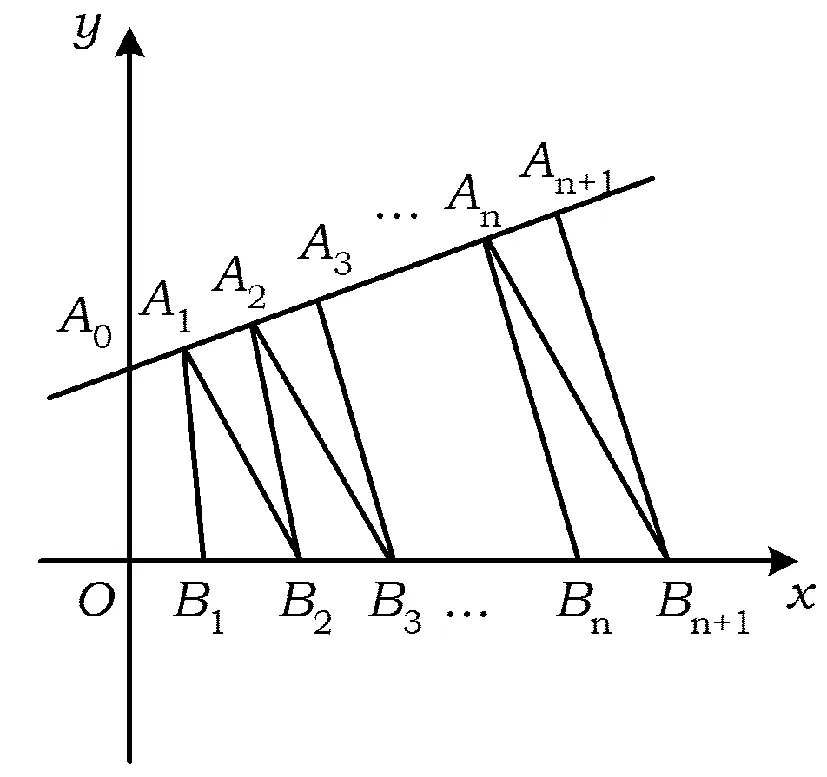
图2

以直线B1B2为x轴，建立如图2所示的坐标系，由|AnAn+1|=|An+1An+2|，An≠An+2，n∈N*这个条件可得：点列{An}的纵坐标成等差数列；由|BnBn+1|=|Bn+1Bn+2|，Bn≠Bn+2，n∈N*可得：{Sn}是等差数列，故选A．当且仅当|AnAn+1|=|BnBn+1|，即AnBn∥An+1Bn+1时，{dn}成等差数列，故选项C不恒成立．因此，深刻理解等差数列的概念，就能找到本质、自然、灵动的解法．

点评以上这道数列选择题考查的重点不是“算”而是“想”．从上面的分析与解题过程看，试题强调数学思维与本质，要求考生深刻理解概念，并能合理转化、灵活运用．在问题的数形转化和对等差数列概念的多元表征中，凸显概念的数学本质．

章建跃先生认为：“从数学角度衡量，‘好题’具有以下‘品质’：与重要的数学概念和性质相关，体现基础知识的联系性，解题方法自然、多样，具有自我生长的能力等；从培养思维能力的角度，‘好题’则应有：问题是自然的，对学生的智力有适度的挑战性，题意明确、不纠缠于细枝末节，表述形式简洁、流畅、好懂等．”[1]

由此，笔者认为理科第6题是一道拥有等差数列几何背景，与重要的数学概念相关，是体现基础知识的联系性，解题方法自然、灵动，体现思维能力的好题.而理科第20题则在经典的递推数列问题中植入新的设问，令人耳目一新．

2　简约大气，锐意创新

1)证明：|an|≥2n-1(|a1|-2)；

(2016年浙江省数学高考理科试题第20题)

评析经典的递推数列问题在浙江省数学高考解答题中反复出现，早些时候曾出现在2004年第22题、2005年第20题、2006年第20题、2008年第22题中，另外2015年也将递推数列问题第20题作为整卷的最后一题．本题主要考查数列的递推关系与单调性以及与不等式性质的联系，同时还考查了学生的命题转换、分类讨论的数学思想方法以及推理论证能力、分析问题和解决问题的能力．该题的文字表述非常简洁、流畅，设问层次递进，数学内涵却很丰富，给人一种简约之中彰显大气的韵味．该题在经典的递推数列问题中加入绝对值，并与不等式结合，从而挖掘出创新的设问，其深刻的数学思想更令人回味．

分析对于第1)小题，若将问题的题干简化为

则可变形为

an+1-2=2(an-2)，

或

于是问题转化为考生熟悉的构造等比数列求通项公式的问题或数列累加求和问题.因此要解决此问题,则需将平时积累的数列求通项、求和的典型数学思维活动经验迁移到含绝对值、不等式符号的创新设问情境中．

下面分别给出解决第1)小题的2种解法：

解法1由题意和绝对值三角不等式知

于是 |an+1|-2≥2(|an|-2),

(1)

当|a1|≤2时，|an|≥2n-1(|a1|-2)恒成立；当|a1|>2时，由式(1)得到|an|>2，从而

于是

|an|-2≥2n-1(|a1|-2)，

故

|an|≥2n-1(|a1|-2)+2>2n-1(|a1|-2).

综上可知，|an|≥2n-1(|a1|-2)．

解法2由题意和绝对值三角不等式知

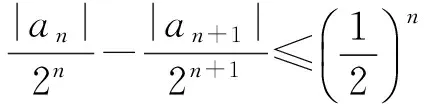
(2)

故

|an|≥2n-1(|a1|-2)．

点评本小题解题所依据的数学基本思维活动经验是“构造等比数列求通项公式的经验或数列累加求和经验”，当然也用到了绝对值三角不等式的性质．这种将“|an|-2”看成整体构造等比数列的基本思维活动经验大多数高三学生都有，解题的关键不是数学基本思维活动经验的积累，而是数学活动经验的迁移与运用，将其迁移运用在“等”到“不等”的新情境，引导和促进学生“再发现”“再创造”新知识[2]，从而顺利解决问题．

第2)小题的分析如下：

从而

(3)

由m的任意性，当m→+∞时，

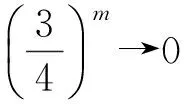
即

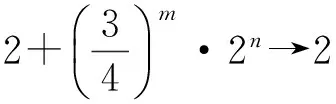
综上可知，任取n∈N*，有|an|≤2．

若将本小题的解题的起点与终点进行调整互换，则可用反证法来解决．

(4)

即

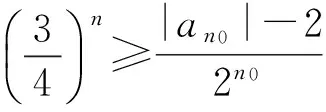
3　教学启示，值得反思

对于经典的数列内容，不少学生看似熟悉，觉得自己已掌握了数列的基础知识、基本技能和基本数学思想方法，也积累了一些基本数学活动经验，认为考试中碰上数列题不会有大的问题，但实际上2016年高考的2道数列题都成为大多数考生头疼的考题．这说明目前的数学教学还存在着一些问题:平时教学没有重视核心概念，学生没有透彻理解核心概念的内涵与外延；没有重视学生对基本数学活动经验的主动运用，相对于积累数学活动经验缺乏对思维活动经验的回顾反思，缺乏在新的情境中对数学思维活动经验的充实深化和主动实践；没有重视将学生如何发现和提出问题、如何独立分析数学问题、如何主动构建研究问题的方法和策略以及如何去掌握解决一些深刻数学问题的基本思想方法等作为主要的教学目标[3]．

若教师能在教学中引导学生重视课本、重视核心概念、重视基本的数学思想方法；重视引导和促进学生主动在新的问题情境中迁移与运用平时积累的经验，并引导学生主动与之前的经验进行对接与融合，再次积累新的数学活动经验用于迁移与内化；重视引导学生真正参与数学思维活动，让学生学习如何读题、分析题意，如何进行多元联系、多角度转化，如何寻找已知与未知的关系去获得解题的思路，那么学生就会养成良好的思考问题的习惯，在转化的意识与方法上有所提高，就会真正提高学习效率．这样也才会使数学教学真正摆脱题海，事半功倍，为学生谋取更广大的长远利益．

[1]章建跃.让学生解好题[J].中小学数学：高中版，2012(10)：封底.

[2]罗新兵，卢恒.数学活动经验的积累与运用[J].中学数学教学参考：高中版，2015(9)：11-14.

[3]王勇强.二次函数永恒的经典[J].数学通讯，2015(11)：24-27.

*收文日期：2016-06-20；2016-07-05

王勇强(1974-)，男，浙江金华人，中学高级教师.研究方向：数学教育.

O122

A

1003-6407(2016)09-38-04