先猜后证：利用数学活动经验实现“问题解决”*

●房香玉　李昌勇　文　东

(四川师范大学数学与软件科学学院　四川成都　610068)



先猜后证：利用数学活动经验实现“问题解决”*

●房香玉李昌勇文东

(四川师范大学数学与软件科学学院四川成都610068)

以学生已有的数学活动经验作为“问题解决”的基础，以“先猜后证”的方式为问题中已知条件与未知结果搭建桥梁；先对问题结果进行“言之有理”的猜，然后再给出“持之有据”的证；这不仅有助于快速找到问题解决的策略，实现“问题解决”，而且还能提升学生已有的数学活动经验，帮助学生养成“化解为证”的问题解决意识，形成一定的数学思维，为学生今后进行更深层次地学习提供准备.

活动经验；先猜后证；问题解决

1　实现“问题解决”的策略

1.1找基础

著名教育家陶行知曾说：“我们要以自己的经验为根，以这经验所发生的知识为枝，然后别人的知识才能接上去，别人的知识才能成为我们知识的一个有机体部分.”舍恩菲尔德在提出的影响“问题解决”的4个要素中把知识资源作为首要因素，他认为知识资源作为解题者解题的根源，如果解题者缺少与原问题解决相关的数学事实、数学定义以及解题技巧，那么该解题活动便很难进行下去[1].而解题者所具有的对原问题相关的数学事实、数学定义以及解题技巧是解题者在以往的数学学习、数学解题等活动中积累起来的经验，即数学活动经验[2].因此，解题者本身已有的数学活动经验便是实现问题解决的基础.

1.2搭桥梁

“先猜后证”是指在问题解决中，解题者可以先抛开问题的某些方面或部分，抓住问题的主要结构，把问题转化成较简单或较特殊的形式，猜测出这个简单或特殊问题的答案，然后利用这个答案的特征来实现更复杂或更一般的问题解决[3].因此，利用这种“先猜后证”的问题解决方式能为已知条件和未知结论搭起桥梁，帮助“问题解决”.当然先猜并不是无根据地乱猜而是以解题者已有的数学活动经验为基础、以直觉为先导、以联想为手段、以逻辑为根据、以观察为向导、以思维为核心进行的合理猜测[4].

那么，解题者在具体问题解决时该如何以自己已有的数学活动经验为基础，以“先猜后证”的方式搭建起已知和未知的桥梁找到“问题解决”的策略呢？下面，笔者结合4个具体的“问题解决”案例来加以分析.

2　“问题解决”的案例分析

图1 　　　　　　　　　　图2 　　　　　　　图3

(2007年全国初中数学竞赛试题)

先猜观察到结论与点B的位置无关，利用极端化的数学活动经验，将点B趋于点C(如图2)，此时线段BP将半圆分成S1,S2+S△ACP这2个部分.注意到S1=S2，故分成的这2个部分面积之差的绝对值就是S△ACP，因此猜测线段BP把图形APCB分成2个部分面积之差的绝对值是S△ACP=4.

分析从极端情况回到一般情况，如图3，联结AP,CP，也有2个弓形S1=S2，因此BP分成的2个部分是S△CBP,S△ABP，只需证|S△ABP-S△CBP|=S△ACP.以圆心O为中心作点M的对称点N，根据等底同高得到

S△CMP=S△ANP，S△CMB=S△ANB,S△PMO=S△PNO,S△BMO=S△BNO，

从而

|S△ABP-S△CBP|=S△PBN，

于是只需进一步证明S△PBN=S△ACP即可.

证明如图3，联结AP,CP，由对称性知S1=S2.作点M关于圆心O的对称点N，则CM=AN,OM=ON,从而

S△CMP=S△ANP，S△CMB=S△ANB，S△PMO=S△PNO,S△BMO=S△BNO,

于是

|S△ABP-S△CBP|=S△PBN=2S△PBO=2S△PCO=S△PCA=4.

反思以极端化的数学活动经验为基础，利用“先猜后证”的解题方式搭建已知条件与未知结论的桥梁，“化解为证”；提升学生变静为动、动中找定的“问题解决”能力，找到定值，进而寻找依据回归定值S△ACP=4，验证猜测，实现问题解决.

(2015年全国初中数学联赛初二试题)

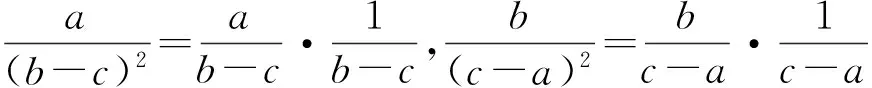
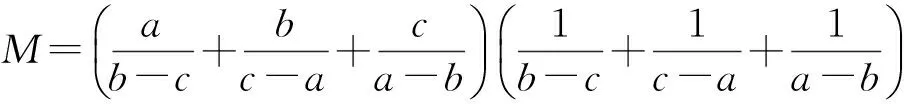
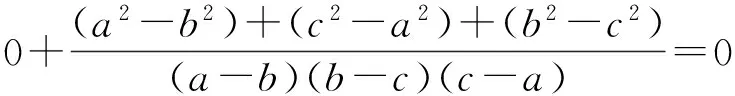
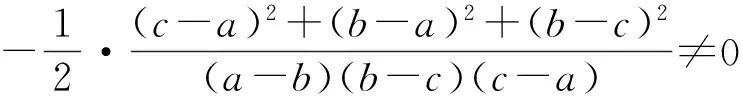
图4

所以

反思“冻结变量，猜测为桥，后证索据”可将很多代数问题化难为易，化繁为简.“冻结变量”不仅能发现剩下变量的关系，更有助于化繁为简；“猜测为桥”以猜测搭起已知与未知之桥，化求为证；“后证索据”以证说理，论证猜测.

例3如图4，在四边形ABCD中，BD是∠ABC的角平分线，∠ADB=45°，∠ACB=90°,求∠DCA的大小.

策略1先猜利用尺规作图的数学活动经验，首先构造出任意∠B及其角平分线，并在∠B的角平分线上任取一点D，过点D作BD的垂线，然后作该直角的角平分线与∠B的一条边相交于点A，这时再过点A作AC⊥BC于点C，联结DC，便可构造出满足条件的四边形ABCD；最后用量角器可测出∠DCA的大小为45°，进而猜测∠DCA=45°.

分析要证∠DCA=45°，只需证明CD是∠ACB补角的角平分线.过点D向AC,BC作垂线,垂足分别为点G,E(如图5)，只需证DG=DE.注意到BD是∠ABC的角平分线，过点D分别向AB,BC作垂线，垂足分别为点H(点H,E重合),F，得到DF=DE，于是只需证DG=DF；通过证明△AGD≌△AFD即可.

证明如图5，过点D分别向BC,AB,AC作垂线，垂足分别是点E,F,G，则DF=DE.注意到

从而∠FAD=∠GAD，于是△AGD≌△AFD，故DG=DF=DE，即直线CD为∠ACE的角平分线，亦即∠DCA=45°.

图5 图6 图7

策略2先猜如图6，将原题目中的Rt△ABC特殊化为等腰直角三角形,则A,B,D在以点C为圆心、BC为半径的圆上，从而

∠ACD=2∠ABD=∠ABC=45°，

故猜测∠ACD=45°.

分析在非特殊化情况下，知∠ACB=90°，作∠ACB的角平分线与BD交于点E，联结AE(如图7)，得到∠ACE=45°.又∠ADB=45°，从而∠ACE=∠ADB，于是点A,E,C,D共圆，得∠ACD=∠AED.进而，通过找到∠AED的大小得到未知的∠ACD的大小.

证明作∠ACB的角平分线与BD交于点E，联结AE(如图7)，则∠ACE=45°=∠ADE,于是点A,E,C,D共圆，从而∠ACD=∠AED.又BE平分∠ABC，则AE平分∠BAC,于是

故∠ACD=45°.

反思策略1和策略2都利用了“先猜后证”的问题解决方式，但2者猜测时所利用的数学活动经验是不一样的.尺规作图的数学活动经验帮助学生思考图形的形成条件，锻炼学生对数学图形的认识和理解能力，对于问题解决更有“活学巧用”的效果；特殊化的活动经验则有助于培养学生从特殊到一般的意识，抓住特殊时的不变性质，发现一般情况的解题策略，加强数学问题解决意识.

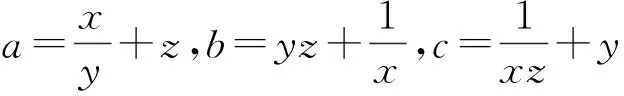
先猜猜测最大数M取最小值的情况是当a=b=c时.注意到当x=y=z=1时，a=b=c=2 ，因此猜测M的最小值为2.

证明根据已知条件知M=max{a,b,c},则M≥a,M≥b,M≥c，于是

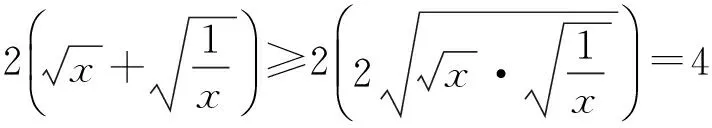
故M≥2.因为当x=y=z=1时，a=b=c=2,所以M的最小值是2.

反思以特殊值为切入点先猜测出问题的答案，然后观察出代数式之间的结构特征，结合已有的数学活动经验证明猜测，这样才能增强学生的数学观察力,提升学生已有的数学活动经验，促进数学思维发展.

以学生已有的数学活动经验作为问题解决的基础，以“先猜后证”的解题方式搭建未知结论和已知条件的桥梁，做出“言之有理”的猜想，帮助学生变求解为证明，从而更有效地找到问题的突破口，发现一般规律,再给出“持之有据”的证明,有效实现问题解决.在数学问题解决中,学生不但要会逻辑分析,而且更应在寻找特例、发现问题结构特征、洞察问题本质时[5],结合自身已有的数学活动经验恰当运用数学猜想，从最简单、最特殊的情况入手,找到问题解决的突破口，增强“问题解决”的能力，从而更有效地立足于新课标中的“四基”，提升数学思维[6].而这种以已有的数学活动经验为基础，结合“先猜后证”的问题解决方式不仅对于学生问题解决能力的培养是非常有帮助的，而且更能帮助学生找到“问题解决”中存在的不变性质，抓住问题的本质，更有效地实现问题解决，帮助知识经验的迁移与获得,这对于学生今后进行更高层次的问题解决的学习是非常有益的.

[1]鲍建生,徐斌艳.数学教育研究导引(二)[M].南京:江苏教育出版社,2013.

[2]仲秀英.学生数学活动经验研究[D].重庆:西南大学，2008:45-56.

[3]喻平.数学问题解决认知模式及教学理论研究[D].南京:南京师范大学，2002:17-21.

[4]傅航.先猜后证的数学思想在高中教学中的应用[J].数学通报,2007(4):38-39.

[5]余锦银.活用特殊化思想巧解数学解答题[J].中学数学,2009(1):16-18.

[6]中华人民共和国教育部.义务教育数学课程标准(2011年)[M].北京:北京师范大学出版社,2012.

*收文日期：2016-05-05；2016-06-10

房香玉(1991-)，四川德阳人，硕士研究生.研究方向：数学教育.

O12

A

1003-6407(2016)09-01-04