三浮陀螺有源磁悬浮位置信号采集电路研究

吴 辽，杨孟兴，王 卿，申志刚，马千里2

（1.中国航天科技集团第十六研究所，西安710100；2.上海磁悬浮交通发展有限公司，上海201204）

三浮陀螺有源磁悬浮位置信号采集电路研究

吴 辽1，杨孟兴1，王 卿1，申志刚1，马千里2

（1.中国航天科技集团第十六研究所，西安710100；2.上海磁悬浮交通发展有限公司，上海201204）

三浮陀螺仪对磁悬浮定中精度提出ε≤0.27μm要求，位移信号采集电路的灵敏度应该高于该要求，电路设计目标定为0.09μm，可以从位置信号采集电路L-R电桥、调理电路和A/D转换电路三部分保证这一目标。给出了两种最佳匹配电阻的估算方法，基于实测电感带入经典公式估算法和电磁仿真软件FLUX估算法，结果表明实验测试的最佳匹配电阻一般高于估算值约30%。推导了调理电路性能指标和A/D转换电路位数与定中精度的关系，结合试验验证了电路设计指标优于0.09μm，完成电路设计任务。

三浮陀螺仪；有源磁悬浮；位置检测；定中精度

0　引言

陀螺仪是惯性导航系统的核心部件之一，由最初的刚体转子支承结构发展到现在的三浮支承技术，即陀螺电机采用动压气浮、浮筒采用液浮和输出轴采用磁悬浮。三浮陀螺由于高精度、长寿命、高可靠性等优点被广泛应用于各类战略武器当中，同时也代表一个国家的惯性技术的发展水平。磁悬浮支承作为三浮陀螺中的关键技术，其主要功能是使陀螺浮子输出轴在空间五个自由度上实现精确定位，同时提供浮子的实时状态信息。

有源磁悬浮由于起动快、精度高、刚度大、干扰小等优点，成为新一代高精度机电陀螺的首选。准确地检测出陀螺浮子的位置状态是有源磁悬浮系统关键技术难题之一，也是保证定中精度的先决条件。目前比较成熟且应用广泛的是L-R检测系统，该系统主要有差分位置信号获取、调理放大、A/D转换三部分，三部分共同决定了检测系统的质量，本文分别从这三部分进行分析设计，保证了电路设计精度优于0.09μm［1-2］。

1　陀螺磁悬浮原理

1.1有源磁悬浮系统组成及工作原理

三浮陀螺仪有源磁悬浮系统由四部分组成，电磁元件部分、输入信号调理电路SIP模块、中心处理电路SOC模块以及输出信号调理电路SIP模块，各部分之间的联系和数据传输关系如图1所示。

图1　径向有源磁悬浮系统框图Fig.1 The system diagram of radial magnetic suspension

从电磁元件结构角度看，有源磁悬浮与无源磁悬浮区别并不大，有源磁悬浮用桥路电阻取代了原来的谐振共作电容，电路由原来的L-C电路变为L-R电路，由于磁路线圈电感L与位置偏移量存在如下关系［3］:

式中，μo为真空磁导率，N为线圈匝数，lfe为铁心磁路长度，l为气隙磁路长度，μr为铁心相对磁导率，S为极弧面积，lg为工作气隙，Δ为偏移量。

当陀螺浮子带着磁悬浮转子发生偏移时，对称位置的磁路电感就会发生变化，引起电感两端存在电压差，检测出这一差分信号，经过调理和A/D转换，进入中心处理电路SOC模块解算、判断和GPIO控制加力电流的通断时间。电磁元件电路即是位置检测的敏感电路又是加力电流的作用对象，必须采用分时控制。一个控制周期一般被分割为位置检测周期、加力周期和恢复等待周期三部分，三部分循环工作，保证陀螺浮子定中精度。

1.2L-R敏感位置偏移量原理

磁悬浮系统工作在位置检测周期时，电磁元件就相当于一个位置传感器，输入量为陀螺浮子的位置偏移量，输出量为桥路电压差，对这一检测关系进行建模，分析与灵敏度和线性度有关的因素。如图1所示，记桥路检测两点电压分别为UA和UB，电源角频率为ω，则:

结合式（2），并记转子没有偏差的情况下电感值为LD，可得带入，化简得:

式（3）反映了原始位置信号和y向偏移之间的量化关系，同样适合x向偏移，此公式可作为控制算法参数标定检验依据。其中，复数K为L-R测量电路的灵敏度，取模对桥路匹配电阻求导可得检测电路最佳匹配电阻的估算公式:

2　L-R桥最佳匹配电阻设计

2.1仿真分析依照上述给出了磁路电感计算公式和最佳匹配电阻估算公式计算出来的最佳匹配电阻与实验测试结果相差很大，因此在电磁仿真软件flux对径向磁悬浮建立2D模型进行仿真分析。将定转子分别定义在不同坐标系，利用两坐标之间的移动来模拟陀螺浮子轴的运动状态，偏移量分解dx、dy、电阻R均参数化设置［4］。

如图1所示连接电路，并将桥路电压差作为检测量。从模型磁场分布和电压输出关系可以判断模型的正确性。图2为径向磁悬浮flux模型，图3为在不同偏移量的情况下输出电压与桥路电阻之间的关系。由仿真结果分析，最佳匹配电阻出现在450Ω附近，此时不同偏移量下的输出电压达到最大，即灵敏度最大（约为9mV/μm）。

图2　径向磁悬浮flux模型Fig.2 The flux modem of radial ABM

图3　输出电压与桥路电阻关系Fig.3 The relation between signal voltage and resistance

2.2实验测试

以径向磁悬浮为例，测试每一条支路的直流电阻和电感值，结合元件设计参数实验测得L′=0.007H，以实验测试结果带入最佳匹配电阻计算公式R′=420Ω，对于径向磁悬浮，选用电阻值为 420Ω、500Ω、600Ω、700Ω、800Ω进行测试。径向磁悬浮检测信号桥路测试结果如表1、图4所示［5］。

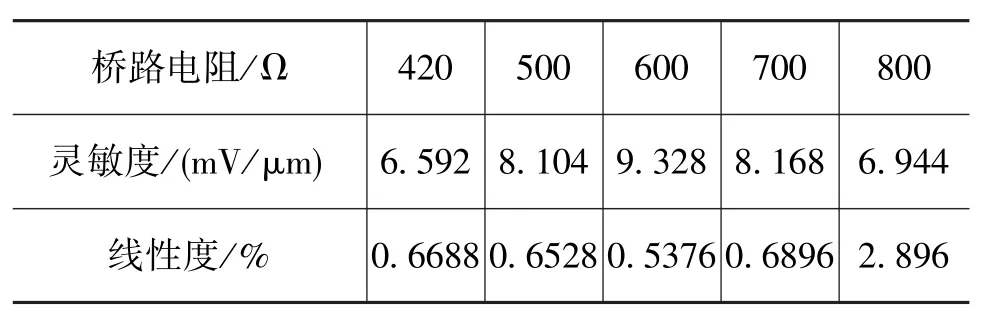
表1　径向磁悬浮检测信号与桥路电阻对比测试Table 1 Comparison test ofradial signal voltage with different resistance

图4　径向磁悬浮检测信号桥路电阻和灵敏度关系Fig.4 The relation between radial resistance and sensitivity

由表1、图4可以看出:该测试方法能够通过位置信号反映出位置的移动方向，可以作为径向有源磁悬浮检测信号的测试方法；桥路的灵敏度和所选桥路电阻的关系如图4所示，灵敏度最大点没有出现在计算的桥路电阻420Ω上，而是出现在600Ω附近；桥路电阻为600Ω时，径向位置信号随位移的灵敏度和线性度都最好，灵敏度为9.328mV/μm，线性度为0.5376%。

2.3对比分析

将通过仿真分析与实验测试两种不同方法所得的最佳桥路匹配电阻以及灵敏度进行对比，具体数据如表2所示。

如表2所示，三种方法的结果存在一定差异:式（1）在对元件线圈电感建模时，将气隙磁路面积等效为极弧面积，随后在忽略铁心损耗磁阻、漏磁和线圈尺寸等因素下得出电感计算理想式（式（2）），在式（2）的基础上得出最佳匹配电阻的理论估算公式，因此理论估算值存在误差是必然的；在flux中仿真分析时，元件的尺寸、材料的性能、电路元件等都是理想的，且二维建模并未考虑径向元件端面的电磁情况，仿真结果也只能作为最佳匹配的估算值；实验测试受实验条件和元件差异等影响，如机械中心不可能和电气中心完全重合等，试验值也含有一部分不确定量。实际应用表明，桥路电阻只要在最佳值附近即可满足应用要求，理论计算和仿真分析结果可以作为最佳匹配电阻的有效估算值。

表2　三种方法结果对比Table 2 Comparison results of three methods

3　桥路信号调理和A/D转换

3.1信号调理

在最佳匹配电阻情况下，尽管桥路的灵敏度和信噪比很高，但这一信号仍是微弱的量，无法直接进行A/D采集，需要经过交流放大、滤波和相敏解调后再进行A/D采集。控制器在信号采集周期内（约）完成对每一路信号进行多次采样求平均，分别要对15个桥路依次操作，因此对调理电路的转化速度，转换质量有很高的要求［5］。经多方案对比研究，采用相敏解调器AD698，具体原理电路如图5所示，解调后输出电压与位置量关系曲线如图6所示。

依据陀螺浮子在壳体中的位置，将控制器工作范围划分为3个区段:1）浮子远离中心位置5μm；2）浮子距离中心位置在0.27μm（控制精度）与5μm之间；3）浮子已进入控制精度范围［3，5-7］。

控制方式描述如下:

图5　解调器电路原理图Fig.5 The principle diagram of demodulation circuit

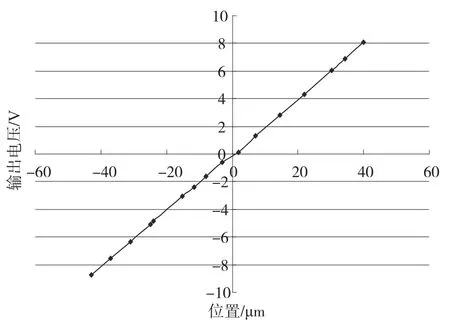
图6　解调后输出电压与位置量关系曲线Fig.6 The result between output voltage with demodulation and location signal

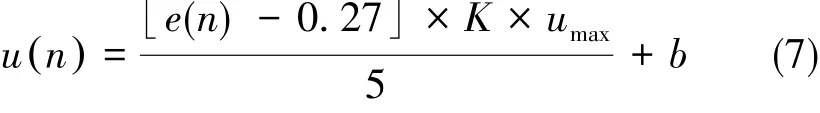
式中，e（n）为浮子位置偏差；b为磁悬浮拉动浮子所需的最小力；K为输出电压信号随位置信号的增益，依据调试情况确定。

在定中精度测试时，磁悬浮进入控制精度以后，根据调理电路输出的误差信号与标定系数的比值即为定中精度，测试结果如表3所示。

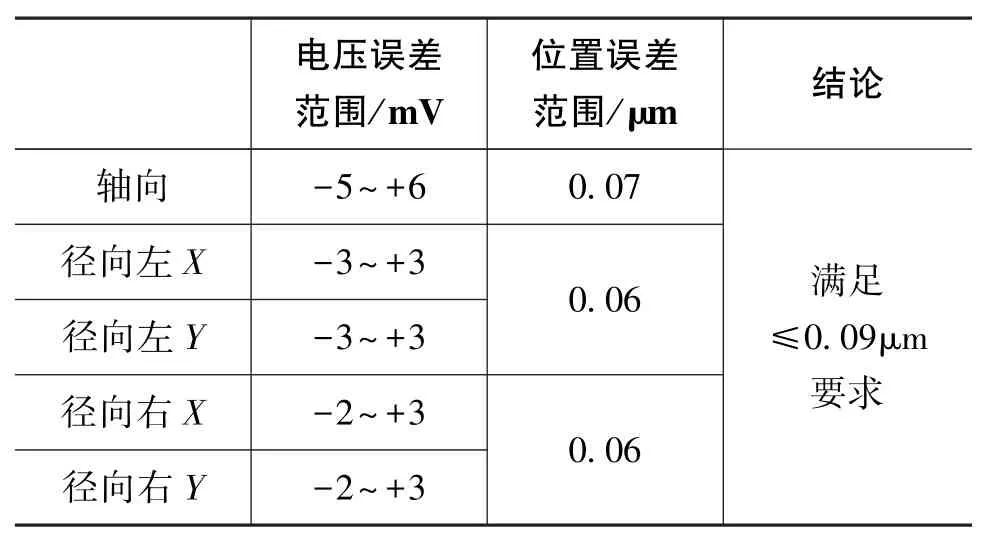
表3　定中精度测试结果Table 3 The test results of precision

3.2A/D转换

调理后的信号经A/D转换后进入SOC模块，A/D输入电压的量程为±10V，调理后的位置信号范围在0V～8V，满足量程。按照电路设计0.09μm控制精度计算，由于陀螺浮子最大变化范围为10μm，因此要求电路检测精度需高于以上控制精度。利用式（8）可以计算出A/D输入模块的精度位数。

式中，n为A/D输入模块的位数，n为整数。

因此，可求出n＞11。考虑到现有A/D输入模块位数，n可取12或16以上位数。在留裕度的情况下反推A/D精度，将输入满量程值带入计算。

计算可得εV=2.4mV，结合表3中的调理误差，最大误差电压为 8.4mV，位置精度为0.087μm，满足≤0.27μm要求。由于扩大了A/D的实际输入范围，因此电路实现的定中精度将优于0.09μm。

4　结论

准确地检测出陀螺浮子的位置是有源磁悬浮系统关键技术难题之一，是保证定中精度的先决条件。位置检测包括初始的差分位置信号的获取、调理放大、A/D转换三大部分，按论文中的思路和方法进行分析设计，可以保证电路的设计指标。调理误差和A/D转换误差累加结果小于8.4mV，对应的位置测量精度为0.09μm，为磁悬浮系统整体定中精度ε≤0.27μm提供了保障［5］。

［1］ 房建成，孙津济，樊亚洪.磁悬浮惯性动量轮技术［M］.北京：国防工业出版社，2012. FANG Jian-cheng，SUN Jin-ji，FAN Ya-hong.Magnetically suspendedinertialmomentumwheeltechnology［M］. Beijing：National Defense Industry Press，2012.

［2］ 徐旸，张剀，赵雷.磁悬浮轴承—理论、设计及旋转机械应用［M］.北京：机械工业出版社，2012. XU Yang，ZHANG Kai，ZHAO Lei.Bearing：theory，design，and application to rotating machinery［M］.Beijing：China Machine Press，2012.

［3］ 申志刚.有源磁悬浮方案报告［Z］.航天十六所. SHEN Zhi-gang.Report of active magnetic bearing project design［Z］.The 16thChina Aerospace Science and Technology Corporation.

［4］ 韩剑辉，许镇琳，赵承利.陀螺仪有源磁悬浮控制系统的设计与实现［J］.天津大学学报，2008，41（8）：937-940. HAN Jian-hui，XU Zhen-lin，ZHAO Cheng-li.Design for control system of active magnetic suspension used in gyroscope［J］.Journal of Tianjin University，2008，41（8）：937-940.

［5］ 赵丙权，谷云彪，凌林本，韩建辉，陈英华.数字式有源磁悬浮技术［J］.中国惯性技术学报，2005，13（2）：66-69. ZHAO Bing-quan，GU Yun-biao，LING Lin-ben，HAN Jianhui，CHEN Ying-hua.Digital active magnetic suspension［J］. Journal of Chinese Inertial Technology，2005，13（2）：66-69.

［6］ 邓忠武.三浮陀螺仪磁悬浮系统设计研究［D］.哈尔滨工业大学，2003. DENGZhong-wu.Researchonthedesignofactive magnetic bearing system with three-floated gyroscope［D］. Harbin Industry University，2003.

［7］ 杨孟兴，吴辽，王卿，申志刚，张微.基于位置信号的三浮陀螺仪有源磁悬浮干扰力矩补偿方法［J］.中国惯性技术学报，2015，23（6）：812-817. YANG Meng-xing，WU Liao，WANG Qing，SHEN Zhigang，ZHANG Wei.Distur-torque compensation for active magnetic bearing of three-floated gyroscope based on position signal［J］.Journal of Chinese Inertial Technology，2015，23（6）：812-817.

Research on Active Magnetic Bearing Position Detecting Circuits with Three-floated Gyroscope

WU Liao1，YANG Meng-xing1，WANG Qing1，SHEN Zhi-gang1，MA Qian-li2
（1.The 16thInstitute，China Aerospace Science and Technology Corporation，Xi'an 710100；2.Shanghai Magnetic Bearing Traffic Developing Company，Shanghai 201204）

High precisionε≤0.27μm of active magnetic bearing（AMB）is requested in three-floated gyroscope （TFG），and that of position signal detecting circuits should be higher than it，which is devised 0.09μm.Three aspects measures can be done to ensure this goal，L-R circuit，recuperating module and A/D transforming module.Two methods of finding the best resistances are introduced，simulation and calculation with experiment.The relation precision between of orientation and parameter of position signal detecting circuits has been deduced in this paper.And，the index of circuits is realized，proving that is superior to 0.09μm by calculation and experiment.

three-floated gyroscope（TFG）；active magnetic bearing（AMB）；detecting position；precision

U666.1

A

1674-5558（2016）02-01077

10.3969/j.issn.1674-5558.2016.03.008

2015-02-13

国家自然科学基金（编号:61075030）

吴辽，男，硕士，研究方向为惯性仪表及设备、磁悬浮技术。