基于局部声速优化和信号修正的超声成像算法

杨策

（四川大学计算机学院，成都　610065）

基于局部声速优化和信号修正的超声成像算法

杨策

（四川大学计算机学院，成都610065）

0　引言

人体构成复杂，各种组织不尽相同，这就导致了超声波在人体中传播，不同组织具有不同的传播声速。如在骨骼中传播速度为3700m/s,肌肉中传播速度约为1580m/s,乳房中速度仅为1420m/s。而现有的超声系统上常采用1540m/s作为系统声速，声速的不匹配，会造成成像质量不佳，如形变、相位不准确、对比度下降等问题。

针对这一问题，现今已经提出了很多种声速优化的算法，如在文献[1]中Jochen F.Kriicker's2，J.Brian Fowlks'. Paul L.Carson'采用多组不同角度的超感兴趣区域图像进行图像配准以此得到该区域的最佳声速；Larry Mo,David Napolitano在文献[2]中将包络信号作为横向傅里叶算法的输入，通过统计频谱随声速改变产生较大变化部分的能量来作为衡量最优声速的标准；文献[3]对超声聚焦点附近的原始射频数据做横向傅里叶变换，对结果进行分析，得到目标范围内的最佳成像效果；文献[4]通过观察超声图像性质以侧向对比度作为切入点，来作为判断最优声速的依据。此类算法的目标区域通常为聚焦区域，优化后将目标区域的最优声速作为全局的声速用于成像，然而非聚焦区域的声速可能并不匹配于优化后的全局声速，从而导致图像质量在非聚焦区域成像效果不佳。

为了解决以上问题，本文对超声图像进行整体划分，除了最为重要的主目标区域外，将其余部分分层为其他目标区域。采用一种可行的声速优化算法，得到每个区域的最佳声速，以主目标区域声速作为全局声速用于聚焦，之后采用相位修正算法在接收聚焦时对其余目标区域的原始射频数据进行处理，使得在整体采用一个系统声速时，图像的各个部分都能得到较好的成像效果。

1　声速的意义

超声探头由许多小阵元构成，在发射超声波时，每个小阵元向目标介质发射同心圆波束，当多个阵元同时发射同心圆波束时，由于波之间的互相干扰，波束可能加强，可能被削弱。在超声成像中我们希望同心圆波束会在目标点聚集以获得最强的叠加能量。

图1　探头波束形成示意图

在图1中横向为探头方向，纵向为深度方向，可以看出因为阵元距聚焦点f距离不同，因此需要对每个阵元设定发射延迟时间t，使得所有的同心圆波束能聚集于目标点f。因此若系统声速与组织声速不匹配则波束无法聚焦，接收聚焦时亦然。公式（1）为延迟公式,其中t为当前阵元延迟的时间，c为设定的用于计算延迟的超声系统声速。

对于非均匀组织如图2，上层组织声速为C1，下层组织声速为C2，将聚焦点定于点f，忽略折射。当在f点处得到最佳成像效果时最优声速应为C3（C1＜C3＜C2），而上层组织其最优声速为C1，若只对聚焦区域进行优化，采用优化结果C3作为系统声速，则上层组织成像效果不佳。

2　算法介绍

2.1基于FFT的声速优化算法

在声速优化算法中选取目标区域是十分重要的，通常目标区域是包含聚焦点的区域，但过大的目标区域会使得数据特性被削弱。而且在多次实验中可知，较小的目标区域可以更好地保留聚焦带来的影响。本文将组织进行分层，除了主要关注的区域，设定划分多个其他区域，对每个区域进行声速优化，需要设定多个聚焦点，考虑到时实性，声速优化算法要尽可能的简单高效，故不考虑图像处理相关的优化算法，而采用在信号上进行处理的方法。

在文献[3]中，采用RF数据作为FFT的输入源，没有考虑直流分量带来的影响，文献[4]中FFT的输入为包络信号，但包络信号进行FFT后损失很多的幅值信息。故本文采用IQ信号作为FFT的输入。

图3为仿真生成的超声单点成像图，可以看到随着声速的变化成像效果也发生改变，且改变在横向上最为明显。从左至右声速分别为1440m/s,1540m/s, 1640m/s，聚焦深度3cm为图中亮点处，组织声速为1540m/s。可发现成像效果在1540m/s的声速下达到最佳效果。

图3　超声单点成像图

图4中上层三幅图从左至右分别为采用1440m/s, 1540m/s,1640m/s的声速进行聚焦时，聚焦点处包络线图谱，下层三幅图为采用上述声速聚焦时，聚焦点处IQ信号进行FFT转换后的结果。无论是哪种图谱在声速为1540m/s（1540m/s为组织声速，在此声速下成像效果最佳）时其都具有波峰更高，波谷更低的特点。

将图4下层三幅图谱放到同一坐标轴中显示，如图5，可以看到在某个范围内频谱随着声速的改变有着较为明显的变化，根据文献[2]中提到的方法，我们可以通过预设标量来标记变化明显的范围，统计随声速改变变化明显的频谱幅值和来作为衡量聚焦效果的质量因子。

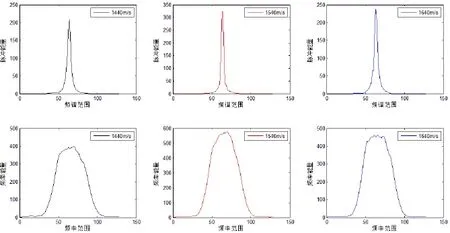
图4　聚焦点处包络信号及IQ信号FFT结果

图5　FFT结果图

通过以上分析可得到本文改进后的声速优化算法，算法流程如下：

●采用原始未经过任何处理的RF数据，对其进行正交解调，得到对应的IQ数据。

●选择包含聚焦点的区域为目标区域，在目标区域深度内横向选择多行IQ数据，进行横向傅里叶变换。

●将得到的多条FFT频谱做平均，得到最后的频谱。

●在多个声速下重复以上过程，观察所有频谱，确定频谱随声速变动改变较大的范围。

●将设定范围内的频谱能量求和，找出频谱能量最大时对应的声速，作为最优声速，用于最终成像。

2.2相位修正算法

通过对目标组织进行多区域划分，对每个区域设置聚焦点，进行声速优化，可得到该区域的最佳成像声速，但在超声系统成像中，只能设定一个声速作为系统声速，故除主要目标区域外的其他区域得不到最佳成像效果，这就需要以该区域的最优声速对其进行相位修正。以使得同一位置的数据具有相同的相位，不正确的声速则会在此步骤时产生偏差。故在声速不匹配情况下相位修正公式（2）如下：

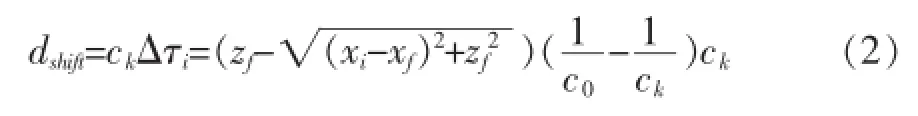
其中Zf为聚焦点Z轴坐标，Xf为聚焦点X坐标，Xi为接收点X坐标，C0为系统声速，CK为优化后的最佳声速，dshift为在经过系统声速进行接收聚焦相位平移后，目标区域需要进行的相位修正的量。

综上所述可以可到本文算法的总体流程：

图6　算法流程图

3　实验结果

为验证本文提出的算法，目标组织需为不均匀组织且有已知确定声速，而相位修正算法需要在接受聚焦之前对数据进行相位修正，而现有超声系统数据都已封装，故采用计算机仿真的方式来进行实验。在仿真中我们用到的模拟组织的数据结构是一个20mm× 60mm的区域，这个区域被分成1200个小格子（格子大小为1mm×1mm），每个小格随机分布49个散射点，共59800个散射点。

3.1均匀组织声速优化

图7　均匀组织斑点成像

此处为斑点图像的仿真，设定真实声速为1540m/ s。图7从左至右是系统声速分别为1540m/s，1640m/s，聚焦深度在3cm时的成像。由图可以看出在系统声速为1540m/s（图7左边图片）时，具有更好的成像效果。对聚焦点位于该深度的一组不同声速 （1440m/s-1640m/s）生成的超声图像划定目标区域进行声速优化，采用本文提及的算法，优化结果图8，可以看出，本文提出的算法能够准确地计算出最优声速。

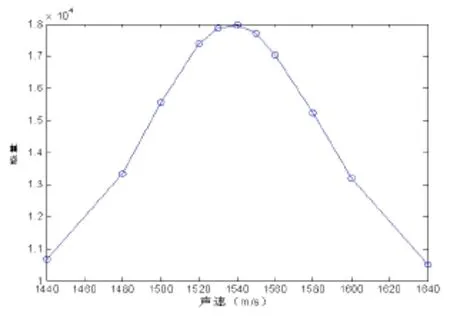
图8　斑点成像声速优化结果

3.2分层组织声速优化

此实验为分层声速仿真（忽略折射），将目标组织分为三层，三层组织真实声速由上到下分别为1430m/s，1500m/s，1540m/s，每层高度都为2cm。分别在1.2cm, 3.3cm，4.5cm处设定一亮靶点。图9为聚焦点在4.5cm处的不同系统声速下的成像。由图像可以看出三个亮点分别在声速为1430m/s,1460m/s,1480m/s时达到最佳成像效果。图10由上到下分别为对包含1.3cm，3.3cm，4.5cm处亮点的区域进行声速优化的结果，分别在1430m/，1460m/s，1480m/s处取得最大值。

图9　分层组织成像图

3.3相位修正

将第三层4.5cm点处作为主目标区域，传统优化算法使用其最优声速1480m/s进行成像得到图（a），而通过本文算法对其余区域进行相位修正后，采用1480m/s作为系统声速时成像如图（b），可以看到第一个亮靶点与第二个亮靶点在横向上的扩散程度较修正之前有了一定提高。

图10　分层组织声速优化结果

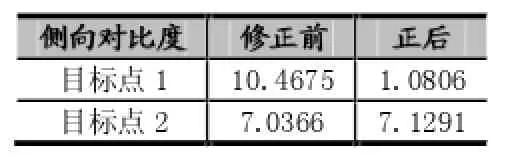
表1　侧向对比度比较表

在目标点周围选取相同大小的区域做侧向对比度的计算，计算方法来自文献[4]。结果如表1，可以看出修正后的侧向对比度高于修正前。而由于本来修正前后声速差距不大，且主要对亮靶点进行分析，故也并不会有大范围的提升。

图11　结果比较图

4　结语

通过计算机仿真的实验结果可以看出，本文提出的算法相较于传统声速优化算法来说，在成像效果上有了提高。但本文目标区域选取范围较小，在优化中对多个划分的局部区域需选取多个聚焦点，过程略为繁琐，后期可结合图像处理的方法对图像进行预处理划分组织类似区域，框定优化范围，减少算法运算量，提高优化准确性，将此方法运用于实际中。

[1]Jochen F.Kriicker's,J.Brian Fowlks'.Sound Speed Estimation Using Ultrasound Image Registration[J]．IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,vol.51,no.9,september 2004.

[2]David Napolitano*,Ching-Hua Chou,Glen McLaughlin,Ting-Lan Ji,Larry Mo,Derek DeBusschere,Robert Steins．Sound Speed Correction in Ultrasound Imaging[J]．Ultrasonics 44（2006）.

[3]Huanhuan He and Dong C.Liu．Sound Speed Optimization Based on Acoustic Point Spread Function[J]．IEEE，2009.

[4]李晓瑛,刘东权．基于图像对比度分析的自适应超声声速优化[J]．生物医学工程学杂志,2011.

[5]杜恒．超声系统声速优化模拟与算法[J].中国生物医学工程进展，2007.

[6]夏春兰，石丹，刘东权.基于CUDA的超声B模式成像[J].计算机应用研究，2007.

Ultrasound Imaging;Local Sound Speed Optimization;Phase Correction

Ultrasound Imaging Algorithm Based on Local Sound Speed Optimization and Signal Correction

YANG Ce
（College of Computer Science,Sichuan University,Chengdu 610065）

1007-1423（2016）03-0072-06

10.3969/j.issn.1007-1423.2016.03.017

杨策（1991-），女，贵州六盘水人，在读硕士研究生，研究方向为超声系统声速优化相关算法

2015-12-01

2015-12-30

在超声成像中与组织声速匹配的系统声速会带来最佳的成像效果，因此，多种超声声速优化算法已经提出。传统优化方法选定包含聚焦点的区域作为感兴趣区域，优化后将得到的最佳声速作为系统声速用于成像，这会导致非聚焦区域组织声速不匹配，导致局部成像效果不佳。对现有声速优化算法进行改进，再结合所提出的相位修正算法，解决局部成像效果不佳的这个问题，在整体上提高超声图像质量。通过计算机仿真的方式进行实验，结果表明经该算法修正后的超声图像，图像质量有所提高。

超声成像；局部声速化；相位修正

In ultrasound imaging system,if the assumed sound speed match the true sound speed propagated in the tissue,then the system can bring better imaging quality.Therefore,many kinds of ultrasonic speed optimization algorithms have been proposed.The traditional optimization method selected the region which contains the focusing region as the region of interest,after that the best sound speed will be used as the system sound speed for imaging.It will lead to the other region mismatch the system sound speed,resulting in poor local imaging.Improves the sound speed optimization algorithm,and proposes the phase correction algorithm.With these two algorithms,the problem that local regions have the poor imaging quality can be solved,and the overall image quality can be improved.Through the computer simulation,testing results show clear improvement in ultrasound image quality.