异构信息网络概率模型研究及社区发现算法

殷浩潇，李川

（四川大学计算机学院，成都　610065）

异构信息网络概率模型研究及社区发现算法

殷浩潇，李川

（四川大学计算机学院，成都610065）

国家自然科学基金（No.61103043）；国家“十二五”科技支撑计划项目（No.2012BAG04B02）

0　引言

信息网络将现实中复杂系统的实体抽象为网络中的节点，并把实体之间的联系抽象为网络图中的边，用以刻画网络系统中有价值的性质和潜在的规律。进一步地，若信息网络中包含了多种类型的节点和不同类型的边，则称为异构信息网络，它能够蕴含更加丰富的信息，更加逼近现实世界系统。挖掘其中的社区结构，有助于进行社会网络分析、研究群体行为和社区效应，具有重要的理论意义与应用价值。例如，在基于兴趣划分的社区中，根据目标产品的特点，针对可能感兴趣的社区网络中的客户进行定向广告投放，推荐一系列相关的产品，从而提高点击转化率，提高交易成功率[1]；对科研合作网络进行社区发现，可以发现合作关系紧密的学者及其研究兴趣的变化趋势等。

常见的社区发现算法或社会网络聚类算法多是基于同构网络[2]或特定类型的网络[3-6]，并且多是通过分析拓扑结构来进行[2]。然而，通过网络拓扑结构很难全面地发现网络中潜在的社区结构，其原因有：（1）局限性，通过拓扑结构的方法多是基于同构网络，而现实中多是复杂的异构网络，难以实用；（2）不能充分利用异构网络中多种类型节点和边所蕴含的丰富信息。

针对以上问题，本文提出了基于异构信息网络信息维统计量的社区发现方法（Dir-Com），首先通过引入模块度最大化曲线的层次化狄利克雷过程自适应地学习社区数目,然后通过对异构信息网络进行信息维上卷，用上卷后信息维的概率分布来表征某个社区，再通过计算后验概率进行社区发现。

1　异构信息网络信息维上卷

一个异构信息网络G是包含了多种类型的节点和多种类型的边的网络。不同于传统的社区发现方法只局限于同构网络，本文针对异构信息网络进行社区划分，结果是生成一个异构的子图。本文中将某个对象在某个社区中的分布频数定义为与该对象信息维度在该聚类中的分布频数。例如若某个作者在数据挖掘领域发表了4篇论文，则该作者在数据挖掘领域中的分布频数就是4。对于如何计算某个对象的分布频数，本文采用信息维上卷的方法。

定义1（信息维）设待分析图结构为G（V，E）=G（V，θ（ID））。其中，V是图中点的集合，E表示边的集合，函数θ为图G的边信息决定函数。设变量ID={I1，I2，…，Im}是目标节点待考察的维度集合。这m个信息属性构成的维度集合只能决定图的边集，不能改变图的拓扑结构，称ID为信息维。

信息维上卷则是将相同类型的节点与目标对象连接的边权值进行累加。上卷过后就得到某个节点Ai在各个社区C={C1，C2…}中的分布频数的向量。

根据贝叶斯统计理论，假设节点在不同社区的频数概率分布服从一个先验分布，即待估的参数，每得到一次新的观测结果，则会更新分布参数，从而进行修正来拟合潜在的分布。本文采用狄利克雷分布来表示信息维的分布。

2　概率模型

狄利克雷分布是一组连续多变量概率分布，是多变量普遍化的Beta分布，其概率分布如下：

狄利克雷分布常作为贝叶斯非参数估计中多项分布的先验概率[10]。

多元变量的情况，考虑到对于多项分布的似然函数为：

则根据贝叶斯参数估计理论，选择狄利克雷分布作为多项分布共轭先验分布。那么估计参数μ时，我们用p（μ）表示概率分布函数，用p（μ|D）表示观测值D的似然函数。根据后验=似然*先验，有：

从这个形式可以看出，后验也是狄利克雷分布。把这个后验归一化后得到:

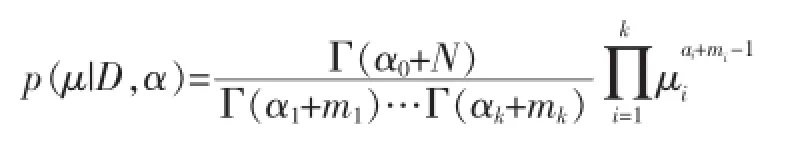
3　异构网络中的社区发现

假设在度量空间上的分布G0和一个参数α，如果对于度量空间的任意一个可数划分（有限或无限），都有下列式子成立：

我们说，G满足参数为G0和α的狄利克雷过程，即：G～DP（α，G0）。

进一步地，层次狄利克雷过程定义如下：

基础分布G0的离散性保证了多个随机测度之间共享原子[15]，从而很好地适应了社区发现中的社区重叠和覆盖的问题。

如何根据数据分布来自适应地确定社区的数目K是社区发现或聚类的关键问题。常用的确定K的方法有：（1）根据经验人工设定[1]，该方法不适用于规模大或动态网络；（2）交叉验证法，通过设置不同的K值训练后验证比较求得最佳值，该方法时间复杂度较高。

Blei等人[14]提出过一个方法，采用设置不同的K数值，画出K-perplexity曲线，然后找到曲线中的纵轴最高点便是K数量的最佳值。受到该方法启发，本文采用层次狄利克雷过程模型进行多次迭代后统计出现次数最多的多个K值，再画出K-log（modularity）曲线，然后通过求导求得极值点作为最佳的K值。

其中采用狄利克雷过程计算K值的算法如下：算法1自适应聚类数目确定算法

输入：信息维进行上卷后的异构信息网络G（V，θ（ID）），阈值γ

输出：社区数目K

针对异构信息网络中的社区发现问题本文提出了Dir-Com算法，该模型基于狄利克雷分布，构建模型的过程就是进行估计参数的过程。若假设某个目标节点的每个属性维度j都有一个概率pjk在社区Ck中生成，则该概率分布就是一个多项分布，根据贝叶斯理论，选取狄利克雷分布作为属性维度在不同社区的先验概率分布，即多项分布的共轭先验分布。那么，节点i属于社区k的概率为：

根据以上公式计算节点i属于某个社区的最大后验概率，然后将其归入某一社区，同时根据社区中信息维的分布情况，更新分布参数。

4　算法描述

基于狄利克雷过程的异构信息网络社区发现算法如下：

步骤 1：采用层次狄利克雷过程，设置迭代次数> 1500，取1000次之后的结果，得到出现次数最多的多个K值，计算出K-log（modularity）曲线，然后找到曲线中的纵轴最高点便是K数量的最佳值。

步骤2：根据上一步计算得出的最佳社区数目K，对信息网络中的异构节点集合A做可数划分（A1，A2，…，Ak），对于所有划分Ai，根据狄利克雷分布，通过训练数据迭代计算其分布参数。

步骤3：对于测试数据，根据最大后验概率来确定其属于哪个划分（社区），并返回步骤2更新分布参数。

5　实验及结果分析

空手道俱乐部网络数据是用于社区挖掘算法的常用数据集之一，这里选用同构信息网络目的在于验证本文算法对于同构网络同样具有很好的社区发现效果。百度贴吧数据集则包含了百度微信贴吧用户的属性及兴趣标签数据。数据集的具体信息如表1。

表1　数据集信息

对比算法：基于Jaccard距离的Kmeans算法。对比标准：模块度（Modularity），其定义为[17]：

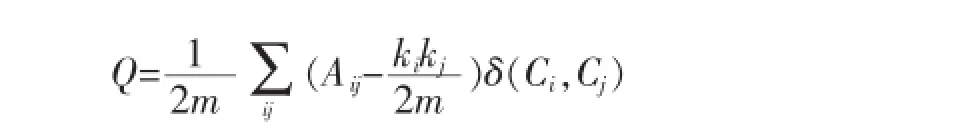
模块度可以用来衡量社团发现结果的好坏，在给定网络的情况下，模块度越大，说明社团发现的结果越合理。

如图1（a）所示，可以观测到在百度数据中，约2000次迭代之后K的值在一个稳定的区间里浮动。这里选择2000次迭代之后出现次数多的5个的K值作为候选集，画出K-log（modularity）曲线如图1（b）所示，求出曲线极值点作为社区的数目K。

图1　百度贴吧数据实验结果

如图2 所示，对比基于Jaccard相似性的K-means算法，本文算法得到的结果具有更好的模块度和稳定性，而K-means算法的结果尽管很少几个结果模块度较高，但其他结果的模块度非常不理想，甚至有很多负值。分析其原因，多是由于K-means算法选择需要初始随机种子点，不同的随机种子点会得到完全不同的结果，从而导致聚类结果不稳定。本文算法由于采用层次狄利克雷过程，通过多次迭代构建目标节点信息维与社区之间的概率分布模型，并根据贝叶斯参数估计理论进行参数学习，最大程度地拟合潜在的真实社区分布情况，从而获得更好的社区发现效果。

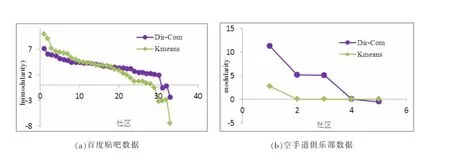
图2　社区发现效果对比

6　结语

本文提出了基于异构信息网络信息维统计量的社区发现算法（Dir-Com），该算法对异构信息网络进行信息维上卷后，学习信息维的狄利克雷分布参数来表征某个社区，再利用最大后验概率来计算社区发现，在自适应地确定社区数目这个问题上，本文采用了引入K-log（modularity）曲线的狄利克雷过程，并通过实验验证了算法的有效性和稳定性。

[1]唐磊.社会计算：社区发现和社会媒体挖掘[M]．北京：机械工业出版社，2012.

[2]张永辉，李川，唐常杰，等.基于结构分析的信息网络社区趋势预测[J].计算机科学与探索，2015（4）:403-409.

[3]C Li，WK Cheung，etc.The Author-Topic-Community Model for Author Interest Profiling and Community Discovery[J].Knowledge& Information Systems，2014，44:1-25.

[4]M Sachan，D Contractor，etc.Probabilistic Model for Discovering Topic Based Communities in Social Networks[C].ACM International Conference on Information&Knowledge Management，2011:2349-2352.

[5]Y Sun，Y Yu，etc.Ranking-Based Clustering of Heterogeneous Information Networks with Star Network Schema[C].In KDD'04，2009: 797-806.

[6]D Zhou，E Manavoglu，etc.Probabilistic Models for Discovering E-communities[C].International Conference on World Wide Web，2006:173-182.

[7]刘军.社会网络分析导论[M].北京：社会科学文献出版社，2004.

[8]李航.统计学习方法[M].北京：清华大学出版社，2012.

[9]C.Bishop.Pattern Recognition and Machine Learning[M].Springer，2007.

[10]Dirichlet Distribution.http://en.wikipedia.org/wiki/dirichletdistribution.

[11]D.Blei，A.Ng，etc.Latent Dirichlet Allocation[J].JMLR，2003:993-1022.

[12]D Koller，N Friedman.Probabilistic Graphical Models:Principles and Techniques[M].MIT Press，2009，42（2）:161-168.

[13]G Heinrich.Parameter Estimation for Text Analysis[J].Technical Report，2004.

[14]Li X，Bilmes J.A Bayesian Divergence Prior for Classifier Adaptation[J].J Mach Learn Res，2007，2:275-282.

[15]梅素玉，王飞，周水庚.狄利克雷过程混合模型、扩展模型及应用[J].科学通报，2012，57（34）:3243-3257.

[16]Teh Y，Jordan M，etc.Hierarchical Dirichlet Processes[J].J Am Stat Assoc，2005，101:1566-1582.

[17]Newman M E J，Girvan M.Finding and Evaluating Community Structure in Networks[J].Physical Review E，2004，69（2）:026113.

Heterogeneous Information Network;Community Discovery;Dirichlet Distribution

Research on Probabilistic Model of Heterogeneous Information Network and Community Discovery Algorithm

YIN Hao-xiao，LI Chuan
（College of Computer Science，Sichuan University，Chengdu 610065）

殷浩潇（1989-），男，四川泸州人，硕士研究生，研究方向为数据挖掘、信息网络

2015-12-22

2016-01-30

传统的社区发现方法多是基于同构网络和拓扑结构，为此，提出基于异构信息网络信息维统计量的社区发现算法，该算法通过对异构信息网络进行信息维上卷后构建概率模型，采用引入模块度最大化曲线的层次化狄利克雷过程自适应地确定社区数目，然后通过狄利克雷分布来表征某个社区，再通过计算最大后验概率来进行社区发现。实验表明，所提出算法相比基于拓扑结构的算法具有更好的社区发现效果和稳定性。

异构信息网络；社区发现；狄利克雷分布

李川（1977-），男，河南郑州人，博士，副教授，硕士生导师，研究方向为数据库、数据挖掘

As traditional community discovery methods are based on the homogeneous network and topology structure,presents a community discovery algorithm based on information dimension statistics of heterogeneous information network.This algorithm rolls up information dimension to build probabilistic model,uses hierarchical Dirichlet process with modularity maximization curve to adaptively determine the number of communities,characterizes communities with Dirichlet distribution and discovers communities by calculating the maximum posterior probability.Experiments show that compared with the algorithm based on topological structure,the proposed algorithm has better community discovery effect and stability.