一种基于广义旁瓣相消的稳健降维方法

孔永飞，吴海洲

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)



一种基于广义旁瓣相消的稳健降维方法

孔永飞，吴海洲

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

在自适应阵列信号处理中，为了高效进行干扰和噪声对消，提出了一种基于广义旁瓣相消的稳健降维方法。该方法利用信号子空间特征矢量和期望信号的投影导向矢量构造稳健降维阻塞矩阵，阻塞期望信号和噪声分量，使辅助支路中只含有干扰信号，达到了降维的效果，同时提高了算法对阵列天线误差的稳健性。仿真结果表明，该方法对阵列模型误差不敏感，可以有效地降低运算时间。

GSC；降维；阻塞矩阵；稳健性

0　引言

自适应阵列处理技术已广泛地应用于雷达[1]、声纳、通信、声学、地震学和医学等众多领域。在实际应用中，为了获得更好的性能，阵列中的阵元数可能成千上万，如果采用全阵自适应波束形成，系统的运算量过大，为了减少信号处理中的运算量和复杂度，加快自适应算法的收敛速度，通常需要采用降维处理。

文献[2]根据选定约束条件的个数，控制自由度进而实现降维，需要已知约束方向的先验知识。文献[3]提出功率空间的思想，借助最小二乘和奇异值分解，构造阻塞降维矩阵，增加运算量。

本文利用信号特征子空间构建降维阻塞矩阵，应用于广义旁瓣相消器(GSC)，降低了自适应的维数。

1　GSC

GSC是线性约束最小方差(LCMV)的一种等效实现结构[4]，框架如图1所示。

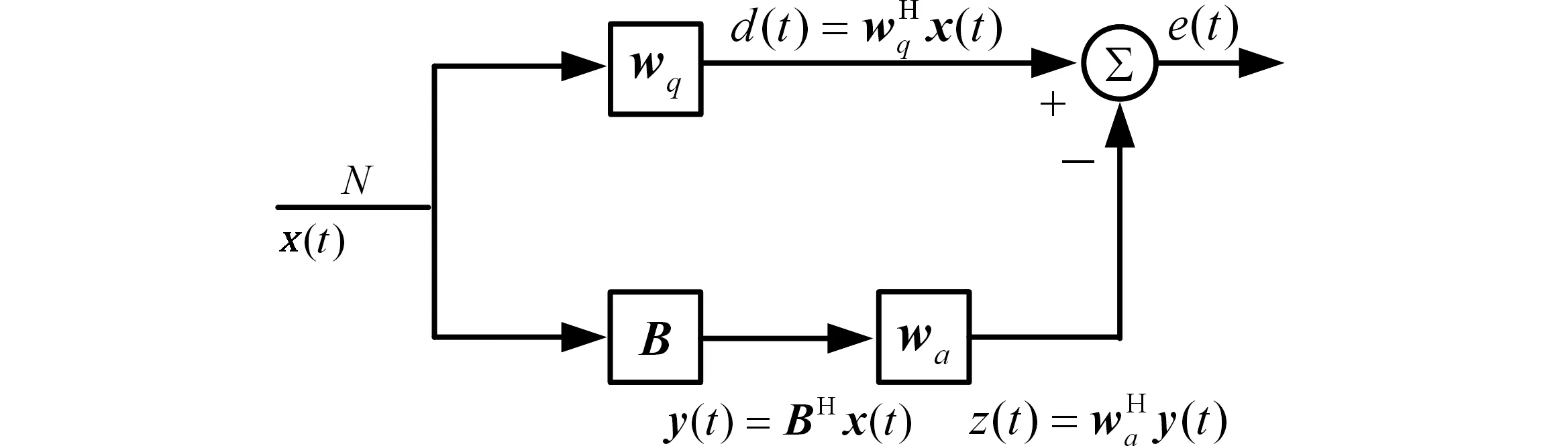
图1　GSC结构

GSC结构将自适应波束形成的约束优化问题转换为无约束的优化问题，分为自适应和非自适应2个支路，其中上支路变换后得到参考信号d(t)，d(t)含期望信号、干扰和噪声分量，而下支路通过阻塞矩阵B，阻塞掉期望信号，则y(t)只含干扰和噪声分量。显然上、下支路中的干扰信号是相关的，变换后的信号进行维纳滤波，则干扰可自适应抵消，上支路中的期望信号被无失真输出。权向量w被分解成静态权wq和自适应权wa两部分，可表示为

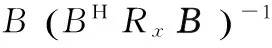
(1)

式中，B为阻塞矩阵；Rx为信号协方差矩阵。图1中，

d(t)=wHqx(t)，

(2)

y(t)=BHx(t)。

(3)

式中，x(t)为阵列接收信号。根据维纳滤波原理，自适应权向量wa可表示为：

wa=R-1yryd，

(4)

Ry=BHRxB，

(5)

ryd=BHRxwq。

(6)

Ry是y(t)的协方差矩阵；ryd是y(t)与d(t)的互相关矢量。

由于阵列天线误差[5]的存在，影响了自适应波束形成的性能[6]，GSC的阻塞矩阵并不能很好地将期望信号阻塞，而使其一部分能量泄露到辅助支路中，当信噪比比较高时，辅助支路也含有相当地期望信号能量，引起期望信号相消，导致输出信干噪比下降。

2　构造稳健降维阻塞矩阵的新方法

GSC并不能抑制白噪声，其输出信干噪比的提高是靠抑制干扰信号分量，辅助通道中只需包含干扰分量即可，即利用稳健降维阻塞矩阵B(维数为N×(M-1)，N为阵元个数，M为目标信号与干扰信号之和)阻塞噪声和期望信号，只允许干扰信号通过，有效提高输出信号的信干噪比。

阻塞矩阵B的作用有两方面:一方面阻塞进入辅助支路中的期望信号和噪声分量；另一方面实现降维处理。

文献[7]提出利用正交补空间理论构造降维阻塞矩阵，本文基于子空间理论，提出一种线性组合原理构造降维阻塞矩阵B的算法，与前者相比，无需计算正交补空间的投影矩阵，有效地降低了运算量。

对阵列协方差矩阵Rx进行特征分解：

(7)

设特征值λ0>λ1>…>λM-1>λM=…=λN-1，v0,v1,…,vN-1为相应特征值对应的特征向量，可根据ADL准则[8]、MDL准则[9]和盖尔圆准则[10]估计获得信源个数。将信号向量矩阵记为Us，噪声向量矩阵记为UN，则

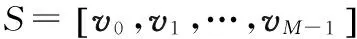
(8)

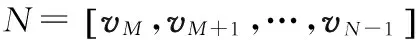
(9)

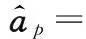
(10)

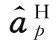
(11)

即可满足B与C正交。

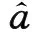
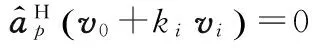
(12)

式中，ki为线性组合系数，得到

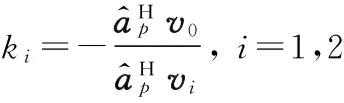
(13)

利用以上得到的线性组合系数ki，构造降维阻塞矩阵如下：

(14)

式中，

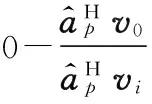
(15)

满足BHC=0，达到阻塞噪声和期望信号的目的。把降维阻塞矩阵B应用于式(1)，得到自适应权矢量w。

与文献[7]相比，由于原理一致，2种算法都满足BHC=0，得到的自适应权向量一致。但文献[7]中，需计算C的正交补空间，即

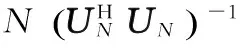
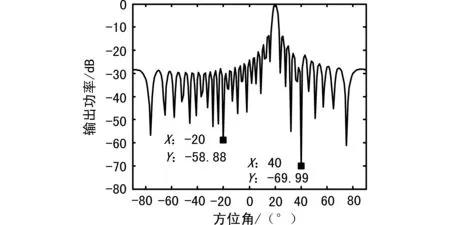
在大型阵列应用中，阵元数N较大，目标与干扰个数之和为M，满足M<

3　仿真验证

以阵元数N=32的半波长均匀线阵为例，假定来自不同方向的远场窄带信号互不相关，信号与加性噪声也不相关。假定期望信号来自20°方位，信噪比为0 dB，2个干扰信号分别来自40°和-20°，干噪比分别为30 dB和20 dB。

3.1自适应波束方向图

所提算法的自适应波束方向图如图2所示，在干扰方向40°和-20°形成零陷，在40°方向零陷深度达到-69.99 dB，在-20°方向零陷深度达到-58.88 dB，能有效消除干扰。

图2　自适应波束方向图

3.2构造降维阻塞矩阵的时间对比

表1列出了2种构造降维阻塞矩阵算法在Matlab中的运算时间，通过100次Monte Carlo试验得到的平均时间，以s为单位，t1为本文算法运行时间，t2为文献[7]中算法运行时间，随着阵元数的增大，t1增长较少，t2增长明显，2种算法的时间差距越来越大，本文所提算法有效地降低了运算时间。

表1　运行时间比较

3.3输出信干噪比

快拍数从50递增到500，通过300次Monte Carlo试验的平均得到图3的曲线。

图3　输出信干噪比随快拍数变化的曲线

如图3所示，所提算法的信干噪比变化曲线接近于理论值，与文献[7]中算法的干噪比变化曲线一致，明显优于传统的GSC，这是因为估计的协方差矩阵与实际的协方差矩阵存在误差，通过传统方法构造得到的，并不能很好地阻塞期望信号，辅助通道中会有一定的泄露。

所提方法通过线性组合算法构造降维阻塞矩阵，有效消除下支路信号和噪声分量，提高上下支路中干扰信号的相关性，有更好的干扰对消性能，并对静态导向矢量向信号子空间做投影处理，进一步减少期望信号的泄露。

3.4指向偏差的稳健性

指向偏差为5°时的波束方向图如图4所示，在干扰方向40°和-20°形成零陷，在40°方向零陷深度达到-69.99 dB，在-20°方向零陷深度达到-59.23 dB，能有效消除干扰，同时在期望信号方向20°形成主波束，避免了期望信号相消现象，提高了阵列在存在指向偏差时的稳健性。

图4　指向偏差为5°的方向图

指向偏差从0°增加到5°，快拍数为500，通过300次Monte Carlo试验平均得到如图5所示的曲线。

图5　输出信干噪比随指向偏差变化的曲线

如图5所示，所提算法与文献[7]中算法一致，对指向偏差保持有良好的稳健性。指向偏差从0°增加到5°，所提算法的性能曲线与理论值相差较小，而传统GSC方法随着指向偏差的增大，其输出信干噪比几乎成指数衰减。

4　结束语

本文提出构造降维阻塞矩阵的新方法，利用线性组合原理，降低了构造阻塞降维矩阵的运算量，在抑制干扰的同时大大减少了GSC自适应权的维数，降低了系统的运算量，提高了算法的稳健性，仿真试验及性能分析都验证了算法的有效性和优越性。

[1]王永良.自适应阵列处理[M].北京：清华大学出版社，2009.

[2]MA T T,GRIFFITHS L J.A Solution Space Appr oach to Achieving Partially Adaptive Arrays[C]∥Proc Int Conf Acoust,Speech,Signal Processing,New York,1988:2 869-2 872.

[3]BUCKLEY K M,GRIFFTHS L J.An Adaptive Generalized Sidelobe Canceller with Derivative Constraints[J].IEEE Trans on AP,1986,34(3):311-319.

[4]JABLON N K.Adaptive Approach to Linearly Constrained Adaptive Beamforming[J].IEEE Trans on AP,1986,34(8):996-1 012.

[5]见伟，张玉，韩名权.阵列天线通道误差对波束性能的影响分析[J].无线电工程，2014，44(11)：45-48.

[6]邓志鑫.阵列误差对Capon波束形成算法的影响分析[J].无线电通信技术，2012，38(2)：41-43.

[7]张涛麟，廖桂生，曾操.基于广义旁瓣相消的新降维方法[J].雷达科学与技术，2007，5(3)：213-219.

[8]WAX M,FUBRMANN D R.Detection of Signals by Information Theoretic Criteria[J].IEEE Trans on ASSP,1985,33(4):387-392.

[9]张杰，廖桂生，王珏.对角加载对信号源数检测性能的改善[J].电子学报，2004，32(12)：2 094-2 097.

[10]贡彦飞.基于盖尔圆准则的信源个数估计算法比较[J].无线电通信技术，2012，38(4)：57-59.

[11]郭庆华，廖桂生.一种稳健的自适应波束形成器[J].电子与信息学报，2004，26(1):146-150.

孔永飞 男，(1987—)，硕士，工程师。主要研究方向：航天测控、阵列信号处理。

吴海洲 男，(1977—)，博士，高级工程师。主要研究方向：航天测控、阵列信号处理。

A Robust Dimension Reduction Method Based on GSC

KONG Yong-fei,WU Hai-zhou

(The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China)

In adaptive array signal processing,a robust reduced-rank adaptive beamforming algorithm is proposed in this paper to get a better performance of interference cancellation and noise cancellation.A robust block and dimension reduction matrix using the structure of eigen-subspace is proposed to block the desired signal and noise.Therefore,not only can interferences be suppressed,but satisfactory dimension reduction be acquired also.By using robust processing,the proposed algorithm is not sensitive to the system error.Simulation results show that the proposed algorithm is not sensitive to the system error and it can reduce computation time effectively.

GSC;dimension reduction;block matrix;robustness

10.3969/j.issn.1003-3106.2016.09.10

2016-05-10

TTN911

A

1003-3106(2016)09-0041-04

引用格式：孔永飞,吴海洲.一种基于广义旁瓣相消的稳健降维方法[J].无线电工程,2016,46(9):41-44.