带非线性阻尼项n维欧拉方程组经典解的爆破
2016-09-22朱旭生赵康鑫傅春燕
朱旭生,赵康鑫,傅春燕,王 莉
(华东交通大学 理学院,江西 南昌 330013)
带非线性阻尼项n维欧拉方程组经典解的爆破
朱旭生,赵康鑫,傅春燕,王莉
(华东交通大学 理学院,江西 南昌 330013)
研究了n维空间带非线性阻尼项的等熵欧拉方程组初值问题经典解的爆破。当初值条件有紧支集时,利用泛函方法,证明了如果非线性阻尼系数有界时,其初值问题的经典解必定会在有限时间内爆破。
非线性阻尼;欧拉方程组;泛函方法;经典解;爆破
0 引言
本文主要考虑如下n维等熵可压缩欧拉方程组的初值问题:
(1)
对应的初始条件为:
(2)
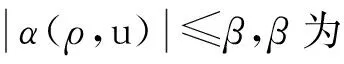
对于欧拉方程组经典解的研究有很多,主要集中在一维或三维空间中欧拉方程组整体解存在[1-4]以及经典解的爆破[5-11]方面。文献[1-3]分析了带线性阻尼项的等熵欧拉方程组,当初始数据是常状态附近的小扰动时,利用能量估计法,证明了经典解的整体存在。文献[5,7-8]研究了不带阻尼项的可压缩欧拉方程组经典解的爆破。而对于带非线性阻尼项的欧拉方程组的研究[4,6]却很少。本文在文献[6]的基础上,将一维空间中的阻尼系数(α+f(u))推广到n维空间的一般非线性函数α(ρ,u)。结合文献[5]的方法,分别在m(0)≥0和m(0)<0这两种条件下,通过构造适当的泛函,得到了当初始数据较大时,经典解不会整体存在的结论。
1 预备知识
定义
(3)
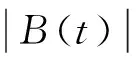
引理1[1]设(ρ,u)是初值问题(1)和初始条件(2)在Rn×[0,T)的C1解,则:
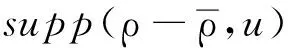
(4)
引理2[5]设(ρ,u)是初值问题(1)和初始条件(2)在Rn×[0,T)的C1解,则对所有的0≤t
m(t)=m(0)。
(5)
2 主要结论
定义:
F1(t)=∫Rnx·ρudx=∫B(t)x·ρudx;
(6)
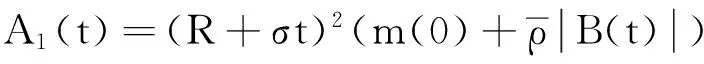
(7)
当m(0)≥0时,若F1(0)足够大,可以证明初值问题(1)和初始条件(2)的经典解会爆破。
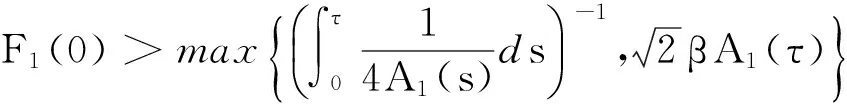
证明由于
F1(t)=∫Rnx·ρudx=∫B(t)x·ρudx,
所以
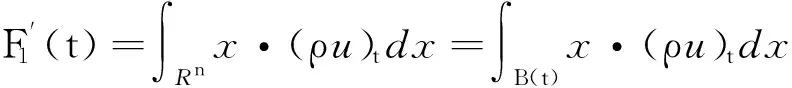
再由初值问题(1),通过分部积分得到:
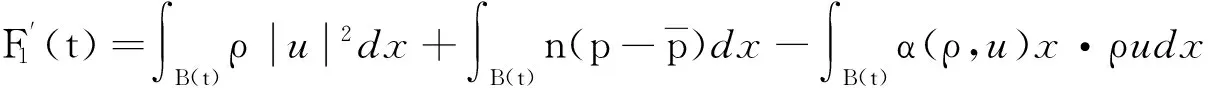
(8)
其中:
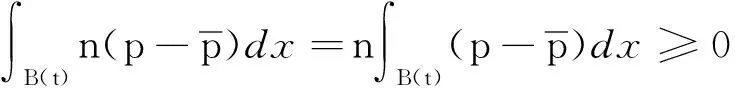
可以采用Hölder不等式进行证明:
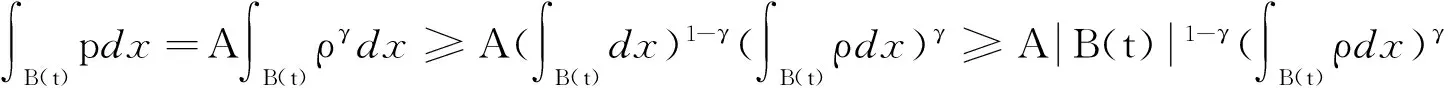
由于
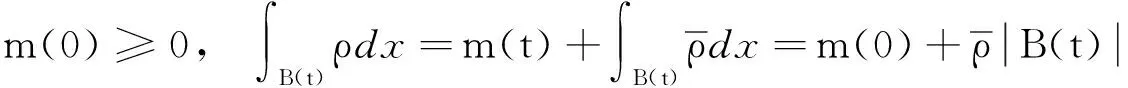
所以
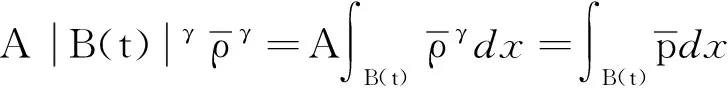
(9)
另外,对于∫B(t)α(ρ,u)x·ρudx的处理,有:
采用Schwarz不等式和基本不等式,对上式作以下处理:
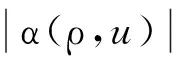
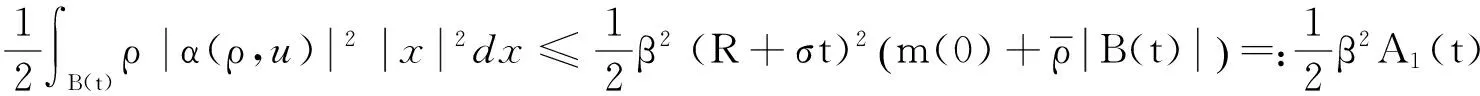
所以
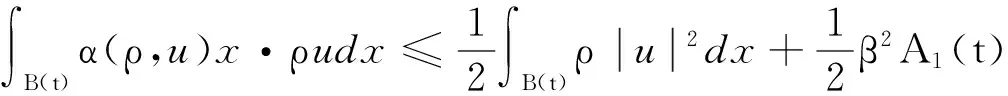
(10)
将式(9)和式(10)代入式(8)就可以化为:
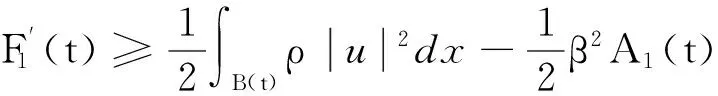
(11)
再由Schwarz不等式得:
(12)
综合式(11)和式(12)得:
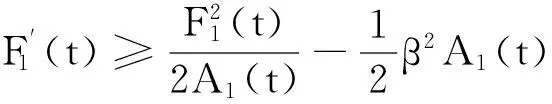
(13)
当0≤t≤τ,式(13)可化为:
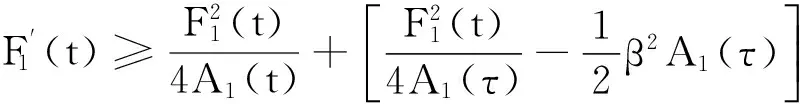
(14)
由定理1中条件可知:

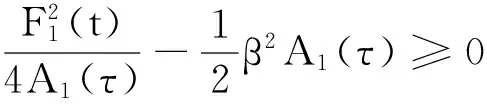
所以式(14)可以改写成:
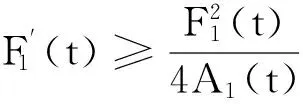
(15)
然后对式(15)两边同时在[0,t]积分,就可得到:
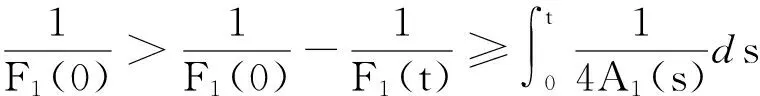
(16)
注:一般情况下考虑0≤α(ρ,u)≤β,从定理1的证明过程中来看,当α(ρ,u)为负值时也成立,称之为反阻尼系数。适当程度下,当初始数据较大时,经典解也必定会在有限时间内爆破。
当m(0)<0时,若F1(0)足够大,同样可以证明初值问题(1)和初始条件(2)的经典解会爆破。
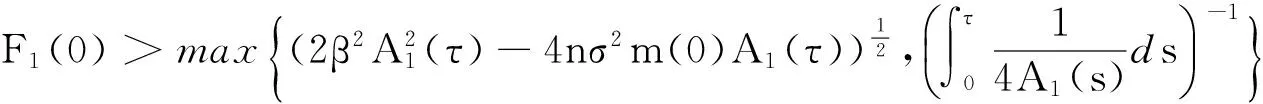
证明一方面,同定理1中式(8),再利用式(10),有:
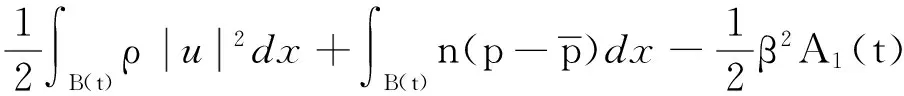
(17)
p′(ρ)=Aγργ-1>0,p″(ρ)=Aγ(γ-1)ργ-2>0。
所以,根据凸函数的性质以及m(0)<0,可得:
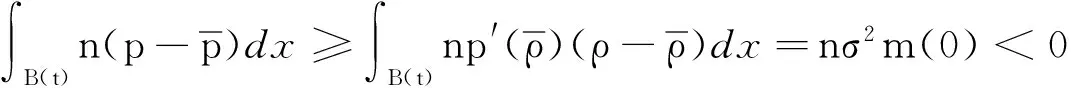
(18)
将式(18)代入到式(17)就可以化为:
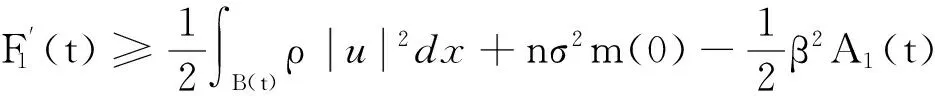
(19)
另一方面,定理1中式(12)仍然成立,即:
(20)
综合式(19)和式(20)得:
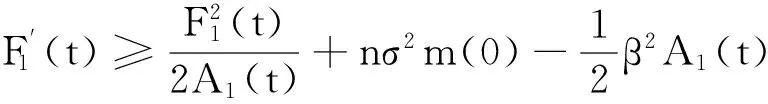
(21)
当0≤t≤τ,式(21)可化为:
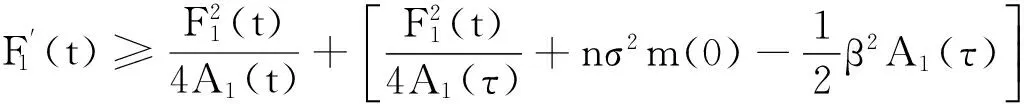
(22)
再根据定理2假设条件可知:

所以式(22)可以改写成:
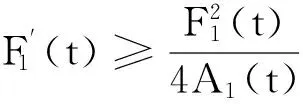
(23)
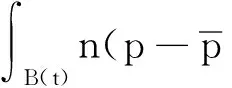
定义:
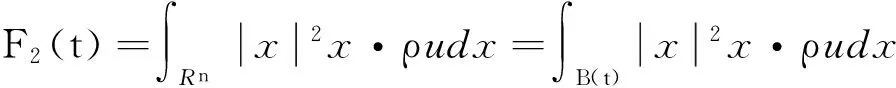
(24)

(25)
定理3若(ρ,u)是初值问题(1)和初始条件(2)在Rn×[0,T)的C1解,若对任意固定的时刻τ>0,满足:
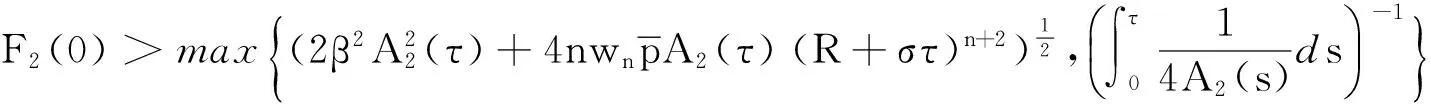
则T<τ。
证明先对F2(t)进行求导,再由初值问题(1),通过分部积分得到:
(26)
其中:
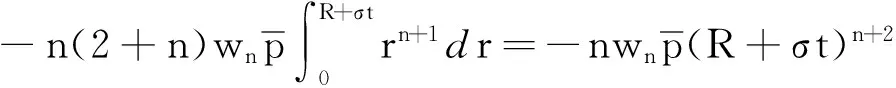
(27)
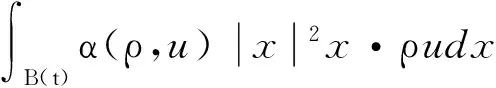
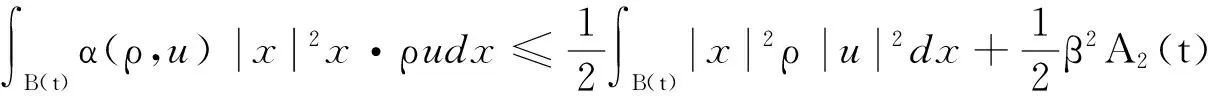
(28)
将式(27)和式(28)代入式(26)可以化为:
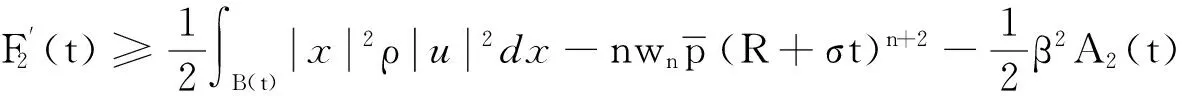
(29)
然后有Schwarz不等式:
(30)
综合式(29)和式(30)得:
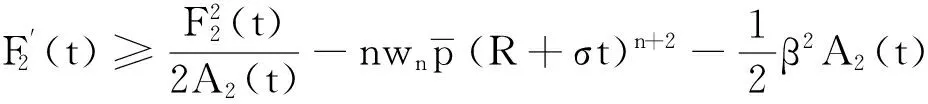
(31)
当0≤t≤τ, 再由定理3假设条件可知,式(31)可以化为:
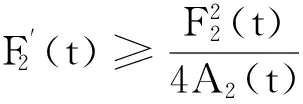
(32)
注:从式(31)开始,也可作如下处理:
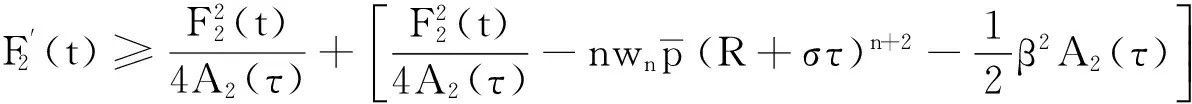
其余证明过程类似,不作赘述,同样可得如下结论:
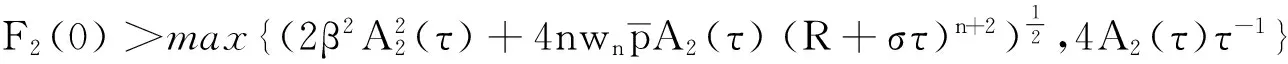
3 结束语
一般采用泛函方法来研究经典解的爆破,即往往是在某些初始数据的泛函较大时证明解必定在有限时间内爆破。当然,根据所提的不同条件也产生了各种不同爆破的结果,其中有些结果还未得到进一步的推广。例如从不带阻尼项到带阻尼项情形的爆破结果还需要完善,尤其带非线性阻尼项的研究成果较少。另外,在有界区域考虑经典解的爆破现象还未建立相关的结论。正因为欧拉方程组在流体力学中占有重要的地位,所以研究可压缩欧拉方程组意义重大。本文通过构造适当的泛函,研究了带非线性阻尼项的可压缩欧拉方程组初值问题的经典解,当初始泛函较大时,证得了经典解必定会在某一时刻前爆破。
[1]SIDERIS T C,THOMASES B,WANG D.Long time behavior of solutions to the 3D compressible Euler equations with damping[J].Communications in partial differential equations,2003,28(3):795-816.
[2]PAN R H,ZHAO K.The 3D compressible Euler equations with damping in a bounded domain[J].Journal of differential equations,2009,246:581-596.
[3]TAN Z,WU G.Large time behavior of solutions for compressible Euler equations with damping in R3[J].Journal of differential equations,2012,252(2):1546-1561.
[4]朱旭生,李芳娥.带非线性阻尼项的三维可压缩欧拉方程组的整体解[J].数学物理学报(A 辑),2014,34(5):1111-1122.
[5]SIDERIS T C.Formation of singularities in three-dimensional compressible fluids[J].Communications in mathematical physics,1985,101(4):475-485.
[6]熊显萍,朱旭生.带非线性阻尼项的欧拉方程初值问题经典解的爆破[J].贵州师范大学学报(自然科学版),2011,29(3):97-99.
[7]LI T,WANG D.Blowup phenomena of solutions to the Euler equations for compressible fluid flow[J].Journal of differential equations,2006,221(1):91-101.
[8]LIANG Z.Blowup phenomena of the compressible Euler equations[J].Journal of mathematical analysis and applications,2010,370(2):506-510.
[9]YUEN M.Blowup for the Euler and Euler-Poisson equations with repulsive forces[J].Nonlinear analysis(theory,methods & applications),2011,74(4):1465-1470.
[10]LI R,LIN X,MA Z,et al.Improved blowup results for the Euler and Euler-Poisson equations with repulsive forces[J].Journal of mathematical analysis and applications,2014,417(1):57-64.
[11]SUZUKI T.Irrotational blowup of the solution to compressible Euler equation[J].Journal of mathematical fluid mechanics,2013,15(3):617-633.
国家自然科学基金项目(61472138,11561024);江西省自然科学基金项目(20151BAB201017)
朱旭生(1968-),男,江西高安人,副教授,博士,主要研究方向为偏微分方程.
2016-03-08
1672-6871(2016)06-0085-06
10.15926/j.cnki.issn1672-6871.2016.06.018
O175.2
A
