高强等边角钢轴压杆局部-整体相关屈曲分析

李清扬，冯圆圆，刘远鹏，李　颖

(河北工程大学 a.土木工程学院；b.建筑设计研究院；c.成人教育学院，河北 邯郸 056038)



高强等边角钢轴压杆局部-整体相关屈曲分析

李清扬a，冯圆圆a，刘远鹏b，李颖c

(河北工程大学a.土木工程学院；b.建筑设计研究院；c.成人教育学院，河北 邯郸 056038)

采用ANSYS有限元软件，考虑初始缺陷和双重非线性，对25根高强等边角钢轴压杆的局部-整体相关屈曲进行了数值分析，得到其局部-整体相关屈曲的极限承载力。分析了不同的肢件宽厚比及屈服强度对局部-整体相关屈曲的极限承载力的影响，利用相关屈曲法推导了高强等边角钢轴压杆的相关屈曲建议公式。分析结果表明：相关屈曲建议公式具有合理性，可为今后的工程设计提供参考。

高强等边角钢；轴压杆；局部-整体相关屈曲；极限承载力；有效屈服强度法；相关屈曲法

0　引言

高强角钢轴压杆可作为输电铁塔主材，在工程中的应用逐渐增多。高强钢构件由于强度增加，宽厚比限值降低，而且存在初始缺陷，使板件更易提前产生局部屈曲。虽然板件的局部屈曲并不意味着构件整体承载力的丧失，但是降低了轴压构件的刚度和整体稳定承载力，导致整体屈曲也容易提前发生。总之，高强钢轴压构件的初始缺陷和超限的宽厚比会促使局部提前屈曲，局部屈曲反过来又会使结构整体较早地丧失承载力[1]。

文献[2-5]对Q420和Q460高强角钢轴压杆的局部稳定性能和整体稳定性能进行了试验。文献[6-8]对Q420高强等边角钢局部稳定性能及整体稳定性能进行了试验，得到其弹性嵌固系数取值、压杆的失稳模式和稳定承载力。文献[9]基于数值计算结果，建议Q420高强等边角钢轴压构件考虑板件局部屈曲相关作用的整体稳定设计方法，但并没有考虑钢材强度对构件稳定性能的影响。近年来，常用有效截面法和有效屈服强度法对局部-整体相关屈曲进行研究[10-12]，而且后一种方法应用更为普遍。文献[13]在文献[12]的基础上，首次提出了相关屈曲法，并给出了适用于焊接薄壁正方箱型截面和长方箱型截面压杆的计算公式，但并未涉及轴压等边角钢的计算。高强角钢宽厚比容易超限，局部屈曲易早于整体屈曲，要继续发展屈曲后强度，就要对高强角钢轴压杆局部-整体相关屈曲进行研究。本文采用ANSYS有限元软件，在考虑整体初始缺陷、局部初始缺陷及双重非线性的情况下，对高强等边角钢轴压杆进行了稳定分析，进而利用相关屈曲法推导了高强等边角钢轴压杆的相关屈曲建议公式，并验证了其合理性。

1　有限元分析

1.1单元类型选择

本文选取SOLID186高阶3维20节点实体单元建立模型[14]。SOLID186单元具有二次位移，适用于模拟不规则网格。该单元每个节点具有x方向、y方向和z方向的位移自由度，并具有塑性、大变形和大应变能力。

1.2模型基本参数及边界约束条件

选用理想弹塑性模型，采用vonMise屈服准则，弹性模量E=206kN/mm2，泊松比ν=0.3，屈服强度和构件尺寸选择名义值。图1为高强等边角钢截面示意图。

图1　高强等边角钢截面示意图

高强等边角钢轴压构件两端设置刚性端板来传递集中荷载。构件两端铰接，模型约束上端、下端端板的x向和y向平动位移，以及下端端板形心节点的z向平动[15]。研究结果表明：Q420高强角钢压杆的经济长细比为0<λ≤80[16]。本文在绕弱轴长细比(λ=40)一定的条件下，分别选取5种不同的肢件宽厚比和屈服强度建立模型，模型各参数如表1和表2所示。

轴压等边角钢不产生局部屈曲的宽厚比限值按下式计算[17]：

(1)

其中:w/t为宽厚比；w为肢件的平板宽度，mm；近似采用w=b-2t，b为边宽度,mm；t为边厚度,mm；fy为名义屈服强度，MPa。

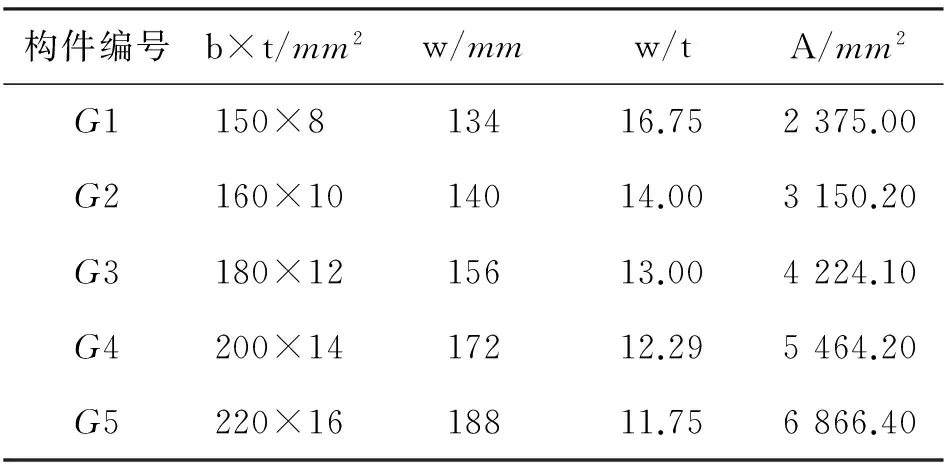
表1　高强等边角钢截面参数

注：b为边宽度；t为边厚度；w为肢件的平板宽度；w/t为宽厚比；A为高强等边角钢截面的面积。

表2　高强等边角钢屈服强度及宽厚比限值

1.3初始缺陷

模型同时考虑构件整体缺陷和板件局部缺陷，构件整体、局部缺陷分别利用模型的第一阶整体和局部屈曲模态的变形乘以相应幅值施加。一般地，整体缺陷幅值取L/1 000，L为构件长度；局部缺陷幅值取b/100，b为板件宽度[18]。文献[19]采用焊接箱型截面有限元模型分析时，通过放大初始几何缺陷来等效残余应力的影响。本文参考文献[19]的方法，通过ANSYS进行试算，取整体缺陷幅值为L/625，局部缺陷幅值为b/50。

1.4双重非线性

模型非线性分析采用弧长法，求解过程考虑双重非线性(材料非线性和几何非线性)。ANSYS中通过采用双线性各向同性强化模型来实现材料非线性，通过打开几何大变形来实现几何非线性。

2　结果与分析

文中模型的局部-整体相关屈曲模态形式都为局部屈曲(变形类似截面扭转)和少量弱轴屈曲的耦合[20]。考虑不同的肢件宽厚比及屈服强度，将有限元非线性分析得到的25根构件的相关屈曲承载力进行整理，结果如表3所示。

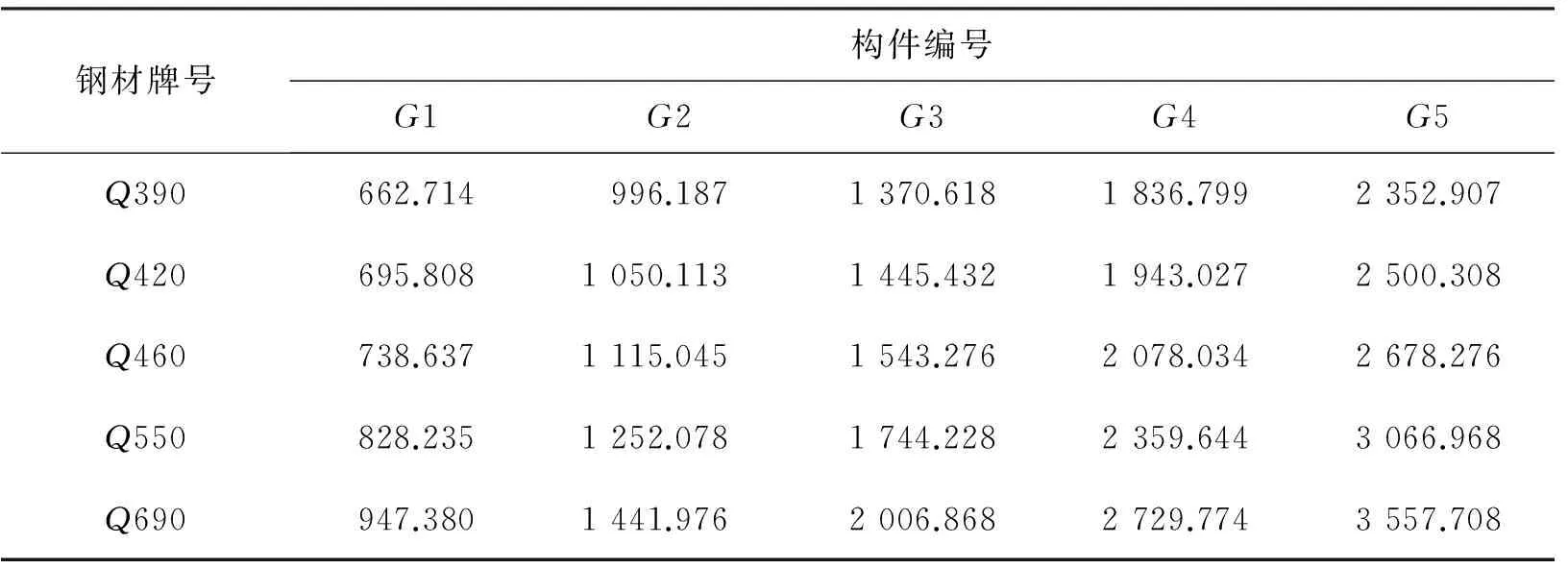
表3　高强等边角钢构件局部-整体相关屈曲承载力　kN

由表3得到不同宽厚比和不同屈服强度的高强等边角钢构件的局部-整体相关屈曲承载力增幅，结果见表4和表5。

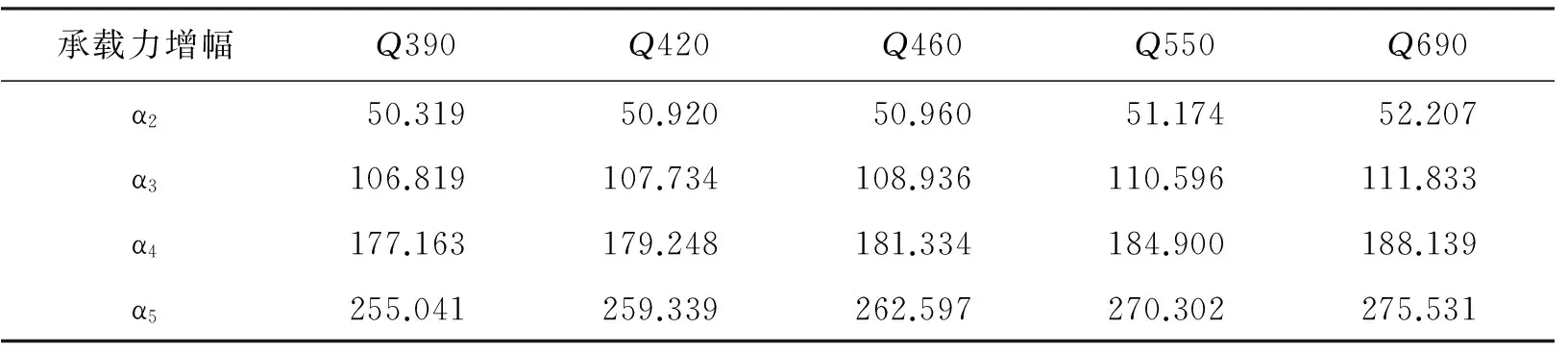
表4　不同宽厚比高强等边角钢构件的局部-整体相关屈曲承载力增幅　%

注：承载力增幅αi=构件Gi与构件G1的相关屈曲承载力差值/构件G1的相关屈曲承载，i=2,3,4,5。

表5　不同屈服强度高强等边角钢构件的局部-整体相关屈曲承载力增幅　%

注：承载力增幅βj=钢材牌号Qj与牌号Q390的相关屈曲承载力差值/钢材牌号Q390的相关屈曲承载力，j=420,460,550,690。

分析表3可知：屈服强度一定，改变肢件宽厚比，构件的相关屈曲承载力随肢件宽厚比的减小呈增大趋势。结合表4分析，屈服强度由390MPa(钢材牌号Q390)增至690MPa(钢材牌号Q690)时，相关屈曲承载力增幅依次增大，说明屈服强度越高，增大趋势越明显。

由表3还可知：肢件宽厚比相同，改变屈服强度，得到构件的相关屈曲承载力随屈服强度增加而变大。结合表5分析，宽厚比从16.75(构件G1)降为11.75(构件G5)时，构件相关屈曲承载力增幅逐渐增大，说明宽厚比越小(超出宽厚比限值越少)，增大屈服强度对提高相关屈曲承载力的效果越明显。

为保证构件的整体稳定承载力，趋向于选择宽肢薄壁的截面，即要有较大的肢件宽厚比，但随之板件的局部稳定承载能力会降低。随着宽厚比的增大，局部屈曲对相关屈曲承载力的削弱作用强于整体稳定承载能力的增强作用时，相关屈曲极限承载力才会减小，可见板件局部屈曲在局部-整体相关屈曲中起控制作用。

3　等边角钢轴压杆的相关屈曲建议公式

3.1有效屈服强度法

宽厚比超限的等边角钢轴压杆承载力，也称杆件的局部-整体相关屈曲承载力或屈曲后强度[17]。计算杆件屈曲后强度的传统方法有两种：有效截面法和有效屈服强度法。文献[12]针对薄壁压杆论证了有效截面法和有效屈服强度法的相通性，两种方法都有一个有效因数ρ，并依据正则化肢件宽厚比λp进行计算，通过比较本文采取第2种方法进行设计。

文献[17]采用有效屈服强度法分析得出，等边角钢轴压杆不产生局部屈曲的肢件宽厚比限值为：

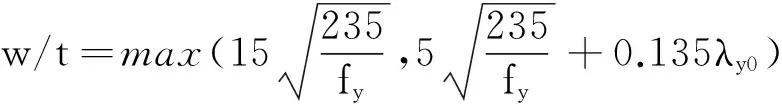
(2)

其中：λy0为角钢绕非对称轴的长细比。

为便于计算，宽厚比限值按照式(1)计算，配合这一限值，有效屈服强度因数为：

(3)

其中：ρ为有效屈服强度因数；λp为正则化肢件宽厚比，且

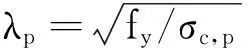
(4)

其中：σc,p为板件弹性屈曲临界应力，N/mm2。对于等边角钢截面轴压杆，则有[17]：

(5)

宽厚比超限的等边角钢轴压杆的承载力为：

N=φAfye，

(6)

其中：A为等边角钢截面面积，mm2；fye为有效屈服强度，MPa,fye=ρfy；φ为稳定因数，用有效屈服强度fye代替fy按a类截面查表[21]求得。

3.2等边角钢轴压杆的相关屈曲建议公式

板件宽厚比超限的轴压杆承载力和其长度有关，而式(3)和式(4)都与杆件长细比无关，不能体现局部与整体的相关关系。为解决该问题，文献[13]进一步提出一种既不同于有效屈服强度法，也不同于直接承载力法的相关屈曲法，并给出了适用于焊接薄壁正方箱型截面和长方箱型截面压杆的计算公式，但未涉及等边角钢截面的轴压杆。本文参考相关屈曲法得出关于等边角钢轴压杆的相关屈曲建议公式，过程如下。

在相关屈曲法中，正则化肢件宽厚比是构件整体屈曲承载力与板件弹性屈曲临界应力之比的平方根。在λp中将压杆稳定因数φ考虑进来，用φfy代替fy，则取代式(4)中λp的新参数λp1为：

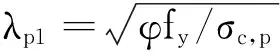
(7)

相应地，等边角钢截面轴压杆的λp变为：

(8)

此时，式(7)中的λp1与杆件的长细比有了联系，便不能再称之为板件的正则化宽厚比，而应该是板件的相关参数[13]。式(7)中根号内是整体屈曲临界应力φfy与局部屈曲临界应力σc,p的比值，体现了局部与整体的相关关系。但是，整体稳定因数φ中包括了初弯曲、初偏心等整体缺陷的影响，而σc,p中却没有局部缺陷的影响，两部分不能协调，λp1取值偏小。现对σc,p做进一步地折减，来考虑局部缺陷影响。经试算，建议折减因数取0.95。此时，式(8)的λp1就变为相关参数λp2：

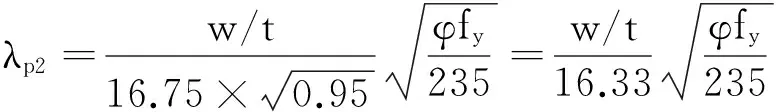
(9)

配合这一参数的有效屈服强度因数相应地修改为：

(10)

此时，等边角钢轴压杆的相关屈曲承载力为：

N=φAρ2fy。

(11)

利用相关屈曲法，在式(11)中考虑了局部与整体的相关关系，故等边角钢轴压杆相关屈曲承载力计算时按常规方法查稳定因数即可，不需要再根据fye去查新的φ值。

为验证相关屈曲建议公式的合理性，现将部分高强等边角钢轴压杆ANSYS有限元计算的稳定因数φa、有效屈服强度法的稳定因数φc1与相关屈曲法的稳定因数φc2进行对比，如表6所示。

表6中的比值φa/(ρ2φc2)相较于φa/φc1，平均值从0.825提高到0.983，且标准差从0.090减小到0.043，效果明显，可见对于宽厚比超限的高强等边角钢轴压杆，相关屈曲法计算的稳定因数与有限元计算所得稳定因数更加吻合，相关屈曲建议公式具有合理性，对高强等边角钢轴压杆的设计与应用具有一定的参考价值。

表6　高强等边角钢轴压杆的φa、φc1与φc2对比

4　结论

(1)屈服强度一定时，构件的相关屈曲承载力随肢件宽厚比的减小而呈增大趋势，且屈服强度越高增大趋势越明显。

(2)宽厚比相同时，构件的相关屈曲承载力随屈服强度的提高而增大，且宽厚比越小(超出宽厚比限值越少)增大效果越明显。

(3)宽厚比越大，板件局部稳定承载能力越弱，构件整体稳定承载能力越强，板件的局部屈曲在相关屈曲中起控制作用。

(4)对于宽厚比超限的高强等边角钢轴压杆，利用相关屈曲法计算所得的稳定因数与有限元计算所得稳定因数更加吻合，考虑局部与整体的相关关系得到的相关屈曲建议公式，可以为高强等边角钢轴压杆的设计与应用提供参考。

[1]钟雯,曹现雷,曹平周.高强角钢塔双肢连接受压主材构件稳定性能研究进展[J].华北水利水电大学学报(自然科学版),2014,35(1):46-50.

[2]张伟.Q420高强角钢轴心受压构件局部屈曲对承载力影响研究[D].西安:西安建筑科技大学,2011.

[3]李天际.高强单角钢受压构件极限承载力的试验与理论研究[D].西安:西安建筑科技大学,2010.

[4]刘盼.高强等边角钢极限承载力及稳定性试验与分析[D].重庆:重庆大学,2008.

[5]孟路希.Q460等边角钢稳定承载力的试验研究[D].重庆:重庆大学,2009.

[6]班慧勇,施刚,刘钊,等.Q420等边角钢轴压杆整体稳定性能试验研究[J].建筑结构学报,2011,32(2):60-67,112.

[7]施刚,刘钊,张勇,等.轴心受压等边角钢构件局部稳定受力性能随钢材强度变化规律的研究[J].工程力学,2012,29(8):129-135.

[8]施刚,刘钊,班慧勇,等.高强度等边角钢轴心受压局部稳定的试验研究[J].工程力学,2011,28(7):45-52.

[9]班慧勇,施刚,石永久.Q420高强度等边角钢轴压构件整体稳定性能设计方法研究[J].工程力学,2014,31(3):63-71.

[10]申红侠,刘翔.高强钢焊接方形截面偏压构件整体和局部相关屈曲承载力分析[J].建筑结构,2014,44(4):35-38,101.

[11]申红侠,赵克祥.Q460高强度钢焊接工字形截面压弯构件局部和整体弯扭相关屈曲有限元分析[J].建筑钢结构进展,2015,17(4):1-9,18.

[12]陈绍蕃.焊接薄壁箱形截面轴心压杆的承载力计算[J].建筑钢结构进展,2009,11(6):1-7.

[13]陈绍蕃.柱段试验与钢压杆的局部-整体相关屈曲[J].建筑钢结构进展,2013,15(2):1-5.

[14]吕静,郭剑,王彬,等.基于ANSYS的角钢局部屈曲/后屈曲等效分析[J].计算机辅助工程,2013,22(6):74-78.

[15]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2007:415.

[16]郭日彩,何长华,李喜来,等.输电线路铁塔采用高强钢的应用研究[J].电网技术,2006,30(23):21-25.

[17]陈绍蕃,王先铁.单角钢压杆的肢件宽厚比限值和超限杆的承载力[J].建筑结构学报,2010,31(9):70-77.

[18]中华人民共和国建设部.钢结构工程施工质量验收规范:GB50205—2001[S].北京:中国计划出版社,2002.

[19]DEGÉEH，DETZELA，KUHLMANNU.InteractionofglobalandlocalbucklinginweldedRHScompressionmembers[J].Journalofconstructionalsteelresearch,2008,64(7):755-765.

[20]陈绍蕃.单角钢轴压杆件弹性和非弹性稳定承载力[J].建筑结构学报,2012,33(10):134-141.

[21]中华人民共和国建设部.钢结构设计规范:GB50017—2003[S].北京:中国计划出版社,2003.

河北省自然科学基金项目(E2010001012)

李清扬(1964-),女,天津人,教授,硕士,硕士生导师,主要从事钢结构的教学、科研和设计.

2015-12-07

1672-6871(2016)06-0061-05

10.15926/j.cnki.issn1672-6871.2016.06.013

TU392.1

A