基于线性工作点的轴向混合磁轴承优化设计与仿真分析

牛立新，周玮琳，付红伟，曹　明

（1.北京航天控制仪器研究所，北京100039；2.第二炮兵工程设计研究院，北京100011）

基于线性工作点的轴向混合磁轴承优化设计与仿真分析

牛立新1，周玮琳2，付红伟1，曹明1

（1.北京航天控制仪器研究所，北京100039；2.第二炮兵工程设计研究院，北京100011）

提出一种利用等效磁路与电磁仿真相结合的方法，实现了基于线性工作点的某磁悬浮CMG轴向混合磁轴承优化设计。通过建立等效磁路及有限元模型实现最佳线性工作点的永磁磁路优化设计。利用Ansoft仿真软件建立电磁参数化仿真模型，实现电磁参数剥离分析及电磁磁路的线性仿真优化设计。以混合磁轴承承载力及刚度线性工作点为约束条件，建立磁轴承动态仿真模型，实现轴向混合磁轴承线性工作区域的动态特性分析。采用该方法设计的磁轴承最大承载力为160N，位移刚度与电流刚度分别在为（-0.5±0.1）×106N/m，（115±3）N/A。与传统混合磁轴承设计相比，该方法设计简单，能够快速实现综合优化设计，在满足承载力前提下，提高了动态力学的线性空间与控制刚度的线性稳定度。

磁悬浮CMG；轴向混合磁轴承；线性工作点；永磁磁路；电磁磁路；仿真优化

0　引言

轴向混合磁轴承是磁悬浮控制力矩陀螺（Control Moment Gyroscope，CMG）的核心部件之一，其混合结构型式主要由永磁磁路和电磁磁路结构组成，并通过磁场耦合来实现一定角动量的飞轮转子轴向自由度控制［1］。由于CMG的安装形式和应用环境限制，对轴向磁轴承尺寸及性能要求严格。

针对典型的磁轴承系统，朱煌秋［2］及赵旭升［3］等利用传统的电磁理论，提出以最大磁能积为出发点进行了混合磁轴承设计；孙津济［4］、房建成［5］等通过基于网络磁路方法进行以承载力为出发点的混合磁轴承结构设计；王曦［6］、侯二永［7］及Bachovchin K.D.［8］等提出磁轴承混合磁路解耦设计方法；刘虎［9］及Takayuki T.［10］讨论了基于积分方法精确计算磁阻的混合磁轴承动力学设计方法。研究表明，以不同设计角度为出发点会使磁轴承性能发生一定变化，单一设计变量最优往往会限制整体参数实现优化，并且复杂等效方程的多参数电磁解耦，会降低参数解耦精度，进而影响磁轴承动态特性。

因此，本文在上述研究的基础上，以轴向混合磁轴承的线性工作点为设计出发点，以承载力为约束条件，磁轴承动态性能为最终优化目标，综合考虑永磁磁路、电磁磁路工作磁密的线性区域，通过等效磁路和数值参数化仿真相结合方法实现了高线性度的磁轴承仿真优化设计。

1　轴向混合磁轴承结构

采用永磁混合磁轴承的某五自由度内转子系统结构示意如图1所示，系统主要由电机、位移传感器、转子组件、径向磁轴承及轴向磁轴承组成，电机驱动转子组件对外提供一定角动量，径向磁轴承和轴向磁轴承分别提供径向扭动控制力矩、径向平动及轴向平动控制力，位移传感器检测转子悬浮动态位移。

轴向磁轴承的结构及磁路如图2所示，由轴向磁轴承座、磁轭、永磁体及线圈构成，其混合磁结构在转子组件两侧呈圆环扁平形状。磁轴承的混合磁路分为两部分，一部分为永磁磁路，由永磁体产生的偏置磁通，大部分穿过悬浮气隙及飞轮转子形成闭合偏置回路，其他则在第二气隙分流直接闭合形成漏磁磁路；混合磁路的另一部分为电励磁磁路，依靠线圈产生调节磁通，分别经由第二气隙和永磁体与悬浮气隙闭合调节磁路。控制系统通过改变调节磁通强弱及方向，使飞轮转子一侧混合磁场的磁密增强，另一侧混合磁场的磁密减弱，进而实现飞轮转子的精确悬浮控制。

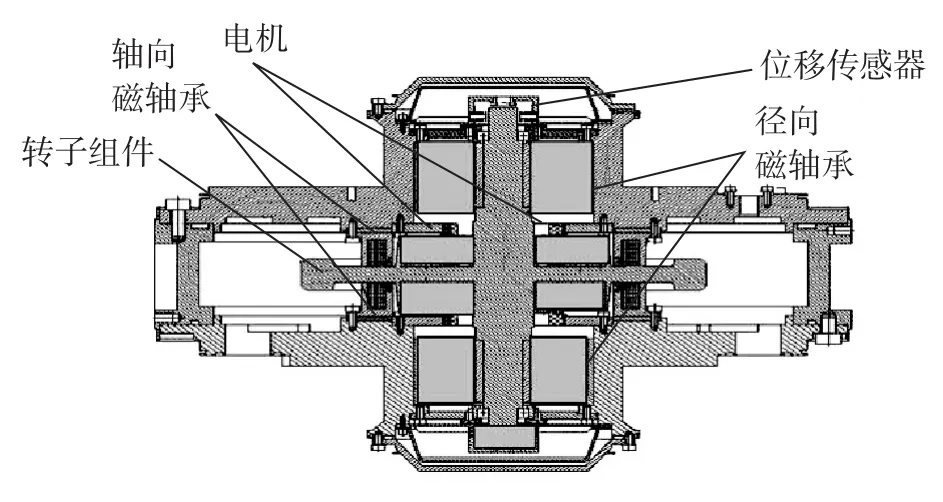
图1　五自由度内转子系统结构示意图Fig.1　Construction of active magnetic suspension rotor system with five dimensionalities

2　永磁磁路最佳工作点优化设计

2.1线性工作点设计与分析

磁性材料自身的饱和磁化特性，使混合磁路中磁密不能随磁场的增大而无限增大。图3所示为某磁性材料B-H磁化曲线，在0T～1.5T区间，磁感应强度随外界磁场增强呈线性增长；1.5T后，材料趋于饱和，磁密与磁场呈非线性变化。

在使用时，通过设置横杆2，当需要清理白板1的版面时，通过移动横杆2到适当的位置，下压把手16，带动横杆2向下运动，可使圆筒擦8和方擦15与白板1接触，通过设置圆筒擦8两侧的方擦15，可三重清理白板1的表面，从而达到清理白板1表面更加干净的目的，通过设置固定块3和滑块4，使横杆2的移动更加稳定、快速和方便，通过设置固定杆9底部的滚轮11与滚槽10，不仅可支撑横杆2，且使横杆2的移动更加稳定，且通过设置限位弹簧7，在不需要清理时，圆筒擦8与白板1不接触。

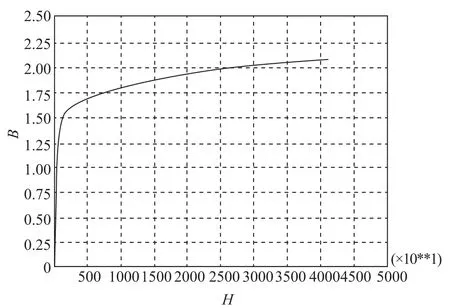
图3　软磁材料B-H磁化曲线Fig.3　B-H magnetized curve of soft magnetic property

理论上，要使磁轴承具有良好动态力学性能，磁轴承工作磁密需工作在材料的线性区间内，当磁轴承承载力最大时，磁轴承气隙磁密相叠加的一边磁感应强度达到最大值Bm，抵消的一边达到最小值0。当转子处于平衡位置时，定、转子之间各气隙处的磁感应强度相等，等于永磁磁路提供的偏置磁感应强度Bp，Bp=Bm/2，那么，材料饱和磁感应强度为Bm=1.5T，故应取永磁磁路磁密的线性工作点为Bp=0.6T～0.8 T。

2.2基于线性工作点的永磁磁路设计

以永磁磁路的线性工作点为设计出发点，建立基于线性工作的BP为初值的等效磁路方程（式（1））。图4所示为永磁等效磁路。

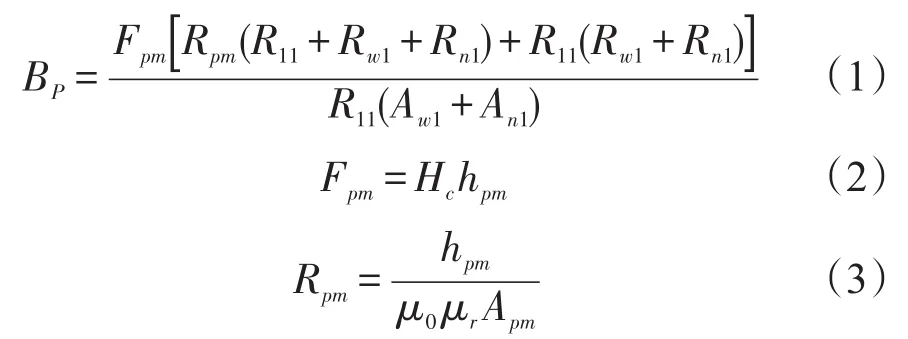
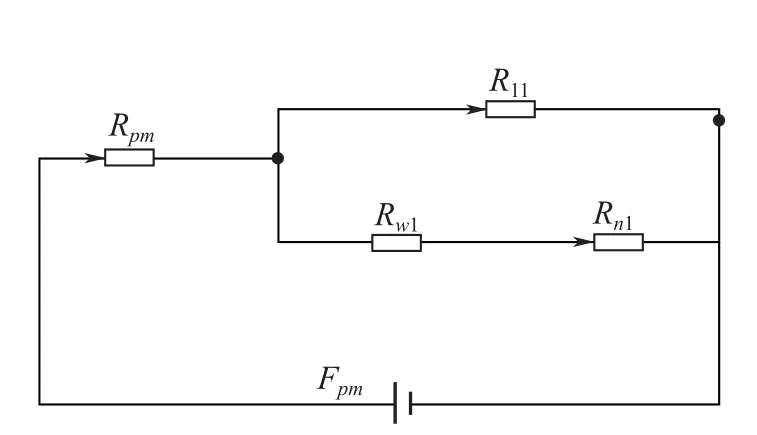
图4　永磁等效磁路Fig.4　Equivalent circuit of permanent magnet

其中，BP为永磁体工作气隙磁密，Hc为永磁体的矫顽力，hpm为永磁体磁化方向长度，Rpm为永磁体磁阻， Apm为永磁体横截面积，An1为内圆端面横截面积，Aw1为外圆端面横截面积， μ0为真空中磁场常数， μr为相对磁导率，R11为第二气隙磁阻，Rw1为外圆端面处磁阻，Rn1为内圆端面处磁阻。

综合式（1）、式（2）和式（3）线性工作点下永磁体轴向长度hpm与截面积Apm的关系，如式（4）所示。

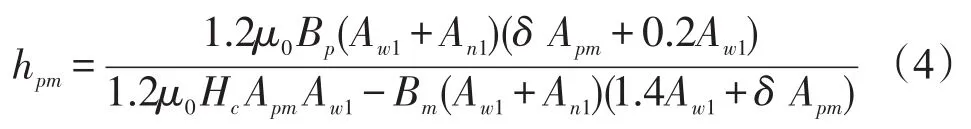
其中，δ为工作气隙。

图5所示为永磁体轴向长度hpm在1mm～10mm 的hpm-Apm关系曲线，选取满足永磁磁路线性工作点的磁钢充磁长度 hpm=3mm，横截面积为Apm=1.6×10-4m2。

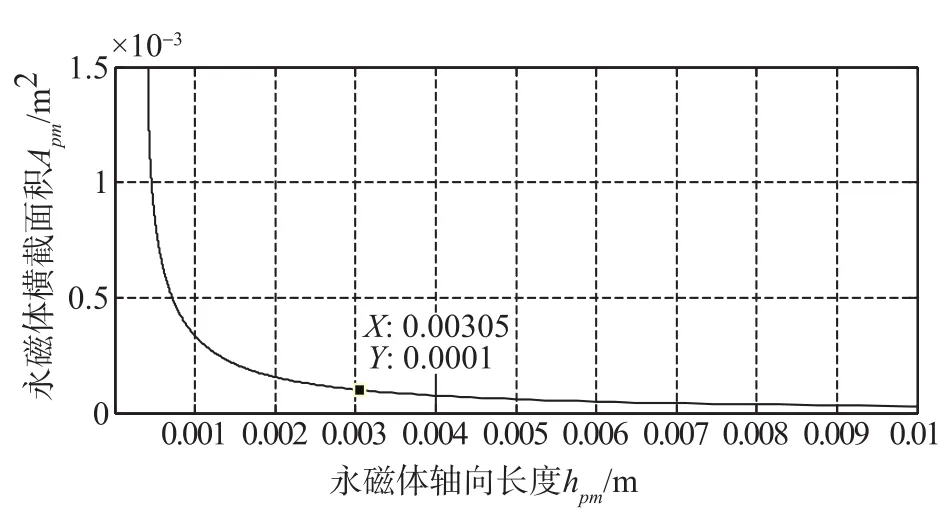
图5　永磁体hpm-Apm参数关系曲线Fig.5　Relationship between hpmand Apmof permanent magnet steel

2.3永磁磁路参数优化设计与仿真分析

建立轴向磁轴承轴向对称二维有限元模型，图6所示为永磁磁路在第二气隙处及工作气隙处磁路分流产生漏磁，使实际工作气隙增大，影响了气隙磁阻系数。

图6　永磁体磁力线分布Fig.6　Magnetic figure of permanent magnetic circuit

图7所示为磁路等效云图仿真计算结果，永磁体漏磁主要发生在第二气隙处，漏磁系数σpm=1.5，进而得到磁阻系数 f=1.065。

图7　永磁体磁场强度分布Fig.7　Permanent magnetic field contours

式（5）为永磁体参数补偿方程，优化补偿后永磁体h'pm≈3.2mm，A'pm≈2×10-4m2。

永磁磁路线性补偿值进一步验证，等效磁路方程（式（1））与永磁特性曲线方程（式（6））联立可以得到图8所示工作点P（0.78T，200KA/m）。平衡位置永磁偏置状态，永磁磁路的工作磁密为0.78T，满足线性工作点区域约束。

其中，B为永磁体磁密；H为外界磁场强度。

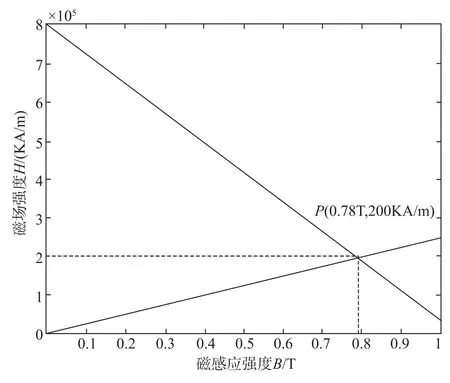
图8　永磁磁路最佳工作点曲线Fig.8　Advanced work-point of permanent magnetic circuit

3　电磁磁路参数仿真化优设计

混合磁路是调节磁场和永磁磁场的耦合，一般选取混合工作磁密在磁化曲线线性段的中点范围为宜，从而要求小电流调节磁场控制方法，保证即使电励磁磁场中流过最大电流时磁路结构中也不会出现饱和现象。然而，调节磁场优化及混磁磁路解耦一直是理论设计难点，本文提出利用仿真方法，以线圈安匝数为单参变量建立动态仿真模型，并通过参数分析过程，实现电磁调节磁路优化分析。

图9所示为Ansoft软件中建立的轴向混合磁轴承二维轴对称模型，并定义方框内为线圈模型，设置线圈安匝数为10A～300A范围内的连续电磁激励。图10所示为连续电磁激励下的混合磁轴承承载力变化曲线，在该电磁激励下，承载力变化范围为90N～260N，随电流增加近似正比例递增。图11为安匝数为150A时，磁轴承混合磁场磁密分布云图，磁路主要磁通在0.7T～1.2T范围，内端面工作气隙磁密为0.62T，外端面工作气隙磁密为0.56T。仿真结果表明，当安匝数为150A时，磁路线性工作点良好，承载力为160N。

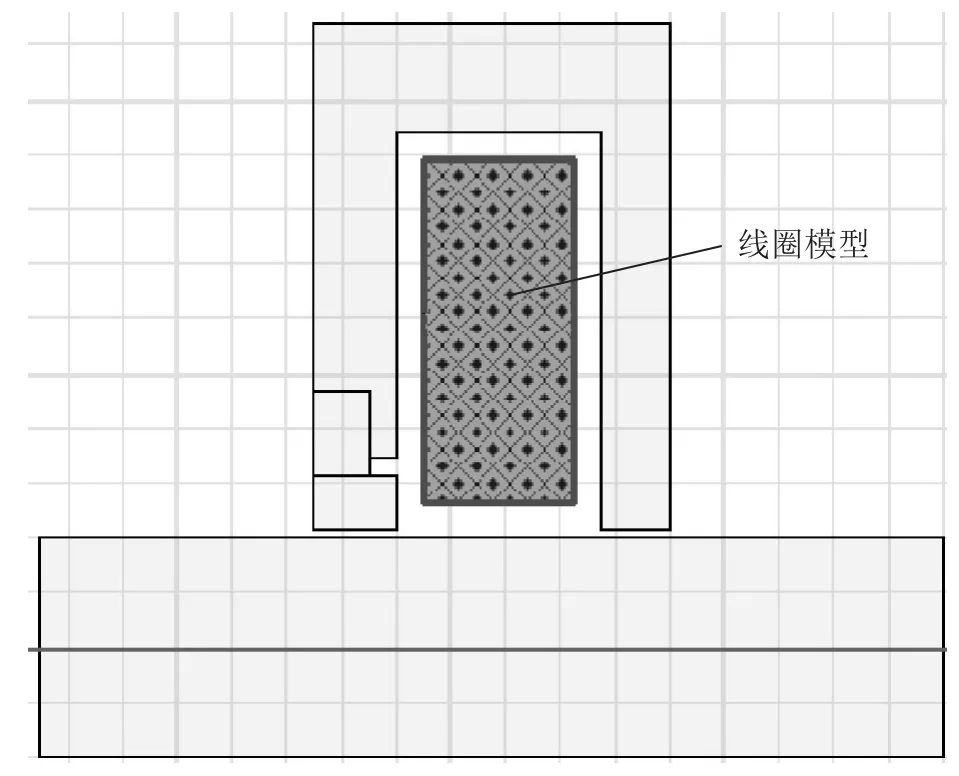
图9　电磁仿真模型Fig.9　The model of EM simulation

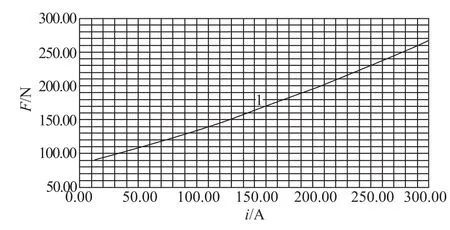
图10　安匝数与承载力对应曲线Fig.10　Relationship curve of between NI and load capacities

电磁参数不仅影响磁路结构线性工作点，同时，线圈电感效应还会影响控制电流产生的力对时间的变化率，控制电流会受到电感影响或被延迟。因此，本文还采用仿真计算方法，对线圈电感值进行参数求解。图12所示为电感随不同线圈参数的单递增规律，在控制指标要求下，式（7）可以给出一定电感对应的线圈匝数。

其中，L为线圈电感。

最终确定线圈匝数N=300匝，最大调节电流i=0.5A。

4　混合磁轴承动力学线性仿真分析

图13（a）和图13（b）分别表明磁轴承承载力与位移、电流呈非线性变化关系曲线， kδ与ki为曲线在点（i0，δ0）一阶微分线性化处理得到的曲线斜率，由承载力曲线可以看出，非线性总是使平衡位置趋于不稳定。但对于控制系统而言，总希望在点（i0，δ0）处实现线性控制。因此，转子动态承载力模型在状态空间内利用泰勒级数展开，并以线性微分方程形式给出式（8），其中，导数kδ与ki也代表了磁轴承在该位置的位移刚度和电流刚度。很显然，磁轴承动态承载力是在小振幅条件下，即系统工作在线性或非饱和区成立，所以控制刚度必须基于此前提。对于点（i0，δ0）的刚度系数是随点的变化而变化的，因此，需要对磁轴承承载力的线性区域以及动态控制线性区域进行动力学分析。

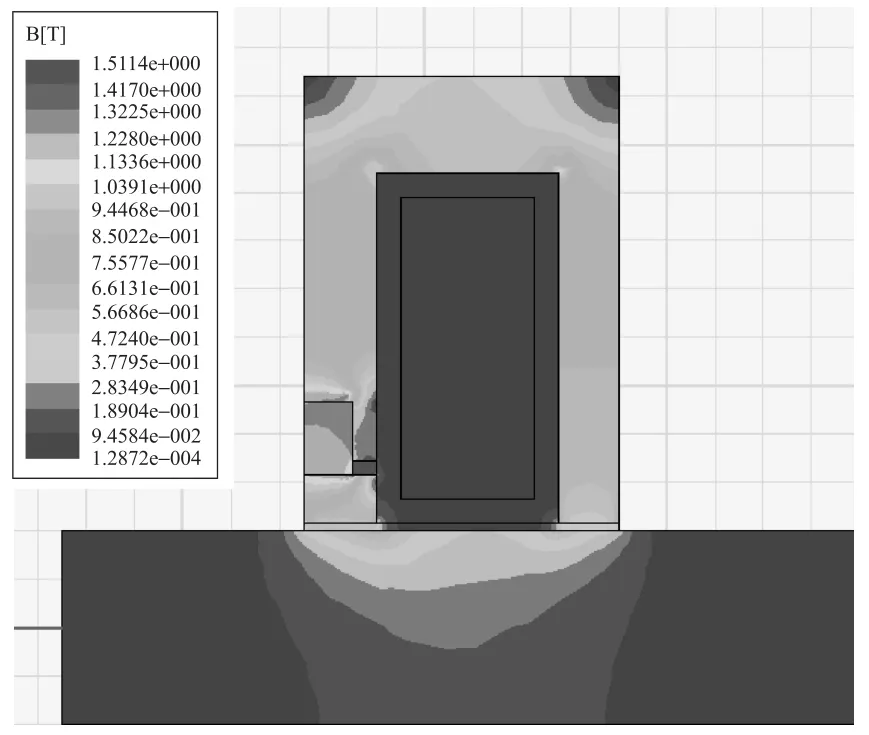
图11　150A时磁密分布云图Fig.11　Permanent magnetic field contours with 150A （NI）

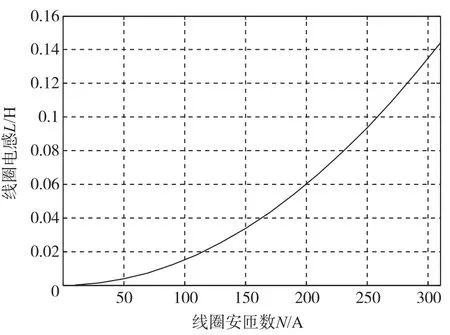
图12　不同线圈参数下电感变化曲线Fig.12　Inductance curve of field coil with different number of circles

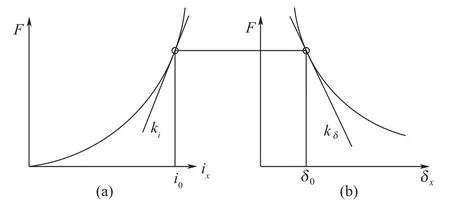
图13　承载力与位移刚度Ki、承载力与电流Kx关系曲线图Fig.13　Relationship between load capacity and motional stiffness/between load capacity and current stiffness

建立磁轴承动态力学仿真模型如图14所示，转子两侧分别建立对称的磁轴承模型。转子工作间隙在-0.3mm～0.3mm区域内连续动态变化时，转子偏置力变化曲线如图15所示。混合磁轴承磁力随着位移的增加而减小（相对平衡位置），位移在-0.3mm～-0.2mm和0.2mm～0.3mm区域内呈非线性变化，在-0.2mm～0.2mm区域内呈线性变化，磁轴承承载力满足线性要求。在线性区域对磁轴承位移刚度进行求解如图16所示，位移刚度为（-0.5±0.1）×106N/m，位移刚度波动幅值较小，位移刚度具有良好的稳定度。

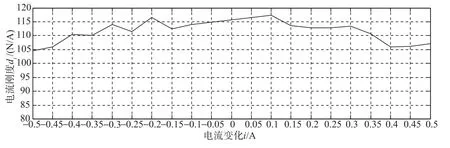
图17所示为电流激励在-150A～150A安匝数连续变化下，混合磁轴承承载力与电流正比线性关系。在匝数已知前提下，电流在-0.5A～0.5A范围内对电流刚度进行求解，如图18所示，电流在-0.5A～0.5A范围内，电流刚度波动幅值较小，平衡位置电流刚度在（115±3）N/A范围内，电流刚度具有良好的稳定度。

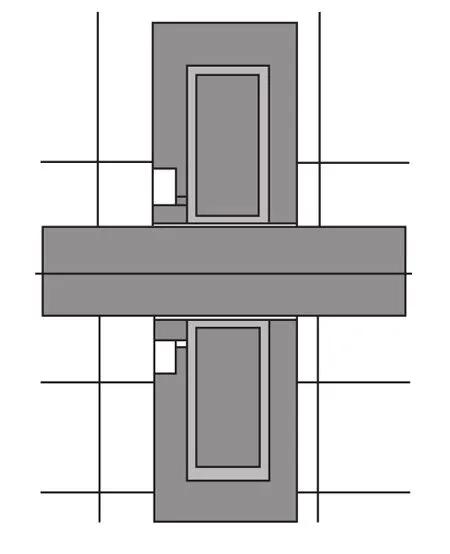
图14　二维磁轴承轴对称动力学仿真模型Fig.14　Dynamics analysis of magnetic bearing simulation model

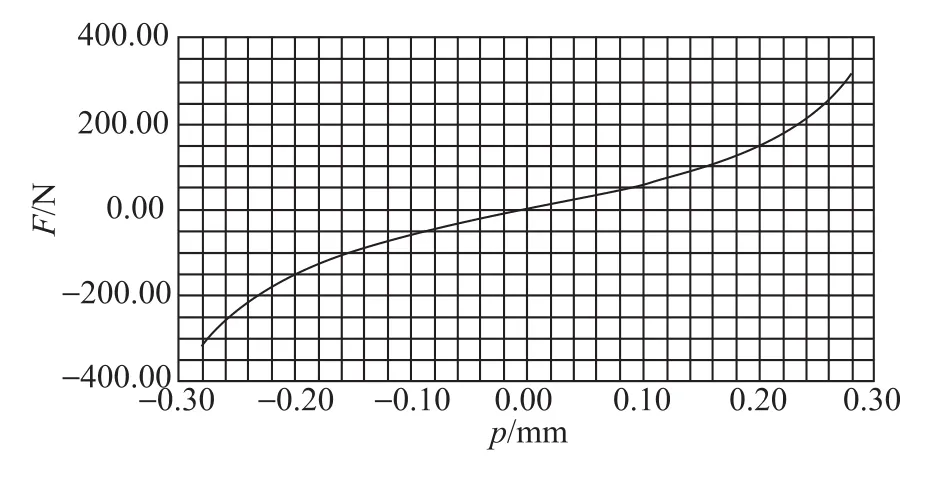
图15　位移与偏置力关系曲线Fig.15　Relationship between motion and magnetic force

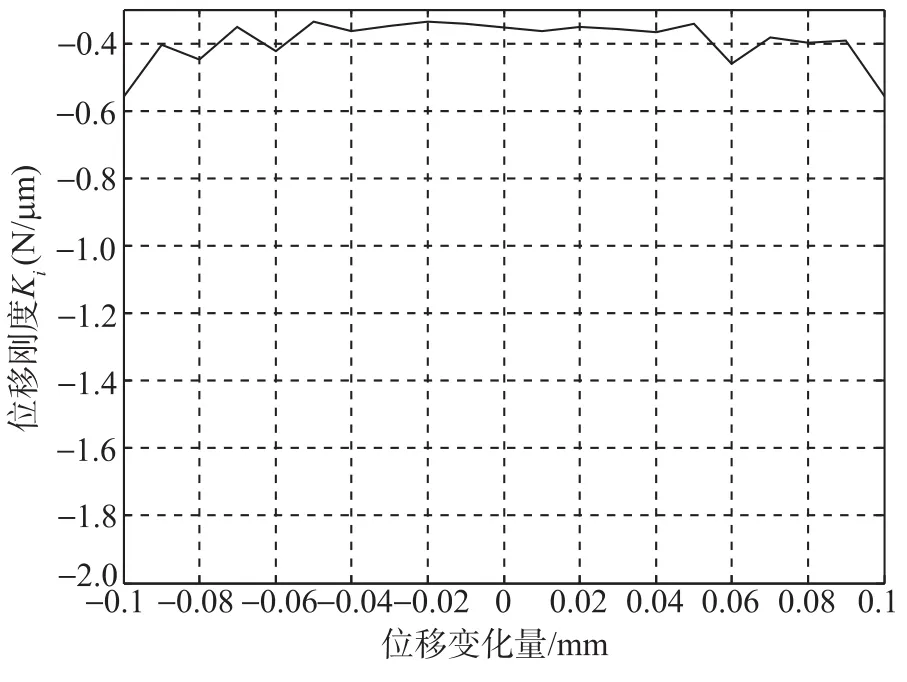
图16　位移刚度随位移变化曲线Fig.16　Relationship between motional stiffness and motion

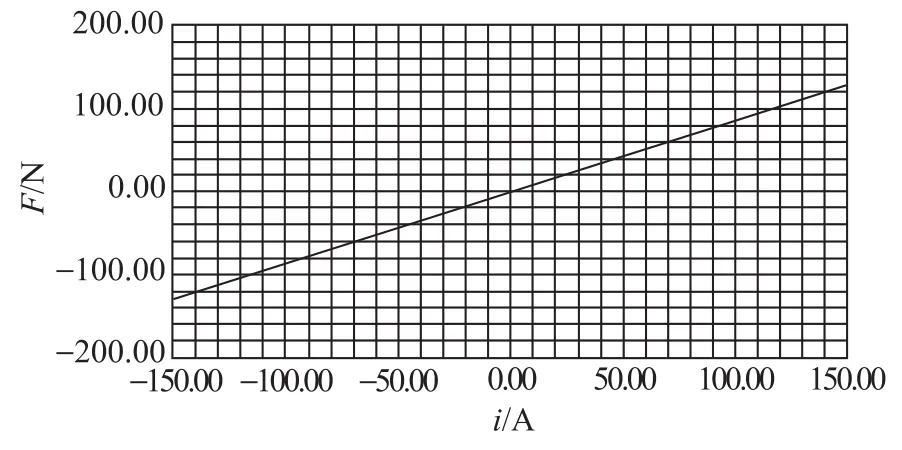
图17　安匝数与力关系曲线Fig.17　Relationship between the number of circles and magnetic force

动态仿真分析结果表明，基于线性工作点优化设计的轴向混合磁轴承，在-0.2mm～0.2mm位移区间内的承载力具有良好线性度，相比可控区域提高了1倍的线性范围，同时，整个调节电流区间，磁轴承混合承载力具有良好线性动态特性。

5　设计方法对比分析

传统磁轴承设计方法是以永磁磁路的磁钢最大磁能积为设计出发点，并以磁轴承承载力来约束设计参数，同样，磁性材料的饱和磁密限制了磁路搭建，建立好磁路后，根据气隙长度来求解永磁体对外磁动势，并根据磁路计算及永磁体退磁曲线确定最大磁积能时永磁体横截面积和充磁长度，最后通过校验方式确定磁路磁密分布，进而完成永磁磁路设计。同时，根据永磁磁路分布情况，以最大承载力及饱和磁密为约束条件，进行线圈参数确定，完成电磁磁路设计。此过程中，由于磁钢尺寸已定，磁路结构和工作气隙磁密是被动设计，在混合磁轴承设计，利用式（1）与式（6）联立永磁工作方程与退磁曲线方程，得到离散数据如表1所示。同样承载力设计指标下，为了追求最大磁能积，会导致永磁体充磁长度趋于小值，横截面积趋于大值。另外，结合图19和图20，从偏置承载力与位移关系可以看出，偏置承载力线性范围为-0.1mm～0.1mm，同时，位移刚度在-0.08mm～0.8mm范围内衰减。

通过仿真计算，得出表2磁轴承基本性能参数对比表，很明显，基于永磁体最大磁能积设计方法，磁钢尺寸难以满足加工的要求；偏置力线性区间明显减小，并且，同样位移区间内，位移刚度值波动较为明显。

基于最佳工作点的磁轴承线性模型以线性化性能为首要考虑因素，不考虑永磁输出效率，这样会造成磁能的浪费。在实际应用过程中，由于磁钢采用分块拼接方式，以及装配精度影响，往往会出现磁中心偏离几何中心，实际数据会小幅度偏离线性模型设计值，需要产品整机装配后进行磁中心实验校正，来补偿实际参数差值，此过程牺牲悬浮间隙的余量，降低了控制系统可靠性。

图18　电流刚度随电流变化曲线Fig.18　Relationship between current stiffness and current

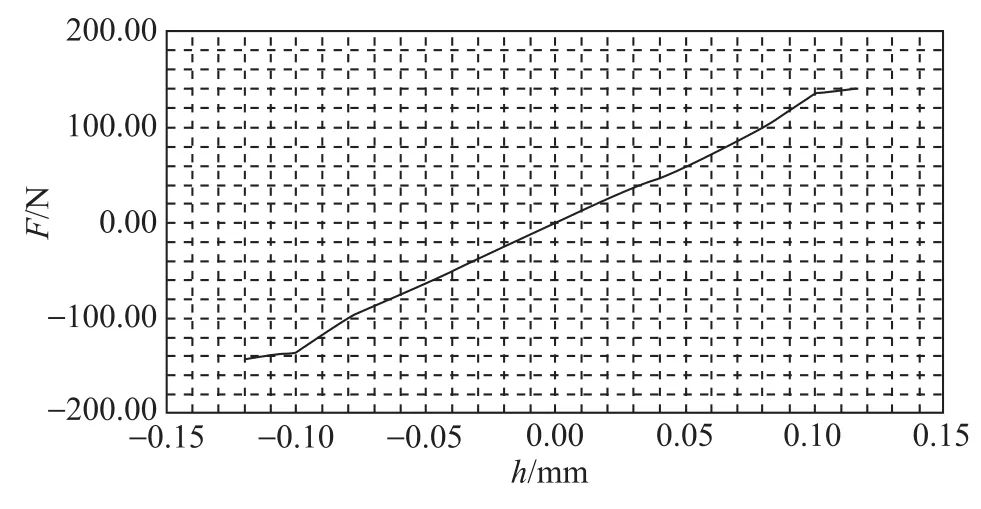
图19　永磁最大磁能积设计的偏置力线性图Fig.19　Biasing magnetic force according to design of max HB

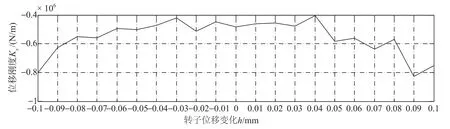
图20　永磁最大磁能积位移刚度分析Fig.20　Motional stiffness according to design of max HB

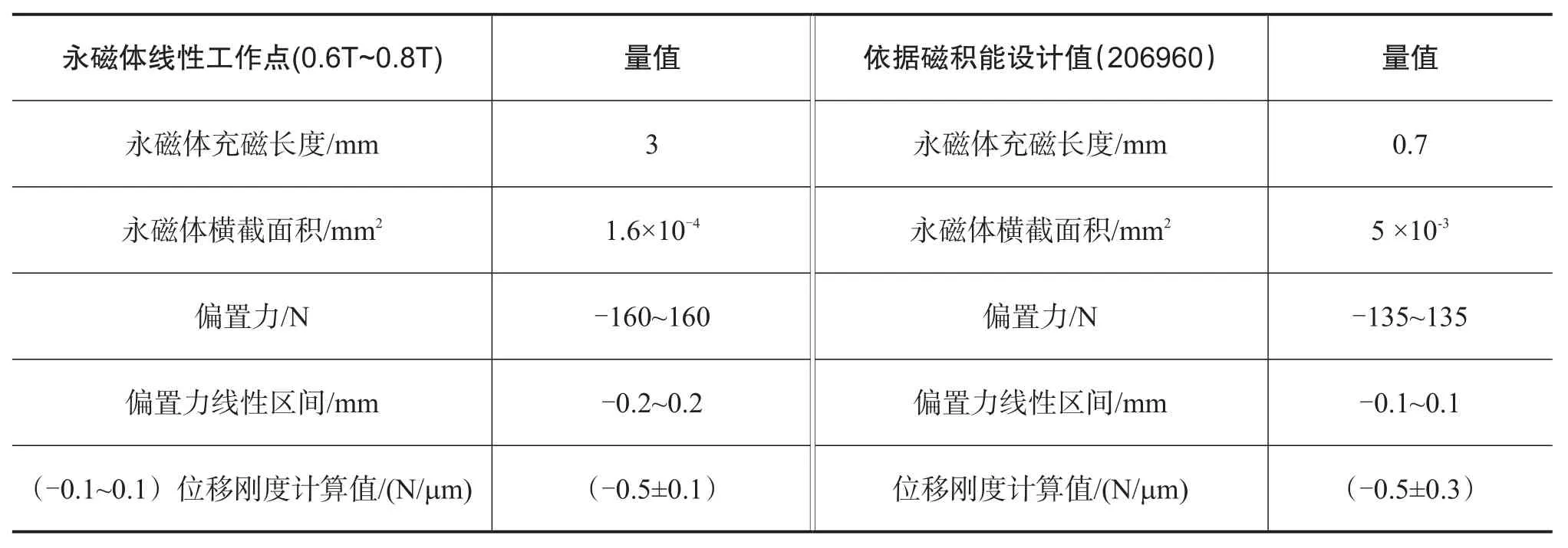
表2　磁轴承性能对比表Table 2　Comparison of magnetic bearing performance

6　结论

本文提出基于线性工作点的轴向混合磁轴承设计思路，利用等效磁路方法与数值仿真分析方法，进行了永磁磁路永磁参数优化补偿、电磁磁路电磁参数剥离分析和磁轴承动力学特性分析，分析和仿真结果表明：

1）该方法设计的磁轴承最大承载力为160N，设计线性工作点为0.6T～0.8T，优化计算结果为0.78T，提高了产品设计的精度、准确性。

2）该方法设计的磁轴承位移线性区域为-0.2mm ～0.2mm（相对平衡位置），调节电流为全区域线性，控制系统的位移刚度和电流刚度分别为（-0.5± 0.1）×106N/m，（115±3）N/A，提高了动态力学的线性区域，保证了磁轴承动态承载力与磁极气隙和控制电流间具有良好的线性关系，进而提高控制系统线性度。

［1］房建成，孙津济，樊亚洪.磁悬浮惯性动量轮技术［M］.北京∶国防工业出版社，2012. FANG Jian-cheng，SUN Jin-ji，FAN Ya-hong.Magnetically suspended inertial momentum wheel technology ［M］.Beijing∶National Defense Industry Press，2012.

［2］朱熀秋，张仲，诸德宏，等.交直流三自由度混合磁轴承结构与有限分析［J］.中国电机工程学报，2007，27（12）∶79-81. ZHU Huang-qiu，ZHANG Zhong，ZHU De-hong，et al. Structure and finite element analysis of an ac-dc threedegrees of freedom hybrid magnetic bearing［J］.Proceedings of the CSEE，2007，27（12）∶79-81.

［3］赵旭升，邓智全，汪波.永磁偏置径向磁轴承的原理分析与参数设计［J］.电工技术学报，2011，26（11）∶127-134 ZHAO Xu-sheng，DENG Zhi-quan，WANG Bo.Principle analysis and parameter design of permanent magne bias radial magnetic bearing［J］.Transactions of China Electrotechnical Society，2011，26（11）∶127-134.

［4］孙津济，房建成，王曦，等.一种新型结构的永磁偏置径向磁轴承［J］.电工技术学报，2009，24（11）∶53-60. SUN Jin-ji，FANG Jian-cheng，WANG Xi，et al.A new permanent magnet biased radial magnetic bearing［J］. Transactions of China Electrotechnical Society，2009，24（11）∶53-60.

［5］房建成，孙津济.一种磁悬浮飞轮用新型永磁偏置径向磁轴承［J］.北京航空航天大学学报，2006，32（11）∶1304-1307. FANG Jian-cheng，SUN Jin-ji.New permanent magnet biased radial magnetic bearing in magnetic suspending flywheel application［J］.Journal of Beijing University of Aeronautics andAstronautics，2006，32（11）∶1304-1307.

［6］王曦，房建成，樊亚洪，孙津济.轴向力偏转五自由度永磁偏置磁轴承及磁路解耦设计［J］.中国电机工程学报，2011，31（17）∶91-98. WANG Xi，FANG Jian-cheng，，FAN Ya-hong，SUN Jinji.Axial force tilting permanent-magnet-biased magnetic bearing with five degrees of freedom and magnetic field decoupling design［J］.Proceedings of the CSEE，2011，31 （17）∶91-98.

［7］侯二永，刘昆.混合磁轴承磁场与磁力解析计算［J］.机械工程学报，2012，48（6）∶193-198 HOU Er-yong，LIU Kun.Analytical calculation of magnetic field and forcefor hybrid magnetic bearing［J］.Chinese Journal of Mechanical Engineering，2012，48（6）∶193-198.

［8］ Bachovchin K D，Hoburg J F，Post R F.Magnetic fields and forces in permanent magnet levitated bearings［J］. IEEE Transactions on Magnetics，2012，48（7）∶2112-2120.

［9］刘虎，房建成.新型永磁偏置轴向磁轴承的磁力特性［J］.机械工程学报，2010，46（8）∶167-174 LIU Hu，FANG Jian-cheng.Magnetic force characteristics of a novel permanent magnet biased axial magnetic bearing［J］Chinese Journal of Mechanical Engineering，2010，46（8）∶167-174.

［10］ Takayuki T，Nobuyuki K，Takeo I.Design and simulation of a five degrees of freedom active control magnetic levitated motor［J］.IEEE Transactions on Magnetics，2013，49（5）∶2257-2262.

Design Method ofActive Magnetic Bearing for Advanced Mid-point of Linear Range

NIU Li-xin1，ZHOU Wei-lin2，FU Hong-wei1，CAO Ming1
（1.Beijing Institute ofAerospace Control Devices，Beijing 100039；2.The SecondArtillery Engineering Design and Research Institute，Beijing 100011）

This paper introduced an optimal design method of designing active magnetic bearing according to the formulae of equivalent magnetic circuit and EM simulation analysis.Depending on the method，it’s possible to get magnetic bearing worked at advanced mid-point of linear range.The formulae of magnetic circuit and the EM simulation model were established based on the bearing worked at the mid-point.Then the optimal design was done through the optimization of magnetic circuit，field coil and the constraint condition of load-carrying capacity and stiffness with Ansoft. It was successfully realized that the max load-carrying capacity of magnetic bearing is 160N，motional stiffness and current stiffness are（-0.5±0.1）×106N/m and（115±3）N/A.Compared with traditional design method，it is more efficient and reliability to design the magnetic bearing.The result shows that it can improve the linear range of dynamic property and stabilization of magnetic suspension.

magnetically suspended control moment gyro；active magnetic bearing；mid-point of linear range；permanent magnetic circuit；electronic magnetic circuit；advanced simulation

TH133.3

A

1674-5558（2016）03-01088

10.3969/j.issn.1674-5558.2016.02.015

2015-03-16

航天科技集团公司工艺研究项目（编号：ZDGY2013-62）

牛立新，男，机械电子工程专业，硕士，工程师，研究方向为磁悬浮惯性执行机构电磁设计与结构设计。