海洋钢结构尺寸误差分析新方法

孟令河，秦野，王建喜，王智洪，王雪莲海洋石油工程股份有限公司，天津300452

海洋钢结构尺寸误差分析新方法

孟令河，秦野，王建喜，王智洪，王雪莲
海洋石油工程股份有限公司，天津300452

海洋钢结构精度是反映钢结构建造的一项重要指标，传统海洋钢结构精度分析方法是通过对比实际测量尺寸与理论尺寸的差值反映钢结构的误差，这种方式简单却不够直观，不利于施工人员进行尺寸的调整。运用最小二乘坐标拟合技术，使实测数据最优匹配设计数据，并使钢结构的尺寸误差以三维偏差的大小和方向表示，直观合理，并利用AutoCAD VBA编写计算程序，快速计算出偏差值，对现场施工调整及误差评估具有很好的作用。

最小二乘法；坐标拟合；设计数据；实测数据；三维精度

1 传统海洋钢结构精度分析方法

传统海洋钢结构精度分析方法是通过对比实际测量尺寸与理论尺寸的差值来判断结构精度是否满足要求，这种方法虽可以判断简单的结构尺寸，但是对于复杂结构，就很难反映各个测量点的偏差，而且不利于施工方调整尺寸。以某导管架形式的钢结构为例，如需全面反映该钢结构的制造误差，需要用多个尺寸表示，如图1所示。如某一尺寸超出误差允许范围，则调整这个节点时需要综合考虑是否会影响相邻尺寸或者对角尺寸等，调整的方向和大小都很难判断。

2 新的海洋钢结构精度分析方法

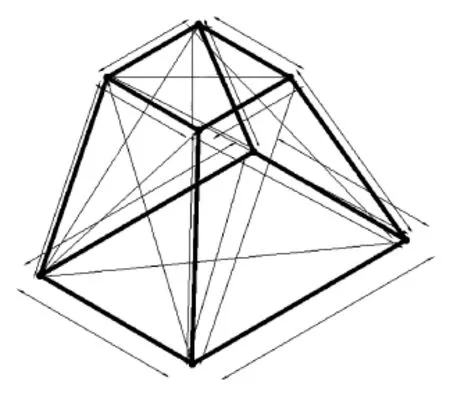
图1　钢结构三维尺寸示意

本文介绍了一种坐标拟合技术，通过最小二乘法使实测点最佳匹配理论数据，即所有偏差值之和为最小，使各个节点的三维偏差真实客观地反映出来，非常方便指导施工方合理调整尺寸。仍以导管架结构形式为例，如图2所示，每个节点的偏差值都是相对于理论数据模型的。要调整某点的三维空间位置，只需要向相反方向调整相应的偏差值就可以了。由于是在最小二乘法的基础上，所以调整的总量是最小。

图2　钢结构三维偏差示意

2.1钢结构坐标拟合原理

在海洋钢结构实际误差分析中，二维坐标拟合最为普遍和实用，现以二维平面结构为例介绍其拟合原理。首先在CAD中画出钢结构的理论模型，得到各个节点的理论坐标。为方便分析，在CAD中使理论模型的主轴线平行于X轴或Y轴，设各个节点理论坐标为（xSi，ySi），i=1，2，…，n，施工现场用全站仪测量钢结构各个节点的实际坐标，设各个实测点坐标为（xi，yi），i=1，2，…，n，根据坐标旋转平移原理，实测点通过坐标旋转平移后与理论坐标的偏差为vx、vy，则坐标变换的矩阵形式为：

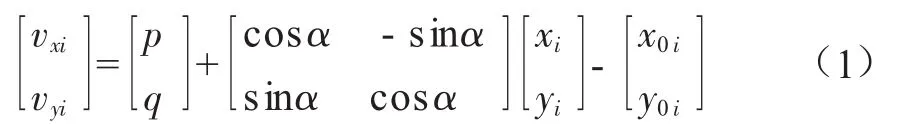
式中：vxi、vyi为第i点坐标的偏差值；α为实测坐标绕Z轴逆时针旋转的角度，p、q为X轴方向与Y轴方向的平移分量；x0i、y0i为第i点的坐标初始值。

设cosα=u，sinα=w，则（1）式可以展开为：

在平差计算前，需要计算参数p、q、u、w的初始值，设初始值为p0、q0、u0、w0，为计算参数初值，选择任意相对应的两组实测点与理论点坐标，设两组实测点坐标为xk、yk、xl、yl，两组理论点坐标为xSk、ySk、xSl、ySl，则存在如下变换关系：

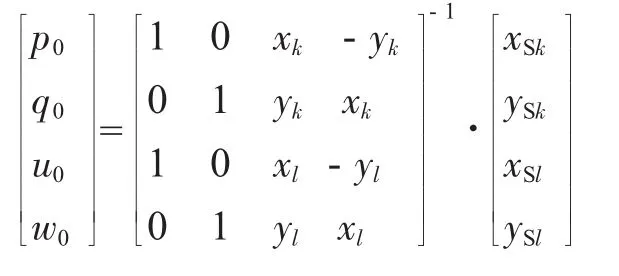
由此可计算初值p0、q0、u0、w0。

根据最小二乘法原则，应使实测坐标变换后与理论坐标的所有坐标偏差值之和为最小，即令γ=最小，同时满足条件：u2+w2=1，运用带约束条件的间接平差即可计算修正值pˆ、qˆ、uˆ、wˆ［1］，平差值为修正值与初始值之和，即

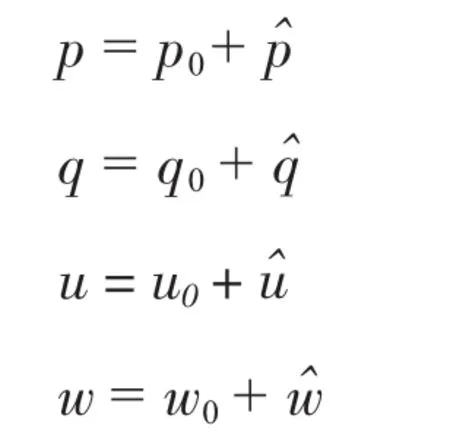
至此，坐标变换的参数计算完毕，再根据（2）式即可计算出各个节点的偏差值。

2.2程序编写

根据上述数学计算原理，利用Auto CAD VBA （VisualBasic ForApplications）编写计算程序，VBA是微软开发出来在其桌面应用程序中执行通用的自动化任务的编程语言。VBA是Visual Basic的一个子集，VBA不同于VB，主要是VBA要求有一个宿主应用程序才能运行，而且不能用于创建独立应用程序。VBA可使常用的过程或者进程自动化，可以创建自定义的解决方案，最适用于定制已有的桌面应用程序［2］。

对于本文坐标拟合程序，VBA比其他计算机语言编写的独立应用程序更具优越性，可以省略数据的输入，用鼠标点击各个节点代替数据的输入，操作非常方便，执行效率非常高。本程序运行界面如图3所示。

图3　坐标拟合程序界面

3 实际应用

在组块海上安装前，运用该方法进行模拟对接，分析计算各个对接点的偏差值，从而对过渡段或钢桩进行相应的微量调整，进而降低海上安装的风险。以垦利10-1 CEP平台为例，该项目组块共有8条腿，A轴与B轴的跨距达40 m，质量约12 000 t，由于采用浮托法安装，导管架顶部的横向无拉筋连接，导管架在运输与安装过程中顶部容易产生形变，因此安装前对对接处进行精度评定和调整非常重要。

首先，在组块陆地建造完工后测量组块底部各个立柱的圆周上若干点坐标，如图4所示，并运用文献［3］或［4］中的最小二乘法计算组块8根立柱的圆心坐标，此8个圆心坐标作为坐标拟合的设计数据使用。为方便后期偏差分析计算，在测量时使全站仪的X轴平行于组块的主轴线，组块立柱底部圆心坐标数据见表1。在海上安装组块前，测量导管架上与钢桩连接的LMU圆周上若干点坐标，依旧运用文献［3］或［4］的方法计算各个LUM最佳圆心坐标，LMU圆心坐标数据见表2。

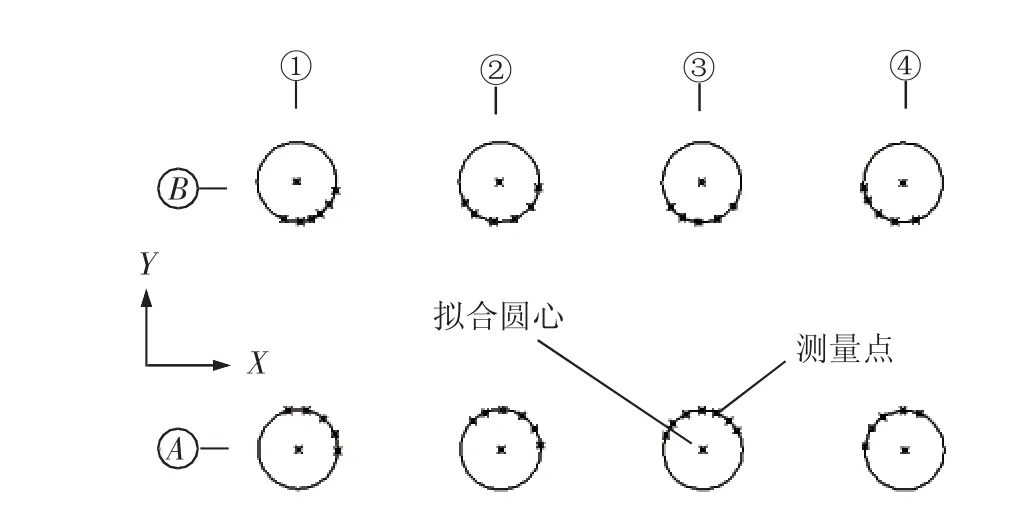
图4　组块底部立柱圆心位置

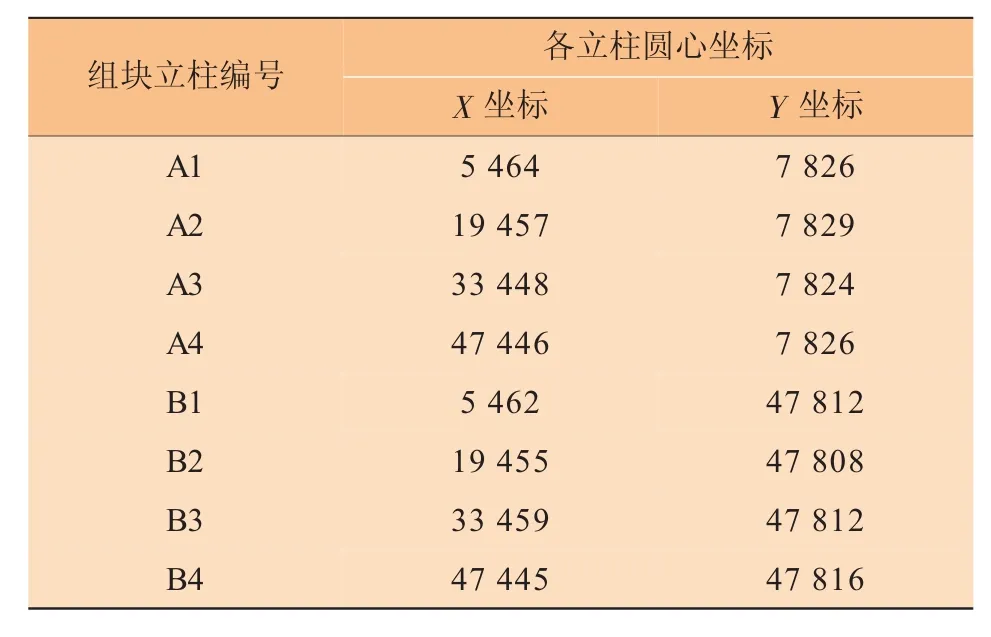
表1　组块立柱圆心数据/mm

运用本文坐标拟合方法，使实测8个LMU圆心数据最佳匹配组块底部8根立柱圆心数据。计算结果如表3所示。

依据表3的偏差值画出LMU的偏差图，如图5所示。根据该项目对接允许误差，可以首先评估安装对接的风险，进而对相应的LMU进行相应的微量调整。

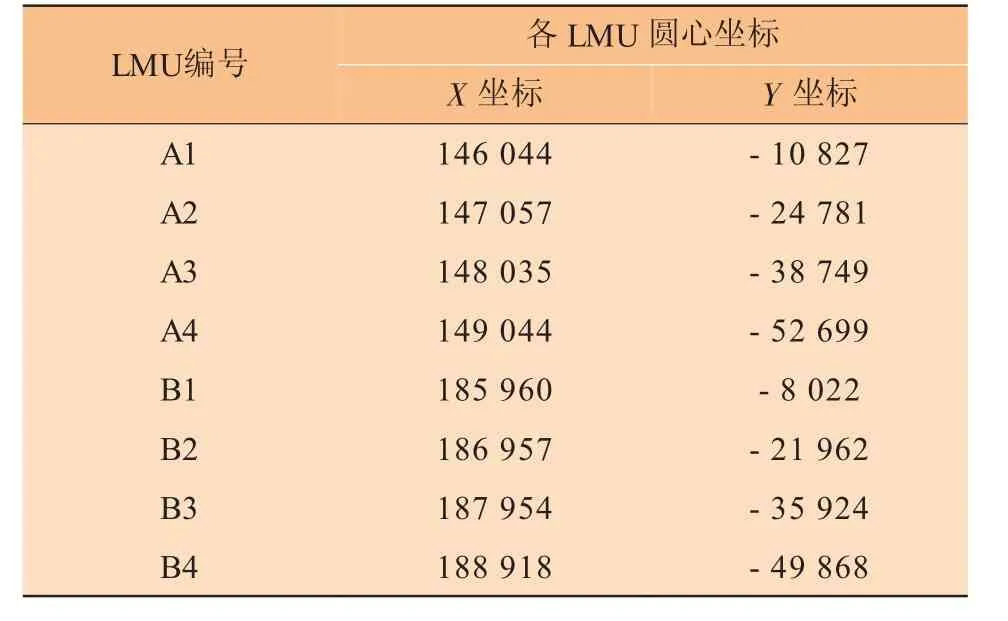
表2　L MU圆心数据/mm

表3　坐标拟合数据与偏差值/mm

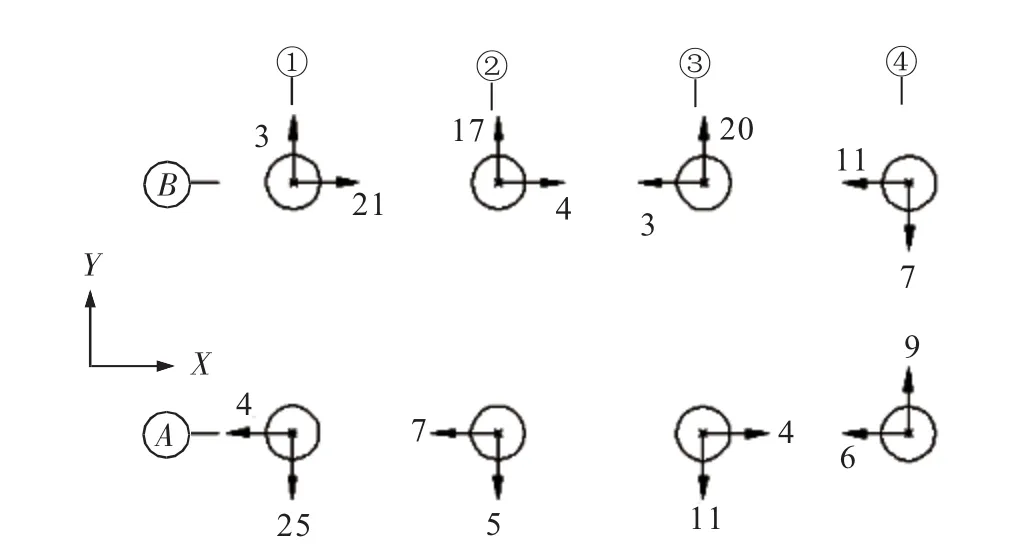
图5　垦利10-1平台L MU偏差数据

通过应用本文介绍的方法，对相应的LMU做了调整，保证了垦利10-1 CEP平台的顺利安装。相比类似项目，该项目节省至少3 d工期。

4 结束语

通过对传统的海洋钢结构误差分析方法和本文提出的海洋钢结构误差分析方法的对比，可以得出：

（1）本文钢结构误差分析法以偏差大小和方向表示，比传统的以尺寸长度表示法更加直观合理。

（2）运用最小二乘法使实测数据与设计数据进行最佳匹配，保证了所有偏差之和最小，因此可以大大减少在建钢结构修改的尺寸幅度，有效地指导施工部门对尺寸进行调整，进而缩短钢结构建造工期。

（3）对于海洋钢结构对接安装前风险评估和微量调整具有重要作用，例如以组块底部立柱的实测圆心坐标为设计数据，以钢桩、过渡段、LMU等与组块连接的结构圆心为实测数据进行数据最优匹配。从而可以直观地分析各个对接点的偏差大小和方向，如果偏差超出允许范围，可以在组块安装前对钢桩、过渡段、LMU等进行微量调整以保证顺利安装。

［1］陶本藻，邱卫宁，黄加纳.误差理论与测量平差基础［M］.武汉：武汉大学出版社，2003：102-148.

［2］张士舰，刘春杰.导管架钢桩跨距精确测量的一种新方法［J］.中国海上油气，2014，26（5）：92-95.

［3］刘春杰，张士舰.一种导管架整体尺寸检测方法［J］.测绘工程，2014，23（2）：39-44.

［4］刘春杰，张士舰，孙云虎.三维坐标系下检测导管架圆形杆件空间位置状态的方法：中国，ZL201010115279.X［P］.2012-11-28.

ANew Method for Analyzing Dimension Deviations ofOffshore SteelStructures

MENG Linghe，QIN Ye，WANG Jianxi，WANG Zhihong，WANG Xuelian
China Offshore OilEngineering Co.，Ltd.，Tianjin 300452，China

The precision is one of the important indexes in steel structure construction.Traditional analytical method to reflect precision of offshore steel structure is to compare deviations between real measured dimension data and theoretical dimension data.This method is simple but cannot directly demonstrate the deviations and is inconvenient for construction team to adjust the dimensions.In this paper，a coordinate fitting technique with least square method is applied to optimally fit measured data with design data，and the dimension deviations of steel structure are shown in 3D sizes and directions，which is direct and reasonable.The calculation method is programed with AutoCAD VBAto rapidly calculate the deviations. Keywords：least square method；coordinate fitting；design data；measured data；three dimensionalprecisions

10.3969/j.issn.1001-2206.2016.04.020

孟令河（1982-），男，山东滨州人，工程师，2007年毕业于中国石油大学（华东）测绘工程专业，主要从事钢结构测量技术研究工作。Email：306119898@qq.com

2016-01-15；

2016-04-08