基于改进EEMD和HMM的采煤机摇臂轴承故障诊断
2016-09-20王行刚
王行刚
(江苏联合职业技术学院 徐州医药分院, 江苏 徐州 221116)
基于改进EEMD和HMM的采煤机摇臂轴承故障诊断
王行刚
(江苏联合职业技术学院 徐州医药分院, 江苏 徐州221116)
提出一种基于改进集成经验模态分解与隐马尔科夫模型的采煤机摇臂轴承故障诊断方法,利用基于极值点对称延拓和余弦窗函数的改进方法,减少端点效应对分解结果的影响,从而提高了信号分解的精度;然后提取每层本征模态函数的能量熵作为隐马尔科夫模型的输入特征向量,进行故障模式识别。实验结果表明,该方法对轴承故障类型的识别率达90%以上,实现了采煤机摇臂轴承故障的准确诊断。
采煤机摇臂; 轴承; 故障诊断; 集成经验模态分解; 隐马尔科夫模型
网络出版地址:http://www.cnki.net/kcms/detail/32.1627.TP.20160902.1014.011.html
0 引言
由于煤矿井下工况条件恶劣,使得采煤机摇臂在工作时易出现较大的载荷波动,很大程度上导致了采煤机摇臂轴承故障的发生,容易造成采煤机停机,严重影响煤矿安全生产及生产效率[1]。因此,对采煤机摇臂轴承进行故障诊断分析,在故障早期分析摇臂状态并判断故障类型,具有重要的工程意义。
EMD(EmpiricalModeDecomposition, 经验模态分解)是一种自适应信号处理方法,对于非稳定性和非线性的信号分析而言,是一种较好的解决手段,因此在机械故障诊断方面得到广泛应用。在实际应用中发现,EMD分解信号过程中存在模态混叠现象和端点效应,这在很大程度上降低了信号分解的精度。EEMD(EnsembleEmpiricalModeDecomposition, 集成经验模态分解)是由Huang等[2]在EMD的基础上提出的一种新型信号处理方法,该方法克服了EMD分解的模态混合问题,但只是部分抑制了端点效应。本文提出基于改进EEMD和HMM(HiddenMarkovModel, 隐马尔科夫模型)的采煤机摇臂轴承故障诊断方法,利用基于极值点对称延拓和余弦窗函数的改进方法,减少端点效应对分解结果的影响,有效地提取出轴承的能量熵特征信息[4],然后结合具有较强分类能力的HMM,对故障类型进行诊断识别,实现采煤机摇臂轴承的故障诊断,判断摇臂工作状态[5]。
1 故障诊断关键技术
1.1EEMD理论
1.1.1EEMD算法
EEMD算法根据信号本身的信息对信号进行自适应性分解,得到一组从高频到低频的IMF(IntrinsicModeFunction, 固有模态函数)之和,使得信号分解具有一定的连贯性,以便有效地提取信号特征[2]。当轴承发生各种故障时,信号在不同频带的能量会出现不同程度的变化。因此,可以通过计算每层IMF的能量熵来提取信号的敏感特征信息,从而判断是否发生故障并识别故障类型。EEMD克服了EMD分解的模态混叠现象,但只是部分抑制了端点效应。
1.1.2端点效应抑制方法
对信号进行加余弦窗函数处理,相当于一种加权处理,根据加权效果可以抑制函数两端的信号,防止信号分解误差由两端向中心扩散,使得上、下包络线能够更好地拟合;截取信号必然发生信号的丢失,但余弦窗函数是一个无限长的函数,所以它既具有很高的分辨力,又能很好地防止信息丢失。但加窗后原信号的包络线被改变,从而导致原信号被改变[3]。针对该问题,本文研究了基于极值点对称延拓和余弦窗函数的改进算法,在对信号进行EEMD分解前先对原信号进行延拓,然后对延拓部分的信号进行加余弦窗函数处理,这样既解决了延拓过程本身带来的不确定性,又抑制了端点效应影响,提高了信号的分解精度,算法大致步骤如下。
(1) 极值点对称延拓法是一种对信号两端极值进行延拓的方法,延拓速度快。对长度为N的原始信号x(i)极值点进行延拓,极大值为s(i),i=1,2,…,m;极小值为l(j),j=1,2,…,n,然后判断是否将左右端点x(1)和x(N)作为极值点进行延拓:
(1)
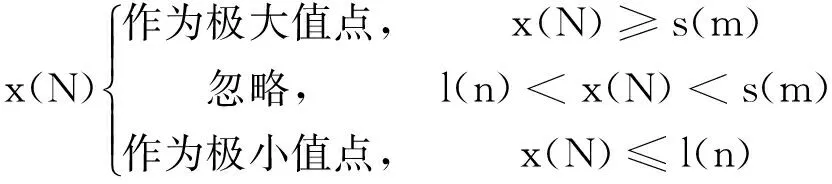
(2)
(2) 对延拓信号加余弦窗,余弦窗的窗体形状如图1所示,函数表达式为
(3)
式中:t为时间;T为余弦窗的总时间段长度。

图1 余弦窗函数
(3) 对加窗后的信号进行EEMD分解,去除分解后信号的延拓部分,得到与原始信号长度一样的信号分解结果。
1.2HMM模型
HMM模型是在Markov链的基础上发展起来的,一个HMM模型λ可由3个基本元素组成,λ=(A,B,α),其中A为隐状态转移概率分布矩阵;B为观测值概率矩阵[5];α为模型的初始概率分布向量,定义了模型初始时刻处于各个隐状态的概率分布。
随着HMM被广泛应用在实际工程问题上,逐渐形成三大经典算法[6]:① 估计。给定观察序列和模型,估测观察序列出现的概率。通常由前向-后向算法解决。② 解码。给定观察序列和模型,求可能性最大的隐藏状态序列。③ 学习。给定观察序列,通过调整HMM模型参数,使这个观察序列出现的概率最大。
在轴承故障诊断过程中,利用改进EEMD方法提取采煤机摇臂轴承振动信号敏感特征集。训练阶段,结合Baum-Welch算法,对初始化设置的HMM模型进行训练,建立各类轴承的HMM参数模型;识别阶段,利用Viterbi算法近似计算推理概率,在已知模型下,输出概率值最大的样本故障类型即为对应模型的类型。
2 实验装置及信号采集
利用采煤机摇臂加载实验台(图2)对轴承故障诊断方法进行分析验证,考虑到实验中传感器的轴向和径向安装对轴承损伤的敏感程度不同,特采用三轴加速度振动传感器对轴承振动信号进行采集,采集部位是采煤机摇臂低速轴区。通过对摇臂内轴承进行更换,模拟出正常轴承、内圈点蚀故障、外圈点蚀故障以及滚动体点蚀故障。

图2 采煤机摇臂加载实验台
对3个方向的信号进行分析可知,相对于轴向Z和切向Y来说,径向X采集到的故障轴承信号的峭度值更大,信号中含有更多的冲击成分,因此,选择径向X方向采集到的信号作为研究对象,如图3所示。该振动信号没有表现出明显的规律,所以无法准确区分故障类型。每组轴承类型采集100组数据样本,采样频率为10kHz。
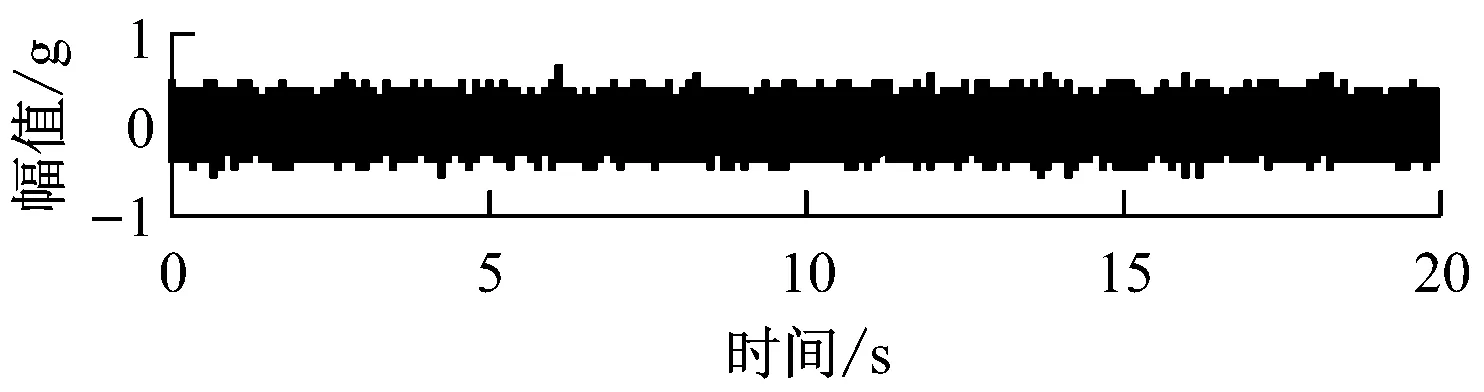
(a) 正常状态

(b) 内圈点蚀故障
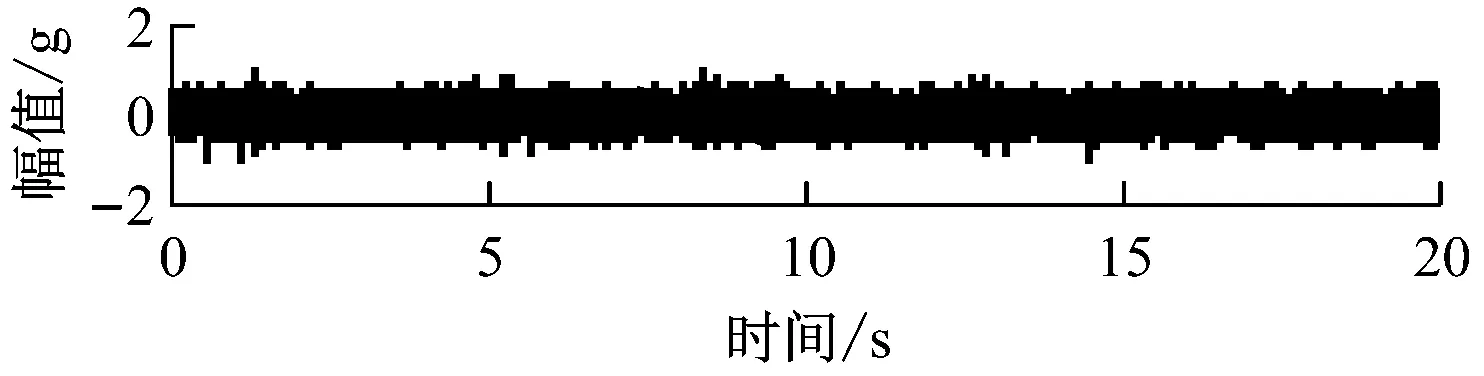
(c) 外圈点蚀故障
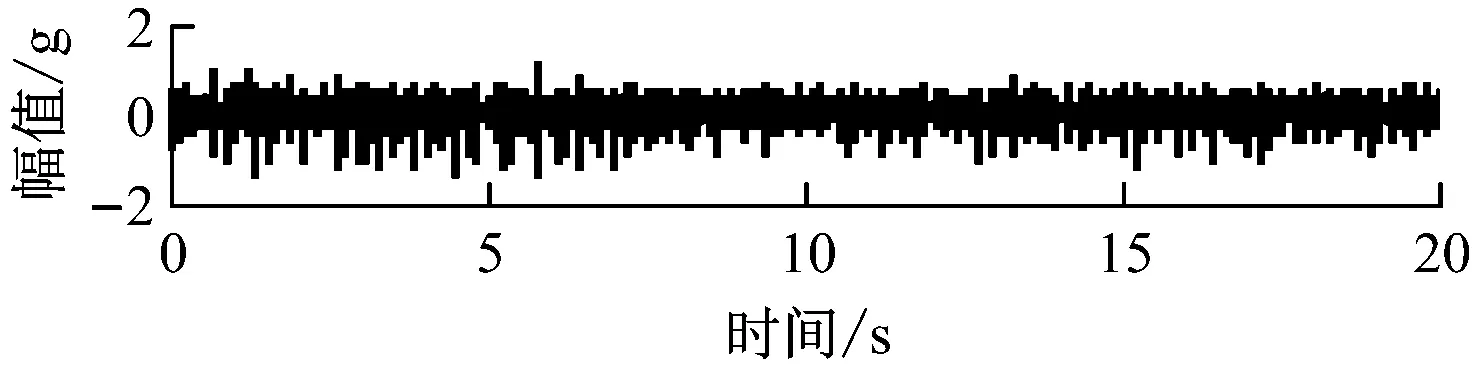
(d) 滚动体点蚀故障
3 轴承振动信号分析
用基于改进EEMD和HMM的采煤机摇臂轴承故障诊断方法对采集到的4种类型轴承信号进行分析,诊断流程如图4所示。

图4 故障诊断流程
首先对采集到的信号两端采取极值点对称延拓,然后对延拓后的信号加余弦窗函数处理,最后进行EEMD分解,设置分解过程添加的高斯白噪声幅度为0.01,循环次数为100。以内圈点蚀故障信号为例进行分析说明,分解后共得到11个IMF和余量r,前8个IMF如图5所示。


图5 内圈点蚀故障信号延拓加窗后的EEMD分解结果
去除经EEMD处理得到的每个IMF的延拓部分,得到与原信号序列长度相等的一组IMF,结果如图6所示。
对4种不同轴承类型信号进行上述分解,并对得到的一系列IMF分量分别求取能量熵,然后进行归一化处理。经分析,前8个IMF分量包含的能量超过了总能量的97%,因此,以EEMD分解得到的前8个分量的能量熵作为故障敏感集。4种轴承类型信号的前8个分量的能量熵占总能量比重如图7所示。
从图7可以大致看出每种类型轴承前8个IMF分量能量熵的变化规律,但是无法准确识别出故障类型。下面利用HMM对轴承故障类型进行诊断分类,将每种类型各80组样本的前8个IMF能量熵作为模型的输入向量,训练识别模型,建立正常轴承、内圈故障、外圈故障及滚动体故障的4种HMM状态识别模型,选取终止迭代次数为50,收敛误差为1×10-4。在实验中,初始状态概率分布向量α=[1 0 0 0],状态转移概率矩阵对模型训练的影响非常小,一般常采用左-右模式同等概率状态转移概率模型,可得状态转移概率矩阵A为



图6 内圈点蚀故障信号去延拓部分的EEMD分解结果

图7 前8个IMF分量的能量熵占总能量比重
4种类型轴承的HMM训练曲线如图8所示。利用训练好的HMM状态识别模型对剩下的4种类型轴承共80组样本进行识别分类,得到各状态的输出概率。如果样本在某个模型下的对数似然概率值最大,就表明该样本类型是这个模型所对应的故障类型。表1列出了各状态测试样本采用HMM状态识别模型识别的正确率统计结果。

图8 HMM识别模型训练曲线
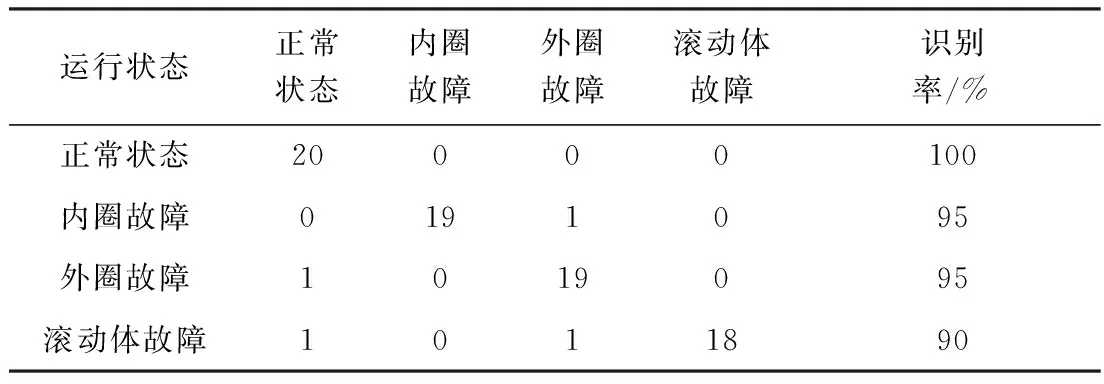
运行状态正常状态内圈故障外圈故障滚动体故障识别率/%正常状态20000100内圈故障0191095外圈故障1019095滚动体故障1011890
由表1可知,训练好的HMM状态识别模型对于正常轴承、内圈故障、外圈故障以及滚动体故障的识别率高达90%以上。
4 结语
提出了基于改进EEMD和HMM的轴承故障诊断方法,抑制了端点效应对分解结果的干扰,有效地提取出了信号的能量熵特征信息,并选择前8个IMF分量能量熵作为故障敏感集,结合HMM分类器对轴承类型进行识别分类。实验结果表明,该方法对4种状态类型的轴承故障识别率达90%以上,实现了采煤机摇臂轴承故障的准确诊断。
[1]普亚松,郭德伟,张文斌.故障诊断技术在煤矿机械设备中的应用[J].工矿自动化,2015,41(4):36-39.
[2]董文智,张超.基于EEMD分解和奇异值差分谱理论的轴承故障诊断研究[J].机械强度,2012,34(2):183-189.
[3]徐力彬,宋余庆,刘毅.基于镜像延拓和窗函数的端点效应抑制方法[J].计算机工程,2015,41(4):112-116.
[4]冯东华,贾海龙.基于EMD能谱熵和概率神经网络的采煤机摇臂齿轮故障诊断[J].煤矿机械,2014,35(7):276-278.
[5]孟宗,闫晓丽,王亚超.基于LMD和HMM的旋转机械故障诊断[J].中国机械工程,2014,25(21):2942-2946.
[6]李志农,蒋静,唐高松,等.旋转机械故障诊断中的EMD-HMM识别方法研究[J].矿山机械,2007,35(12):117-120.
Fault diagnosis of shearer rocker bearing based on improved EEMD and HMM
WANG Xinggang
(PharmaceuticalVocationalCollege,JiangsuUnionTechnicalInstitute,Xuzhou221116,China)
ThepaperproposedafaultdiagnosismethodofshearerrockerbearingbasedonimprovedEEMDandHMM.Themethodusesimprovedextremepointssymmetricextensionandcosinewindowfunctiontoreduceimpactofendeffectondecompositionresults,soastoimprovesignaldecompositionprecision;thenextractesenergyentropyofeachintrinsicmodefunctionasinputfeaturevectorofHMMforfaultpatternrecognition.Theexperimentalresultsshowthatbearingfaultidentificationrateoftheproposedmethodisabove90%,whichindicatesthemethodachievesaccuratefaultdiagnosisofshearerrockerbearing.
shearerrocker;bearing;faultdiagnosis;ensembleempiricalmodedecomposition;hiddenMarkovmodel
1671-251X(2016)09-0048-04DOI:10.13272/j.issn.1671-251x.2016.09.011
2015-09-28;
2016-07-12;责任编辑:胡娴。
国家高技术研究发展计划(863计划)资助项目(2012AA06A406)。
王行刚(1968-),男,江苏徐州人,副教授,博士,主要研究方向为药物制剂设备与技术,E-mail:2673408495@qq.com。
TD421.6
A网络出版时间:2016-09-02 10:14
王行刚.基于改进EEMD和HMM的采煤机摇臂轴承故障诊断[J].工矿自动化,2016,42(9):48-51.
