一类爱情模型的混沌同步问题

李华

（郑州航空工业管理学院　法学院，郑州450015）

一类爱情模型的混沌同步问题

李华

（郑州航空工业管理学院法学院，郑州450015）

研究了一类具有外加激励的罗密欧、朱丽叶和基内维娅之间三角恋系统的混沌同步问题，并基于Lyapunov稳定性理论得到了驱动系统与其响应系统取得混沌同步的充分条件。

三角恋；动力学模型；混沌同步

Sprott［1］提出了关于爱情的数学模型。此后，Orsucci［2］和Larsen等［3］提出了关于爱情的其他模型。Sprott［4］基于特征值的方法研究了关于幸福的动力学模型，并利用该模型建立了幸福的动力学方程。孙玉霞等［5］通过Routh-Hurwitz判据对受驱动的非线性幸福模型的动力学行为进行了解析。顾仁财等［6］研究了非线性三角恋模型及其在高斯白噪声激励下的基本动力学特征。以上研究都没有考虑外加激励的影响，事实上，当遇到外来事件的激励时，一个人的情绪就会发生变化，并产生多种反应（即超混沌现象）。在本文中，笔者研究了一类具有外加激励的三角恋模型的混沌同步问题，并基于Lyapunov稳定性理论，得到了驱动系统与其响应系统取得同步的充分条件。

1　主要结果

Strogatz研究了罗密欧和朱丽叶之间的爱情，并建立了如下关于爱情的系统：

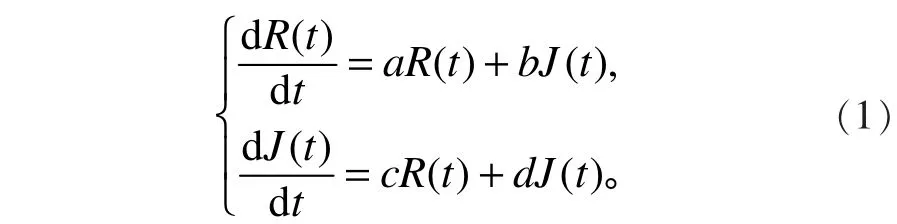
其中：R>0时，R( t)表示罗密欧（Romeo）对朱丽叶（Julie）的爱；R( t)<0时，R( t )表示罗密欧对朱丽叶的恨。J( t)>0时，J( t )表示朱丽叶对罗密欧的爱；J( t)<0时，J( t)表示朱丽叶对罗密欧的恨。

令x1( t)=R( t)，x2( t)=J( t)，则有，于是上述系统可以改写为

在系统（2）中，Strogatz没有考虑外加激励的影响，因此，如果考虑外加激励的影响，系统的响应系统为

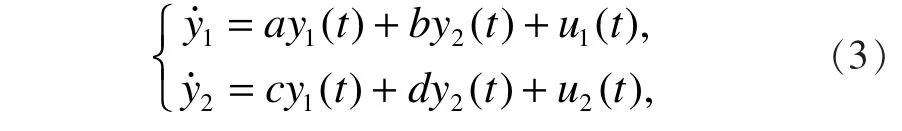
其中，u1（x）和u2（x）是外加激励。

定义系统误差e1( t)=y1( t)−x1( t )，e2(t)=y2(t) −x2( t)，式（2）与式（1）相减，得到误差系统为

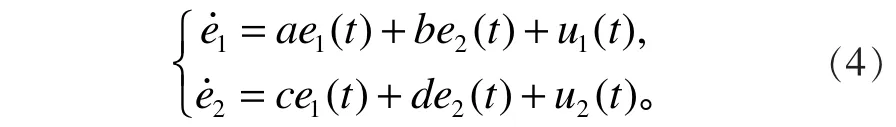
定理1：若控制器设计为u1( t)=−ae1( t)−be2( t )−e1( t)，u2(t)=−ce1( t)−de2( t)−e2( t )，则系统（2）与系统（3）能取得混沌同步。

根据Lyapunov稳定性理论，很容易证明系统（2）与系统（3）能取得混沌同步。

在Srogatz的研究基础上，Sprott将两人的爱情关系推广到三角恋的爱情关系，并建立了如下系统：其中，RJ( t)表示罗密欧（Romeo）对朱丽叶（Julie）的爱或恨，RG(t)表示罗密欧对基内维娅（guinevere）的爱或恨。

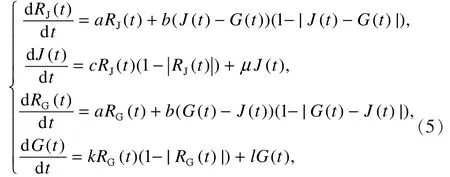
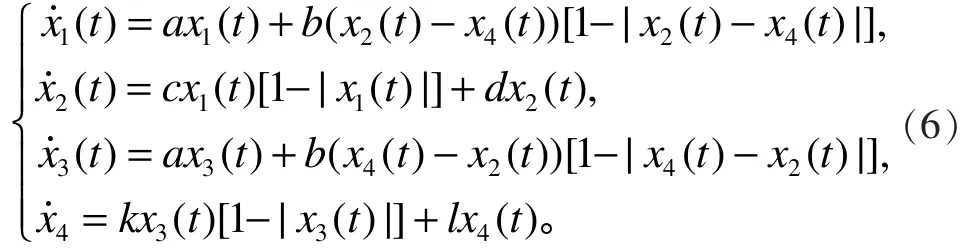
将系统（6）作为驱动系统，其响应系统为

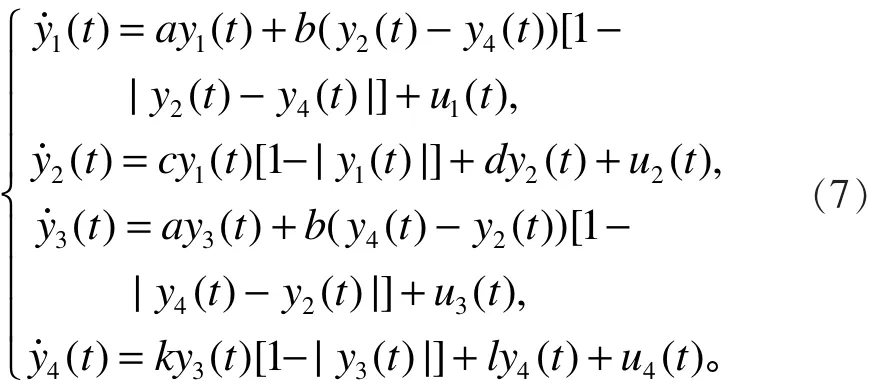
定义系统误差ei( t)=yi( t)−xi( t),(i =1,2,3,4)，式（7）与式（6）相减，得到的误差系统为

定理2：若控制器设计为u1( t)=−ae1( t)−b( y2(t ) −y4( t))[1−|y2( t)−y4( t)|]−e1( t)+b( x2( t)−x4( t ))[1−，|x2( t)−x4( t)|]，u2( t)=−cy1( t)[1−|y1( t)|]+cx1( t )[1−|x1( t)|]−de2( t)−e2( t), u3( t)=−ae3( t)−e3( t)−b( y4( t ) −y2( t))[1−|y4( t)−y2( t)|]+b( x4( t)−x2( t))[1−|x4( t)−x2( t )|], u4( t)=−ky3( t)[1−|y3( t)|]+kx3( t)[1−|x3( t)|]−le4( t )−e4( t),则系统（6）与系统（7）能取得混沌同步。

2　结束语

在本文中，笔者基于Lyapunov稳定性理论，研究了一类具有外加激励的三角恋模型的混沌同步问题，得到了驱动系统与其响应系统取得同步的充分条件。分数阶系统的混沌同步问题还有待做进一步的研究。

［1］SPROTT J C.Dynamical Models of Love［J］.Nonilear Dynamics，Phychology and Life Sciences，2004，8（3）: 303-313.

［2］ORSUCCI F.Happiness and Deep Ecology:On Noise，Harmony and Beauty in the Mind［J］.Nonlinear Dynamics，Psychology and Life Sciences，2001，5（1）:65-76.

［3］LARSON J，MCGRAW A P，CACIOPPO J.Can People Feel Happy and Sad at the Same Time［J］.Journal of Personality and Social Psychology，2001，8（1）:684-696.

［4］SPROTT J C.Dynamical Models of Happiness［J］.Nonlinear Dynamics，Psychology and Life Sciences，2005，9（1）:23-36.

［5］孙玉霞，乔晓华，包伯成.受驱动非线性幸福模型的动力学解析［J］.电路与系统学报，2012（1）：92-95.

［6］顾仁财，许勇，狄根虎.非线性三角恋模型及其在高斯白噪声激励下的基本动力学特征［J］.动力学与控制学报，2010（2）：142-145.

【责任编辑王云鹏】

The Problem of Chaos Synchronization of a Class of Love Models

LI Hua
（College of Law，Zhengzhou Institute of Aeronautical Industry Management，Zhengzhou 450015，China）

The chaos synchronization problem of Romeo，Julie and Guinevere's love-triangle model was studied in this paper.Based on Lyapunov stability theory，the sufficient conditions for systems to achieve chaos synchronization were obtained.

love-triangle；dynamical models；chaos synchronization

O231.2

A

2095-7726（2016）03-0013-02

2016-02-03

国家软科学研究计划项目（2010GXS5D234）；河南省科技厅软科学研究计划项目（122400420053）

李华（1977-），女，河南扶沟人，副教授，研究方向：经济法与宏观经济学。