基于新蕴涵算子的剩余格
2016-09-20程惠茹
程惠茹
(河南师范大学数学与信息科学学院,河南 新乡453007)
基于新蕴涵算子的剩余格
程惠茹
(河南师范大学数学与信息科学学院,河南新乡453007)
定义了一个新的蕴涵算子,证明了该蕴涵算子能构成剩余格和可交换剩余格,还证明了BL-代数是可交换剩余格的特殊情况。
蕴涵算子;剩余格;BL-代数
1986年,K.T.Atanassov提出了直觉模糊集(IFS)的概念,并发展了Zadeh模糊集的相关理论[1-2]。直觉模糊集的推导技巧为描述和处理事物的模糊性、系统的不确定性和鲁棒性提供了有效方法,直觉模糊蕴涵算子和剩余格理论在模糊推理中发挥着重要的作用。张建名等[3]研究了BL-代数中的广义模糊虑子。ZHU Yiquan等[4]研究了剩余格中的虑子理论。薛占熬等[5]研究了基于Lukasiewicz的直觉模糊三I蕴涵算子的RIL。YU Shan等[6]研究了广义直觉模糊函数的不定积分。徐泽水[7]给出了决策度量中直觉模糊数的排序方法,并研究了区间直觉模糊信息的集成方法和它在决策中的应用。周晓辉等[8]研究了三角模糊数直觉模糊Bonferroni平均算子及其应用。秦华妮等[9]对直觉模糊集的结构化进行了分析。B.Davvaz等[10]对粗糙直觉模糊信息系统进行了研究。A.Saha等[11]研究了软区间值直觉模糊粗糙集。K.V.Thomas等[12]研究了格上的粗糙直觉模糊集。GONG Zengtai等[13]研究了变精度直觉模糊粗糙集模型及应用。在此基础上,笔者定义了一个新的蕴涵算子,证明了该蕴涵算子既可以构成剩余格,又可以构成可交换剩余格,并证明BL-代数是可交换剩余格的特殊情况。
1 基础知识
定义1[1-2]:设U是一个非空论域,U上的直觉模糊集A定义为,其中,µA(x): U→[0,1]和νA(x): U →[0,1]分别表示A的隶属函数和非隶属函数,且对于任意的x∈ U,有
定义2[1-2]:设A和B为直觉模糊集,对于x∈U,记,这两个直觉模糊集的包含关系、等价关系定义为如下形式:1)A⊆B,并且µA(x)≤µB(x),νB(x)≤νA(x);2)A= B,并且µA(x)=µB(x),νA(x)=νB(x)。
定义3[1-2]:设A和B为直觉模糊集,对于x∈U,记这两个直觉模糊集的交、并和补运算定义为如下形式:1)2)
2 基于新蕴涵算子的剩余格
蕴涵算子在模糊逻辑推理中起着关键作用,下面根据定义1、定义2和定义3构造新的蕴涵算子,并证明该蕴涵算子能构成剩余格和可交换剩余格。
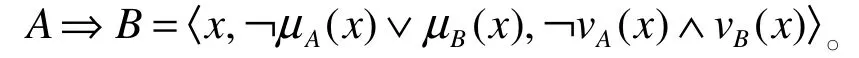
定理1:设A、B和C为直觉模糊集,若直觉模糊蕴涵⇒关于第一个变量是单调递减的,关于第二个变量是单调递增的,则有以下结论成立:
1)由A⊆B可以得出B⇒C⊆A⇒C;
2)由B⊆C可以得出A⇒B⊆A⇒C 。
证明:1)由定义2及条件A⊆B可知,µA(x )≤ µB(x),νA(x)≥νB(x)。又由定义4可知,,A⇒C=〈x,¬µA(x)。由µA(x)≤µB(x)和νA(x)≥ νB(x),有故有,则有B⇒C⊆A⇒C成立。
由定义2及条件B⊆C可知,µB(x)≤µC(x ), νB(x)≥νC(x),又由定义4可知,。由µB(x)≤µC(x ),有,又由νB(x)≥νC(x ),有,则有A⇒B⊆A⇒C成立。
定义5[14]:设P是偏序集,称P上的二元运算⊗与→为互为伴随是指以下条件成立:1)⊗:P×P→P关于两个变量都是单调递增的;2)→:P×P→P关于第一变量是不增的,关于第二变量是不减的;3)对于任意的a、b、c∈P,有a⊗b≤c当且仅当a≤b→c。
把“→”拓展到直觉模糊集上,用符号“⇒”表示,当P上的二元运算⊗与⇒互为伴随时,称(⊗,⇒)为P上的伴随对。
定义6[14]:有界格L称为可交换剩余格是指以下条件成立:1)L上有伴随对(⊗,⇒);2)是带单位元1的交换半群,其中1是L的最大元。
定理2:(RS,∩,⇒)为剩余格的充分条件是以下结论成立:1)∩是不减的,即A≤B时,有A∩C≤B∩C;2)⇒关于第二个变量是不减的,即B≤C时,有A ⇒B≤A⇒C;3)⇒关于第一个变量是不增的,即A≤B时,有B⇒C≤A⇒C;4)A∩B≤C当且仅当A≤B⇒C;5)∩满足结合率,即(A∩B)∩C=A∩(B∩C);6)∩满足交换率,即A∩B=B∩A;7)∩以1为左单位元,即1∩A=A。
证明:结论1)、结论2)和结论3)已由定理1证明,结论5)和结论6)可由定义3得出,下面仅证结论4)和结论7)。
由以上证明过程可知,A∩B≤C当且仅当A≤B⇒C,即结论4)成立。
定理3:代数结构(RS,∩,⇒)为可交换剩余格的充分必要条件是以下结论成立:1)(L,∧,∨,0,1)是有界格,相应的序为≤,0和1分别为最小元和最大元;2)(L,∧,1)是单位元为1的可交换半群;3)对于任意a、b、c∈L,a∧b≤c当且仅当a≤b⇒c。
证明:由定理2的证明过程可知,(RS,∩,⇒)是可交换剩余格。
定理4:设(L,∧,∨,⇒,⊗,0,1)是一个可交换剩余格,如果对于任意的x、y、z∈L,有A∧B=A⊗(A⇒B)和(A⇒B)∨(B⇒A)=1成立,则(L,∧,∨, ⇒,⊗,0,1)构成BL-代数。
综上所述,可知(L,∧,∨,⇒,⊗,0,1)是一个BL-代数。
在定理4中,(A⇒B)∨(B⇒A)=1称为预线性公理。
例如,闭区间[0,1]关于自然序、运算min(∧)和max(∨)、任意确定的连续t-模(⊗)及其相伴剩余蕴涵(⇒)构成一个BL-代数([0,1];min,max,⊗,⇒)。
可以验证,BL-代数是特殊的可交换剩余格。
[1]ATANASSOV K T.Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1986,20:87-96.
[2]ATANASSOV K T,GARGOV G.Interval-valued Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1989,31 (3):343-349.
[3]ZHANG J M,YANG Y.Some Types of Generalized Fuzzy Filters of BL-algebras[J].Computers and Mathematics with Applications,2008,56:1604-1616.
[4]ZHU Y Q,XU Y.On Filter Theory of Residuated Lattices [J].Information Sciences,2010,180(19):3614-3632.
[5]薛占熬,刘杰,程惠茹,等.基于Lukasiewicz的直觉模糊三I蕴涵算子的RIL[J].南京大学学报(自然科学),2015 (1):99-104.
[6]YU S,XU Z S,XU J P,et al.Indefinite Integrals of Generalized Intuitionistic Multiplicative Functions[J].Fuzzy Optimization and Decision Making,2015,14(4):459-476.
[7]徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].控制与决策,2007(2):215-219.
[8]周晓辉,姚俭,吴天魁,等.三角模糊数直觉模糊Bonferroni平均算子及其应用[J].计算机应用研究,2015(2):434-438.
[9]秦华妮,洪智勇,骆达荣.直觉模糊集的结构化分析[J].控制与决策,2015(3):561-564.
[10]DAVVAZ B,JAFARZADEH M.Rough Intuitionistic Fuzzy Information Systems[J].Fuzzy Information Engineering,2013,5(4):445-458.
[11]SAHA A,ANJAN M.Soft Interval-valued Intuitionistic Fuzzy Rough Sets[J].Annal of Fuzzy Mathematics and Information,2015,9(1):279-292.
[12]THOMAS K V,NAIR S L.Rough Intuitionistic Fuzzy Sets in a Lattice[J].International Mathematical Forum,2011,6(27):1327-1335.
[13]GONG Z T,ZHNAG X X.Variable Precision Intuitionistic Fuzzy Rough Sets Model and Its Application[J].International Journal of Machine Learning and Cybernetics,2014,5(1):263-280.
[14]王国俊.非经典逻辑与近似推理[M].北京:科学出版社,2000:26-30.
【责任编辑王云鹏】
The Residuated Lattice Based on the New Implication Operator
CHENG Huiru
(College of Mathematics and Information Science,Henan Normal University,Xinxiang 453007,China)
A new implication operator was defined in this paper.It was proved to constitute residuated lattice and the exchangeable residuated lattice.BL-algebra was proved to be a special case of the exchangeable residuated lattice.
implication operator;the residuated lattice;BL-algebra
O141.1
A
2095-7726(2016)03-0007-03
2015-12-21
程惠茹(1985-),女,河南濮阳人,硕士,研究方向:直觉模糊集。
