NSH V机动目标跟踪的自适应模型算法

聂晓华，张夫鸣，徐一鸣（南昌大学信息工程学院，江西　南昌330031）

NSH V机动目标跟踪的自适应模型算法

聂晓华，张夫鸣，徐一鸣
（南昌大学信息工程学院，江西南昌330031）

临近空间高超声速飞行器具有飞行轨迹多变、机动性强等特点，而周期性的滑跃式飞行是其常用的重要机动形式。将目标加速度建模为时间自相关的随机过程，结合“当前”统计模型的自适应跟踪思想，提出了一种针对临近空间高超声速飞行器机动目标跟踪的模型。采用容积卡尔曼滤波算法分别对单模型和交互式多模型进行了蒙特卡罗仿真分析，结果表明该模型在跟踪临近空间高超声速飞行器时有较好的跟踪精度和适用性。

目标跟踪；临近空间；自相关模型；容积卡尔曼滤波

网址：www.sys-ele.com

0 引 言

临近空间是指距地面20～100 k m的高空区域。近年来，临近空间受到了多国军事研究的高度重视，具有很强的战略意义［1］，随之出现了临近空间高超声速飞行器（near space hypersonic vehicle，NSHV）的研究热潮。NSHV由于不受轨道力学的限制，且不存在燃料消耗的问题，在高空领域有很强的应用潜力［2］。NSHV的飞行轨迹变化多样，飞行速度极快，而目前针对于NSHV的跟踪问题还没有一个很好的解决方案，对该类跟踪问题的模型算法研究具有重要的意义。

在一般的机动目标跟踪问题中，使用比较普遍的模型有匹配近匀速和近匀加速运动的匀速（constant velocity，CV）模型、匀加速（constant acceleration，CA）模型，及匀速率圆周运动的协同转弯（coordinated turn，CT）模型［3］。这些模型都仅适用于目标机动性较弱的情况，有相当的局限性，为了解决目标跟踪的突发机动情况，以相关函数对加速度建模的Singer模型［4］有较好的效果。同样得以相关函数对加加速度建模的Jerk模型［5］，对加加速度进行实时估计有更好的适用性。通常来说，目标处于不同的运动方式下，需要使用不同的模型来描述，当运动方式与模型不匹配时，会导致跟踪误差的增大，交互式多模型（interacting multiple model，I M M）算法［6-7］对多个模型之间进行交互匹配能有效地减小这种误差。

在文献［8］中提出了一种针对于临近空间高超声速滑跃式机动目标的跟踪模型，称之为Sine Wave模型，以下简称为SW模型。本文首先说明了SW模型将加速度建模为时间自相关函数的必要性和合理性，并在该模型的基础上结合自适应跟踪算法的思想，对状态噪声协方差阵进行实时地估计，最后对该自适应模型算法做了一系列的仿真分析，结果表明，本文模型在跟踪临近空间高超声速目标时有较好的跟踪精度。

1 NSHV的跟踪模型

1.1 机动特性分析

NSHV的飞行轨迹与普通的弹道导弹不同，有多种发射方式，如机载发射、火箭发射和空间平台发射，可以作周期性的滑跃式飞行，能有效地躲避地面雷达的跟踪。

使用最普遍的C V模型属于白噪声模型，是一种比较理想化的模型，更切合实际的机动模型是把机动控制项作为相关噪声（有色噪声）来建模［4］。对于常用的Singer模型，将目标加速度a假设为指数自相关的零均值随机过程，加速度的相关性随着时间间隔的增加而减小。在NSHV作近似于周期性的滑跃式飞行时，各个阶段时间内加速度的相关性随着目标的机动特性一同变化，可以近似地认为也具有周期性，而Singer模型由于建模的自相关函数并不能合理地表现出目标的机动特性，将会导致跟踪精度的降低。自相关函数曲线如图1所示。

图1 加速度自相关函数对比图

当目标作近似于周期性的滑跃式飞行时，以正弦信号的自相关函数对加速度建模，加速度的相关性是一个周期变化的函数，较指数自相关函数更为合理。

1.2 SW模型

SW模型将机动目标的加速度假设为正弦信号的自相关函数，作为一个零均值的随机过程。既有

式中，σ2为目标加速度方差；ω0为目标的机动频率。

从该函数的功率谱来考虑：

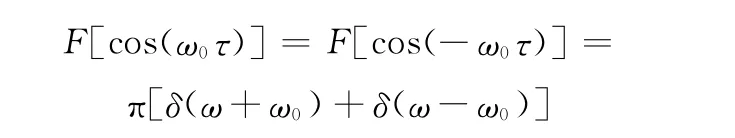
则有

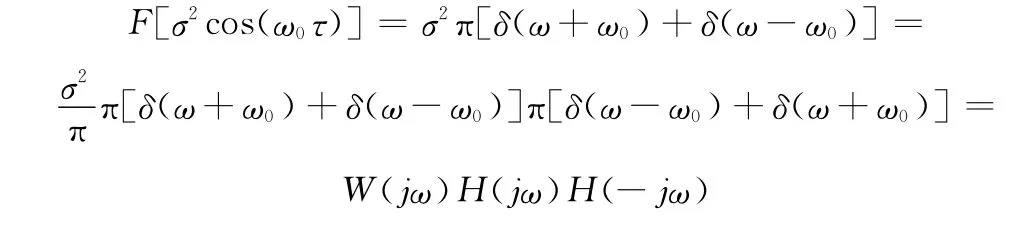
式中，W（jω）为白噪声的傅里叶变换。

利用输入为白噪声的二阶时间相关模型可以表示为

SW模型的状态方程可表示为

1.3 CS-SW模型

自适应跟踪算法指实时地估计出机动加速度或其统计特征，典型的为“当前”统计（current statistical，CS）模型自适应跟踪算法，该算法以合理的运动模型和较小的计算量而受到理论界和工程技术界的青睐［9］。其基本思想是将目标机动的变化假定为随机干扰，将机动参数的估计归结到对状态噪声协方差阵的实时估计，是一种提高目标状态估计精度的有效方法。

本文在SW模型的基础上结合CS模型的思想，采用修正的瑞利分布来描述目标机动加速度的“当前”概率分布［10］，在确定目标机动状态的同时，能够实时地估计加速度均值和状态噪声协方差阵，可以实现具有自适应跟踪效果的算法，从而达到提高跟踪精度的目的。

一般情况下可以预知目标机动加速度的最大值amax，则加速度的均值和方差表示为

当量测得到目标机动加速度的均值时，可得

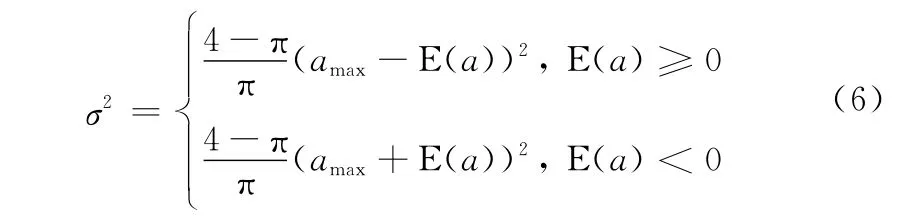
在SW模型的基础上可以得到如下关系：

对式（7）整理可写为

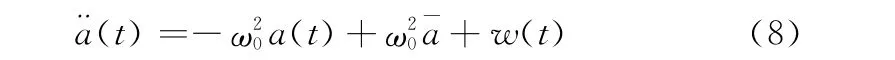
CS-S W模型的状态方程可表示为

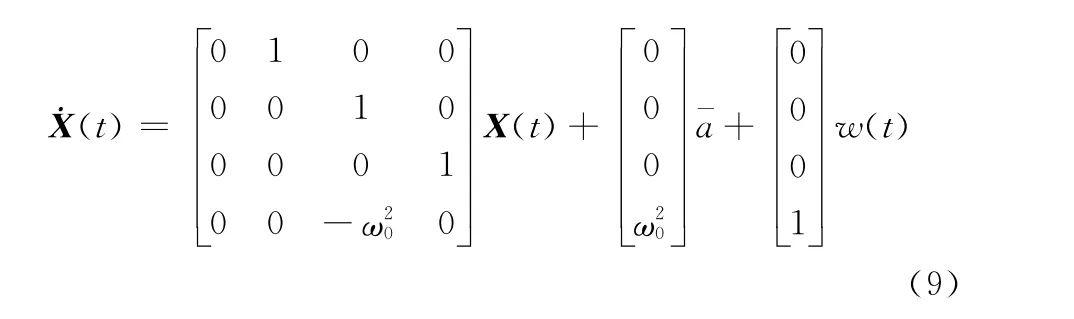
对应采样时间间隔为T的离散状态方程为

可得状态转移矩阵为

输入控制矩阵为

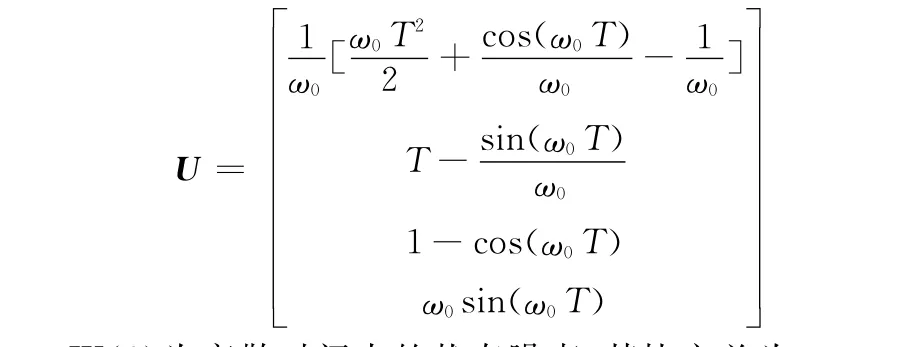
W（k）为离散时间内的状态噪声，其协方差为

1.4 量测模型

雷达的二维量测数据可表示为

式中，vk为量测噪声误差，其协方差矩阵为

且距离和方位角的误差参数［11］为

2 滤波算法

在跟踪系统中，为了方便描述，目标运动通常在直角坐标系中建模，而雷达的量测数据一般是二维的极坐标（三维时为球坐标）数据，为了解决这类的非线性跟踪问题，一般采用量测去偏转换线性化方法或者非线性滤波算法［12］。本文将采用容积卡尔曼滤波算法（cubature Kalman filter，C K F）进行仿真分析。

对于一个动态系统：

式中，X表示系统的状态量；Z表示系统的量测值；w和v分别表示系统相互独立的状态误差和量测误差；协方差矩阵为Q和R。

在非线性高斯滤波的统一框架下［13］，将直角坐标系的多维空间积分区域转换到球面径向坐标系中，利用高斯求积准则和三阶容积准则［14-15］作数值近似处理，可以得到基本CKF算法。

当状态X为n维向量时，选取2n个采样点，得到C K F的滤波步骤如下。

构造矩阵：

时间更新：

（1）选取采样点

（2）传递采样点

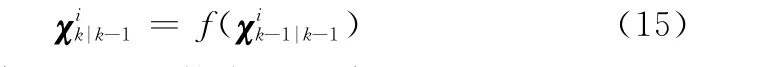
（3）预测状态量及误差协方差矩阵

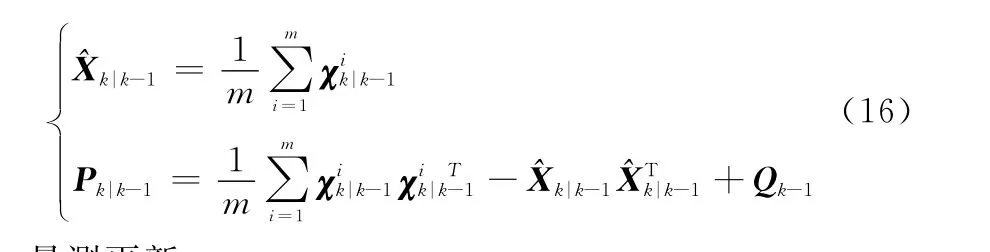
量测更新：

（1）选取采样点

（2）传递采样点

（3）预测量测值及误差协方差矩阵

（4）计算状态量与量测值的互协方差矩阵

（5）更新状态量及误差协方差矩阵

相比较于常用的无味卡尔曼滤波（unscented Kalman fliter，UKF）而言，CKF在滤波过程中不需考虑参数的选择问题，确保了采样点的权值始终为正，因此不会出现UKF在处理高维非线性系统时因参数选择不当所引起的滤波发散问题［16］。同时，对于三维以上的非线性系统，CKF比UKF有更好的估计精度和稳定性［17］，在机动目标跟踪领域中有着较为广泛的应用。

3 仿真分析

3.1 近周期性机动的仿真分析

参考已公布的美国X-51 A飞行器在2010年～2013年间4次试飞的试验数据［18-19］，基于飞行轨迹的数学模型，模拟出NSHV的近周期性飞行轨迹。

具体控制方案为：助推段，飞机将NSHV送至8 k m高度，助推器点火将NSHV推进到26 k m处；巡航段，在飞行器转入高空巡航段时，飞行器与助推器分离，分离后，让飞行器进行无动力滑翔，当飞行器下降到预定高度16 k m后，由于飞行器升阻比较大，提供的升力将使飞行器速度倾角由负变正，使轨迹拉升，与此同时超燃冲压发动机点火发动，使飞行器向上加速推进，当把飞行器推进到预定高度24 k m后，关闭超燃冲压发动机，随后飞行器又进行无动力滑翔，在高度约17 k m处，超燃冲压发动机再次点火，使飞行器加速向上推进至高度23 k m处，超燃冲压发动机关闭，飞行器再度进行无动力滑翔，重复上述过程，直至到达目的地上空；俯冲攻击端，采用比例导引法改变飞行器的飞行轨迹，通过改变弹道倾角和攻击目标视线角的关系，实现对目标的攻击。飞行轨迹示意图如图2所示。

图2 近周期性飞行轨迹示意图

使用图2中的飞行轨迹进行仿真分析，x方向的初始距离为0；y方向的初始距离为8 000 m。雷达采样时间间隔T为1 s，总采样时间为250 s。具体参数如下：

（1）SW模型：ω0为0.05，σ2为1002；

（2）CS-SW模型：ω0为0.05，am ax为5g。

进行100次蒙特卡罗仿真得到的位置均方根误差（root mean square error，R M SE）如图3所示。

图3 位置R M SE

分析图3不难发现，在近周期性机动仿真的初始阶段，CS-SW模型的跟踪误差大于SW模型，经过短时间的自适应调整过程，CS-SW模型的跟踪误差趋于稳定，比SW模型的跟踪效果更好。

3.2 非周期性机动的仿真分析

使用图4中的飞行轨迹［20］进行仿真分析，x方向的初始距离为10 000 m，初始速度为340 m/s；y方向的初始距离为10 000 m，初始速度为0 m/s。雷达采样时间间隔T 为1 s，总采样时间为450 s。

3.2.1 单模型仿真分析

分别对CS-SW和SW进行单模型仿真分析。具体参数如下：

（1）SW模型：ω0为0.05，σ2为1002；

（2）CS-SW模型：ω0为0.05，am ax为10g。

进行100次蒙特卡罗仿真得到的位置RMSE和速度RMSE分别如图5和图6所示。

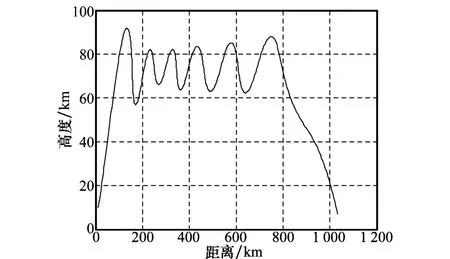
图4 非周期性飞行轨迹示意图

图5 单模型的位置RMSE

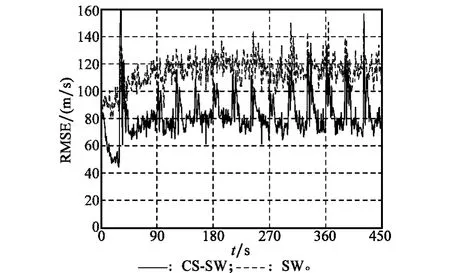
图6 单模型的速度RMSE

从图5和图6中可知，在非周期性机动仿真中，CS-SW模型和SW模型的跟踪效果均稍差于近周期性机动的跟踪效果。CS-SW模型的位置误差曲线比SW模型的稍低，且CS-S W模型的速度量跟踪效果更好。

3.2.2 多模型仿真分析

使用CV模型分别与CS-SW模型和SW模型交互，进行IMM多模型仿真分析。具体参数如下。

（1）SW模型：ω0为0.05，σ2为1002。

（2）CS-SW模型：ω0为0.05，am ax为10g。

（3）CV模型：σ2为1。

模型先验概率：u0=［0.5，0.5］。

模型转移概率：

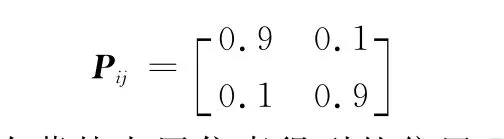
进行100次蒙特卡罗仿真得到的位置RMSE和速度RMSE分别如图7和图8所示。

图7 IMM多模型的位置RMSE

图8 IMM多模型的速度RMSE

在IMM多模型仿真中，位置误差量的对比效果与单模型仿真相同，速度误差量比单模型仿真稍小，且采用CSSW模型的IMM算法比SW模型效果更好。

4 结 论

通过对NSHV机动特性的简单分析，说明了SW模型以正弦信号的自相关函数对加速度建模的合理性，在此基础上，本文考虑到自适应跟踪算法的优势，将“当前”统计模型的思想与SW模型相结合，达到了实时估计加速度均值和状态噪声协方差阵的目的，有效地提高跟踪精度。利用已公布的试验数据模拟出NSHV近周期性的滑跃式飞行轨迹，使用CKF算法和IMM算法对本文模型进行了仿真分析，验证了本文所提模型在处理NSHV的跟踪问题时比SW模型的效果更好。

［1］Xu Y F，Jiang B，Gao Z F，et al.M odeling analysis and adaptive observer based fault diagnosis for near space vehicle［C］∥Proc. of the7th Asian Control Conference，2009：1114-1119.

［2］Wang WQ.Near space vehicle borne SAR with reflector antenna for high resolution and wide swath remote sensing［J］.IE E ETrans.on Geoscience and Remote Sensing，2012，50（2）：338-348.

［3］Li X R，Jilkov V P.Survey of maneuvering target tracking，part I：dyna micmodels［J］.IE E E Trans.on Aerospace and Electronic Systems，2003，39（4）：1333-1364.

［4］He Y，Xiu J J，Guan X，et al.Radar data processing with applications［M］.3rd ed.Beijing：Publishing House of Electronics Industry，2013：184-185.（何友，修建娟，关欣，等.雷达数据处理及应用［M］.3版.北京：电子工业出版社，2013：184-185.）

［5］Shrabani G，Siddhartha M.Tracking reentry ballistic targets using acceleration and jerk m odels［J］.IE E E Trans.on Aerospace and Electronic Systems，2011，47（1）：666-683.

［6］Chze E S，Inseok H.Algorith m for performance analysis of the I M Malgorithm［J］.IE E E Trans.on Aerospace and Electronic Systems，2011，47（2）：1114-1124.

［7］Li X R，Jilkov V P.Survey of maneuvering targettracking，part V：multiple-model methods［J］.IE E E Trans.on Aerospace and Electronic Systems，2005，41（4）：1255-1321.

［8］Wang G H，Li J J，Zhang X Y，et al.A tracking model for the near space hypersonic slippage leap maneuvering target［J］.Acta Aeronautica et Astronautica Sinica，2014，35（6）：1611-1622.（王国宏，李俊杰，张翔宇，等.临近空间高超声速滑跃式机动目标的跟踪模型［J］.航空学报，2014，35（6）：1611-1622.）

［9］Shi Z S，Liu Z.Method and theory of target tracking and data fusion［M］.Beijing：National Defense Industry Press，2010：98-99.（石章松，刘忠.目标跟踪与数据融合理论及方法［M］.北京：国防工业出版社，2010：98-99.）

［10］Zhou H R.A“current”statistical m odel and adaptive tracking algorith m for maneuvering targets［J］.Acta Aeronautica et Astronautica Sinica，1983，4（1）：73-86.（周宏仁.机动目标“当前”模型与自适应跟踪算法［J］.航空学报，1983，4（1）：73-86.）

［11］Ning X，Ye C M，Yang J，et al.Cubature Kalman filtering for orbit determination of space targets［J］.Chinese Journal of Radio Science，2014，29（1）：26-34.（宁夏，叶春茂，杨健，等.容积卡尔曼滤波在空间目标轨道确定中的应用［J］.电波科学学报，2014，29（1）：26-34.）

［12］Zhan RH，Zhang J.N onlinear filtering theory with target tracking application［M］.Beijing：National Defense Industry Press，2013：23-24.（占荣辉，张军.非线性滤波理论与目标跟踪应用［M］.北京：国防工业出版社，2013：23-24.）

［13］Simon J，Jeffrey U，Hugh F D.A new method for the nonl inear transformation of means and covariances in f i lters and estimators［J］. IEEE Trans.on Automatic Control，2000，45（3）：477-482.

［14］Ienkaran A，Sim on H.Cubature Kalman filters［J］.IE E E Trans.on Automatic Control，2009，54（6）：1254-1269.

［15］Arasaratnam I，Haykin S，H urd T R.Cubature Kalman fi ltering for continuous-discrete systems：theory and simulations［J］.IE E E Trans.on Signal Processing，2010，58（10）：4977-4993.

［16］W ang X X，Pan Q，H uang H，et al.Overview of deterministic sa m pling filtering algorith ms for nonlinear system［J］.Control and Decision，2012，27（6）：801-812.（王小旭，潘泉，黄鹤，等.非线性系统确定采样型滤波算法综述［J］.控制与决策，2012，27（6）：801-812.）

［17］Sun F，Tang L J.Estimation precision comparison of Cubature Kalman filter and Unscented Kalman filter［J］.Controland Decision，2013，28（2）：303-308.（孙枫，唐李军.Cubature卡尔曼滤波与Unscented卡尔曼滤波估计精度比较［J］.控制与决策，2013，28（2）：303-308.）

［18］Graham C，Heath J，Christopher A，et al.Analysis of modal growth on the leeward center plane of the X-51 vehicle［R］. U S A：University of Minnesota，2009.

［19］Evgeny M.Scatter pattern calculations and determination performance limitations of existing air defense systems for intercepting hypersonic vehicles［R］.U S A：Atlanta，Georgia，2012.

［20］Xiao S，Tan X S，Li Z H，et al.Tracking model based on the SC TIM M near space hypersonic target［J］.Modern Radar，2013，35 （4）：15-19.（肖松，谭贤四，李志淮，等.基于SCT-IMM的临近空间高超声速目标跟踪模型［J］.现代雷达，2013，35（4）：15-19.）

Adaptive model algorith m for maneuvering target tracking of NSH V

NIE Xiao-hua，Z H A N G Fu-ming，XU Yi-ming
（The Com munication and Engineering College Nanchang University，Nanchang 330031，China）

The near space hypersonic vehicle has the variable flight path，strong mobility and other characteristics.And the periodic ski-jum pflightisa common and important maneuverform.Modeling the target acceleration as a stochastic process with time autocorrelation，combined with adaptive tracking thinking of the“current”statistical model，a model for the near space hypersonic vehicle maneuvering target tracking is proposed. Use the cubature Kalman filter algorithm to analyze the Monte Carlo simulation of the single model and the interactive multiple model，the results show that the model for tracking the near space hypersonic vehicle has a better tracking accuracy and applicability.

target tracking；near space；autocorrelation model；cubature Kalman filter

TN953

A

10.3969/j.issn.1001-506 X.2016.03.05

1001-506 X（2016）03-0506-06

2015-02-16；

2015-06-07；网络优先出版日期：2015-09-28。

网络优先出版地址：http：//www.cnki.net/kcms/detail/11.2422.TN.20150928.1036.002.html

聂晓华（1969-），男，副教授，博士，主要研究方向为最优状态估计与系统辨识、电气信息。

E-mail：niexiaoh@163.com

张夫鸣（1993-），男，硕士研究生，主要研究方向为最优状态估计与系统辨识。

E-mail：zfm data@163.com

徐一鸣（1991-），男，硕士研究生，主要研究方向为最优状态估计、自动控制理论应用。

E-mail：604710755@qq.com