广义的Cauchy型Taylor公式中中值点的渐近性

李冬辉

(河南教育学院 数学与统计学院，郑州 450046)



广义的Cauchy型Taylor公式中中值点的渐近性

李冬辉

(河南教育学院 数学与统计学院，郑州 450046)

研究当区间长度趋于零时，广义的Cauchy型Taylor公式中中值点的渐近性。

广义的；Cauchy型Taylor公式；中值点；渐近性

0　引言

文献[1]得到了一个高阶导数形式的、广义的Cauchy型Taylor公式。本文研究该公式中中值点的渐近性质。首先，引述广义的Cauchy型Taylor公式。

定理1[1](ⅰ)若f(k)(x)(k=1,2,…,n)与g(k)(x)(k=1,2,…,m)分别在[a,b]上连续；(ⅱ)f(n+1)(x)与g(m+1)(x)在(a,b)内存在，且g(m+1)(x)≠0，则在(a,b)内至少存在一点ζ，使得下列广义的Cauchy型Taylor公式成立

其中f(0)(a)=f(a)，g(0)(a)=g(a),而ζ称为中值点。

由定理1可知，若(ⅰ)f(k)(x)(k=1,2,…,n)与g(k)(x)(k=1,2,…,m)分别在U(a)内连续；(ⅱ)f(n+1)(x)与g(m+1)(x)在U0(a)内存在，且g(m+1)(x)≠0，则∀∈U(a)，至少存在一点ζ∈(a,x)或ζ∈(x,a)，使得下列式子成立

(1)

本文研究当x→a时，ζ的变化规律.

1　主要定理

定理2若(ⅰ)f(k)(x)(k=1,2,…,n)与g(k)(x)(k=1,2,…,m)分别在U(a)内连续；

(ⅱ)f(n+1)(x)在U0(a)内存在，g(m+1)(x)在U(a)内存在，g(m+1)(x)≠0，且g(m+1)(x)在a点连续；

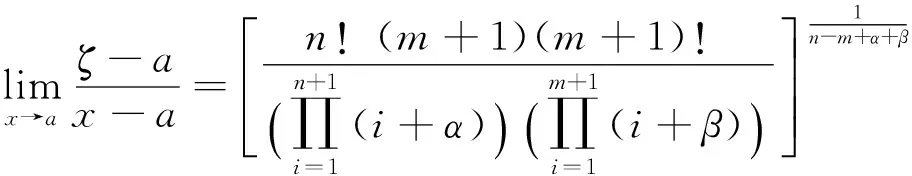
证明构造函数

连续使用n+1次L′Hospital法则可得

(2)

连续使用m+1次L′Hospital法则可得

(3)

由(2)、(3)式得

(4)

另一方面，由Taylor公式得

其中，η介于a与 之间。

由(1)式及上式得

(5)

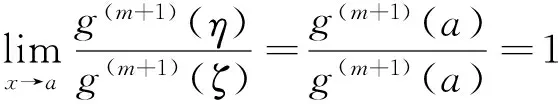
则由(5)式得

(6)

由(4)、(6)式得

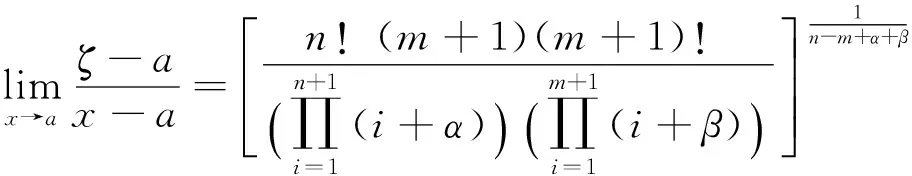
定理3若(ⅰ)f(k)(x)(k=1,2,…,n)与g(k)(x)(k=1,2,…,m)分别在U(a)内连续；

(ⅱ)f(n+1)(x)在U0(a)内存在，g(m+1)(x)在U(a)内存在，g(m+1)(x)≠0,且g(m+1)(x)在a点连续；

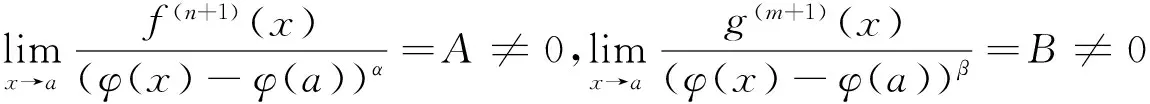
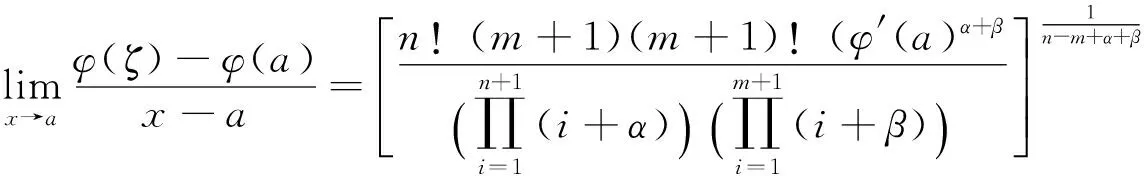
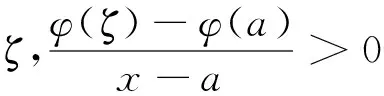
取F(x)为定理2中所设，根据定理条件，连续使用n+1次L′Hospital法则可得

(7)

连续使用m+1次L′Hospital法则可得

(8)

由(7)、(8)式得

(9)

另一方面，由定理2的证明过程可知

(10)

由(9)、(10)式得

推论在定理3的条件下，(1)式中的ζ满足

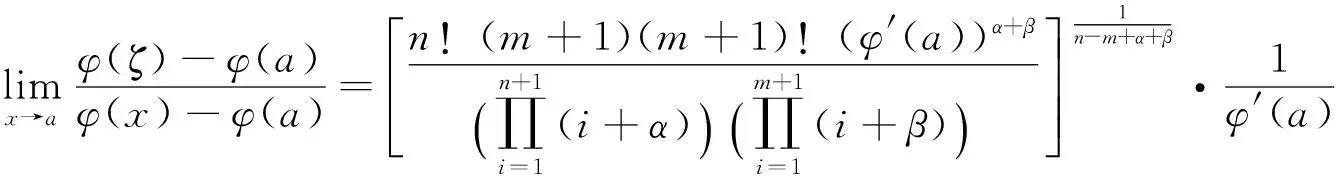
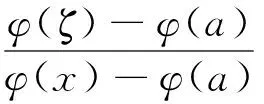
由定理3得

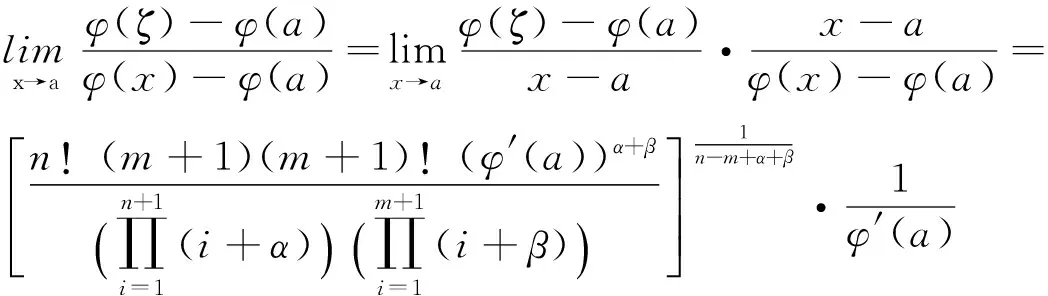
[1]苏翎，赵振华，董建.一个广义的Cauchy型的Taylor公式[J].数学的实践与认识，2009(21)：214-216.

(责任编辑赵冰)

Asymptotic properties of median point of Generalized Taylor formula of Cauchy form

LI Dong-hui

(School of Mathematics and Statistics，Henan Institnte of Education, Zhengzhou, 450046,China)

The paper studies the asymptotic properties of median point of generalized Taylor formula of Cauchy form, as interval length goes to zero.

generalized; Taylor formula of Cauchy form; median point; asymptotic properties

2016-03-05

李冬辉(1963—)，男，河南许昌人，河南教育学院数学与统计学院副教授，主要研究方向：基础数学。

10.13783/j.cnki.cnki.cn41-1275/g4.2016.04.024

O172.2

A

1008-3715(2016)04-0117-03