基于粗糙集神经网络的科技金融信用风险评价研究
2016-09-20王洁陈刚
王洁,陈刚
(1.东莞市电子计算中心,东莞 523123;2.广东理工职业学院计算机系,中山 528458)
基于粗糙集神经网络的科技金融信用风险评价研究
王洁1,陈刚2
(1.东莞市电子计算中心,东莞 523123;2.广东理工职业学院计算机系,中山 528458)
针对科技金融信用风险评价的效率低下,导致信贷审批成本过高,归其原因为科技金融服务行业针对企业信用评价模型不佳,评价指标过多,评价时间过长,导致成本过高;针对此不足,提出一种基于粗集神经网络的科技金融信用风险评价模型,该模型在不影响分类属性的原则下有效地约简企业的财务指标,同时利用BP神经网络容错能力,对信贷企业进行很好的分类,最后将该模型应用于实验,实验表明该模型有效。
科技金融;风险评价;粗糙集;神经网络
0 引言
科技和金融紧密结合是金融服务实体经济、助推经济转型升级的有效途径,是贯彻落实创新驱动发展战略的有效支撑措施。近年来随着经济不断发展,科技与金融结合也越来越活跃,而在科技金融中信用贷款业务也不断增加,然而,信贷效率却非常低,其主要原因是信贷审批手续过于烦琐,调查信贷指标过多,导致审批成本上升和审批周期过长,这些现象与活跃的信贷市场形成鲜明的对比,也困扰着大量的科技金融机构,特别对于政府性区科技金融服务机构,它们每天面临大量本地区企业信用风险评估,这些评估活动表现为量大、指标多、时间长,严重地阻碍了当地经济的快速发展。
国内已经有很多学者做了这方面研究,在科技金融信用评价方面的研究不多,如卢超等人提出商业银行对中小企业信用风险评价的方法探索,但该文仅仅从方法上对普通企业信用评价给出了指导[1];楼际通等人提出的商业银行个人信用风险评价的投影寻踪建模及其实证研究,是以数学建模为工具,从而可以对信用进行分类和量化,但问题是当指标数据太大时,显然要耗费大量的时间[2];曾诗鸿等人提出了基于KVM模型的制造业上市公司信用风险评价研究,该模型虽然针对性很强,但对于科技型的企业则有些乏力[3];这些大部分都是从普通企业指标去研究的,但是针对科技型企业研究的极少,如汪泉等提出的科技金融信用风险的识别、度量与控制[4],虽然比较详细了描述了科技金融中的企业信用评价与度量应该关注因素,同时提到一个“SPECAIL”信用评价法,但是该方法信用评价的时间过长,浪费金融服务行业机构的时间更加大了科技型企业的风险,因为科技型企业的弹性较大,在缺少资金情况下,倒闭的风险比普通企业更大,当然该类型的企业也可以在较短的时间内赢利,因此该类企业对时间的控制显得非常重要。
基于上述情况,针对于科技金融中信用风险评估过慢、准确率不高;同时科技型企业的偿债能力的弹性大等特点,本文提出了一种基于粗集神经网络的科技金融信用风险评价模型,该模型利用粗糙集的约简功能可以删除冗余数据,减少了BP神经网络的输入维,从而减少了指标数据的采集时间和减轻了工作量,更减少了BP神经网络的训练时间和分类时间,提高了科技金融服务行业信贷审批工作效率,节省了科技金融服务审批成本和科技型企业的信贷成本,为科技金融服务工作的顺利展开创造了一定的技术条件;同时由于科技型企业的偿债能力弹性大,快速获得贷款能为科技型企业的生存创造一定的条件。
1 相关理论
科技金融是以促进科技创新活动为目的,以组织运用金融资本和社会资本投入科技型企业为核心,以定向性、融资性、市场性和商业可持续性为特点的金融活动总称。
科技金融服务主要解决科技型企业贷款难,融资难的问题,引进银行、创投、担保、小额贷款、投资管理、资产评估、知识产权质押等金融和服务机构,整合与集成各相关服务功能,为企业提供促成技术交易一揽子解决方案。业务包括创业企业投资服务、企业贷款担保服务、企业投融资策划服务、小额贷款服务、企业投融资服务、下岗失业小额贷款担保、私募股权投资、大学生自主创业贷款担保、企业银行贷款担保、无抵押贷款(担保)等。因此,科技金融服务的核心是科技型企业的信用风险评估。
本文的模型是基于粗糙集和BP的神经网络网络的组合模型,在该模型中涉及到粗糙集与BP神经网络,粗糙集理论在当今的人工智能智能领域有着广泛的应用领域。本文应用了粗糙集理论在不减少依赖度的前提下对企业的冗余指标进行删除,从而减少了财务指标的采集时间,减少了BP神经网络的输入维,减少BP神经网络的训练时间和分类时间,进一步缩短了信贷系统的审批时间,节约了信贷审批成本;应用BP神经网络进行分类是因为BP网络具有较好的泛化能力和容错能力,同时利用粗糙集可以约简输入维,提高BP网络的收敛时间。
2 粗糙集的相关理论
粗糙集是由波兰科学家Z.Pawlak于1982年提出来的。粗糙集理论是继概率论、模糊集、证据理论之后又一个处理不确定性的数学工具。作为一种崭新的软计算方法,粗糙集近几年来越来越受到重视,其有效性已在金融工程、智能控制、模式识别等众多领域得到了证实,也是当今人工智能领域中的研究热点之一。同时,其在处理噪声、不确定性甚至不完整性方面也有着卓越的优势[5-7]。
(1)上近似和下近似概念 理解上近似于下近似,首先要定义知识库,令知识库K=(U,S),U,S分别表示论域及在论域上的一个等价关系簇,对于X,若∀x⊆U以及论域U上的一个等价关系R∈IND(K),则认为R的上近似与下近似分别表示为(1)(2)。
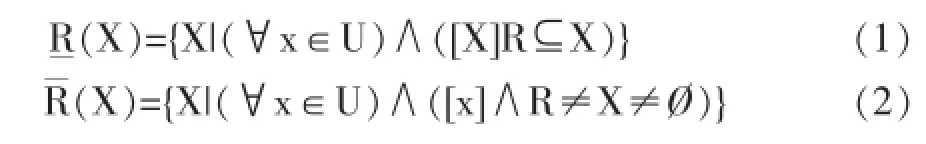
同时用bnR=R(X)-R(X)表示X对于R的边界域,定义posR(X)=R为X等价关系R的正域。定义negR(X)=U-R(X)为X对R的负域。则R=posR(X)∪bnRR(X)。
(2)知识的约简 约简是粗糙集理论应用的重要方面之一。粗糙集约简认为,属性对知识库的决策的重要程度应该不相同,有些数据甚至冗余,知识约简正是通过寻找其属性的最小依赖集,从决策表中剔除一些对决策基本没有作用的属性的过程,简称为约简。
同时若知识库中存在一个这样的等价关系R={P,Q},则认为P∩Q是等价关系上的一个不可分割的等价关系,则记IND(R),此时Q的P上近似记为:

对于给定的知识库K=(U,S)和知识库上的一组关系P⊆S,对于任意的G⊆P,若G满足以下条件:
①G是独立的,
②IND(G)=IND(P)。则称G为P的一个约简,表示为G∈RED(P),认为RED(P)为P的全体约简组成的集合。
(3)知识的依赖度 已知某知识库K,若存在P且∀P,Q∈IND(K),则知识依赖度的定义为公式为:
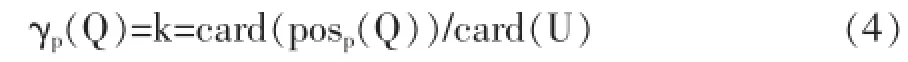
其中γp(Q)表示知识Q对P依赖程度,Card表示集合运行中的基数运算符,若γp(Q)为1,则认为Q完全依赖于P;若γp(Q)介于(0,1)时,则认为Q部分依赖于P,且Q中有部分是由P导出的;若γp(Q)为0,则认为Q与P完全没有关系,表示P的任何变化都对Q无影响。
(4)知识的重要度 知识重要度是表示某个知识库中某个属性对于整个知识系统的重要程度的一个维度,对于知识系统中的所有属性,若去除一些属性之后,若论域U的划分还和以前一样,则认为该除去的属性对于知识系统来说不重要,若除去一些属性之后,论域U的划分和去除属性前不一样,则认为该去除的属性对知识比较重要,若知识系统IS={U,Q,V,f}且∀P⊆Q,以及α∈P,则知识系统中表示重要度的公司如下:
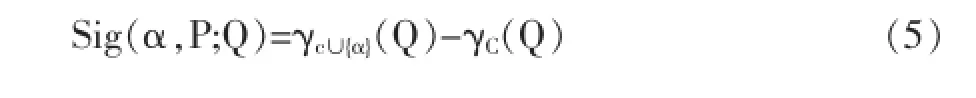
由公式(5)可以知,若是Sig越大,则说明α属性对于C的划分的影响越大,α属性对于知识系统的重要度就越大;若Sig=0,则说明α属性对C的划分没有影响,可以认为α属性对IS重要度较低。
3 神经网络理论
本文中的神经网络主要是是BP(Back Propagation)神经网络,BP是由Rumelhart和McCelland科学家于1986年提出的,是一种按误差逆向传播的算法训练的多层前馈式网络,是当今神经网络应用领域最广泛的网络模型之一[8]。BP神经网络能够自动学习和存储大量的模式映射,并且不需要事先准备描述的数学公式,就能以最速的速度进行学习,并且通过不断地调整权值和阈值来达到网络训练的要求,该神经网络模型的拓扑结构包括输入层、隐含层、输出层,如图2所示。
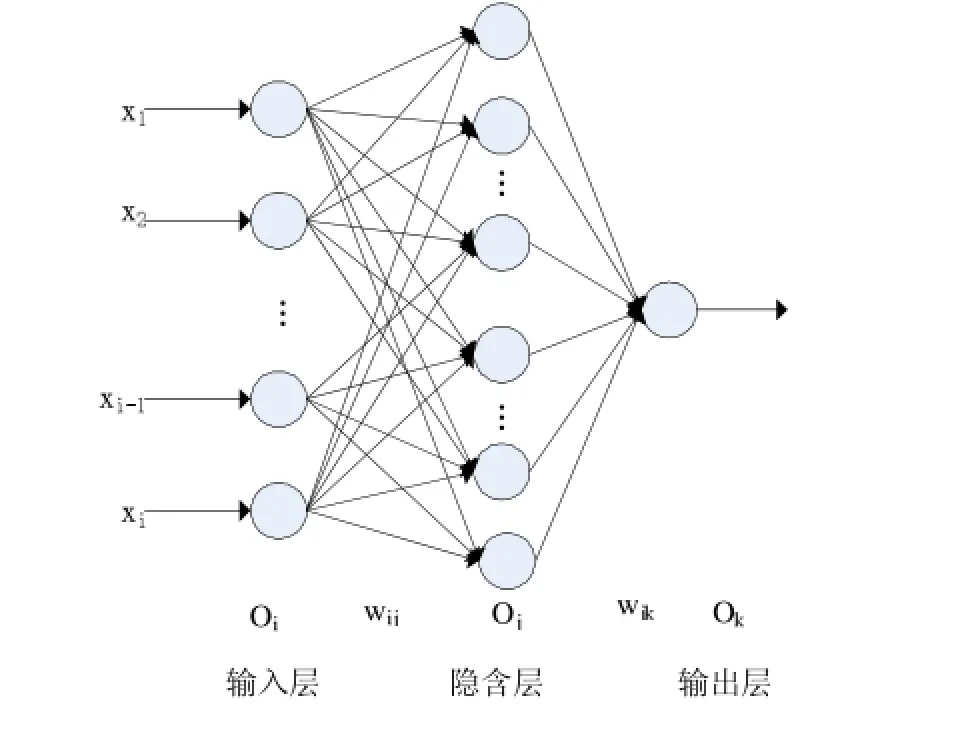
图2 三层前馈式神经网络模型
在BP神经网络中,令I代表输入,O代表输出,对于输入层的神经元i,它它的输入等于输出,即Ii=Oi,对于隐含层的神经元j,则其输入为线性组合,如公式:

其中ωij代表输入层i节点到隐含层j节点之间的权中,兹表示偏置,并且用S型函数做隐含层神经元j激活函数f(x),f'(x)为f(x)的导函数,同时令f(x)即如公式(3)

对于输出层节点,处理方式与隐含层相同,ωij的权重调整公式如下:

其中ωij为更新后的权值,为学习率,0<η<1,对于δj的处理,要从输出节点和非输出节点考虑。
对于输出节点δj表示为:
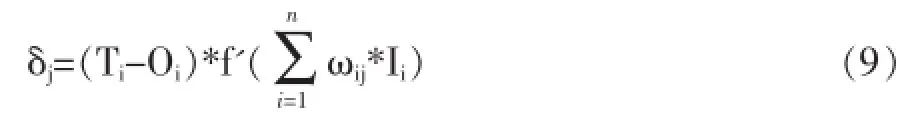
对于非输出型节点δj表示为:
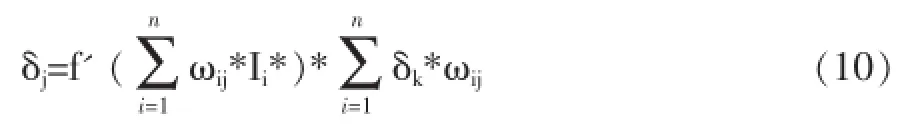
其中Ti和Oi分别表示网络期望输出和实际输出。对于输出节点。迭代到什么时候为止,仅仅当公式(7)达到要求的精度则结束。

4 基于粗集神经网络的信用评价模型构建
在科技金融领域对科技型企业进行信用风险评估过程中,由于每个企业提供的企业信用指标存在多样性和不确定性,因此造成数据指标在收集时也会出现各种缺陷和错误,通过数据整理,其多样性和不确定性主要表现为以下几个方面:一、由于每个企业对于财务指标的定义没有统一,很多企业的财务指标没有统一;二、是由于财务工作人员的原因财务指标数据记录错误;三、由于企业工作人员工作粗心造成该记录的地方空白,记录为空(NULL);对于上述数据,作者对上述数据作了简单的处理,有些进行统一,有些进行了删除,处理之后剩下表1的29个指标,并用{x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29}表示条件属性,具体表示意义如表1。
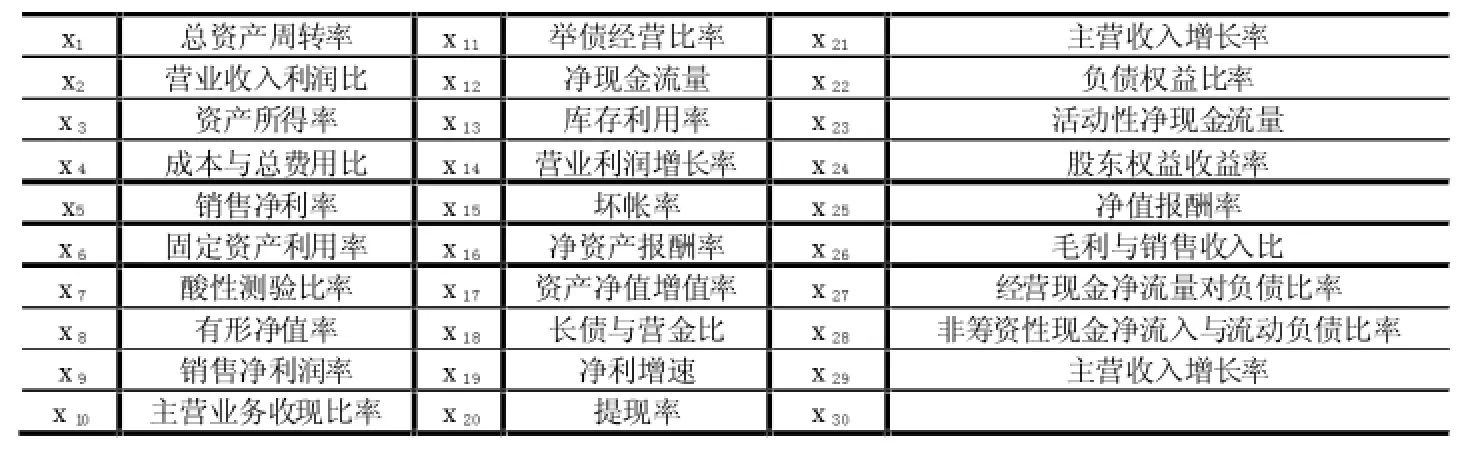
表1 深圳某科技金融机构收集的企业指标
由于上述提供的数据是连续数据,因此必须对上述数据进行离散化处理[9]。将上述指标数据分为5档,为了避免因为有些数据过大或者过小从而导致离散数据失真,本文暂不考虑偏离数据,先将大部分数据离散后再对偏离数据进行处理,因此每个指标有5等份;而对于决策属性D用有信用和无信用来处理,分别用1 和0表示,对文中用到的等区间法可以借鉴王妍提出的处理方法[10]。
(1)条件属性约简
对于知识系统R,令R={x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13,x14,x15,x16,x17,x18,x19,x20,x21,x22,x23,x24,x25,x26,x27,x28,x29,D},因此在知识系统R中,条件属性为C={x1,…x29},值属性为D,条件属性C对论域U的划分 为 C/D={{x1},{x2},{x3},{x4},{x5},{x6},{x7},{x8},{x9},{x10},{x11},{x12},{x13},{x14},{x15},{x16},{x17},{x18},{x19},{x20},{x21},{x22},{x23},{x24},{x25},{x26},{x27},{x28},{x29}},对于信用风险评价模型中对于指标的约简,其思想来源于Pawlak关于重要度的理论,其具体的实现如下:
(1)计算C对D的核CORED(C);
(2)令B=CORED(C),posB(D)=posc(D),接着转(5);
(3)如果∀ci∈C/B.,计算重要度sig(ci,B)=|posB∪{ci}|-|posB(D),同时计算,令B=B∪(Cm);
(4)若posB∪{ci}(D)≠posB(D),转至(3);
(5)若输出B∈REDc(D),则结束。
本文收集了深圳近10年来的40家非上市科技型公司的财务数据,按表1提到的指标整理成知识库,再应用上述约简算法,得到知识库的核为REDc(D)={x1,x9,x13,x15,x18,x20,x22,x24}
表1中的所有指标按照上述步骤进行处理,得到REDc(D={x1,x9,x13,x15,x18,x20,x22,x24}。根据粗糙集的约简理论,要使知识系统保持分类不变情况下,可以认为知识系统依赖于 x1,x9,x13,x15,x18,x20,x22,x246等 8个指标。
(2)应用BP分类
完成上述约简之后,接着应用BP神经网络对知识库进行分类,首先将上述40家公司的8个指标数据进行预处理,将所有的数据映射到[0,1]区间。
本文采用十折交叉验证的方法进行训练,输入神经元为8条,由于是一个二分类问题,因此输出神经元只要1条就可以,本文设置学习率为,η=0.8,学习总误差E(K)≤0.001。具体的训练如下:
(1)初始化神经网络,设置BP中各个节点及各个权值的初始值,文中采用均匀分布随机数,但是要保证BP网络的加权值达到饱和。
(3)将数据集中的数据在网络中训练时,利用公式(2)(3)逐步条件各个权值和节点值。
(4)然后利用公式(5)(6)计算输出节点和非输出节点的误差。
(5)当总误差当总误差E(W)≤0.001则迭代结束,否则进入(3)进行下一迭代。
5 实证分析
为了对本文模型进行有效地验证,本文选取了深圳证券交易所的100个科技型公司的数据作为测试数据集进行验证,其中有20家ST科技型公司和80个非ST科技型公司。为了验证本文模型的有效性,现分别将传统的BP神经网络与基于粗集神经网络应用于同一测试数据集,实验平台采用 Intel Pentium CPU3.2GHz,内存为2GB,OS为Windows XP,以MATLAB 7为仿真软件。实验结果如图3和表2所示,从图3中可以看出,基于粗糙集的BP神经网络在识别率上都优于传统的BP神经网络,且随着测试数据的增加,其识别率也不断提高。
测试时间如下表2所示,从表2可以看出,基于粗糙集的BP神经网络测试所用的时间明显比传统的BP神经网络的测试时间要少,主要原因是因为应用粗糙集约简了知识库的指标,简化了网络,从而减少了训练时间和测试时间。
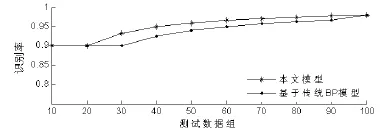
图3 风险控制子系统检测结果图
6 结语
(1)将粗糙集理论与BP神经网络有机结合,构建了基于粗糙集与BP的信用风险评价模型,其中利用粗糙集约简可以在不减少分类能力情况下有效地简化了BP神经网络的复杂度,从而有效地减少了数据采集成本和信用审批成本,有利于科技金融服务工作的迅速开展,更有利于生存创造一定的条件。
(2)实例表明,将本文模型与传统的BP神经网络信用评价模型进行比较,无论在评价的识别率还是评价时间上,本文模型在科学性、合理性及可操作性上都具有一定的优势。
(3)本文在科技金融服务机构如何对企业信用风险进行评价方面做了一次有益的探索,对日后相关课题具有一定的参考价值。

表2 粗集神经网络模型与传统BP神经网络测试时间比较(单位:s)
[1]卢超,钟望舒.提出的商业银行对中小企业信用风险评价的方法探索[J].金融论坛,2009,(9):13-20.
[2]楼际通,楼高文,余锈荣.商业银行个人信用风险评价的投影寻踪建模及其实证研究[J].经济数学,2013,30(4):26-32.
[3]曾诗鸿,王芳.基于KMV模型的制造业上市公司信用风险评价研究[J].预测,2013,32(2):61-64.
[4]朱天星,于立新,田慧勇.商业银行个人信用风险评价模型研究[J].问题探讨,
[5]郭志军,何昕,魏仲慧.一种基于粗糙集神经网络的分类算法[J].计算机应用研究,2011,28(3):838-850.
[6]王国胤,姚一豫,于洪.粗糙集理论与应用研究综述[J].计算机学报,2009,32(7):1229-1246.
[7]张建华.知识管理中的知识进化绩效评价机制研究[J].科学学与科学技术管理2013,34(7):28-36.
[8]张卉.基于粒子群优化BP神经网络的房价预测[J].价值工程,2012(5):207~208.
[9]于锟,刘知贵,黄正良.粗糙集理论应用中的离散化方法综述[J],2005,20(4):32-36.
[10]王妍,潘瑜春,王惠.基于Voronoi和信息滴的空间群样点检测[J].计算机工程与设计,2010,31(18).:45-49.
WANG Jie1,CHEN Gang2
(1.Dongguan Electronic Computing Center,Dongguan 523123;2.Department of Computer Technology,Guangdong Polytechnic Institute,Zhongsan 528458)
Now the current credit approval has low efficiency and cost too much,the reasons for that is bad enterprise credit evaluation model,too much evaluation index and too long evaluation time;To solve this problem,proposes a new credit evaluation model based on rough sets and BP,the model effectively reduces financial indicators of enterprises without affecting the classification attributes,at the same time,uses BP neural network fault tolerant ability,well classified the credit businesses.At last,puts this model to application,the results show that the model is effective.
Technology Finance;Risk Evaluation;Rough Set;Neural Network
国家创新基金(No.13C26214404497)、国家自然科学基金项目(No.61175027)
1007-1423(2016)21-0003-06
10.3969/j.issn.1007-1423.2016.21.001
王洁(1962-),女,广东增城人,副研究员,博士研究生,研究方向为科技管理与服务
陈刚(1977-),男,江西高安人,博士研究生,副教授,研究方向为人工智能、数据挖掘
2016-05-16
2016-07-11Research on Credit Risk Evaluation System Based on Rough Set and BP
