应力比对钢纤维高强混凝土梁疲劳寿命影响的试验研究

李书群,姬宏奎,杨　松

(河北省水利水电第二勘测设计研究院， 河北 石家庄 050021)



应力比对钢纤维高强混凝土梁疲劳寿命影响的试验研究

李书群,姬宏奎,杨松

(河北省水利水电第二勘测设计研究院， 河北 石家庄 050021)

通过对钢纤维钢筋高强混凝土梁不同应力比的弯曲疲劳荷载试验，研究了试件的疲劳寿命及疲劳强度。根据不同应力比作用下梁试件的疲劳寿命N，得出本次试件梁的S-N曲线，裂缝开展规律。应用Miner理论和科尔顿-多兰(Corten-Dolan)公式进行疲劳损伤计算、疲劳寿命分析及预测，最后采用断裂力学理论分析裂缝开展规律以预测疲劳寿命,并提出裂缝开展宽度计算公式。

应力比；疲劳寿命；Miner理论；S-N曲线；钢纤维；高强混凝土

目前承受疲劳荷载的混凝土构件已得到广泛的应用[1-3]以及研究，主要研究成果表明应力水平、应力幅值、配筋等对混凝土构件疲劳性能有显著影响。钢纤维混凝土梁的抗折、断裂性能、弯曲韧性以及部分掺加钢纤维混凝土梁的疲劳性能也已有研究[4-8],文献[9]对钢纤维混凝土性能进行数值模拟分析。本文通过对梁试件进行不同应力幅值作用下的疲劳循环荷载试验，根据不同的理论模型对钢纤维高强混凝土疲劳寿命进行分析及计算，并提出相关公式。

1　试验概况

试验采用P.O 42.5水泥；碎石，粒径10 mm～25 mm，连续级配；中砂，细度模数2.70；钢纤维采用Dramix水溶性钢纤维，型号RC-65/35-BN，抗拉强度1 345 MPa，长度为35 mm，直径为0.55 mm，长径比为64。试验配合比见表1。

表1　混凝土配合比

本试验共制作了4组尺寸和配筋相同的矩形截面简支梁，梁截面尺寸均为150 mm×300 mm，钢纤维体积率均为1%，配筋如图1所示，编号为L1、L2、L3、L4。

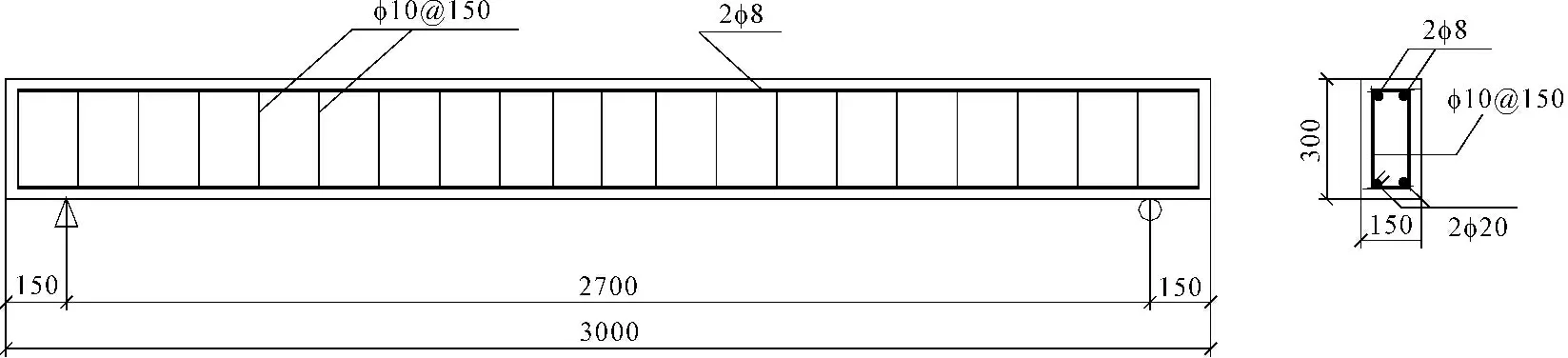
图1试验梁尺寸及配筋图

试验采用单点集中力加载方案，荷载由50 t疲劳试验机液压千斤顶作用在梁跨中位置，施加脉动荷载。疲劳荷载上限根据文献[10-12]计算的极限承载力Mu确定，分别为fL1=0.7Mu、fL2=0.6Mu、fL3=0.5Mu、fL4=0.4Mu，疲劳荷载下限均为0.15Mu。由此可得梁的应力比为ρL1=0.214、ρL2=0.25、ρL3=0.3、ρL4=0.375。疲劳荷载的加载采用等幅加载方式，频率为5 Hz。先进行一次静载试验，当荷载循环次数分别达到规定等级(一级1万次，二级5万次，三级10万次、四级20万次、五级50万次、六级100万次、七级200万次)时，进行一次静载试验，分级静力加载至疲劳荷载上限，目的是观测试件梁的应力应变关系变化过程，以及裂缝宽度与疲劳循环次数的关系，用于理论分析计算。试验过程中若荷载循环次数达到n级仍未破坏则此前的荷载循环每达到一级时均进行一次静载试验。若循环次数达到七级仍未破坏则进行静力加载直至破坏，记录破坏荷载，每次静载试验做好试验数据记录及整理。

2　结果分析

2.1疲劳破坏特征

本次试验钢纤维高强混凝土梁的疲劳寿命及破坏情况见表2。

表2　疲劳试验破坏特征

从表2中可以看出，应力比对构件的疲劳破坏形态影响显著。试件梁L1 、L2、 L3均在循环次数未到七级时发生了疲劳破坏，只有试件梁L4应力比最大经过七级荷载循环次数未破坏。由此可见，钢纤维高强混凝土梁疲劳寿命随着应力比的增大而增大。部分构件破坏形态见图2和图3。

图2　裂缝达到限值

图3钢筋疲劳断裂

2.2疲劳曲线(S-N曲线)

抗疲劳破坏特性分析主要由经验规律[13]来进行，目前应用最广泛的是S-N曲线。疲劳曲线是指在疲劳循环荷载作用下，应力比(应力水平、应力幅值)和疲劳寿命之间的关系曲线。本文采用应力幅值S和疲劳寿命N绘制S-N曲线[14]。

以4根试件梁的疲劳荷载幅值S为纵坐标，疲劳破坏时的荷载循环次数N为横坐标，作图即得本次试验试件梁的Wholer图，见图4。

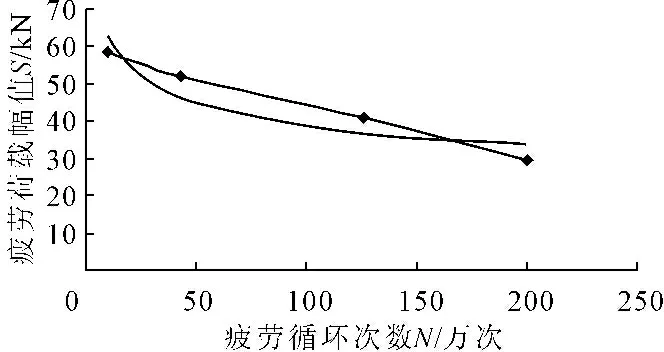
图4疲劳试验梁S-N曲线

对上图S-N曲线进行拟合即得疲劳荷载幅值和循环次数之间的关系式(相关系数为0.988)：

S=101.97N-0.2092

(1)

转换为对数公式形式：

lgN=9.598-4.78lgS

(2)

根据以上两式可以由循环次数推求钢筋钢纤维高强混凝土梁的疲劳极限荷载，也可以由梁的荷载推求疲劳寿命。根据本次试验循环次数达到七级时(N=200)可得S=33.65 kN，为静载试验极限荷载Mu=116 kN的29%。

2.3基于Miner法则的钢纤维高强混凝土梁疲劳损伤分析

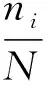
结果表明D值除L4外均大于1，用来预估计算构件的疲劳寿命，安全系数较高但尚不够经济合理。从机理上分析认为，钢筋钢纤维混凝土构件抗疲劳性能分为混凝土开裂前阶段、混凝土开裂后钢纤维开裂前阶段、钢纤维开裂后钢筋断裂前阶段，各个阶段吸收能量的能力不同，损伤不再呈单一的直线线性累积。此外，普通混凝土开裂后即退出工作，但是钢纤维混凝土开裂后裂缝之间的钢纤维仍能承受荷载吸收能量，而且裂缝两侧的混凝土内的钢纤维也和裂缝处未断裂的钢纤维共同受力(裂缝两侧钢纤维带动裂缝两侧的混凝土参与受力)，相对普通混凝土这就大大延缓了裂缝的开展，直到裂缝处钢纤维疲劳断裂后混凝土和钢纤维全部退出工作，裂缝继续开展，由于两种材料吸收能量的能力不同，累积损伤也就不再是线性累加而是呈现不规则折线形。

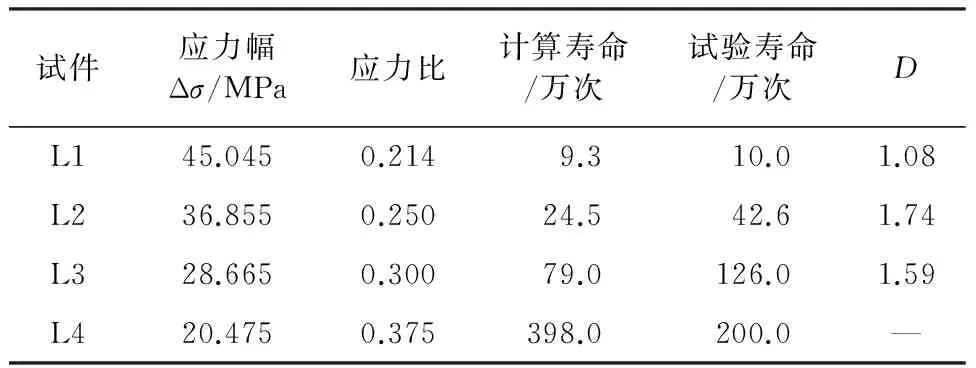
表3　试验结果、Miner理论计算结果及D值

注：L4在荷载循环200万次时没有破坏，未计算D。

2.4基于修正的线性累积损伤理论的钢纤维高强混凝土梁疲劳损伤分析

由表3可知，D值都大于1，正如上述分析因为损伤累计不再是线性的，不同阶段不同的材料吸收能量的能力是不同的，直接采用Miner理论进行疲劳寿命分析计算是不够准确的，因此需要一个系数加以修正。科尔顿-多兰(Corten-Dolan)理论的计算方法及公式形式和本试验相近且应用较广，其公式为：

(3)

对公式整理可得：

(4)

式(4)对数形式：

(5)

其中：σI为梁试件最大应力，NI对应于σI疲劳寿命，d为材料常数，由试验结果拟合得出。

由式(5)可以看出，应力对数与疲劳寿命对数成线性关系，试验材料常数d即为该直线的斜率，材料常数d考虑了不同阶段不同的材料(混凝土、钢纤维、钢筋)吸收能量的能力，是一个综合高强钢纤维钢筋混凝土抗疲劳性能的一个参数。根据试验结果拟合出钢纤维高强混凝土梁的材料常数d=7.6。采用式(5)估算钢纤维高强混凝土梁的疲劳寿命结果见表4。

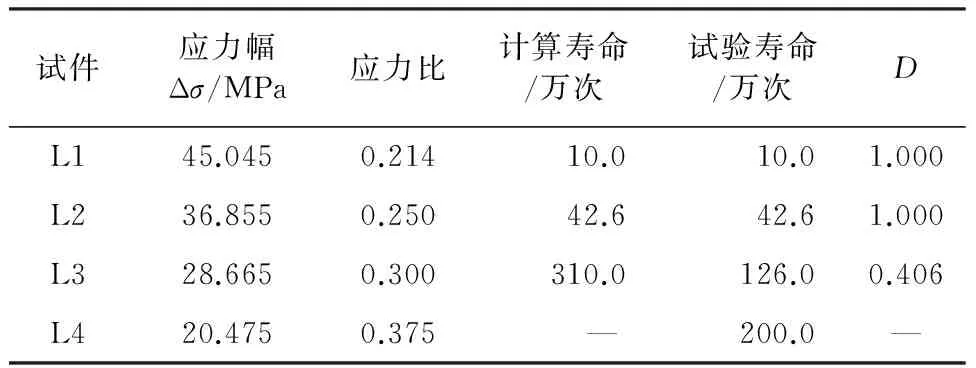
表4　修正线性累计损伤理论计算结果

注：因L4循环至200万次没有发生破坏，所为未计算D；梁试件L3两根钢筋只有一根断裂仍有继续承受疲劳荷载的能力，本次试验断裂一根钢筋即停止试验，因此计算D值偏小。

根据表4计算结果可知，采用修正的线性累积理论计算钢纤维高强混凝土梁的疲劳损伤度D更接近于梁的疲劳寿命，即D更接近于1。采用修正的线性损伤累积公式计算试件疲劳寿命考虑了梁试件中混凝土、钢纤维及钢筋不同材料吸收疲劳荷载能量的能力不同，采用一个参数进行修正，拟合不同材料的共同作用，得出试验材料常数d，弥补了Miner公式在高强钢纤维混凝土疲劳寿命预测中的不足。

2.5断裂力学理论分析疲劳寿命

在结构构件疲劳设计和寿命分析中断裂力学方法已经或正在得到应用。从试验记录看，梁试件均在第一次静载试验时已出现较多裂缝，初始裂缝主要集中在跨中集中力作用位置区域，而后逐渐向两侧发展，10万次循环后裂缝数量增加及发展程度就不太明显。裂缝开展宽度随循环次数规律图见图5。

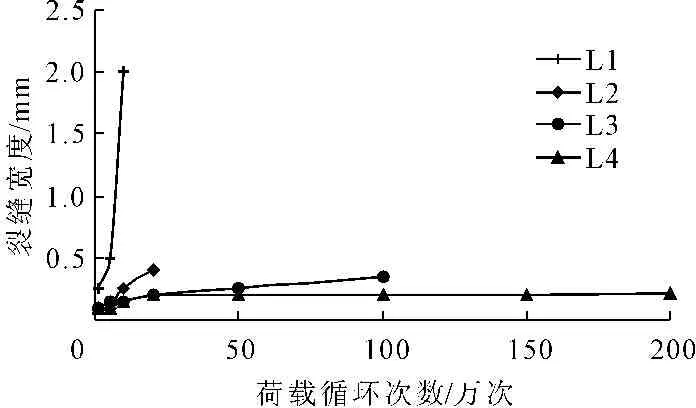
图5裂缝最大宽度随循环次数变化规律

疲劳裂纹扩展理论是研究构件的裂纹扩展的理论[16]。目前应用较为普遍的有Parris公式和Irring公式。本文采用Parris公式：

(6)

式中：a为裂缝宽度，则da/dN为疲劳裂纹扩展速率；Δk=kmax-kmin，在本文为应力幅值；c和m均为试验拟合常数。

对Parris定积分，即

(7)

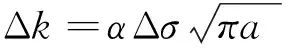
将Δk代入式(3)～式(6)得：

(8)

(9)

经计算分析建议以构件静载极限强度的1/2即0.5σ为分界点，当σmax≤0.5σ时c1=2×10-6,m=2.45；σmax>0.5σ时c1=7.55×10-6,m=2.45即：

(10)

图5中裂缝的开展速率曲线的斜率经拟合后即为其裂缝开展速率，由公式(10)根据裂缝开展宽度即可计算出该宽度值下疲劳循环寿命N。由表5可知采用本文公式计算，计算值与实测值基本吻合。

表5　疲劳寿命计算值与实测值

3　结　论

应力比对钢纤维高强混凝土梁的破坏形态、疲劳寿命影响显著，随着应力比的减小疲劳寿命显著减小，裂缝开展速率随应力比的减小增幅显著。本文采用疲劳损伤线性累积理论计算，结果表明修正的线性累积理论科尔顿-多兰公式较Miner理论能更好的预测疲劳损伤度；采用断裂力学公式(Parris)由裂缝宽度开展速率预测疲劳寿命须采用分级公式。

[1]曹康建.湿喷钢纤维混凝土在隧道单层衬砌中的应用[J].水利与建筑工程学报,2011，9(3)：83-102.

[2]郭辉.钢纤维混凝土在拱桥桥面加固中的应用[J].价值工程，2011,30(22)：106.

[3]王元耀.钢纤维混凝土在小杞水电站中的应用[J].水利天地，2013(7)：38-40.

[4]付操,宋海清.低温钢纤维混凝土梁抗折疲劳特性的试验研究.混凝土与水泥制品[J].混凝土与水泥制品，2012(4)：40-43.

[5]高丹盈,赵亮平,冯虎，等.钢纤维混凝土弯曲韧性及其评价方法[J].建筑材料学报，2014，17(5):783-789.

[6]窦利萍，李风兰，谢继义.钢筋钢纤维混凝土梁正截面抗裂计算方法[J].华北水利水电学院学报，2002，23(2)：35-38.

[7]黄煜镔,钱觉时,王智，等.钢纤维混凝土断裂性能研究[J].建筑技术，2002,33(1)：28-29.

[8]张明,高丹盈,赵军.钢纤维部分增强高强混凝土梁疲劳性能的试验研究[J].华北水利水电学院学报，2012，33(6)：56-58.

[9]宋艳，朱珍德，张慧慧.深埋隧道喷射钢纤维混凝土支护的数值模拟[J].水利与建筑工程学报,2013，11(2):204-208.

[10]中国建设标准化协会.纤维混凝土结构技术规程：CECS 38:2004[S].北京：中国计划出版社，2004.

[11]高丹盈，赵军，朱海堂.钢纤维混凝土设计与应用[M]．北京：中国建筑工业出版社，2002．

[12]赵国藩，彭少民，黄承逵.钢纤维混凝土结构[M]．北京：中国建筑工业出版社，1999．

[13]张小辉.钢纤维混凝土弯曲疲劳及其损伤特性和细观强度研究[D].昆明：昆明理工大学，2001.

[14]曾春华，邹十践(编译).疲劳分析方法及应用[M].北京:国防工业出版社，1991.

[15]李宇.螺栓球节点网架用40Cr高强螺栓的疲劳破坏机理及寿命估算[D].太原：太原理工大学，2003.

[16]Suresh S.材料的疲劳[M].王中光等译.北京:国防工业出版社，1995.

Experimental Study of Stress Ratio to Fatigue Life of Steel Fiber Reinforced High-Strength Concrete Beams

LI Shuqun, JI Hongkui, YANG Song

(TheSecondInstituteforDesignandResearchofWaterConservancyandHydropowerofHebeiProvince,Shijiazhuang,Hebei050021,China)

Through the fatigue tests of steel fiber reinforced high strength concrete beams, the impacts to the fatigue strength and fatigue life caused by the stress ratio was analized. Based on the fatigue life N under different stress ratios，this paper acquired the S-N curve of the beams. Miner theory and Colton-Dolan formula were used for fatigue damage calculation, fatigue life analysis and prediction. Additionally the crack expanding law was carried out by the theory of fracture mechanics in order to predict the fatigue life and propose the crack width calculation formula.

stress ratio; fatigue life; Miner theory; S-N curve; steel fiber; high strength concrete

10.3969/j.issn.1672-1144.2016.04.031

2016-03-02

2016-04-03

李书群(1973—)，男，河北邢台人，高级工程师，主要从事水利工程结构设计和研究工作。E-mail:hbshuqunli@163.com

TU375.1

A

1672—1144(2016)04—0157—04